MULTICRITERIA DECISION MAKING

IN BALANCED MODEL OF FUZZY SETS

Wladyslaw Homenda

Faculty of Mathematics and Information Science

Warsaw University of Technology, pl. Politechniki 1, 00-661 Warsaw, Poland

Keywords:

Decision making, fuzzy sets, balanced fuzzy sets, negative information.

Abstract:

In the paper aspects of negative information and of information symmetry in context of uncertain information

processing is considered. Both aspects are presented in frames of fuzzy sets theory involved in data aggrega-

tion and decision making process. Asymmetry of classical fuzziness and its orientation to positive information

are pointed out. The direct dependence of symmetry of uncertain information on negative information mainte-

nance is indicated. The symmetrical, so called balanced, extension of classical fuzzy sets integrating positive

and negative information an paralleling positiveness/negativeness with symmetry of fuzziness is presented.

Balanced counterparts of classical fuzzy connectives are introduced.

1 INTRODUCTION

In the paper a discussion on aspects of negative infor-

mation and information symmetry is presented. The

discussion is based on an observation of asymmetry

of operators in classical theories of uncertain infor-

mation and in theories with focus turned on fuzzy

sets. Preliminary discussion on asymmetry of clas-

sical fuzzy sets is presented in Section 2. It shows

an inclination of classical fuzzy connectives to posi-

tive information and incompatibility with negative in-

formation. Issues related to negative information are

outlined in Section 3. Assumed symmetry of negative

and positive information integrates both types of in-

formation. The integrated approach to parallelism of

negativeness/positiveness and symmetry of informa-

tion is introduced in Section 4. The integration of neg-

ativeness and symmetry is inherently drawn in an idea

of so called balanced extension of fuzzy sets. This

idea was introduced in (Homenda, 2001) and then

discussed in several papers (Homenda, 2004; Home-

nda, 2003; Homenda and Pedrycz, 2002). Finally, an

application of the classical approach to uncertainty

versus its balanced model is compared in the exam-

ple 4.1. The example outlines importance of negative

information in decision making process in real envi-

ronment.

2 ASYMMETRY OF FUZZY SETS

Fuzzy set theory is often used to partition a universe

into two subsets if partition criteria are not crisp. If

partition criterion is uncertain, deﬁnition of subsets as

fuzzy sets over the universe is a natural way to model

uncertainty. However, neither crisp, nor fuzzy mod-

elling avoids problems with law of excluded middle.

Partitioning the universe into two complementary

sets suggests comparable signiﬁcance of both sets un-

less additional principle is given. In such partition-

ing elements of the universe can be classiﬁed as true

and false, like and dislike, good and bad, etc. with-

out any emotional evaluation of these terms. We will

simply talk about positive and negative information,

again - without emotional evaluation of both terms.

Using several criteria in partitioning we may classify

elements of the universe with regard to every criterion

separately. Having a number of pairs of complemen-

tary sets it is necessary to aggregate these results in

order to get ﬁnal two sets separation of the universe.

Using classical aggregators we can choose between

all good criteria or one good criterion. The ﬁrst one,

where the elements classiﬁed as good one must have

all criteria good, is implemented by conjunction. The

second one, where the element classiﬁed as good can

have only one good criterion, is implemented by dis-

Homenda W. (2007).

MULTICRITERIA DECISION MAKING IN BALANCED MODEL OF FUZZY SETS.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 40-46

 SciTePress

junction. Both aggregation connectives, conjunction

and disjunction, raise clear asymmetry under comple-

ment. If elements of one set are classiﬁed as having

all criteria good, elements of the complementary set

must have at least one criterion bad instead of ex-

pected the same condition of all criteria bad. Keep-

ing the same condition (either all criteria, or at least

one criterion) in deﬁnition of both sets raises troubles

with law of excluded middle mentioned above. Fol-

lowing this way of thinking we need other connec-

tives that will balance aggregation of decisions based

on singular criterion. The above discussion leads to

the conclusion that classical fuzzy set theory is asym-

metrical with regard to processing opposite values of

given attributes.

2.1 Symmetrization of the Scale

A classical fuzzy set A in the universe X can be de-

ﬁned in terms of its membership function µ : X →

[0,1], where the value 0 means exclusion of the el-

ement from the set while the values greater than 0 ex-

press the grade of inclusion of the element into the

set. However, membership function does not deﬁne a

grade of exclusion, the grade of negative information.

Therefore, fuzzy sets theory distinguishes grades of

inclusion and reserves only one value - 0 - for exclu-

sion. This raises asymmetry of this interpretation.

Membership function deﬁnes fuzzy connectives:

union, intersection and complement. The deﬁnitions

are expressed by max, min and complement to 1, i.e.

d(x,y) = max{x,y}, c(x,y) = min{x,y} and n(x) =

1− x. Classical connectives are asymmetrical. Union

gets its value from the greater argument, despite of

the values of both arguments. Similarly, intersection

gets its value from the smallers argument only.

We can split values of a given criterion in the spirit

of good and bad allocating the values of the interval

[0,0.5) as pieces of negative information relevant to

bad values and the values of the interval (0.5.1] as

pieces of positive information relevant to good val-

ues. The value 0.5, the center of the unit interval

[0,1], is a numerical representation of the state of no

negative/positive information. Being compatible with

common meaning of membership function let us as-

sume that the greater the value of positive informa-

tion, the stronger the good value of the criterion. By

symmetry, the smaller the value of negative informa-

tion, the stronger the bad value of the criterion.

This interpretation is well-matched with the com-

mon sense of ordering of the negative/positive values.

The ordering could be seen as monotonicity of nega-

tive/positive information mapping: it starts from the

left end of the unit interval representing strong nega-

tive information, then goes toward middle of the unit

interval diminishing strength of negative information,

then crosses the middle point of the unit interval and

then goes towards the right end of the unit interval

increasing strength of positive information.

This interpretation is also well-matched with the

common sense of symmetry of the negative/positive

values with the symmetry center in the value 0.5. The

linear transformation f(x) = 2x − 1 of the unit inter-

val [0,1] into the symmetrical interval [−1,1] points

out the symmetry. In this transformation negative in-

formation is mapped to the interval [−1,0), positive

information - to the interval (0, 1] and the state of no

information - to the value 0.

2.2 Connectives Asymmetry

The classical fuzzy connectives stay asymmetrical

even with the symmetrical bipolar scale of the inter-

val [−1,1] applied. Both classical fuzzy connectives

get their values from the maximal argument (union,

maximum) and the minimal argument (intersection,

minimum). Classical fuzzy connectives were gen-

eralized to triangular norms: maximum is an exam-

ple of t-conorms, minimum is an example of t-norm,

c.f. (Schweizer and Sklar, 1983). Strong t-norms

and t-conorms, the special cases of triangular norms,

have an interesting property: if both arguments are

greater than 0 and smaller than 1, the result of strong

t-conorm exceeds the greater argument while the re-

sult of strong t-norm is less than smaller argument,

c.f. (Klement et al., 2000). This property might be in-

terpreted that union tends to positive information de-

spite of the values of its arguments while intersection

tends to negative information despite of the values of

its arguments. In other words, symmetrical interpre-

tation of the unipolar scale makes that strong t-norm

increases certainty of negative information and de-

creases certainty of positive information. And vice

versa, strong t-conorm decreases certainty of negative

information and increases certainty of positive infor-

mation. This observation emphasizes the asymmetry

of fuzzy connectives, c.f. Figure 1.

The problem of asymmetry of fuzzy connec-

tives was discussed in number of papers, e.g. (De-

tyniecki and Bouchon-Meunier, 2000b; Homenda and

Pedrycz, 1991; Homenda and Pedrycz, 2002; Silvert,

1979; Yager, 1988; Yager, 1993; Zhang W. R., 1989).

In these papers discussion on asymmetry of fuzzy sets

and uncertain information processing was undertaken

for different reasons, though common conclusions led

to importance of the symmetry problem in fuzziness

and uncertainty.

Figure 1: Asymmetry of classical triangular norms.

3 NEGATIVE INFORMATION

The mapping of negative and positive information in

the scale of unit interval [0, 1] as well as in the sym-

metrical interval [−1,1] bring incompatibility with

connectives, so the question is raised if negative in-

formation can be considered as a subject of uncer-

tainty. The question seems justiﬁed since negative in-

formation is hardly interpretable in classical set the-

ory and classical fuzzy sets theory. However, nega-

tive information, as explained in the introductory re-

marks to this section, play important role in different

ﬁelds. From psychological studies it is known that

human beings convey symmetry in their behavior, c.f.

(Grabisch M., 2002). One can be faced with positive

(gain, satisfaction, etc.) or negative (loss, dissatisfac-

tion, etc.) quantities, but also with a kind of disin-

terest (does not matter, not interested in, etc.). For

instance, one either likes to listen to the music while

reading an interesting novel or does not like to listen

to the music then or even music is only a background

not affecting him at all. These quantities could be in-

terpreted in context of positive/negative/neutral infor-

mation. On the other hand, in economy psychologi-

cal attempt to decision making process with uncertain

premises overheads traditional models of customers

behavior. The pseudocertainty effect is a concept

from prospect theory. It refers to people’s tendency

to make risk-averse choices if the expected outcome

is positive, but risk-seeking choices to avoid nega-

tive outcomes. Their choices can be affected by sim-

ply reframing the descriptions of the outcomes with-

out changing the actual utility, c.f. (Kahneman and

Tversky, 2004). Aggregation of positive and negative

premises leads to implementation of a crisp decision.

Modelling of such an attempt requires processing of

positive/neutral/negative information.

An interesting contribution to positive/negative in-

formation maintaining could be found in the theory of

intuitionistic fuzzy sets (Atanassov, 1986) and in very

similar theory of vague sets (Gau and Buehrer, 1993).

Another approach to positive/negative information is

discussed in twofold fuzzy sets, c.f. (Dubois and

Prade, 1983). In these theories, uncertain informa-

tion is represented as a pair of positive/negative com-

ponents numerically described by membership values

from the unit interval [0,1]. Both components are tied

with degree of indeterminacy which stays that sum

of membership values of both components cannot ex-

ceed the value 1. However, no tool to combine both

components is provided in these theories. Since infor-

mation aggregation leading to non ambiguous result is

a clue issue in decision making process, these theories

must be supported by information aggregators in such

a process.

The very early medical expert system MYCIN,

c.f. (Buchanan and Shortliffe, 1984), combine posi-

tive and negative information by somewhat ad hock

invented aggregation operator. In (Detyniecki, 2000)

it was shown that MYCIN aggregation operator is

a particular case in a formal study on aggregation

of truth and falsity values, c.f. (Detyniecki and

Bouchon-Meunier, 2000a) for further discussion on

aggregation of positive and negative information.

Having many premisses, usually uncertain, we

need to produce nonambiguous information that

yields a unique decision. Therefore aggregation of in-

formation is crucial in decision making process. The

topic of information aggregating has been studied in

number of papers. An interesting considerations on

information aggregation could be found in - for in-

stance - (Calvo T., 2001; Detyniecki and Bouchon-

Meunier, 2000a; Silvert, 1979; Ovchinnikov, 1998;

Yager and Rybalov, 1998; Yager and Rybalov, 1996;

Zhang W. R., 1989).

4 SYMMETRIZING FUZZINESS

Fuzzy connectives stay asymmetrical with sym-

metrized scale. The incompatibility of symmetrical

interpretation of the scale and asymmetrical behav-

ior of fuzzy connectives suggest incorrectness of scale

symmetrization. This discussion leads to the hypoth-

esis that Zadeh’s extension of crisp sets to fuzzy sets,

c.f. (Zadeh, 1965), relied on dispersion of positive in-

formation of the crisp point {1} into the interval (0,1].

However, negative information of the point {0} was

still bunched in this point, c.f. Figure 2. This hy-

pothesis can be supported by similarity of balanced

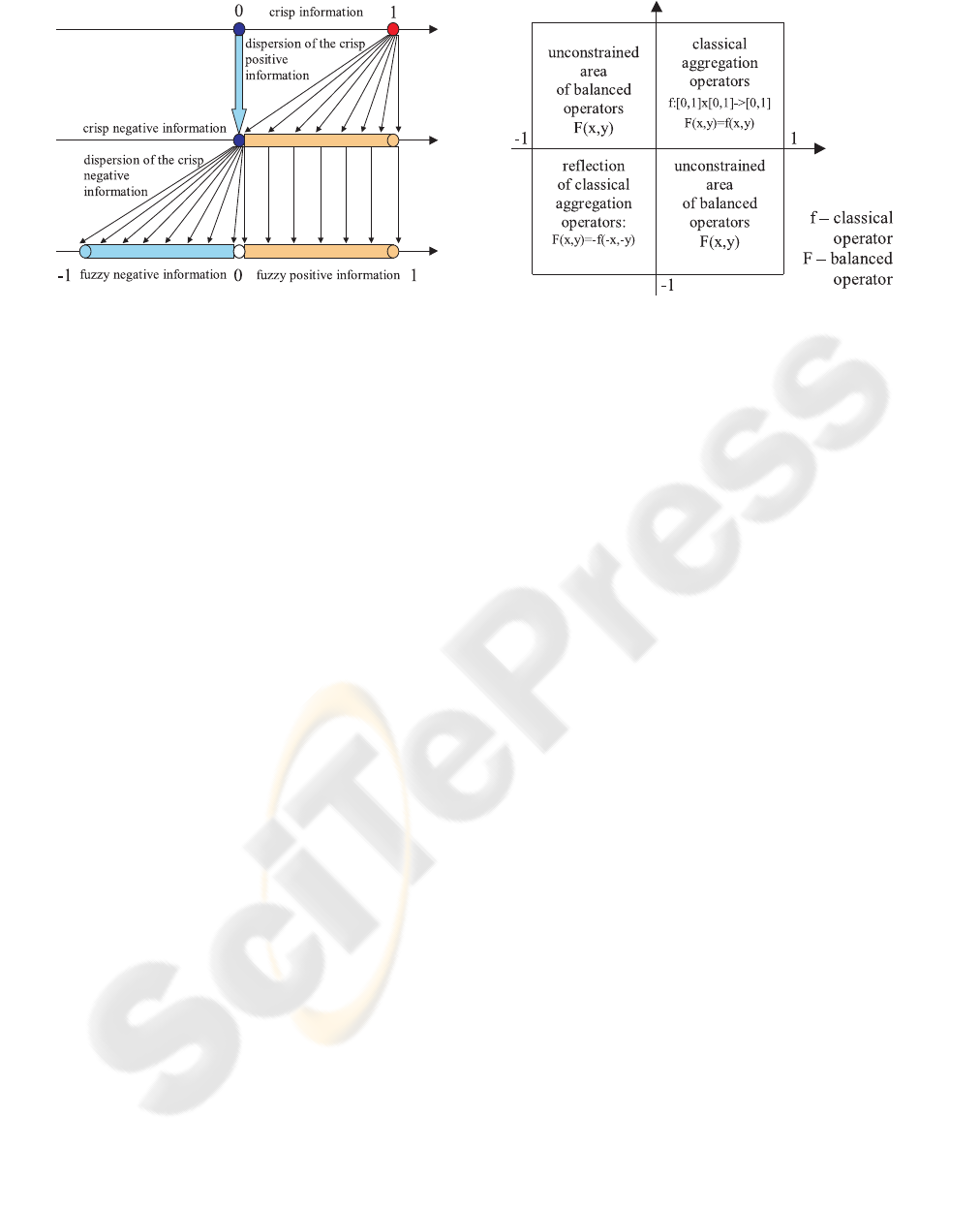
Figure 2: Extension of fuzzy sets to balanced fuzzy sets.

triangular norms and uninorms and nullnorms - the

products of different approaches to fuzzy connectives

extension, c.f. (Homenda, 2003)

4.1 Balanced Symmetrization of the

Scale

Now, the process of information dispersion is applied

again to information concentrated in the point {0}.

This operation extends classical fuzzy sets to bal-

anced fuzzy sets, c.f. (Homenda, 2004; Homenda,

2003). The extension is being done by dispersion

of crisp negative information bunched in the point

{0} into the interval [−1.0) without affecting clas-

sical fuzzy sets based on the unit interval [0,1] c.f.

Figure 2. Thus, classical fuzzy sets will be immersed

in a new space of balanced fuzzy sets. Since both

types of information - positive and negative - are as-

sumed to be equally important, it would be reasonable

to expect that such an extension will provide a kind of

symmetry of positive/negative information.

Concluding, the following symmetry principle can

be formulated: the extension of fuzzy sets to balanced

fuzzy sets relies on spreading negative information

(information about exclusion) that ﬁt the crisp point

{0} of fuzzy set into the interval [−1, 0). The ex-

tension will preserve properties of classical operators

for positive information. It will provide the symme-

try of positive/negative information with the center of

symmetry placed in the point 0, c.f. Figure 2. It is

worth to underline that this operation is entirely dif-

ferent than simple linear rescaling of the unit inter-

val [0,1] into the interval [−1,1]. The linear function

f(x) = 2x− 1 is replaced by the transformation that is

not a function: it allocates the whole interval [−1,0)

as a ”value” in the point 0.

Figure 3: Balanced extension of fuzzy operators.

4.2 Symmetry of Balanced Connectives

Triangular norms generalize the concept of set op-

erations: union and intersection, c.f. (Schweizer

and Sklar, 1983). Triangular norms, t-norms and t-

conorms, together with negation, the basic fuzzy con-

nectives are the subject of the discussion of connec-

tives symmetrization.

Deﬁnition 4.1 Triangular norms: t-norm t and t-

conorm s, are mappings t : [0,1] × [0,1] → [0, 1] and

s : [0, 1] × [0,1] → [0,1] satisfying the following ax-

ioms:

1. t(a,t(b,c)) = t(t(a,b),c)

s(a,s(b,c)) = s(s(a, b), c) associativity

2. t(a,b) = t(b, a)

s(a,b) = s(b, a) commutativity

3. t(a,b) ≤ t(c, d) if a ≤ c & b ≤ d

s(a,b) ≤ s(c, d) if a ≤ c & b ≤ d monotonicity

4. t(1,a) = a for a ∈ [0,1] boundary

s(0,a) = a for a ∈ [0,1] conditions

t-norms and t-conorms are dual operations in the

sense that for any given t-norm t and given negation

operator assumed here to be complement to one, we

have the dual t-conorm s deﬁned by the De Morgan

formula s(a,b) = 1−t(1− a,1− b). And vice-versa,

for any given t-conorm s, we have the dual t-norm t

deﬁned by the De Morgan formula t(a,b) = 1−s(1−

a,1− b). Duality of triangular norms causes duality

of their properties. Note that the max/min is a pair of

dual t-norm and t-conorm.

The idea of balanced extension of classical fuzzy

connectives must be compatible with the concept of

balanced extension of the unipolar scale and with the

symmetry principle formulated in Section 4.1. This

requirements and symmetry of the balanced fuzzy

scale of the interval [−1,1] determines the domain of

symmetrized balanced connectives to be the square

[−1,1] × [−1,1]. Preservation of classical fuzzy sets

properties requires preservation of properties of clas-

sical fuzzy connectives on the unit square [0,1] ×

[0,1]. Conversely, expected symmetry of positive and

negative information puts strict restrictions on bal-

anced extension on the square [−1,0] × [−1,0]. The

same factors determine the co-domain of symmetrical

fuzzy connectives to the interval [−1,1]. This idea of

the balanced extension of classical fuzzy connectives

is outlined in Figure 3. It is clear that balanced con-

nectives are simple reﬂection of respective classical

connectives on the square [−1,0] × [−1,0]. The re-

maining parts of the domain of balanced connectives

are not explicitly constrained. However, some con-

strains will be put when other properties of connec-

tives are considered. These properties come from nat-

ural extension of the axioms of the triangular norms

deﬁnition onto the whole domain of balanced opera-

tors.

This discussion leads to the deﬁnition of balanced

negation, balanced t-norms and balanced t-conorms.

Deﬁnition 4.2 of balanced connectives.

The mapping N : [−1,1] → [−1, 1], N(x) = −x is the

balanced negation.

The mappings T : [−1,1] × [−1,1] → [−1,1] and

S : [−1, 1] × [−1, 1] → [−1,1] are balanced t-norm

and balanced t-conorm, respectively, assuming that

they satisfy the following axioms in the whole domain

[−1,1] × [−1,1] unless deﬁned explicitly:

1., 2., 3.

associativity, commutativity and monotonicity

4. T(1, a) = a for a ∈ [0, 1] boundary

S(0,a) = a for a ∈ [0,1] conditions

5. T(x, y) = N(T(N(x), N(y)))

S(x,y) = N(S(N(x),N(y))) symmetry

Conclusion 4.1 The deﬁnitions of balanced t-norm

and balanced t-conorm restricted to the unit square

[0,1] × [0,1] are equivalent to the classical t-norm

and classical t-conorm, respectively.

Conclusion 4.2 Balanced t-norm and balanced t-

conorm restricted to the square [−1, 0] × [−1, 0] are

isomorphic with the classical t-conorm and classical

t-norm, respectively.

Conclusion 4.3 Balanced t-norm vanishes on the

squares [−1,0] × [0,1] and [0, 1] × [−1, 0].

Example 4.1 Let us consider the strong t-norm gen-

erated by the additive generator f(x) = (1−x)/x and

the strong t-conorm generated by the additive gener-

ator f(x) = x/(1 − |x|), c.f. (Klement et al., 2000;

Schweizer and Sklar, 1983). The formula p(x, y) =

−1

( f(x) + f(y)) deﬁnes the respective strong trian-

gular norms. The extension of this t-norm to balanced

Figure 4: Balanced t-conorm and balanced t-norm.

t-norm comes from the monotonicity and symmetry

axioms directly. Alternatively, the additive generator

f(x) = (1− x)/x of this classical t-norm could be ex-

tended to the interval [−1, 1] with the formula f(x) =

(1 − |x|)/x. Of course, this function is undeﬁned in

the point 0. The formula p(x,y) = f

−1

( f(x) + f(y))

deﬁnes the balanced t-norm for both arguments being

nonnegative or nonpositive.

The balanced counterpart of the strong t-conorm

generated by the additive generator f(x) = x/(1 −

|x|) is determined in the squares [0,1] × [0, 1] and

[−1,0] × [−1, 0]. The values in remaining parts of

the domain are unconstrained besides that they must

satisfy axioms of the deﬁnition. In this case we can

extend the additive generator to the whole interval

[−1,1] assuming that in points −1 and 1 it gets the

values −∞ and ∞, respectively. The balanced t-

conorm could be deﬁned by the formula S(x,y) =

−1

( f(x)+ f(y)) in its whole domain [−1,1]×[−1,1]

except the points (−1,1) and (1,−1), where this bal-

anced t-conorm is undeﬁned, c.f. (Homenda, 2003;

Klement et al., 2000; Schweizer and Sklar, 1983) for

details. Contour graphs of these two balanced norms

are presented in Figure 4.

5 BALANCED FUZZY SETS IN

DECISION MAKING

Let us consider simple decision making process in

real economical environment, i.e. with uncertain

premises. Assume that in the ﬁrst set of six premises

ﬁve have the numerical value 0.6 and the last one has

the value 0.4. In the second set of six premises the

one has numerical value 0.6 and ﬁve other have nu-

merical values 0.4. Classical fuzzy connectives em-

ployed as aggregators of premises do not distinguish

between these two sets. Max and min operators pro-

duce the same values for both sets: 0.6 and 0.4, re-

spectively. Employing the strong t-conorm based on

the additive operator f(x) = x/(1− x) we get the val-

ues 0.89 and 0.83 for both sets, respectively. In the

case of dual t-norm we get the respective values equal

to 0.17 and 0.11. The linear mapping f (x) = 2x − 1

to the interval [−1,1] gives the transformed values of

premises equal to 0.2 and −0.2 instead of 0.6 and

0.4. Classical triangular norms produce the following

the respective values: 0.78, 0.66 and −0.66, −0.78.

Therefore, besides small quantitative differences be-

tween aggregated numerical results no qualitative in-

dication is given with regard to the decision. Employ-

ing balanced modelling based on the additive opera-

tor f (x) = x/(1−|x|) balanced t-conorm produces the

values 0.50 and −0.50 for both sets of premises, re-

spectively. Dual balanced t-norm produces the values

0.06 and −0.06, respectively. In the case of balanced

modelling clear indication is given with regard to the

decision.

6 CONCLUSIONS

The balanced extension of fuzzy sets discussed in

this paper is a contribution to the discussion on sub-

jects of negative information and symmetry of nega-

tive/positive types of information. These aspects of

information processing, though controversial in clas-

sical and traditional ﬁelds of information processing,

become useful and necessary in some important areas

of research and practice, as indicated in Section 3 and

have been studied in number of papers.

Negative and positive types information play im-

portant role in information aggregation. Multicriteria

decision making process could be seen as a kind of in-

formation aggregation leading to a synthetical result

applicable in unique choice between given options.

The synthesis must consider pros and contras a deci-

sion, must consider positive and negative premisses of

the decision. The concept of balanced fuzzy sets deals

with positiveness and negativeness assuming symme-

try of both types of information.

In (Homenda and Pedrycz, 2005) the concept of

negativeness and symmetry was applied in construc-

tion of the balanced computing unit, a variation of

fuzzy neuron. The concept of balanced computing

unit involves a generalization of balanced t-norms, so

called t-norms in weak form. The balanced comput-

ing unit based on weak form of fuzzy connectives may

exemplify decision making process with positive and

negative premises.

REFERENCES

Atanassov, K. T. (1986). Intuitionistic fuzzy sets. Fuzzy

Sets and Systems, 20:87–96.

Buchanan, B. and Shortliffe, E. (1984). Ruled Based Ex-

pert Systems, The MYCIN Experiment of the Stanford

Heuristic Programming Project. Addison-Wesley,

Reading, MA.

Calvo T., e. a. (2001). The functional equations of frank

and alsina for uninorms and nullnorms. Fuzzy Sets

and Systems, 120:15–24.

Detyniecki, M. (2000). Mathematical Aggregation Oper-

ators and their Application to Video Querying. PhD

thesis, l’Universite Paris VI.

Detyniecki, M. and Bouchon-Meunier, B. (2000a). Aggre-

gating truth and falsity values. In Proc. of the Int.

Conf. on Information Fusion - FUSION’2000, Paris,

France, July 2000, pages 18–24.

Detyniecki, M. and Bouchon-Meunier, B. (2000b). Build-

ing an aggregation operator with a balance. In Proc.

of the Int. Conf. on Information Processing and Man-

agement of Uncertainty in Knowledge-Based Systems,

Madrid, Spain, July 2000, pages 686–692.

Dubois, D. and Prade, H. (1983). Twofold fuzzy sets:

an approach to the representation of sets with fuzzy

boundaries based on possibility and necessity mea-

sures. Journal of Fuzzy Mathematics, 3(4):53–76.

Gau, W. L. and Buehrer, D. J. (1993). Vague sets.

IEEE Transactions on Systems, Man, and Cybernet-

ics, 23:610–614.

Grabisch M., e. a. (2002). On symmetric pseudo-additions

and pseudo-multiplications: Is it possible to built

rings on [-1,+1]? In The 9th Int. Conf. on Infor-

mation Processing and Management of Uncertainty

in Knowledge-Based Systems, IPMU 2002, 1-5 July,

France.

Homenda, W. (2001). Balanced fuzzy sets. Preprint, Fac-

ulty of Mathematics and Information Science, Warsaw

University of Technology.

Homenda, W. (2003). Triangular norms, uni- and null-

norms, balanced norms: the cases of the hierarchy of

iterative operators. In Proc. of the 24th Linz Seminar

on Fuzzy Set Theory, Linz, Feb. 4-8, pages 27–35.

Homenda, W. (2004). Balanced norms: from triangular

norms towards iterative operators, pages 251–262. in:

Soft Computing, Foundations and theoretical aspects.

Academic Publishing House EXIT, Warsaw.

Homenda, W. and Pedrycz, W. (1991). Processing of uncer-

tain information in linear space of fuzzy sets. Fuzzy

Sets and Systems, 44:187–198.

Homenda, W. and Pedrycz, W. (2002). Symmetrization of

fuzzy operators: notes on data aggregation. In Proc. of

the Int. Conf. on Fuzzy Systems and Knowledge Dis-

covery, Singapore, Nov. 18-22.

Homenda, W. and Pedrycz, W. (2005). Balanced fuzzy

computing unit. Int. Journal of Uncertainty, Fuzziness

and Knowledge-Based Systems, 13(2):117–138.

Kahneman, D. and Tversky, A. (2004). Prospect Theory:

An Analysis of Decision under Risk, volume XVLII

of in: Soft Computing, Foundations and theoretical

aspects, pages 263–291. Econometrica.

Klement, E. P., Mesiar, R., and Pap, E. (2000). Triangular

norms. Kluwer Academic Pub., Dordrecht.

Ovchinnikov, S. (1998). On Robust Aggregation Proce-

dures, pages 3–10. Econometrica.

Schweizer, B. and Sklar, A. (1983). Probabilistic Metric

Spaces. North Holland, New York.

Silvert, W. (1979). Symmetric summation: A class of op-

erations on fuzzy sets. IEEE Trans. System, Man, Cy-

bernetics, 9:659–667.

Yager, R. R. (1988). On ordered weighted averaging aggre-

gation operators. IEEE Trans. System, Man, Cyber-

netics, 18:183–190.

Yager, R. R. (1993). Families of owa operators. Fuzzy Sets

and Systems, 59:125–148.

Yager, R. R. and Rybalov, A. (1996). Uninorm aggregation

operators. Fuzzy Sets and Systems, 80:111–120.

Yager, R. R. and Rybalov, A. (1998). Full reinforcement op-

erators in aggregation techniques. IEEE Transactions

on Systems, Man and Cybernetics, 28:757–769.

Zadeh, L. A. (1965). Fuzzy sets. Inform. And Control,

8:338–353.

Zhang W. R., e. a. (1989). Pool2, a generic system for cog-

nitive map development and decision analysis. IEEE

Tran. on Systems, Man and Cybernetics, 19:31–39.