VCODEX: A DATA COMPRESSION PLATFORM

Kiem-Phong Vo

AT&T Labs, Shannon Laboratory, 180 Park Avenue, Florham Park, NJ 07932, USA

Keywords:

Data compression, transformation.

Abstract:

Vcodex is a platform to compress and transform data. A standard interface, data transform, is deﬁned to rep-

resent any algorithm or technique to encode data. Although primarily geared toward data compression, a data

transform can perform any type of processing including encryption, portability encoding and others. Vcodex

provides a core set of data transforms implementing a wide variety of compression algorithms ranging from

general purpose ones such as Huffman or Lempel-Ziv to structure-driven ones such as reordering ﬁelds and

columns in relational data tables. Such transforms can be reused and composed together to build more com-

plex compressors. An overview of the software and data architecture of Vcodex will be presented. Examples

and experimental results show how compression performance beyond traditional approaches can be achieved

by customizing transform compositions based on data semantics.

1 INTRODUCTION

Modern business systems routinely manage huge

amounts of data. For example, the daily volumes of

billing and network management data generated by an

international communication company involve tens to

hundreds of gigabytes (Fowler et al., 2004). Further,

certain of such data is required by laws to be kept on-

line for several years. Thus, data compression is a

critical component in these systems.

Much of compression research has traditionally

been focused on developing general purpose tech-

niques which treat data as unstructured streams of

bytes. Algorithms based primarily on either pattern

matching, statistical analysis or some combination

thereof (Huffman, 1952; Jones, 1991; Witten, 1987;

Ziv and Lempel, 1977; Ziv and Lempel, 1978) de-

tect and remove different forms of information re-

dundancy in data. Well-known compression tools

such as the ubiquitous Unix Gzip or Windows Winzip

are based on such general purpose techniques, for

example, the Lempel-Ziv compression method (Ziv

and Lempel, 1977) and Huffman coding (Huffman,

1952). A recently popular compressor, Bzip2 (Se-

ward, 1994), ﬁrst reorders data by the famous BWT or

Burrows-Wheeler Transform (Burrows and Wheeler,

1994) to induce better compressibility before passing

it to other compressors.

Structures in data often provide a good source

of information redundancy that can be exploited to

improve compression performance. For example,

columns or ﬁelds in relational data tend to be sparse

and may share non-trivial relationships. Buchsbaum

et al (Buchsbaum et al., 2003) developed the Pzip

technique that assumes some conventional compres-

sor such as Gzip and groups table columns to improve

their compressibility by such a compressor. Vo and

Vo (Vo and Vo, 2004; Vo and Vo, 2006) took a dif-

ferent approach to the same problem and showed how

to use dependency relations among table columns to

rearrange data for better compressibility. For a dif-

ferent class of data, namely XML, the Xmill com-

pressor (Liefke and Suciu, 2000) works in a similar

spirit to Pzip by grouping parts of a document with

the same tags to be compressed by some conventional

compressor.

In practice, data often consist of ad-hoc mix-

tures of structures beyond just simple tables or sin-

gle XML documents. For example, a log ﬁle gen-

erated by some network management system might

contain many records pertaining to different network

events. Due to their common formats, the records

belonging to a particular event might form a table.

As such, the compressibility of such a log ﬁle could

be enhanced by grouping records by event types ﬁrst

before compressing each group by one of the above

Vo K. (2007).

VCODEX: A DATA COMPRESSION PLATFORM.

In Proceedings of the Second International Conference on Software and Data Technologies - SE, pages 81-89

DOI: 10.5220/0001344600810089

 SciTePress

table compressors. Unfortunately, from the point of

view of building compression tools, it is hard, if not

impossible, to automatically detect and take advan-

tage of such ad hoc structures in data. Nonethe-

less, this points out that, in each particular circum-

stance, optimum compression performance may re-

quire the ability to form arbitrary compositions of

diverse data transformations, both generic and data-

speciﬁc. Indeed, this ability is implicitly needed even

in implementing general purpose compressors such as

Gzip and Bzip2 that combine distinct techniques deal-

ing with different aspects of information redundancy.

Thus, a major challenge to compression research as

well as to practical use of compression on large scale

data is to provide a way to construct, reuse and in-

tegrate different data transformation and compression

techniques to suit particular data semantics. This is

the problem that the Vcodex platform addresses.

Central to Vcodex is the notion of data transforms

or software components to alter data in some invert-

ible ways. As it is beyond the scope of this paper,

we only mention that by taking this general approach

to data transformation Vcodex can also accommodate

techniques beyond compression such as encryption,

translation between character sets or just simple cod-

ing of binary data for portability. For maximum us-

ability, two main issues must be addressed:

• Deﬁning a standard software interface for data

transforms: A standardized software interface

helps transform users as it eases implementation

of applications and ensures that application code

remains stable when algorithms change. Trans-

form developers also beneﬁt as a standard inter-

face simpliﬁes and encourages reuse of existing

techniques in implementing new ones.

• Deﬁning a self-describing and portable standard

data format: As new data transforms may be

continually developed by independent parties, it

is important to have a common data format that

can accommodate arbitrary composition of trans-

forms. Such a format should allow receivers of

data to decode them without having to know how

they were encoded. In addition, encoded data

should be independent of OS and hardware plat-

forms so that they can be easily transported and

shared.

The rest of the paper gives an overview of the

Vcodex platform and how it addresses the above

software and data issues. Experiments based on

the well-known Canterbury Corpus (Bell and Powell,

2001) for testing data compressors shows that Vcodex

could far outperform conventional compressors such

as Gzip or Bzip2.

2 SOFTWARE ARCHITECTURE

Vcodex is written in the C language in a style com-

patible with C++. The platform is divided into two

main layers. The base layer is a software library

deﬁning and providing a standard software interface

for data transforms. This layer assumes that data are

processed in segments small enough to ﬁt entirely in

memory. The library can be used directly by applica-

tions written in C or C++ in the same way that other C

and C++ libraries are used. A command tool Vczip is

written on top of the library layer to enable ﬁle com-

pression without low-level programming. Large ﬁles

are handled by being broken into chunks with suitable

sizes for in-memory processing.

2.1 Library Design

Transformation handle and operations

Vcodex t – maintaining contexts and states

vcopen(), vcclose(), vcapply(), ...

Discipline structure Data transforms

Vcdisc t Vcmethod t

Parameters for data processing, Burrows-Wheeler, Huffman,

Event handler Delta compression, Table transform, etc.

Figure 1: A discipline and method library architecture for

Vcodex.

Figure 1 summarizes the design of the base

Vcodex library which was built in the style of the Dis-

cipline and Method library architecture (Vo, 2000).

The top part shows that a transformation handle of

type Vcodex t provides a holding place for contexts

used in transforming different data types as well as

states retained between data transformation calls. A

variety of functions can be performed on such han-

dles. The major ones are vcopen() and vcclose()

for handle opening and closing and vcapply() for

data encoding or decoding. A transformation han-

dle is parameterized by an optional discipline struc-

ture of type Vcdisc t and a required data transform

of type Vcmethod t. Each discipline structure is sup-

plied by the application and provides additional infor-

mation about the data to be processed. On the other

hand, a data transform is selected from a predeﬁned

set and speciﬁes the transformation technique. Sec-

tion 2.2 describes a few common data transforms such

as Burrows-Wheeler, Huffman, etc. Complex data

transformations can be composed from simpler ones

by passing existing handles into newly opened han-

dles for additional processing.

Figure 2 shows an example to construct and use a

transformation handle for delta compression by com-

posing two data transforms: Vcdelta and Vchuffman

(Section 2.2). Here, delta compression (Hunt et al.,

1998) is a general technique to compress a target

ICSOFT 2007 - International Conference on Software and Data Technologies

1. typedef struct _vcdisc_s

2. { void* data;

3. ssize_t size;

4. Vcevent_f eventf;

5. } Vcdisc_t;

6. Vcdisc_t disc = { "Source data to compare against", 30, 0 };

7. Vcodex_t* huff = vcopen(0, Vchuffman, 0, 0, VC_ENCODE);

8. Vcodex_t* diff = vcopen(&disc, Vcdelta, 0, huff, VC_ENCODE);

9. ssize_t cmpsz = vcapply(diff, "Target data to compress", 23, &cmpdt);

Figure 2: An example of delta compression.

data given a related source data. It is often used to

construct software patches or to optimize storage in

revision control systems (Tichy, 1985). The trans-

form Vcdelta implements a generalized Lempel-Ziv

parsing technique for both delta and normal compres-

sion whose data format was the subject of the IETF

(Internet Engineering Task Force) VCDIFF Proposed

Standard RFC3284 (Korn et al., 2002; Korn and Vo,

2002).

• Lines 1–6 show the type of a discipline structure

and disc, an instance of it. The ﬁelds data and

size of disc provide any source data available to

compare against in delta compression. Even if no

source data is given, the target data would still

be compressed in the usual Lempel-Ziv fashion,

i.e., by factoring out repeating patterns. The ﬁeld

eventf of disc is optional and, if used, speciﬁes a

function to process events such as handle opening

and closing.

• Lines 7 and 8 show handle creation and composi-

tion. The Huffman coding handle huff is created

ﬁrst. The ﬁrst and second arguments to vcopen()

specify the optional discipline structure, e.g., disc

on line 8, and the selected data transform, e.g.,

Vchuffman on line 7. Variants or modes of a trans-

form can be given in the third argument (see the

examples in Figure 5). The fourth argument is

used to compose a transform with another one.

For example, on line 8, the handle huff is used

to further compress the output of diff. The last

argument of vcopen() must be one of VC ENCODE

or VC DECODE to tell if the handle is opened for en-

coding or decoding.

• Line 9 gives an example of calling vcapply() to

compress some given data. The compressed result

is returned in cmpdt while its size is returned by

the call. A transform such as Vcdelta creates mul-

tiple output data segments coding different types

of data (Section 3). Each such segment would

be separately passed to the follow-on transforma-

tion handle, in this case, huff. As such, huff can

generate the appropriate Huffman codes to match

with each segment and improve compression per-

formance. Note also that the source data in the

discipline structure disc could be changed before

each vcapply() call to match with the data to be

compressed.

The above example shows the encoding side.

The decoding side is exactly the same except that

VC DECODE replaces VC ENCODE and the data passed

to vcapply() would be some previously compressed

data. An advantage in being able to write applica-

tion code based on a standard interface as provided is

that algorithmic enhancement of the data transform in

use does not require changes at the application level.

In addition, experimentation with different data trans-

forms only need minimal code editing.

2.2 Data Transforms

1. typedef struct _vcmethod_s

2. { ssize_t (*encodef)(Vcodex_t*, void*, ssize_t, void**);

3. ssize_t (*decodef)(Vcodex_t*, void*, ssize_t, void**);

4. int (*eventf)(Vcodex_t*, int, void*);

5. char* name;

6. ...

7. } Vcmethod_t;

Figure 3: The type of a data transform.

Figure 3 shows Vcmethod t, the type of a data

transform. Lines 2 and 3 show that each transform

provides two functions for encoding and decoding.

An optional event handling function eventf, if pro-

vided, is used to process certain events. For example,

some transforms maintain states throughout the life-

time of a handle. The structures to keep such states

would be created or deleted at handle opening and

closing via such event handling functions. Each trans-

form also has a name that uniquely identiﬁes it among

the set of all available transforms. This name is en-

coded in the output data (Section 3) to make the en-

coded data self-describing.

Vcodex provides a large collection of trans-

forms for building efﬁcient compressors of general

and structured data including a number that are

application-speciﬁc. Below are brief overviews of a

few important data transforms:

• Vcdelta: This implements a delta compres-

sor based on a generalized Lempel-Ziv parsing

method. It outputs data in the Vcdiff encoding

format as described in the IETF Proposed Stan-

dard RFC3284 (Korn et al., 2002).

• Vcsieve: This transform used approximate

matching to perform delta compression as well

as compression of genetic sequences, a class of

data notoriously difﬁcult to compress (Manzini

and Rastero, 2004).

• Vcbwt: This implements the Burrows-Wheeler

transform.

VCODEX: A DATA COMPRESSION PLATFORM

• Vctranspose: This treats a dataset as a table, i.e.,

a two-dimension array of bytes, and transposes it.

• Vctable: This uses column dependency (Vo and

Vo, 2006) to transform table data and enhance

their compressibility.

• Vcmtf: This provides the move-to-front data trans-

form (Bentley et al., 1986) and a predictive vari-

ant of it. The predictive variant uses a heuristic

algorithm that keeps track of how often a charac-

ter follows another and, when favorable, moves it

to the front as soon as its predecessor is encoded.

• Vcrle: This provides the run-length encoder and

a variant that only encodes runs of zeros using a

special binary coding method (Deorowicz, 2000).

• Vchuffman: This implements static Huffman cod-

ing.

• Vchuffgroup: This is implemented on top of

Vchuffman. It divides data into short segments of

equal length and groups segments compress well

together with a single Huffman code table.

• Vcama: This collects records with the same length

together to form tables that could then be com-

pressed via Vctable. It was originally written to

deal with an arcane data format speciﬁc to tele-

phone data called AMA, hence the name. But it

can also handle other general record types.

• Vcmap: This provides a collection of methods to

map data from one character set to another. For

example, different variants translate data between

ASCII and various versions of EBCDIC.

2.3 The Vczip Command

The Vczip command enables usage of the available

data transforms without low level programming. It

provides a syntax to compose different transforms to-

gether to process a data ﬁle. In this way, end users can

experiment with different combinations of transforms

on their data to optimize compressibility.

Figure 4 shows the transform composition syntax.

Lines 1 and 2 show that each transform is speciﬁed by

a name, e.g., delta or table, followed by an optional

sequence of arguments depending on the particular

transform. Lines 3 and 4 show that such arguments

are separated by periods. Lines 5 and 6 show that the

list of transforms can be empty to signify usage of a

default compression method deﬁned by Vczip. But

if not, it must start with -m and follow by a comma-

separated sequence of transforms.

Figure 5 shows a snapshot of an experiment to

explore different ways to compress data using Gzip,

Bzip2 and various compositions of Vcodex data trans-

forms. The ﬁle kennedy.xls was an Excel spreadsheet

taken from the Canterbury Corpus (Bell and Powell,

2001).

• Lines 1–6 show the raw size of kennedy.xls and

compression results by Gzip and Bzip2. Gzip

compressed the data by roughly a factor of 5 while

Bzip2 achieved a factor of 8 to 1.

• Lines 7–10 show Vczip instantiated as different

variations of a BWT compressor. The 0 argument

to the run length encoding transform rle meant

that only runs of 0’s were coded. The same argu-

ment to the move-to-front transform mtf restricted

it to moving a data byte only after access. As that

was analogous to Bzip2, about the same perfor-

mance resulted. On the other hand, line 9 used

a variant that aggressively predicted and moved

data (Section 2.2) resulting in a 12 to 1 compres-

sion factor.

• Lines 11-14 show the use of the table transform

Vctable (Vo and Vo, 2006) to treat the data as a

2-dimensional array of bytes and reorder data by

column dependency before running same back-

end data transforms as earlier. The compression

factor improved to about 19 to 1 with that. Insert-

ing the Burrows-Wheeler transform after the table

transform further improved the compression fac-

tor to nearly 30 to 1.

• Line 15 shows that the compressed data was de-

coded into a ﬁle x and compared against the orig-

inal data to test correctness. As shown, decom-

pression would always be done with the option -u,

i.e., no knowledge of transforms used on encoding

required.

Figure 6 shows another experiment to compress

a large ﬁle of telephone data in a proprietary format

called AMA. This type of data consists of records in

which the ﬁrst 4 bytes of a record tell the length of

the record. The Vcama transform collected records of

the same length together before passing them to the

column dependency table transform Vctable. Again,

this ability to exploit structures in data resulted in the

best compression performance.

3 DATA ARCHITECTURE

The output of a transformation is data to store or trans-

port. For maximal usability, the main issues to be ad-

dressed are: portability and self-description. Porta-

bility means that primitive types such as bits, integers

and strings should be standardly encoded so that data

ICSOFT 2007 - International Conference on Software and Data Technologies

1. Transform -> {delta, table, bwt, huffman, ama, ...}

2. Transform -> {delta, table, bwt, huffman, ama, ...} . Arglist(Transform)

3. Arglist(Transform) -> Nil

4. Arglist(Transform) -> Arg(Transform) . Arglist(Transform)

5. TransformList -> Nil

6. TransformList -> "-m" TransformList , Transform

Figure 4: Language syntax to compose transforms.

1. ls -l kennedy.xls

2. -rw------- 4 kpv 1029744 Nov 11 1996 kennedy.xls

3. gzip < kennedy.xls > out; ls -l out

4. -rw-r--r-- 1 kpv 206767 Apr 11 12:30 out

5. bzip2 < kennedy.xls > out; ls -l out

6. -rw-r--r-- 1 kpv 130280 Apr 11 12:30 out

7. vczip -mbwt,mtf.0,rle.0,huffgroup < kennedy.xls > out; ls -l out

8. -rw-r--r-- 1 kpv 129946 Apr 11 12:31 out

9. vczip -mbwt,mtf,rle.0,huffgroup < kennedy.xls > out; ls -l out

10. -rw-r--r-- 1 kpv 84281 Apr 11 12:31 out

11. vczip -mtable,mtf,rle.0,huffgroup < kennedy.xls > out; ls -l out

12. -rw-r--r-- 1 kpv 53918 Apr 11 12:31 out

13. vczip -mtable,bwt,mtf,rle.0,huffgroup < kennedy.xls > out; ls -l out

14. -rw-r--r-- 1 kpv 35130 Apr 11 12:31 out

15. vczip -u < out >x; cmp x kennedy.xls

Figure 5: Experimenting with different combinations of data transforms.

can be produced on one OS/hardware platform and

transparently decoded on another. Self-description

means that data can be decoded without knowledge

of how they were encoded.

3.1 Portable Data Encoding

Transform writers must take care to ensure portability

of output data. Vcodex provides a variety of func-

tions to encode strings, bits, and integers in portable

forms. String data are assumed to be in the ASCII

character set. When running programs on a platform

not based on ASCII, for example, IBM mainframes

with EBCDIC, a function vcstrcode() can be used

to transcribe string data from the native character set

into ASCII for storage. For example, the identiﬁca-

tion string of a data transform is often constructed

from its name (Section 2.2). As the name is in the

native character set, it would need to be translated to

ASCII for portability.

For bit encoding, it is assumed that the fundamen-

tal unit of storage is an 8-bit byte. The bits in a byte

are position from left to right, i.e., the highest bit is at

position 0, the second highest bit at position 1, and so

on. Then a sequence of bits would be simply imposed

onto a sequence of bytes in that order. For example,

the 12-bit sequence 101010101111 would be coded in

the 2-byte sequence 170 240. That is, the ﬁrst eight

bits, 10101010, are stored in a byte so that byte would

have value 170. The last four bits, 1111, are padded

with 0’s before storage so the representing byte would

have value 240.

Integers are unsigned and encoded in a variable-

sized format originally introduced in the Sﬁo li-

brary (Korn and Vo, 1991). Each integer is treated as

a number in base 128 so that each digit can be stored

in a single byte. Except for the least signiﬁcant one,

each byte would turn on its most signiﬁcant bit, MSB,

to indicate that the next byte is a part of the encoding.

For example, consider the integer 123456789 which

is represented by four digits 58, 111, 26, 21 in base

128. Below are the coding of these digits shown in

bits for clarity.

VCODEX: A DATA COMPRESSION PLATFORM

1. ls -l ningaui.ama

2. -rw-r--r-- 1 kpv kpv 73452794 Sep 12 2005 ningaui.ama

3. gzip < ningaui.ama >out; lsl out

4. -rw-r--r-- 1 kpv kpv 30207067 Apr 11 12:55 out

5. bzip2 < ningaui.ama >out; lsl out

6. -rw-r--r-- 1 kpv kpv 22154475 Apr 11 12:57 out

7. vczip -mama,table,mtf,rle.0,huffgroup < ningaui.ama >out; lsl out

8. -rw-r--r-- 1 kpv kpv 20058182 Apr 11 13:00 out

Figure 6: Compression based on data-speciﬁc structures.

10111010 11101111 10011010 00010101

MSB+58 MSB+111 MSB+26 0+21

3.2 Self-describing Data

A large ﬁle might need to be divided into segments

small enough to process in memory. Each such seg-

ment is called a window. The internal representation

of a transformed window would depend on what data

transforms were used. But at the ﬁle level, that can be

treated simply as a sequence of bytes.

1. [ID_file:] 0xd6 0xc3 0xc4 0xd8

2. [Reserved:] Size Data

3. [Transforms:] Size

4. [Transform1:] ID_transform

5. [Argument:] Size Data

6. [Transform2:] ID_transform

7. [Argument:] Size Data

8. ...

9. [Window1:] Indicator

10 [Transformed data]: Size Data

11. [Window2:] Indicator

12 [Transformed data]: Size Data

13. ...

Figure 7: The self-describing format of transformed data.

Figure 7 shows the structure of encoded data in

which each ﬁle consists of a set of header data fol-

lowed by one or more Window sections and gives an

example of header data.

• Line 1 shows that each ﬁle is identiﬁed by four

starting bytes which are the ASCII letters V, C, D

and X with their high bits on.

• Line 2 shows a Reserved section usable by an ap-

plication to store additional data. As shown here

and later, each data element is represented by a

Size and Data pair that tells number of data bytes

followed by the data itself.

• Lines 3–8 show the Transforms section which

encodes the original composition of transforms.

This starts with Size, the length in bytes of the

rest of the section. Each transform consists of an

identiﬁcation string which, by convention, must

be in ASCII followed by any additional data.

• Lines 9–13 show the list of Window sections.

Each window section starts with an Indicator

byte which can be one of the values VC RAW,

VC SOURCEFILE and VC TARGETFILE. VC RAW means

that the encoded data were not transformed. The

latter two values are as deﬁned in the Vcdiff Pro-

posed Standard RFC3284 (Korn et al., 2002) to

indicate that the data was delta compressed (Hunt

et al., 1998) against data from either the source or

target ﬁle respectively. Following the Indicator

byte is the transformed data.

0xd6 0xc3 0xc4 0xd8 [ID_file]

0 [Reserved size]

16 [Transforms size]

delta\0 [ID_transform]

0 [Argument size]

huffman\0 [ID_transform]

0 [Argument size]

Figure 8: Header data and data schema of a delta compres-

sor.

Figure 8 gives an example based on a delta

compressor resulted from composing the transforms

Vcdelta and Vchuffman. The top part shows ﬁrst the

literal bytes deﬁning the header data which essen-

ICSOFT 2007 - International Conference on Software and Data Technologies

tially only coded the names of the transforms. The

bottom part shows pictorially the various components

of a compressed ﬁle. Each ﬁle starts with the header

data which tells the ﬁle type via the four magic bytes

VCDX and the transform composition sequence. The

compressed data are divided into a sequence of win-

dows. The raw data in each window is processed

ﬁrst by Vcdelta to generate the so-called delta in-

structions deﬁned in the IETF RFC3284 (Korn et al.,

2002). In this method, three different sections of data

are generated, instructions, addresses of matches and

unmatched data. Each section would then be pro-

cessed separately by the following Huffman compres-

sor Vchuffman. Partitioning of data by types in this

way helps to improve compression as the different

sections often have distinct statistical properties.

4 PERFORMANCE

An experiment was done to test compression perfor-

mance by tailoring transform compositions to partic-

ular data. The small and large ﬁles from Canterbury

Corpus (Bell and Powell, 2001) were used to compare

Vczip, Gzip and Bzip2. Sizes were measured in bytes

and times in seconds. Timing results were obtained

on a Pentium 4, 2.8GHZ, with 1Gb RAM, running

Redhat Linux.

Figure 9 presents compression and timing data in

two tables. The top and bottom parts of each ta-

ble show results of the small and large ﬁles respec-

tively. The Algs entries show the algorithm composi-

tions used to compress the ﬁles. Below are the algo-

rithms:

• B: The Burrows-Wheeler transform Vcbwt.

• M: The move-to-front transform Vcmtf with predic-

tion.

• R: The run-length encoder Vcrle with coding only

runs of 0’s.

• h: The Huffman coder Vchuffman.

• H: The Huffman coder with grouping

Vchuffgroup.

• T: The table transform Vctable.

• S: The delta compressor Vcsieve using approxi-

mate matching.

• D: The transform Vcsieve with reverse matching

and mapping of the letter pairs A and T, G and C,

etc.

The Bits entries show the average number of bits

needed to encode a byte with each row’s overall win-

ner in bold. Vczip only lost slightly to Bzip2 on

cp.html and to Gzip on grammar.lsp. Its weighted

compression rates of 1.21 bits per byte for the small

ﬁles and 1.68 for the large ﬁles outdid the best re-

sults of 1.49 and 1.72 shown at the Corpus website.

The pure Huffman coder Vchuffman outperformed its

grouping counterpart Vchuffgroup on small ﬁles as

the cost of coding groups became too expensive in

such cases.

The best cases of Vczip typically ran somewhat

slower than Bzip2 and Gzip. Although some speed

loss was due to the general nature of transform com-

position, the major part was due to sophisticated al-

gorithms such as move-to-front with prediction. In

practice, applications often make engineering choices

between faster data transforms with worse compres-

sion vs. slower ones with better compression.

For any collection of transforms, the number of

algorithm combinations that make sense tend to be

small and dictated by the nature of the transforms.

For example, Huffman coding should never be used

before other transforms as it destroys any structure in

data. Thus, although not done here, it is possible to

ﬁnd an optimal composition sequence by trying all

candidate composition sequences on small data sam-

ples.

5 RELATED WORKS

Vcodex introduces the notion of data transforms as

standard software components to encapsulate com-

pression algorithms for reusability. A variety of

library packages such as zlib (Gailly and Adler,

2005) or bzlib (Seward, 1994) also aim at improving

reusability. However, except for their overall external

compression interface, the constituent algorithms in

these packages are buried in the implemented code.

For example, although Huffman coding is required

in both zlib and bzlib, different versions were hard-

coded with incompatible data formats. By contrast,

new Vcodex data transforms are often crafted from

existing ones via either composition or direct usage

in implementation. Application systems with propri-

etary data types may also develop special data trans-

forms for such types to enhance compressibility. In

this way, exotic compositions of compression algo-

rithms can be made to ﬁt any particular data semantics

and gain optimal compression performance.

A side of data compression often overlooked is the

design of the output data. If not carefully done, such

data may not be sharable across machines due to dif-

ferent architectures or may become stale and unusable

over time due to algorithm evolution. Unfortunately,

few compression tools have ever published their cod-

VCODEX: A DATA COMPRESSION PLATFORM

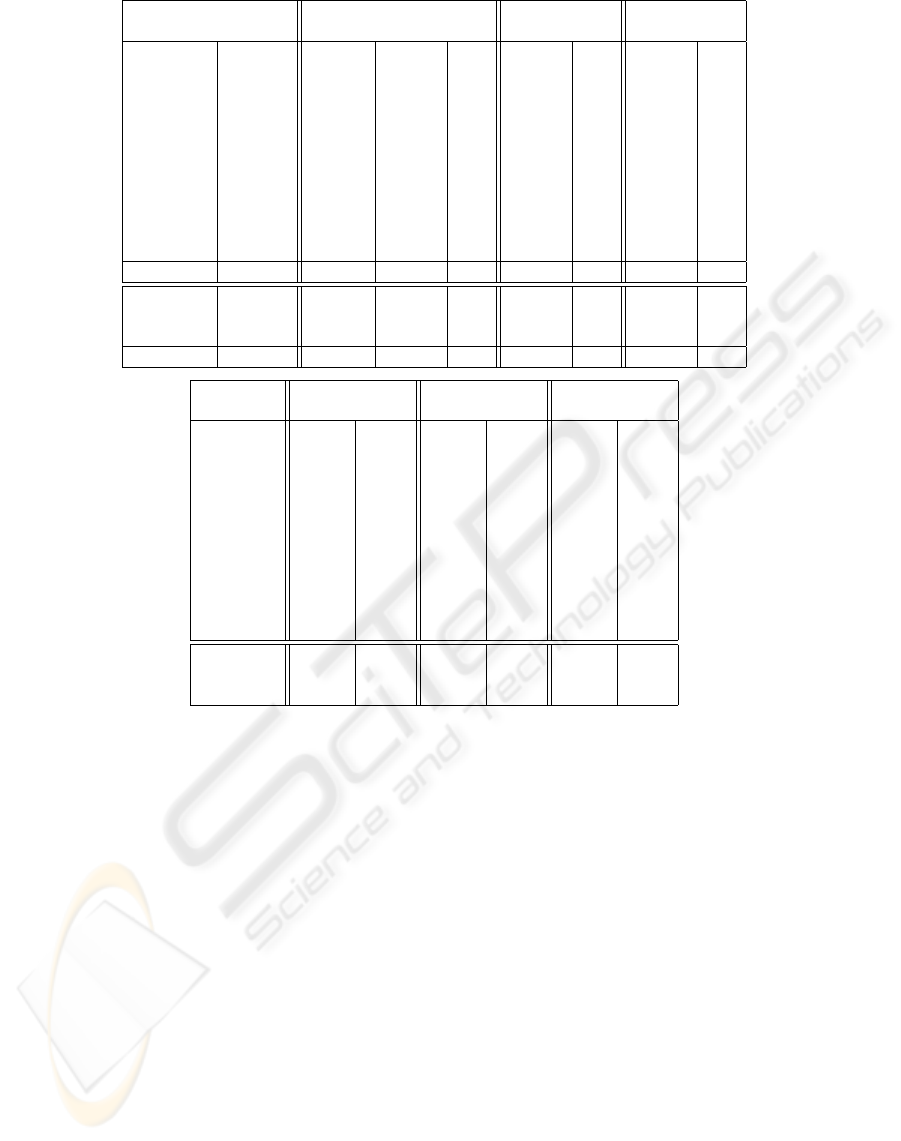
Vczip Bzip2 Gzip

File Size Algs Cmpsz Bits Cmpsz Bits Cmpsz Bits

alice29.txt 152089 BMRH 42654 2.24 43202 2.27 54423 2.86

ptt5 513216 TBMRH 33149 0.52 49759 0.78 56438 0.88

ﬁelds.c 11150 BMRh 3036 2.18 3039 2.18 3134 2.25

kennedy.xls 1029744 TBMRH 35130 0.27 130280 1.01 206767 1.61

sum 38240 SBMRH 12406 2.60 12909 2.70 12920 2.70

lcet10.txt 426754 BMRH 105778 1.98 107706 2.02 144874 2.72

plrabn12.txt 481861 BMRH 143817 2.39 145577 2.42 195195 3.24

cp.html 24603 BMRh 7703 2.50 7624 2.48 7991 2.60

grammar.lsp 3721 BMRh 1274 2.74 1283 2.76 1234 2.65

xargs.1 4227 BMRh 1728 3.27 1762 3.33 1748 3.31

asyoulik.txt 125179 BMRH 39508 2.52 39569 2.53 48938 3.13

Total 2810784 426183 1.21 542710 1.54 733662 2.09

E.coli 4638690 DH 1137801 1.96 1251004 2.16 1341243 2.31

bible.txt 4047392 BMRH 786709 1.55 845623 1.67 1191061 2.35

world192.txt 2473400 BMRH 425077 1.37 489583 1.58 724593 2.34

Total 11159482 2349587 1.68 2586210 1.85 3256897 2.33

Vczip Bzip2 Gzip

File Cmptm Dectm Cmptm Dectm Cmptm Dectm

alice29.txt 0.05 0.01 0.03 0.01 0.01 0.01

ptt5 0.27 0.08 0.03 0.01 0.02 0.01

ﬁelds.c 0.01 0.01 0.01 0.01 0.01 0.01

kennedy.xls 0.27 0.18 0.23 0.07 0.11 0.01

sum 0.03 0.01 0.01 0.01 0.01 0.01

lcet10.txt 0.17 0.08 0.12 0.06 0.05 0.01

plrabn12.txt 0.21 0.11 0.15 0.09 0.08 0.01

cp.html 0.01 0.01 0.01 0.01 0.01 0.01

grammar.lsp 0.01 0.01 0.01 0.01 0.01 0.01

xargs.1 0.01 0.01 0.01 0.01 0.01 0.01

asyoulik.txt 0.04 0.01 0.02 0.01 0.01 0.01

E.coli 7.85 0.10 1.92 1.03 1.93 0.08

bible.txt 2.47 1.04 1.64 0.72 0.55 0.06

world192.txt 1.31 0.62 1.04 0.42 0.23 0.03

Figure 9: Compression size (bytes), rate (bits/byte) and time (seconds) for the Canterbury Corpus.

ing formats. Two rare exceptions are the Deﬂate For-

mat (Deutsch, 1996) used in Gzip and the Vcdiff For-

mat (Korn et al., 2002) for delta encoding which have

been standardized and sanctioned by the Internet En-

gineering Task Force to facilitate transporting of com-

pressed data over the Internet. An appealing feature

of the Vcodex self-describing data architecture is that

the data format of each transform can be kept in-

dependent from others that may be composed with

it in applications. This allows any speciﬁcation and

standardization effort to focus on the format of each

transform independently from others. This should be

contrasted, for example, with Deﬂate which must de-

ﬁne in details both the output of its main Lempel-Ziv

coder and also that of the low level Huffman coder

used to clean up any remaining statistical redundancy

in the Lempel-Ziv output.

6 CONCLUSION

Advances in compression are continually pulled by

two opposing forces: generalization to devise tech-

niques applicable to all data types and specialization

to devise techniques exploiting speciﬁc structures in

certain classes of data. General techniques such as

Lempel-Ziv or Burrows-Wheeler Transform are easy

to use and do perform well with most data. How-

ever, as seen in our experiments earlier, such tech-

niques could seldom match the performance of algo-

rithms speciﬁcally designed for classes of data such

as tables, DNA sequences, etc. Unfortunately, the

cost to develop data-speciﬁc compression tools can

quickly become prohibitive considering the plethora

of arcane data types used in large application systems.

Vcodex provides a unique solution to this problem by

applying a software and data engineering approach to

compression. Its data transform interface frees algo-

rithm designers to focus only on the data transfor-

ICSOFT 2007 - International Conference on Software and Data Technologies

mation task at hand without having to be concerned

with other transforms that they may require. Further,

users of compression also have the opportunity to mix

and match data transforms to optimize the compress-

ibility of their data without being locked into some

compositional sequences picked by the tool design-

ers. The best indication of success for Vcodex is that

the platform has been in use for a few years in a num-

ber of large data warehouse applications handling ter-

abytes of data daily. Tranform compositions properly

tailored to data types help achieving compression ra-

tios up to hundreds to one, resulting in signiﬁcant cost

savings. A variety of data transforms have been con-

tinually developed along with new data types without

disrupting ongoing usage. Further, as the number of

data types is limited per application system, simple

learning algorithms based on training with small sam-

ples of data could often be developed to automatically

ﬁnd optimal combinations of transforms for effective

compression. In this way, the platform has proven to

be an effective tool to help advancing compression not

just in specialization but also in generalization.

REFERENCES

T. Bell and M. Powell. The Canterbury Corpus,

http://corpus.canterbury.ac.nz. Technical Report,

2001.

J. Bentley, D. Sleator, R. Tarjan, and V. Wei. A Locally

Adapative Data Compression Scheme. Comm. of the

ACM, 29:320–330, 1986.

A. Buchsbaum, G.S. Fowler, and R. Giancarlo. Improving

Table Compression with Combinatorial Optimization.

J. of the ACM, 50(6):825–51, 2003.

M. Burrows and D.J. Wheeler. A Block-Sorting Lossless

Data Compression Algorithm. Report 124, Digital

Systems Research Center, 1994.

S. Deorowicz. Improvements to Burrows-Wheeler Com-

pression Algorithm. Software—Practice and Experi-

ence, 30(13):1465–1483, 2000.

P. Deutsch. DEFLATE Compressed Data Format Spec-

iﬁcation version 1.3. In http://www.ietf.org. IETF

RFC1951, 1996.

G.S. Fowler, A. Hume, D.G. Korn, and K.-P. Vo. Migrating

an MVS Mainframe Application to a PC. In Proceed-

ings of Usenix’2004. USENIX, 2004.

J. Gailly and M. Adler. Zlib, http://www.zlib.net. Technical

report, 2005.

D.A. Huffman. A Method for the Construction of

Minimum-Redundancy Codes. Proc. of the IRE,

40(9):1098–1101, Sept 1952.

J.J. Hunt, K.-P. Vo, and W.F. Tichy. Delta Algorithms: An

Empirical Analysis. ACM Transactions on Software

Engineering and Methodology, 7:192–214, 1998.

D.W. Jones. Practical Evaluation of a Data Compression

Algorithm. In Data Compression Conference. IEEE

Computer Society Press, 1991.

David G. Korn and Kiem-Phong Vo. SFIO: Safe/Fast

String/File IO. In Proc. of the Summer ’91 Usenix

Conference, pages 235–256. USENIX, 1991.

D.G. Korn, J. MacDonals, J. Mogul, and K.-P. Vo.

The VCDIFF Generic Differencing and Compres-

sion Data Format. Internet Engineering Task Force,

www.ietf.org, RFC 3284, 2002.

D.G. Korn and K.-P. Vo. Engineering a Differencing

and Compression Data Format. In Proceedings of

Usenix’2002. USENIX, 2002.

H. Liefke and D. Suciu. Xmill: an efﬁcient compressor for

xml data. In Proc. of SIGMOD, pages 153–164, 2000.

G. Manzini and M. Rastero. A Simple and Fast DNA Com-

pression Algorithm. Software—Practice and Experi-

ence, 34:1397–1411, 2004.

J. Seward. Bzip2, http://www.bzip.org. Technical report,

1994.

W. F. Tichy. RCS—a system for version control. Software—

Practice and Experience, 15(7):637–654, 1985.

B.D. Vo and K.-P. Vo. Using Column Dependency to Com-

press Tables. Data Compression Conference, 2004.

B.D. Vo and K.-P. Vo. Compressing Table Data with Col-

umn Dependency. Theoretical Computer Science, ac-

cepted for publication, 2006.

K.-P. Vo. The Discipline and Method Architecture for

Reusable Libraries. Software—Practice and Experi-

ence, 30:107–128, 2000.

I.H. Witten, M. Radford, and J.G. Cleary. Arithmetic

Coding for Data Compression. Comm. of the ACM,

30(6):520–540, June 1987.

J. Ziv and A. Lempel. A Universal Algorithm for Sequen-

tial Data Compression. IEEE Trans. on Information

Theory, 23(3):337–343, May 1977.

J. Ziv and A. Lempel. Compression of Individual Sequences

via Variable-Rate Coding. IEEE Trans. on Informa-

tion Theory, 24(5):530–536, 1978.

VCODEX: A DATA COMPRESSION PLATFORM