MULTI-CRITERION GENETIC PROGRAMMING WITH

NEGATIVE SELECTION FOR FINDING PARETO SOLUTIONS

Jerzy Marian Balicki

Naval University of Gdynia, Smidowicza Street, Gdynia, Poland

Keywords: Genetic programming, multi-criterion optimization, distributed systems.

Abstract: Multi-criterion genetic programming (MGP) is a rel

atively new approach for a decision making aid and it

can be applied to determine the Pareto solutions. This purpose can be obtained by formulation of a multi-

criterion optimization problem that can be solved by genetic programming. An improved negative selection

procedure to handle constraints in the MGP has been proposed. In the test instance, both a workload of

a bottleneck computer and the cost of system are minimized; in contrast, a reliability of the distributed

system is maximized.

1 INTRODUCTION

Genetic programming is a software technique for

getting computers to automatically solve a problem

(Koza, 1992). This approach starts from a high-level

statement of what needs to be done and

automatically creates a computer program. One of

the essential challenges of computer science is to get

a computer to solve a difficulty without explicitly

programming it to do so. Paraphrasing Arthur

Samuel – founder of the field of machine learning –

this challenge is “How can computers be made to do

what needs to be done, without being told exactly

how to do it?” (Samuel, 1960).

Genetic programming uses the Darwinian

pri

nciple of natural selection along with models of

crossover, mutation, and mechanisms of biology to

obtain a population of programs. Genetic

programming has been successfully applied to

a wide variety of problems from numerous different

fields (Koza et al., 2004).

Multi-criterion genetic programming (MGP) is

relatively new approach for a decision making aid

and it can be applied to determine the Pareto

solutions (Balicki, 2006). This purpose can be

obtained by formulation a multi objective

optimization problem that can be solved by adjusted

genetic programming.

In this paper, genetic programming paradigm is

mplemented as a genetic algorithm written in the

Matlab language. Chromosomes are generated as the

functions, and then genetic operators are applied for

finding functions that produce Pareto-suboptimal

solutions.

2 GENETIC PROGRAMMING

Genetic programming is an appealing paradigm of

an artificial intelligence (Koza et al., 2004).

Solutions to several problems have been found for

instances from different areas like optimal control,

planning and sequence induction. Genetic

programming permits finding solutions to symbolic

regression, automatic programming or discovering

a game playing strategy.

Furthermore, problems related to empirical

discoveri

ng and forecasting, symbolic integration or

differentiation, discovering mathematical identities

or classification and decision tree induction can be

solved by this approach. Evolution of emergent

behaviour and also automatic programming of

cellular automata are on the list of problems that

have been solved successfully.

Figure 1 shows an example of a tree of the

com

puter program performance. This tree

corresponds to the program written in the LISP

language, as follows:

(GT (* -1.5 x) (LOG y (SQRT y)))

Above program calculates both the value –1.5x

and log(

), and then compares –1.5x to

log(

). If –1.5x is greater than log(

), then

120

Marian Balicki J. (2007).

MULTI-CRITERION GENETIC PROGRAMMING WITH NEGATIVE SELECTION FOR FINDING PARETO SOLUTIONS.

In Proceedings of the Second International Conference on Software and Data Technologies - PL/DPS/KE/WsMUSE, pages 120-127

DOI: 10.5220/0001336201200127

 SciTePress

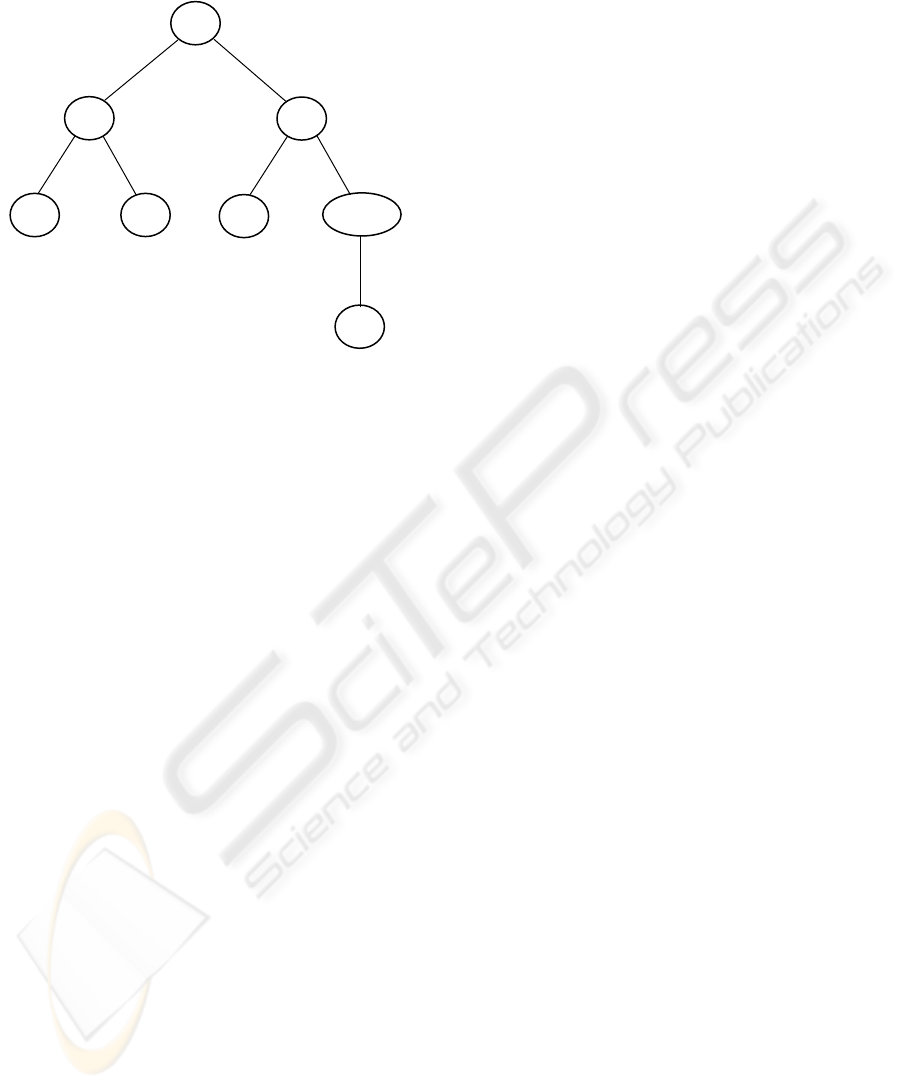
an outcome of the GT function is equal to 1.

However, in the other case, the result is –1.

Figure 1: Tree as a model of the computer program.

This tree is equivalent to the parse tree that most

compilers construct internally to represent the given

computer program. If a computer program was

represented by any algorithm form, genetic operators

like reproduction, crossover or mutation would be

complicated to implement.

A parse tree (a concrete syntax tree) is a tree that

represents the syntactic structure of a

string

according to some formal grammar. A program that

produces such trees is called a

parser. Parse trees

may be generated for

sentences in natural languages,

as well as during processing of computer languages,

such as programming languages.

A parse tree is made up of nodes and branches.

In a parse tree, each node is either a root node,

a branch node, or a leaf node.

Nodes can also be referred to as parent nodes

and child nodes. A parent node is one which has at

least one other node linked by a branch under it.

A child node is one which has at least one node

directly above it to which it is linked by a branch of

the tree.

Despite the data structure representing

chromosomes in an evolution strategy or an

evolutionary algorithm, a chromosome for genetic

programming is the tree of a computer program.

Even the simplest procedure differs from a complex

data structure, significantly. The procedure can

calculate what gives ability to represent not only

knowledge about a problem, but also it gives

possibility to draw conclusions. Moreover, it may

process data in the way difficult to discover. That is,

a computer program may model a solution to the

problem as an intelligent procedure.

Generation of the tree is an important step for

finding solutions. The size of the generated tree is

limited by the number of nodes or by the number of

the tree levels. Nodes in the tree are divided on

functional nodes and terminal ones. A functional

node represents the procedure randomly chosen

from the primary defined set of functions:

{

}

fff ,...,,...,

(1)

Each function should be able to accept, as its

arguments, any value and data type that may

possible be returned by the other procedure (Koza,

1992). Because a procedure is randomly chosen

from the set, and then it is returned, each function

should be able to accept, as its arguments, any value

and data type that may possible be returned by itself.

Moreover, each procedure should be able to accept

any value and data type that may possible be

assumed by any terminal in the terminal set:

{

}

aaa ,...,,...,

(2)

An above quality of procedure is called a closure

condition because each function should be well

defined and closed for any arrangement of

arguments that it may come across.

Another quality

, called the sufficiency condition,

requires that the solution to the problem should be

expressed by the combination of the procedures

from the set of functions and the arguments from the

set of terminals. For example, the set of functions

{

}

NOTORAND ,,

is sufficient to express any

Boolean function. If the logical operator AND is

removed from this set, the remaining procedure set

is still satisfactory for realizing any Boolean

function. A sufficient set is

{}

as well.

NOTAND ,

Let the following set of procedures be

considered for the problem of finding trajectory for

the underwater vehicle (Balicki, 2006):

{

}

/,-,*,,+

ENDE,MOVE,IF_IF_OBSTACLF

(3)

The procedure IF_OBSTACLE takes two

arguments. If the obstacle is recognized ahead the

underwater vehicle, the first argument is performed.

In the other case, the second argument is executed.

The function MOVE requires three arguments. It

causes the movement along the given direction with

the velocity equals the first argument during

assumed time Δt. The time Δt is the value that is

equal to the division a limited time by M

max

The direction of the movement is changed

according to the second and third arguments. The

second argument is the angle of changing this

direction up if it is positive or down if it is negative.

Similarly, the third argument represents an angle of

SQRT

LOG

-1.3

MULTI-CRITERION GENETIC PROGRAMMING WITH NEGATIVE SELECTION FOR FINDING PARETO

SOLUTIONS

121

changing the direction to the left if it is positive or

to the right if it is negative.

The last procedure IF_END ends the trajectory

of the underwater vehicle if it is in the destination

region or the expedition is continued if it is not

there. The set of arguments consists of the real

numbers generated from the interval (-1; 1).

A multi-criterion genetic algorithm has been

applied for operating on the population of the

computer procedures written in the Matlab language.

Numerical experiments confirm that feasible, sub-

optimal in Pareto sense, trajectories can be found by

genetic programming. Although, the quality of

obtained trajectories was a little lower than the

trajectories determined by an evolutionary algorithm

(Balicki, 2005), a paradigm of genetic programming

gives opportunity to solve that control problems for

changing environment.

3 NEGATIVE SELECTION

ALGORITHM

Multicriterion genetic programming is based on

using a genetic algorithm and to some extend it

inherits some disadvantiges of that approach. One of

them is the weak efficiency for finding the

admissinle solutions in optimization problems. To

improve this calculation situation, we propse the

development of the negative selection algorithm

from an immune systems.

The immune system can be seen as a distributed

adaptive system that is capable for learning, using

memory, and associative retrieval of information in

recognition (Jerne, 1984). Many local interactions

provide, in consequence, fault tolerance, dynamism

and adaptability.

The negative selection algorithm (NSA) for

detection of changes has been developed (Forest and

Perelson, 1991). This algorithm is based on the

discrimination principle that is used to know what is

a part of the immune system is.

Detectors are randomly generated to reduce

those detectors that are not capable of recognising

themselves. Subsequently, detectors proficient to

distinguish trespassers are kept. An adjusted

detection is performed probabilistically by the NSA

(Benaschi et al., 1999).

An antigen is a molecule that stimulates

a response against trespassers. The term originated

from the notion that they can stimulate antibody

generation. Moreover, the immune system consists

of some viruses as well as bacteria (Kim and

Bentley, 2002).

An antibody (an immunoglobulin) is a large

Y- shaped protein used to identify and neutralize

foreign objects like bacteria and viruses. The

antibody recognizes a specific target - an antigen.

The negative selection can be used to manage

constraints in an evolutionary algorithm by isolating

the contemporary population in two groups

(Wierzchon, 2005). Feasible solutions called

“antigens” create the first cluster, and the second

cluster of individuals consists of “antibodies” –

infeasible solutions. For that reason, the NSA is

applied to generate a set of detectors that verify the

state of constraints.

We assume the initial fitness for antibodies is

equal to zero. Then, a randomly chosen antigen G

is compared to the selected antibodies. After that,

the distance S between G

and the antibody B

calculated due to the amount of similarity at the

genotype level. The measure of genotype similarity

between the antigen and the antibody depends on

their representation. This assessment of similarity

for the integer version is, as follows (Balicki, 2005):

,),(

∑

−−−−

−=

BGBGS

(4)

where

;,1,position at antibody theof value

,,1,position at antigen theof value

solution, theoflength the

MmmB

MmmG

=−

−

The negative selection can be implemented by

a modified genetic algorithm. In that approach,

infeasible solutions that are similar to feasible ones

are preferred in the current population. Although,

almost all the random choices are based on the

uniform distribution, the pressure is directed to

improve the fitness of appropriate infeasible

solutions.

4 RANKING PROCEDURE FOR

NSA

The situation that the fitness of the winner is

increased by adding the magnitude of the similarity

measure may pass over a non-feasible solution with

the relatively small value of this assessment (1).

Nevertheless, some constraints may be satisfied by

this alternative.

What is more, if a constraint is exceeded and the

others are not, the value of a similarity measure may

be lower for some cases. The first of two similar

solutions, in genotype sense, may not satisfy this

constraint and the second one may satisfy it.

To avoid this limitation of the NSA, some

distance measures can be applied from the state of

ICSOFT 2007 - International Conference on Software and Data Technologies

122

an antibody to the state of the selected antigen,

according to the constraints.

Equalities and inequalities that are of interest to

us are, as follows:

,,1,0)( Kkxg

=≤

(5)

.,1,0)( Llxh

(6)

The distance measures from the state of an

antibody B

to the state of the selected antigen G

are defined, as below:

.,,1

,,,1,)(

,,,1),()(

),( LKNNn

lKnLlBh

knKkGgBg

GBf

+==

⎪

⎩

⎪

⎨

⎧

+==

==−

−

−−

(7)

The distance f

)

is supposed to be

minimized for all the constraint numbers n. If the

antibody B

is marked by the smaller assessment

)

to the antigen than the antibody C

, then

ought to be preferred to C

due to the

improvement of the nth constraint. Moreover, if the

antibody B

is characterized by all shorter distances

to the antigen than the antibody C

, then B

should

be preferred for all constraints.

However, some situations may occur when B

characterized by the shorter distances for some

constraints and the antibody C

is marked by the

shorter distances for the others. In this case, it is

difficult to select an antibody. We suggest

introducing a ranking procedure to calculate fitness

of antibodies and then to select the winner.

In the improved negative selection algorithm

with ranking procedure denoted as NSA*, distances

between the chosen antigen and some antibodies are

calculated. Afterwards, the nondominated antibodies

are determined according to their distances (7) to the

antigen, and then, they get the rank equal to 1. Next,

they are temporary eliminated from the subset of

antibodies. Subsequently, the new nondominated

antibodies are determined from the reduced subset

and they get the rank equal to 2. In this procedure,

that level is increased and it is repeated until the

subset of antibodies is exhausted. All the non-

dominated antibodies have the same fitness because

of the equivalent rank. The last market antibody gets

the rank equal to r

max

If B

is characterized by the rank r(B

), then

1 ≤ r(B

) ≤ r

max

and the increment of the fitness

function value is estimated, as below:

.1)()(

max

+−=Δ

−−

BrrBf

(8)

Afterwards, the fitness values of all selected

antibodies are increased by adding their assigned

increments. The antibodies are returned to the

current population and this process is repeated

typically three times the number of antibodies. Each

time, a randomly chosen antigen is compared to the

same subset of antibodies.

Afterwards, a new population is constructed by

reproduction, crossover and mutation without

calculations of fitness. That process is repeated until

a convergence of population emerges or until

a maximal number of iterations is exceeded. At the

end, the final population as outcomes from the

negative selection algorithm is returned to the

external evolutionary algorithm.

5 OPTIMIZATION OF

DISTRIBUTED SYSTEM

To test the ability of the MGP with NSA* for

handling constraints, we consider a multi-criterion

optimisation problem for task assignment in

a distributed computer system (Balicki, 2005).

Finding allocations of program modules may

decrease the total time of a program execution by

taking a benefit of the particular properties of some

workstations or an advantage of the computer load.

An adaptive evolutionary algorithm has been

considered for solving multi-objective optimisation

problems related to task assignment that minimize

max

– a workload of a bottleneck computer and C –

the cost of machines. The total numerical

performance of workstations is another criterion for

assessment the quality of a task assignment and it

has been involved to multi-criterion problem.

Moreover, a reliability R of the system is an

additional criterion that is important to assess the

quality of a task assignment.

In the considered problem, both a workload of

a bottleneck computer and the cost of machines are

minimized; in contrast, a reliability of the system is

maximized. In addition, constraints related to

memory limits and computer locations are imposed

on the feasible task assignment. A set of program

modules {M

,...,M

www

} communicated to each

others is considered among the coherent computer

network with computers located at the processing

nodes from the set

1 Ii

W },...,,...,{

. A set of

program modules is mapped into the set of parallel

performing tasks {T

,...,T

}. Some task

scheduling algorithms based on tabu search are

proposed in (Weglarz et al., 2003).

Let the task T

be executed on some computers

taken from the set of available computer sorts

},...,,...,{

1 Jj

. The overhead performing

time of the task T

by the computer

is represented

by an item .

MULTI-CRITERION GENETIC PROGRAMMING WITH NEGATIVE SELECTION FOR FINDING PARETO

SOLUTIONS

123

Let

be failed independently due to an

exponential distribution with rate

. We do not

take into account of repair and recovery times for

failed computer in assessing the logical correctness

of an allocation. Instead, we shall allocate tasks to

computers on which failures are least likely to occur

during the execution of tasks. Computers and tasks

can be allocated to nodes in purpose to maximize the

reliability function R defined, as below (Balicki,

2005):

),exp()(

11 1

∏∏∏

== =

−=

vivjj

xxtxR

(9)

where

⎩

⎨

⎧

, the toassigned is if1

case.other thein0

⎩

⎨

⎧

, toassigned is taskif1

case,other thein0

.],...,,...,,,...,,...,[

1111

IJij

xxxxxxx

πππ

A computer with the heaviest task load is the

bottleneck machine and its workload is a critical

value that is supposed to be minimized. The

workload Z

max

(x) of the bottleneck computer for the

allocation x is provided by the subsequent formula:

,max)(

111 111

max

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

∑∑∑∑∑∑

≠≠

∈

vuikij

xxxxtxZ

(10)

where

vuik

– the total communication time between

the task T

assigned to the ith node and the T

assigned to the kth node.

Figure 2 shows the workload of the bottleneck

computer in the distributed computer system for

generated task assignments in a systematic way. The

function Z

max

takes value from the period [40; 110]

for 256 solutions. What is more, even a small change

in task assignment related to the movement of a task

to another computer or a substitution of computer

sort can cause a relatively big alteration of its

workload.

A computer is supposed to be equipped with

necessary capacities of resources. Let the following

memories z

,...,z

be available in the distributed

system and let d

be the capacity of memory z

in the

workstation

. We assume the task T

reserves c

units of memory z

and holds it during a program

execution. The memory limit in a machine cannot be

exceeded in the ith node, what is written, as bellows:

.,1,,1,

RrIixdxc

ijjr

vivr

==≤

∑∑

(11)

Measure of the task assignment is a cost of

computers:

xκxC

∑∑

=)(

(12)

where

corresponds to the cost of the computer

100

150 200 250 300

100

110

max

[TU]

Number of solution

Figure 2: Workload of the bottleneck computer

for generated solutions.

6 ADAPTIVE EVOLUTIONARY

ALGORITHM

The total computer cost is in conflict with the

numerical performance of a distributed system,

because the cost of a computer usually depends on

the quality of its components. The faster computer or

the higher reliability of it is, the more expensive it is.

Additionally, the workload of the bottleneck

computer is in conflict with the cost of the system.

Let (X, F, P) be the multi-criterion optimisation

question for finding the representation of Pareto-

optimal solutions (Coello Coello et al., 2002). It is

established, as follows:

1) X - an admissible solution set

)( JVI

∈= BX

;,1,,1,

RrIixdxc

ijjr

vivr

==≤

∑∑

ICSOFT 2007 - International Conference on Software and Data Technologies

124

;,1 ,1

Vvx

∑

},1,1

Iix

∑

where B

= {0, 1}

2) F - a quality vector criterion

: RX →F

(13)

where

– the set of real numbers,

F(x) = [–R(x), Z

max

(x), C(x)]

for x∈X,

R(x), Z

max

(x), F

(x) are calculated by (9), (10)

and (12), respectively

3) P - the Pareto relation (Deb, 2001).

An analysis of the task assignments has been

carried out for two genetic approaches (Zitzler et al.,

2000). The first one was an adaptive multi-criterion

evolutionary algorithm with tabu mutation AMEA*

(Balicki, 2005). Tabu search procedure was applied

as an additional mutation operator to decrease the

workload of the bottleneck computer. Moreover, we

suggest introducing a negative selection algorithm

with ranking procedure to improve the quality of

obtained solutions.

Better outcomes from the NSA* are transformed

into improving of solution quality obtained by the

adaptive multi-criterion evolutionary algorithm with

tabu mutation AMEA*. This approach gave better

results than the previous version of that algorithm

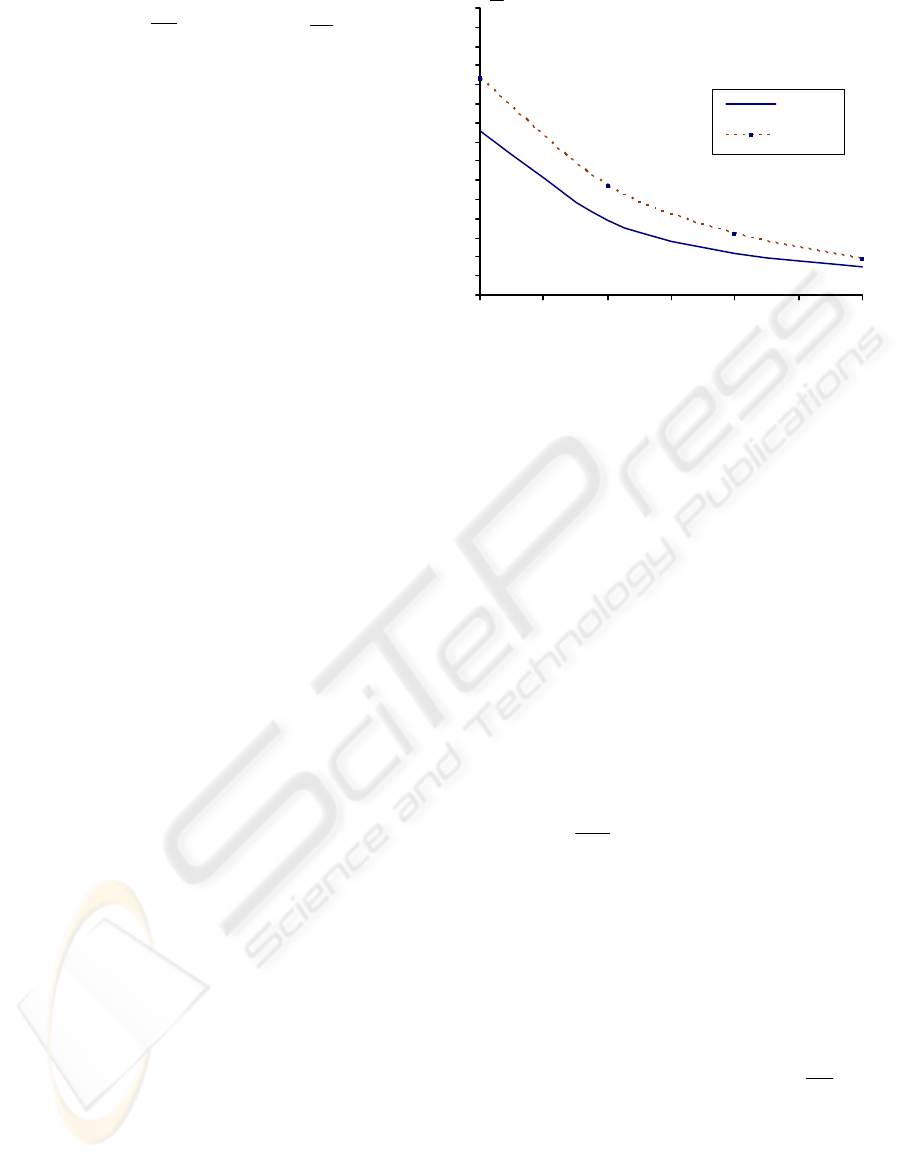
named AMEA+. After 200 generations, an average

level of Pareto set obtaining was 1.5% for the

AMEA*, 1.9% for the AMEA+ (Figure 3).

Fifty test preliminary populations were prepared,

and each algorithm started from these solutions. For

integer constrained coding of chromosomes there

were 12 decision variables in the test optimisation

problem. The binary search space consisted of

1.0737

chromosomes and included 25 600

admissible solutions.

7 MULTI-CRITERION GENETIC

PROGRAMMING

Genetic programming paradigm can be implemented

as a genetic algorithm written in the Matlab

language. Chromosomes are generated as the Matlab

functions and then genetic operators are applied for

finding Pareto-suboptimal solutions. Results may be

compared with outcomes obtained by AMEA*.

1,5

8,6

3,9

1,9

5,7

11,3

50 75 100 125 150 175 200

AMEA*

AMEA+

[%]

Generation number

Figure 3: Outcome convergence for AMEAs.

Figure 4 shows a scheme of the MGP that

operates on the population of program functions.

The preliminary population of programs is created in

a specific manner (Fig. 4, line 3). Each generated

program consists of set of procedures and set of

attributes. Set of procedures is defined, as follows:

{

}

/,-,*,,

listF

(14)

where

list – the procedure that convert I(V+J) input real

numbers called activation levels on I(V+J) output

binary numbers

ππππ

IJijJ

xxxxxxxx ,...,,...,,...,,,...,,...,,...,

111111

The procedure list is obligatory the root of the

program tree and appears only one in a generated

program. In that way, the formal constraint

Mmx

,1, =∈ B

is satisfied. An activation level

is supplied to a root from the sub-tree that is

randomly generated with using arithmetic operators

{+, -, *, /} and the set of terminals.

Let be the set of numbers that consists of

the given data for the instance. A terminal set is

determined for the problem, as below:

,LDT ∪

(15)

where

–

set of n random numbers,

.D=n

If x calculated by the program is admissible, then

the fitness function value (Fig. 4, line 4) is

estimated, as below:

,1)()(

maxmax

−

Pxrrxf

(16)

MULTI-CRITERION GENETIC PROGRAMMING WITH NEGATIVE SELECTION FOR FINDING PARETO

SOLUTIONS

125

where r(x) denotes the rank of an admissible

solution,

)(1

max

rxr ≤≤

Figure 4: Multi-criterion genetic programming MGP*.

Another ranking procedure assigns each

individual a rank based on the number of other

individuals by which it is dominated (Fonseca and

Fleming, 1995). A niching procedure modifies it.

The surface region of the Pareto front is divided by

the size of the population. The number of other

member’s falling within the sub-area of any

individual is taken to establish the penalty for it.

In the two-weight tournament selection (Fig. 4,

line 12), the roulette rule is carried out twice. If two

potential parents (a, b) are admissible, then

a dominated one is eliminated. If two solutions non-

dominate each other, then they are accepted. If

potential parents (a, b) are non-admissible, then an

alternative with the smaller penalty is selected.

The fitness sharing technique can be substituted

by the adaptive changing of main parameters. The

quality of attained solutions increases in

optimisation problems with one criterion, if the

crossover probability and the mutation rate are

changed in an adaptive way (Sheble and Britting,

1995). The crossover point is randomly chosen for

the chromosome X in the S-crossover operator (Fig.

4, line 13). The crossover probability is 1 at the

initial population and each pair of potential parents

is obligatory taken for the crossover procedure.

A crossover operation supports the finding of

a high-quality solution area in the search space. It is

important in the early search stage. If the number of

generation t increases, the crossover probability

decreases according to the formula

max

/Tt

−

1. BEGIN

2. t:=0, set the even size of population L, p

:=1/(ML)

3. generate initial population of programs P(t)

4. run programs, calculate ranks r(x) and fitness

)(),( txxf P∈

The search region or some search areas are

identified after several crossover operations on

parent pairs. That is why, value p

is smaller and it is

equal to 0.6065, if t

=100 for maximum number of

population T

max

=200. The final smallest value p

0.3679. A crossover probability decreases from 1 to

exp(-1), exponentially. During S-crossover, a subtree

with the randomly selected root from program a is

exchanged with another subtree from tree b.

5. finish:=FALSE

6. WHILE NOT finish DO

7. BEGIN /* new population */

8. t:= t+1,

∅=:)(tP

calculate selection

probabilities

)

(xp

)1(

−

∈ tPx

10. FOR L/2 DO

11. BEGIN /* reproduction cycle */

12. 2WT-selection of a potential parent pair (

a,b)

from the population

P(t-1)

In S-mutation (Fig. 4, line 14), the random node

is chosen, the related subtree is removed, and then

a new subtree is generated. A mutation rate is

constant in the MGP and it is equal to 1/M, where M

represents the number of decision variables.

13. S-crossover of a parent pair (

a,b) with the

adaptive crossover rate p

max

−

14. S-mutation of an offspring pair (

a',b') with the

mutation rate p

15. P(t):=P(t)∪(a',b'}

16. END

8 NUMERICAL EXPERIMENTS

17.

calculate ranks r(x) and fitness

)(),( txxf P∈

18. IF (P(t) converges OR t ≥ T

max

) THEN

finish:=TRUE

Better outcomes from the NSA* are transformed

into improving of solution quality obtained by the

MGP*. This approach gives similar results than the

AMEA*. After 200 generations, an average level of

Pareto set obtaining is 1.3% for the MGP*, 1.5% for

the AMEA*. All points have been found by MGP*

for that instance.

19. END

20. END

For the other instance with 15 tasks, 4 nodes, and

5 computer sorts, there are 80 binary decision

variables. An average level of convergence to the

Pareto set is 17.7% for the MGP* and 17.4% for the

AMEA*. A maximal level is 28.5% for the MGP*

and 29.6% for the AMEA*. For this instance the

average number of optimal solutions is 19.5% for

the MGP* and 21.1% for the AMEA*.

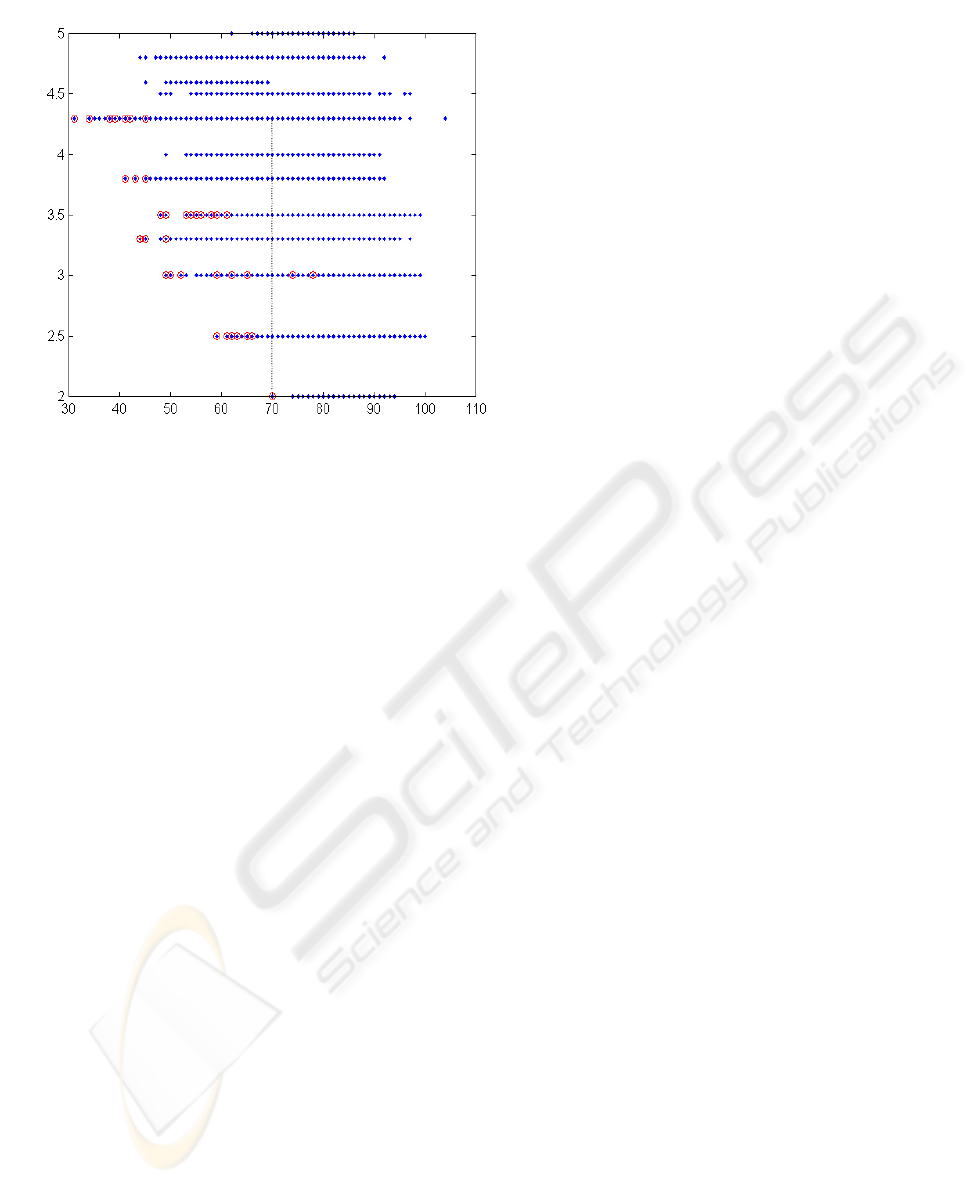
Figure 5 shows the process of finding efficient

task assignment by MGP* for the cut obtained from

the evaluation space according to the cost criterion C

and the workload of the bottleneck computer Z

max

ICSOFT 2007 - International Conference on Software and Data Technologies

126

[MU]

max

[ TU ]

Figure 5: Pareto front and results from GMP*.

An average level of convergence to the Pareto

set, an maximal level, and the average number of

optimal solutions become worse, when the number

of task, number of nodes, and number of computer

types increase. An average level is 37.7% for the

MGP* versus 35,7% for the AMEA*, if the instance

includes 50 tasks, 4 nodes, 5 computer types and

also 220 binary decision variables.

9 CONCLUDING REMARKS

Genetic programming is relatively new paradigm of

artificial intelligence that can be used for finding

Pareto-optimal solutions. A computer program as

a chromosome is a subject of genetic operators such

as recombination, crossover and mutation. It gives

possibility to represent knowledge that is specific to

the problem in more intelligent way than for the data

structure. A genetic algorithm has been applied for

operating on the population of the computer

procedures written in the Matlab language.

Initial numerical experiments confirm that

feasible, sub-optimal in Pareto sense, task

assignments can be found by genetic programming.

That approach permits for obtaining comparable

quality outcomes to advanced evolutionary

algorithm.

Our future works will focus on testing the other

sets of procedures and terminals to find the Pareto-

optimal task assignments for different criteria and

constraints.

REFERENCES

Balicki, J., 2006. Multicriterion Genetic Programming for

Trajectory Planning of Underwater Vehicle. Int.

Journal of Computer Science and Network Security,

Vol. 6, No. 12, December 30, 1-6.

Balicki, J., 2005. Immune Systems in Multi-criterion

Evolutionary Algorithm for Task Assignments in

Distributed Computer System. Lectures Notes in

Computer Science, Vol. 3528, 51-56.

Bernaschi, M., Castiglione, F., Succi, S., 2006. A High

Performance Simulator of the Immune System. Future

Generation Computer System, Vol. 15, 333-342.

Coello Coello, C. A., Van Veldhuizen, D. A., Lamont,

G.B., 2002.

Evolutionary Algorithms for Solving

Multi-Objective Problems

. Kluwer Academic

Publishers, New York.

Deb, K., 2001.

Multi-Objective Optimization using

Evolutionary Algorithms

, John Wiley & Sons,

Chichester.

Fonseca, C. M., Fleming, P. J., 1995. An Overview of

Evolutionary Algorithms in Multiobjective

Optimisation, Evolutionary Computation, Vol. 3, No.

1, 1-16.

Forrest, S., Perelson, A.S., 1991, Genetic Algorithms and

the Immune System. Lecture Notes in Computer

Science, 320-325.

Jerne, N.K., 1984. Idiotypic Networks and Other

Preconceived Ideas. Immunological Revue, Vol. 79,

5-25.

Kim, J. and Bentley, P. J., 2002.

Immune Memory in the

Dynamic Clonal Selection Algorithm.

Proc. of the First

Int. Conf. on Artificial Immune Systems, Canterbury,

57-65.

Koza J.R., Keane M. A., Streeter M. J., Mydlowec W. ,

Yu J., and Lanza G., 2003. Genetic programming IV.

Routine Human-Competitive Machine Intelligence.

Kluwer Academic Publishers, New York.

Koza, J. R., 1992. Genetic Programming: On the

Programming of Computers by Means of Natural

Selection. Cambridge, MA: The MIT Press.

Samuel A. L., 1960. Programming Computers to Play

Games.

Advances in Computers 1: 165-192.

Sheble, G. B., Britting, K., 1995. Refined Genetic

Algorithm – Economic Dispatch Example. IEEE

Transactions on Power Systems, Vol. 10, No. 2, 117-

124.

Weglarz, J., Nabrzyski, J., Schopf, J., 2003, Grid Resource

Management: State of the Art and Future Trends.

Kluwer Academic Publishers, Boston.

Wierzchon, S. T., 2005. Immune-based Recommender

System. In O. Hryniewicz, J. Kacprzyk, J. Koronacki

and S. T. Wierzchon (eds.) Issues in Intelligent

Systems. Paradigms. Exit, Warsaw, 341-356.

Zitzler, E., Deb, K., and Thiele, L., 2000. Comparison of

Multiobjective Evolutionary Algorithms: Empirical

Results. Evolutionary Computation, Vol. 8, No. 2 173-

195.

MULTI-CRITERION GENETIC PROGRAMMING WITH NEGATIVE SELECTION FOR FINDING PARETO

SOLUTIONS

127