A LANGUAGE FOR SPECIFYING INFORMATIONAL GRAPHICS
FROM FIRST PRINCIPLES
Stuart M. Shieber
Division of Engineering and Applied Sciences, Harvard University, Cambridge, MA, USA
Wendy Lucas
Computer Information Systems Department, Bentley College, Waltham, MA, USA
Keywords:
Visualization language, information visualization, graph specification, charting.
Abstract:
Information visualization tools, such as commercial charting packages, provide a standard set of visualizations
for tabular data, including bar charts, scatter plots, pie charts, and the like. For some combinations of data and
task, these are suitable visualizations. For others, however, novel visualizations over multiple variables would
be preferred but are unavailable in the fixed list of standard options. To allow for these cases, we introduce
a declarative language for specifying visualizations on the basis of the first principles on which (a subset
of) informational graphics are built. The functionality we aim to provide with this language is presented by
way of example, from simple scatter plots to versions of two quite famous visualizations: Minard’s depiction
of troop strength during Napoleon’s march on Moscow and a map of the early ARPAnet from the ancient
history of the Internet. Benefits of our approach include flexibility and expressiveness for specifying a range
of visualizations that cannot be rendered with standard commercial systems.
1 INTRODUCTION
Standard information-visualization tools provide a
predefined set of visualizations for representing tab-
ular, primarily numeric, data. While representations
such as bar charts and pie charts may be well-suited
for certain data visualization needs, they are unable
to represent more complex relationships involving
multiple variables. Representations of network ac-
tivity or business performance measures, for exam-
ple, can benefit from novel visualizations over mul-
tiple variables, which are unavailable in commercial
charting packages. Indeed, quite famous visualiza-
tions like Minard’s depiction of troop strength dur-
ing Napoleon’s march on Moscow or the maps of the
early ARPAnet from the ancient history of the Inter-
net
1
are well out of the scope of standard visualiza-
tion packages, despite the fact that they are built on
the basis of the same first principles from which more
standard visualizations are derived.
To allow for such visualizations, we introduce a
language for specifying informational graphics from
1
See Figures 3 and 6 for our versions of these visualiza-
tions.
first principles. One can view the goal of the present
research as doing for information visualization what
spreadsheet software did for business applications.
Prior to Bricklin’s VisiCalc, business applications
were built separately from scratch. By identifying the
first principles on which many of these applications
were built — namely, arithmetic calculations over ge-
ographically defined values — the spreadsheet pro-
gram made it possible for end users to generate their
own novel business applications. This flexibility was
obtained at the cost of requiring a more sophisticated
user, but the additional layer of complexity can be
hidden from naive users through prepackaged spread-
sheets.
Similarly, we propose to allow direct access to the
first principles on which (a subset of) informational
graphics are built through an appropriate specifica-
tion language. The advantages are again flexibility
and expressiveness, with the same cost in terms of
user sophistication and mitigation of this cost through
prepackaging.
For expository reasons, the functionality that we
aim for is first presented by way of example. We hope
that the reader can easily extrapolate from the pro-
5
M. Shieber S. and Lucas W. (2007).
A LANGUAGE FOR SPECIFYING INFORMATIONAL GRAPHICS FROM FIRST PRINCIPLES.
In Proceedings of the Second International Conference on Software and Data Technologies - PL/DPS/KE/WsMUSE, pages 5-12
DOI: 10.5220/0001326300050012
Copyright
c
 SciTePress

vided examples to see the power of the language. We
then describe the primary constructs in the language
and the output generation process for our implemen-
tation, which was used to generate the graphics shown
in this paper. Some aspects of the language have not
yet been implemented (in particular, constraints other
than equality), but are described so as to provide a
fuller picture of the potential scope of visualizations
that can be generated in this way.
2 THE STRUCTURE OF
INFORMATIONAL GRAPHICS
In order to define a language for specifying informa-
tional graphics from first principles, those principles
must be identified. For the subset of informational
graphics that we consider here, the underlying princi-
ples are relatively simple:
• Graphics are constructed based on the rendering
of generic graphical objects taken from a small
fixed set (points, lines, polygons, text, etc.).
• The graphical properties of these generic graphi-
cal objects are instantiated by being tied to values
taken from the underlying data (perhaps by way
of computation).
• The relationship between a data value and a
graphical value is mediated by a function called
a scale.
• Scales can be depicted via generic graphical ob-
jects referred to as legends. (A special case is an
axis, which is the legend for a location scale.)
• The tying of values is done by simple constraints,
typically of equality, but occasionally of other
types.
For example, consider a generic graphical object,
the point, which has graphical properties like hori-
zontal and vertical position, color, size, and shape.
The standard scatter plot is a graphic where a single
generic object, a point, is instantiated in the following
way. Its horizontal and vertical position are directly
tied by an equality constraint to values from particular
data fields of the underlying table. The other graph-
ical properties may be given fixed (default) values or
tied to other data fields. In addition, it is typical to
render the scales that govern the mapping from data
values to graphical locations using axes.
Suppose we have a table Table with fields f, g,
and h as in Table 1(a). We can specify a scatter plot of
the first two fields in just the way that was informally
described above:
Table 1: Tables providing underlying data for the sample
scatter plots (a) and the scatter plot of scatter plots (b).
f g h
80 80 0
60 120 10
100 60 5
v1 v2 v3 v4
15 12 3 4
15 12 5 8
15 12 7 10
12 20 1 10
12 20 9 5
12 20 11 12
20 12 5 5
20 12 13 19
20 17 4 7
20 17 8 1
20 17 12 19
(a) (b)
(a) (b)
(c) (d)
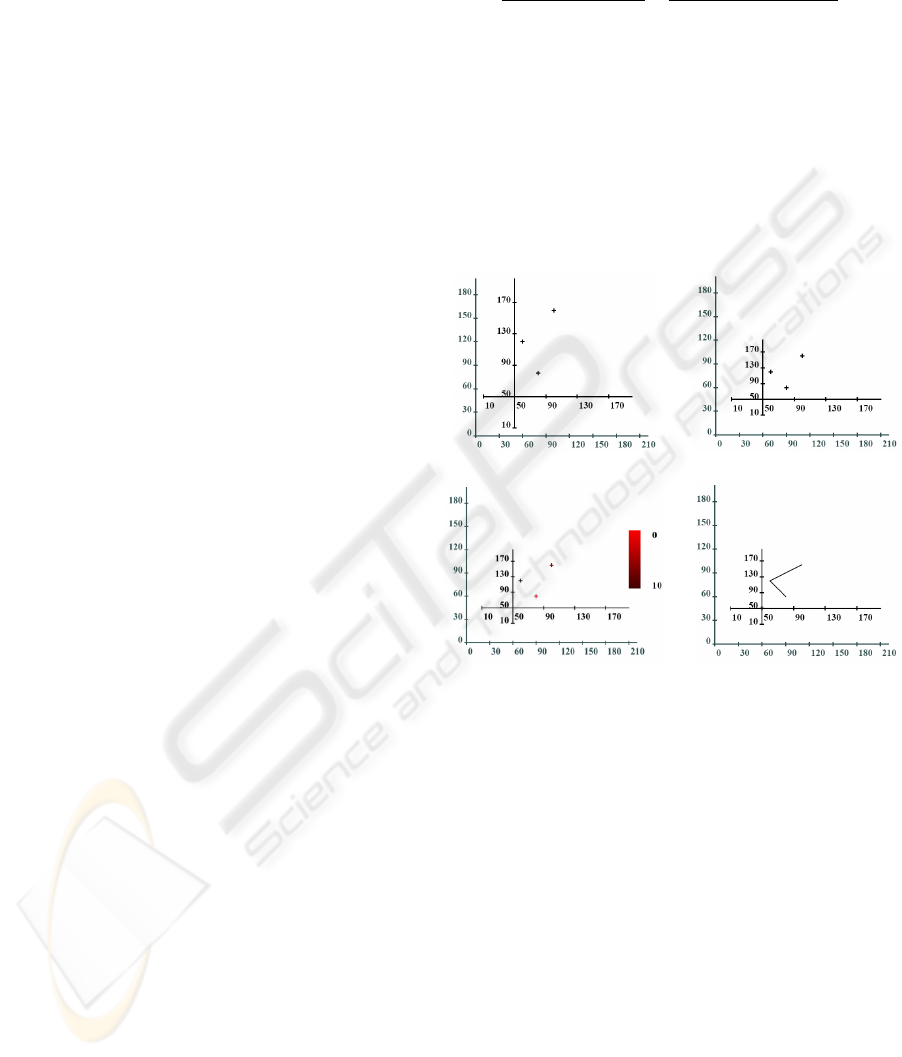
Figure 1: Some simple graphs defined from first principles.
{make p:point with
p.location = Canvas(record.f, record.g)
| record in SQL("select f, g from Table1")};
make a:axis with
a.aorigin = (50,50),
a.ll = (10,10),
a.ur = (200,200),
a.tick = (40,40);
The make keyword instantiates a generic graphical
object (point) and sets its attributes. The set com-
prehension construct ({·|·}) constructs a set with ele-
ments specified in its first part generated with values
specified in its second part. Finally, we avail ourselves
of a built-in scale, Canvas, which maps numeric val-
ues onto the final rendering canvas. One can think of
this as the assignment of numbers to actual pixel val-
ues on the canvas. A depiction of the resulting graphic
is given in Figure 1(a). (For reference, we show in
light gray an extra axis depicting the canvas itself.)
ICSOFT 2007 - International Conference on Software and Data Technologies
6

In general, some scaling of the data might be use-
ful. We define a 2-D Cartesian frame to provide this
scaling, using it instead of the canvas for placing the
points (Figure 1(b)).
let frame:twodcart with
frame.map(x,y) = Canvas(x + 10, y/2 + 20)
in
{make p:point with
p.location = frame.map(record.f, record.g)
| record in SQL("select f, g from Table1")},
make a:axis with
a.scale = frame.map,
a.aorigin = (50,50),
a.ll = (0, 0),
a.ur = (200,200),
a.tick = (50,50);
Other graphical properties of the point can be tied
to other fields. Here, we use a colorscale, a primi-
tive for building linearly interpolated color scales. A
legend for the color scale is positioned on the canvas
as well. (See Figure 1(c).)
let frame:twodcart with
frame.map(x,y) = Canvas(x + 10, y/2 + 20)
in
let color:colorscale with
color.min = ColorMap("red"),
color.max = ColorMap("black"),
color.minval = 0,
color.maxval = 10
in
{make p:point with
p.location = frame.map(rec.f, rec.g),
p.color = color.scale(rec.h)
|rec in SQL("select f, g, h from Table1")},
make a:axis with
a.scale = frame.map,
a.aorigin = (50,50),
a.ll = (0,0),
a.ur = (200,200),
a.tick = (50,50),
make c:legend with
c.scale = color,
c.location = frame.map(200, 250);
The ability to add other types of constraints dra-
matically increases the flexibility of the system. For
instance, stating that two values are approximately
equal (˜), instead of strictly equal (=), allows for ap-
proximate satisfaction of equality constraints. Fur-
ther, constraints of non-overlapping (no) force values
apart. Together, these constraints allow dither to be
added to scatter plots.
let frame:twodcart with
frame.map(x,y) = Canvas(x/2+1, y)
in
let points = {make p:point with
p.location ˜ frame.map(record.f, record.g)
| record in SQL("select f, g from Table1")}
in
no(points),
make a:axis with
a.scale = frame.map,
a.aorigin = (50,50),
a.ll = (0,0),
a.ur = (200,200),
a.tick = (50,50);
(Although this functionality is not available in the
currently implemented system, the basis for its imple-
mentation has been provided in earlier work on net-
work diagram layout (Ryall et al., 1997).)
A line chart can be generated using a line object
instead of a point object. Suppose we take the records
in Table 1(a) to be ordered, so that the lines should
connect the points from the table in that order. Then a
simple self-join provides the start points (x
1
, y
1
) and
end points (x
2
, y
2
) for the lines. By specifying the ap-
propriate query in SQL, we can build a line plot. The
specification language also allows definitions of more
abstract notions such as complex objects or group-
ings. We can use this facility to define line charts as
an object that can be instantiated with the given data
and frame:
define lchart:linechart with
let frame:twodcart with
frame.map = lchart.map
in
{make l:line with
l.start = frame.map(record.x1, record.y1),
l.end = frame.map(record.x2, record.y2)
| record in lchart.recs}
in
make l:linechart with
l.map(x,y) = Canvas(x + 10, y/2 + 20),
l.recs = SQL("select tab1.f as x1,
tab1.g as y1, tab2.f as x2,
tab2.g as y2
from Table1 as tab1,Table1 as tab2
where tab2.recno = tab1.recno+1"),
make a:axis with
a.scale = l.map,
a.aorigin = (50,50),
a.ll = (0, 0),
a.ur = (200,200),
a.tick = (50,50);
All objects share this ability to have their graph-
ical properties instantiated with specified data. This
allows generated visualizations themselves, such as
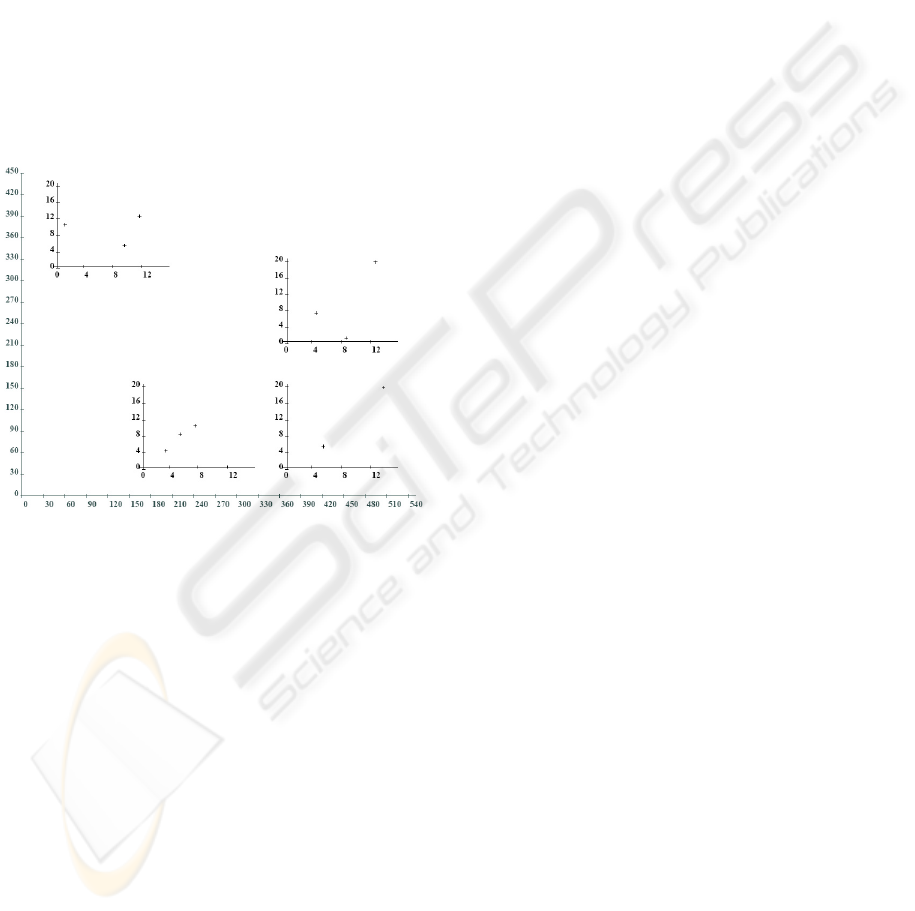
scatter plots, to be manipulated as graphical objects.
For instance, it is possible to form a scatter plot of
scatter plots. Figure 2 depicts such a graphic, as gen-
erated by the following specification and using the
data found in Table 1(b).
define s:splot with
let frame:twodcart with frame.map = s.map
in
{make p:point with
p.location = frame.map(rec.x, rec.y)
| rec in s.recs},
make a:axis with
a.scale = frame.map,
a.aorigin = s.aorigin,
a.ll = s.ll,
A LANGUAGE FOR SPECIFYING INFORMATIONAL GRAPHICS FROM FIRST PRINCIPLES
7

a.ur = s.ur,
a.tick = (4,4)
in
let outer:twodcart with
outer.map(x,y) = Canvas(40*x-430, 35*y-380)
in
let FrameRecs = SQL("select distinct
v1, v2 from matrix")
in
{make sp:splot with
sp.map(x,y) = outer.map(0.26*x +
framerec.v1, 0.167*y + framerec.v2),
sp.recs =
SQL("select v3 as x,v4 as y from matrix
where v1=framerec.v1
and v2=framerec.v2"),
sp.aorigin = (0,0),
sp.ll = (-.5,-.5),
sp.ur = (15,20)
| framerec in FrameRecs};
Figure 2: A scatter plot of scatter plots.
3 A DETAILED EXAMPLE: THE
MINARD GRAPHIC
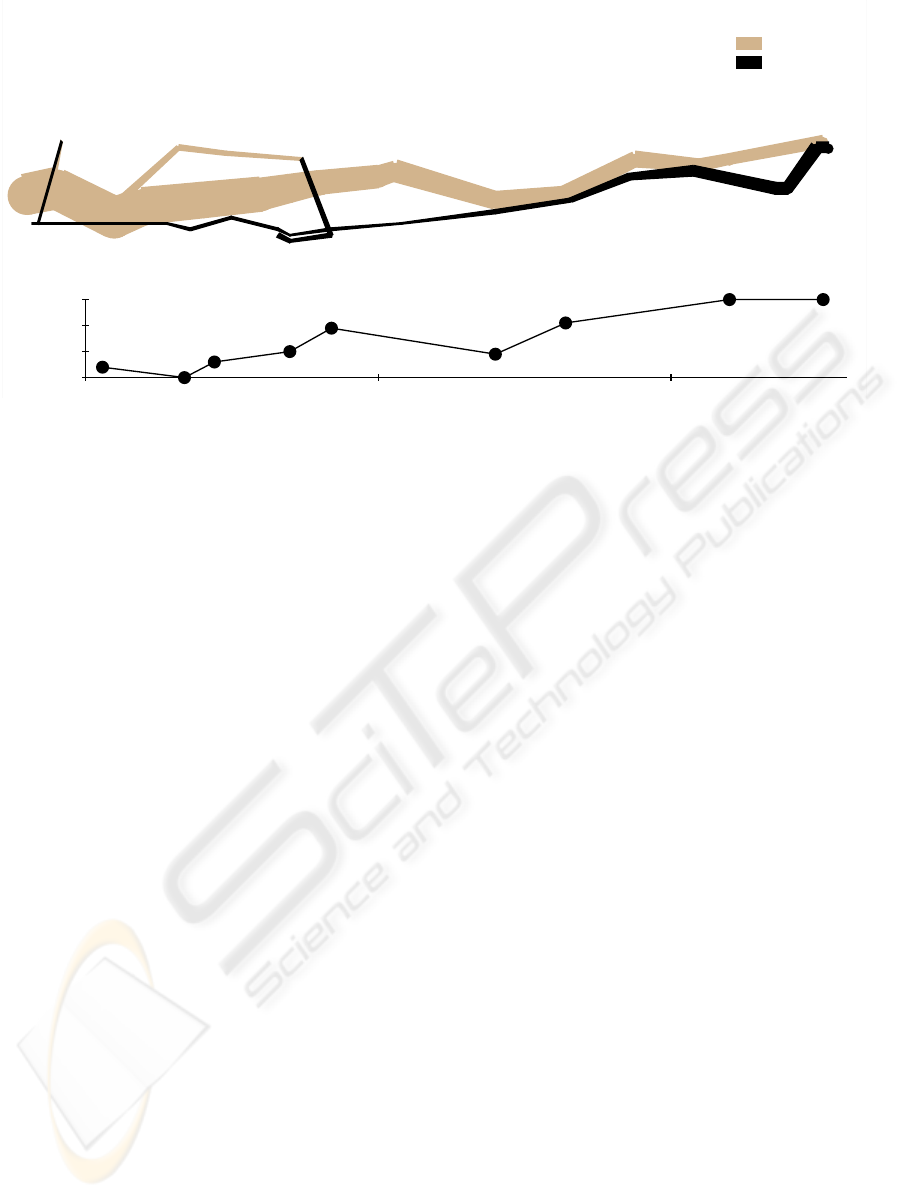
As evidence of the flexibility of this language, we de-
scribe its use for specifying Minard’s well known de-
piction of troop strength during Napoleon’s march on
Moscow. This graphic uses approximate geography
to show the route of troop movements with line seg-
ments for the legs of the journey. Width of the lines
is used for troop strength and color depicts direction.
A parallel graphic shows temperature during the in-
bound portion of the route, again as a line chart. Our
version of the graph is provided in Figure 3.
To generate this graphic, we require appropriate
data tables: marchNap includes latitude and longitude
at each way point, along with location name, direc-
tion, and troop strength; marchTemp includes latitude,
longitude, and temperature for a subset of the inbound
journey points, and marchCity provides latitude, lon-
gitude, and name for the traversed cities.
The main portion of the graphic is essentially a set
of line plots, one for each branch of the march, where
a branch is defined as a route taken in a single direc-
tion by a single division. Additional graphical prop-
erties (width and color) are tied to appropriate data
fields. Textual labels for the cities are added using
a text graphic object. A longitudinally aligned graph
presents temperature on the main return branch.
The specification for this graphic (sans the tem-
perature portion) is provided in Figure 4. After spec-
ifying some constants (lines 1–2), we define the de-
piction of a single branch of the march (6–16): a
mapping (m.map) specifies a Cartesian frame (7–8)
in which a line plot composed of a set of line seg-
ments (10–16) is placed, with one segment for each
set of records (16). These records provide start and
end points, along with widths at start and end (to be
interpolated between), and color (11–15).
Thus, to depict a march leg, all that must be pro-
vided is the mapping and the set of records. These are
constructed in lines 19–34. For each distinct direction
and division (19), a separate march leg depiction is
constructed (22–34). The mapping is a scaling of the
Canvas frame (23), with records for the appropriate
division and direction extracted from the marchNap
database (24–34). Finally, the cities are labeled using
the information in the marchCity database by tying
coordinates of text labels to an offset of the latitude
and longitude and setting a fixed color (37–42).
4 THE LANGUAGE
The examples from this paper were all generated from
an implementation of our language. The implementa-
tion techniques are outlined in Section 5. The under-
lying ideas could, however, be implemented in other
ways, for instance as a library of functions in a suit-
able functional language such as Haskell or ML.
The language is built around the specification of
objects. The main construct is objspec, with a pro-
gram defined as one or more objspecs. Objspecs are
used for instantiating a graphical object of a prede-
fined type, specifying relationships between the set of
actual data values and their graphical representations,
and defining new graphic types.
The make statement is used for instantiating a
new instance of an existing object type (either built-
in, such as point or line, or user-defined, such
as march) with one or more conditions. There are
two types of predefined objects: generic and scale.
Generic objects provide visual representations of data
ICSOFT 2007 - International Conference on Software and Data Technologies
8

Oct 18Oct 24
Nov 9
Nov 14
Nov 28
Dec 1
Dec 6
Dec 7
Kowno
Wilna
Smorgoni
Molodexno
Gloubokoe
Minsk
Studienska
Polotzk
Bobr
Witebsk
Orscha
Mohilow
Smolensk
Dorogobouge
Wixma
Chjat Mojaisk
Moscou
Tarantino
Malo-jarosewli
Advance
Retreat
Temperature
25 30 35
-30
-20
-10
0
Figure 3: The graphic generated by a specification extended from that of Figure 4, depicting the troop strength during
Napoleon’s march on Moscow.
1 let scalefactor = 45 in
let weight = .000002 in
% Define the depiction of one (multi-leg) branch of the march identified
5 % by a distinct direction and division
define m:march with
let frame:twodcart with
frame.map = m.map
in
10 {make l:line with
l.start = frame.map(rec.cx1, rec.cy1),
l.end = frame.map(rec.cx2, rec.cy2),
l.startWidth = scalefactor * weight * rec.r1,
l.endWidth = scalefactor * weight * rec.r2,
15 l.color = ColorMap(rec.color)
| rec in m.recs}
in
% Extract the set of branches that make up the full march
let FrameRecs = SQL("select distinct direct, division from marchNap")
20 in
% For each branch, depict it
{make mp:march with
mp.map(x,y) = Canvas(scalefactor*x - 1075, scalefactor*y - 2250),
mp.recs = SQL("select marchNap1.lonp as cx1, marchNap1.latp as cy1,
25 marchNap2.lonp as cx2, marchNap2.latp as cy2,
marchNap1.surviv as r1, marchNap2.surviv as r2,
marchNap1.color as color
from marchNap as marchNap1, marchNap as marchNap2
where marchNap1.direct = framerec.direct
30 and marchNap2.direct = marchNap1.direct
and marchNap1.division = framerec.division
and marchNap1.division = marchNap2.division
and marchNap2.recno = marchNap1.recno+1")
| framerec in FrameRecs}
35
% Label the cities along the march
let labeloffset = .2 in
{make d2:label with
d2.location = frameTemp.map(recc.lonc - labeloffset, recc.latc + labeloffset),
40 d2.label = recc.city,
d2.color = ColorMap("blue")
| recc in SQL("select lonc, latc, city from marchCity")}
Figure 4: Partial specification of the Minard graphic depicted in Figure 3. This specification does not include the temperature
plot.
A LANGUAGE FOR SPECIFYING INFORMATIONAL GRAPHICS FROM FIRST PRINCIPLES
9

values and include the primitive types of point, cir-
cle, line, oval, rectangle, polygon, polar segment, and
labels. Scales are used for mapping data values to
their visual representations and are graphically repre-
sented by axes and legends. A scale is associated with
a coordinate system object and defines a transforma-
tion from the default layout canvas to a frame of type
twodcart or twodpolar (at this time).
In addition to a unique identifier, each object type
has predefined attributes, with conditions expressed
as constraints on these attributes. Constraints can
be of type equality (‘=’) or approximate equality
(‘˜’). Constraints enforcing visual organization fea-
tures (Kosak et al., 1994) such as non-overlap, align-
ment, or symmetry, can be applied to a set of graphi-
cal objects. These types of constraints are particularly
useful in specifying network diagrams (Ryall et al.,
1997). While such constraints can be specified in the
language, our current implementation only supports
constraints in the form of equalities.
All of the generic objects have a color attribute
and at least one location attribute, represented by a
coordinate. For 2-D objects, a Boolean fill attribute
defaults to true, indicating that the interior of that
object be filled in with the specified color. This at-
tribute also applies to line objects, which have start
and end widths. When widths are specified, lines are
rendered as four-sided polygons with rounded ends.
Each type of scale object has its own set of at-
tributes. A coordinate system object’s parent at-
tribute can reference another coordinate system object
or the canvas itself. The mapping from data values to
graphical values can be specified by conditions on its
origin and unit attributes. Alternatively, a condi-
tion can be applied to its map attribute in the form of
a user-defined mapping function that denotes both the
parent object and the scale. Thus, a twodcart object
whose parent is Canvas, origin is (5, 10), and unit
is (30, 40) can be defined by the mapping function:
Canvas.map(30x + 5, 40y + 10).
Axes are defined in terms of their origin, ll
(lower left) and ur (upper right) coordinates, and
tick marks. Legends can be used to graphically as-
sociate a color gradient with a range of data values by
assigning a color scale object to the scale attribute
and a coordinate to the location attribute. Discrete
colors can also be associated with data values, as in
the Minard Graph example, where tan represents “Ad-
vance” and black represents “Retreat.”
Attributes can also be defined by the user within
a make statement. For example, it is often helpful to
declare temporary variables for storing data retrieved
from a database. These user-defined attributes are ig-
nored when the specified visualization is rendered.
Another construct for an objspec is the type state-
ment. This is used for defining a new object type
that satisfies a set of conditions. These conditions
are either constraints on attribute properties or other
objspecs. An example of the former would be a con-
dition requiring that the color attribute for a new chart
type be “blue.” An example of the latter is to require
that a chart include a 2-D Cartesian coordinate frame
for use in rendering its display and that this frame con-
tain a set of lines and points corresponding to data re-
trieved from a database.
A third type of objspec is a set of objects, a set-
spec. This takes the form of either a query string or
a set of objspecs to be instantiated for each record re-
trieved by a query string. These two constructs are
often used in conjunction with one another to asso-
ciate data with generic graph objects. For example,
a setspec may define a query that retrieves two val-
ues, x and y, from a database table. A second setspec
can then specify a make command for rendering a set
of points located at the x and y values retrieved by
the query. Alternatively, the query can be contained
within the make statement itself, as shown in the code
for the scatter plots in Section 2.
It is often useful to associate a variable name
with an objspec so that it can be referenced
later. This is accomplished with the let state-
ment, which provides access to that variable within
the body of the statement. Because this construct
is commonly used in conjunction with a make or
type statement, two shorthand expressions have
been provided. The first of these is an abbre-
viated form of the let statement in which the
make clause is not explicitly stated, with: let
var:type with conditions in body corre-
sponding to let var = make var:type with
conditions in body. Similarly, the define
statement associates a new object definition with
a variable name, where: define var:type with
conditions in body expands to let var =
type var:type with conditions in body.
Figure 5 demonstrates the usage of the above ob-
jspec constructs for defining a new type of object
called a netplot. The code specifies the creation
of a set of circles, referred to as nodes, with radius
of 5, color of “black,” and center locations corre-
sponding to x and y values queried from a database
and mapped to a frame. (Data values were estimated
from a depiction of the ARPAnet circa 1971 avail-
able at http://www.cybergeography.org/atlas/
historical.html.) A set of red lines are also speci-
fied, with the endpoint locations of the lines equal to
the centers of the circles.
The output generated from this specification is
ICSOFT 2007 - International Conference on Software and Data Technologies
10

define n:netplot with
let frame:twodcart with frame.map = n.map
in
let nodes =
{make c:circle with
c.center = frame.map(rec.x, rec.y),
c.radius = n.radius,
c.color = n.ccolor
| rec in n.netRecs}
in
{make l:line with
l.start = nodes[rec.v1].center,
l.end = nodes[rec.v2].center,
l.color = n.lcolor
| rec in n.edgeRecs},
{make d:label with
d.location = frame.map(rec.x + 2,
rec.y - 1),
d.label = rec.node,
d.color = n.ccolor
| rec in n.netRecs}
in
make net:netplot with
net.map(x,y) = Canvas(7*x, 7*y),
net.netRecs = SQL("select node, x, y
from ArpaNodes"),
net.radius = 5,
net.edgeRecs = SQL("select v1, v2
from ArpaLinks"),
net.lcolor = ColorMap("red"),
net.ccolor = ColorMap("black");
Figure 5: Specification of the ARPAnet graphic depicted in
Figure 6.
shown in Figure 6. This chart and the Minard graphic
from the prior section demonstrate the flexibility and
control for specifying visualizations that result from
working with the right set of first principles. Further,
the intricacies of the code required to generate these
charts are hidden behind a relatively simple to use but
powerful grammar.
5 IMPLEMENTATION
The output generation process that renders visualiza-
tions from code written in our language, such as those
shown in the prior sections, involves four stages.
1. The code is parsed into an abstract syntax tree rep-
resentation.
2. The tree is traversed to set variable bindings and to
evaluate objspecs to the objects and sets of objects
that they specify. These objects are collected, and
the constraints that are imposed on them are accu-
mulated as well.
3. The constraints are solved. In the current imple-
mentation, the restriction to strict equality con-
straints means that solution is trivial, essentially
by congruence closure. We plan to solve the more
expressive constraints as in related work on the
GLIDE system (Ryall et al., 1997), by reduction to
mass-spring systems and iterative relaxation, to-
gether with user advice to eliminate local minima.
4. The objects are rendered. Any primitive graphic
object contained in the collection is drawn to the
canvas using graphical values determined as a re-
sult of constraint satisfaction.
6 RELATED WORK
Standard charting software packages, such as Mi-
crosoft Chart or DeltaGraph, enable the generation of
predefined graphic layouts selected from a “gallery”
of options. As argued above, by providing pre-
specified graph types, they provide simplicity at the
cost of the expressivity that motivates our work.
More flexibility can be achieved by embedding
such gallery-based systems inside of programming
languages to enable program-specified data manipu-
lations and complex graphical composites. Many sys-
tems have this capability: Mathematica, Matlab, Igor,
and so forth. Another method for expanding expres-
siveness is to embed the graph generation inside of
a full object-drawing package. Then, arbitrary addi-
tions and modifications can be made to the generated
graphics by manual direct manipulation. Neither of
these methods extend expressivity by deconstructing
the graphics into their abstract information-bearing
parts, that is, by allowing specification from first prin-
ciples.
Towards this latter goal, discovery of the first prin-
ciples of informational graphics was pioneered by
Bertin, whose work on the semiology of graphics
(Bertin, 1983) provides a deep analysis of the prin-
ciples. It is not, however, formalized in such a way
that computer implementation is possible.
Computer systems for automated generation of
graphics necessarily require those graphics to be built
from a set of components whose function can be for-
mally reasoned about. The seminal work in this area
was by Mackinlay (Mackinlay, 1986), whose system
could generate a variety of standard informational
graphics. The range of generable graphics was ex-
tended by Roth and Mattis (Roth and Mattis, 1990)
in his SAGE system. These systems were designed
for automated generation of appropriate informational
graphics from raw data, rather than for user-specified
visualization of the data. The emphasis is thus on the
functional appropriateness of the generated graphic
rather than the expressiveness of the range of genera-
ble graphics.
A LANGUAGE FOR SPECIFYING INFORMATIONAL GRAPHICS FROM FIRST PRINCIPLES
11

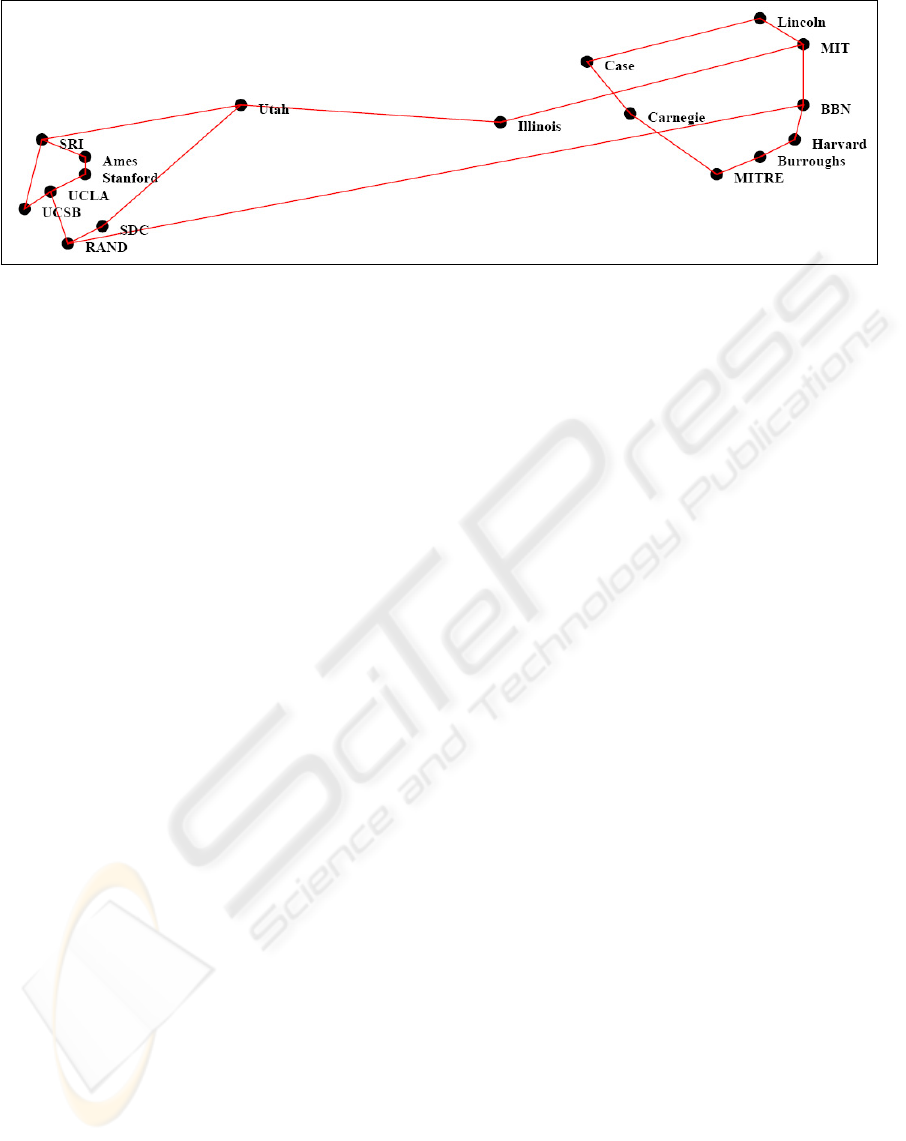
Figure 6: A network diagram depicting the ARPAnet circa 1971.
The SAGE system serves as the basis for a user-
manipulable set of tools for generating informational
graphics, SageTools (Roth et al., 1995). This sys-
tem shares with the present one the tying of graphi-
cal properties of objects to data values. Unlike Sage-
Tools, the present system relies solely on this idea,
which is made possible by the embedding of this
primitive principle in a specification language and the
broadening of the set of object types to which the prin-
ciple can be applied.
The effort most similar to the one described here
is Wilkinson’s work on a specification language for
informational graphics from first principles, a “gram-
mar” of graphics (Wilkinson, 1999). Wilkinson’s sys-
tem differs from the one proposed here in three ways.
First, the level of the language primitives are consid-
erably higher; notions such as Voronoi tesselation or
vane glyphs serve as primitives in the system. Second,
the goal of his language is to explicate the semantics
of graphics, not to serve as a command language for
generating the graphics. Thus, many of the details of
rendering can be glossed over in the system. Lastly,
and most importantly, the ability to embed constraints
beyond those of equality will provide us the capac-
ity to generate a range of informational graphics that
use positional information in a much looser and more
nuanced way. This latter advantage will distinguish
the present work from all previous work in the area
with the exception of the GLIDE system for network
diagram drawing. We hold for future work the imple-
mentation of a GLIDE-like facility for satisfying the
generated constraints.
7 CONCLUSIONS
We have presented a specification language for de-
scribing informational graphics from first principles,
founded on the simple idea of instantiating the graph-
ical properties of generic graphical objects from con-
straints over the scaled interpretation of data values.
This idea serves as a foundation for a wide variety of
graphics, well beyond the typical sorts found in sys-
tems based on fixed galleries of charts or graphs. By
making graphical first principles available to users,
our approach provides flexibility and expressiveness
for specifying innovative visualizations.
REFERENCES
Bertin, J. (1983). Semiology of Graphics. University of
Wisconsin Press.
Kosak, C., Marks, J., and Shieber, S. (1994). Automating
the layout of network diagrams with specified visual
organization. Transactions on Systems, Man and Cy-
bernetics, 24(3):440–454.
Mackinlay, J. (1986). Automating the design of graphical
presentations of relational information. ACM Trans-
actions on Graphics, 5(2):110–141.
Roth, S. F., Kolojejchick, J., Mattis, J., and Chuah, M. C.
(1995). Sagetools: An intelligent environment for
sketching, browsing, and customizing data-graphics.
In CHI ’95: Conference companion on Human fac-
tors in computing systems, pages 409–410, New York,
NY, USA. ACM Press.
Roth, S. F. and Mattis, J. (1990). Data characterization for
graphic presentation. In Proceedings of the Computer-
Human Interaction Conference (CHI ’90).
Ryall, K., Marks, J., and Shieber, S. M. (1997). An inter-
active constraint-based system for drawing graphs. In
Proceedings of the 10th Annual Symposium on User
Interface Software and Technology (UIST).
Wilkinson, L. (1999). The Grammar of Graphics. Springer-
Verlag, New York, NY.
ICSOFT 2007 - International Conference on Software and Data Technologies
12