DEVELOPMENT OF A SELF-CHECK SYSTEM FOR MENTAL

HEALTH USING A PULSE WAVE MOUSE

Mayumi Oyama-Higa

, Teijyu Miao

, Kazuo Sato

, Kazuyoshi Tanaka

and Huaichang Cheng

Department of Integrated Psychological Science, Kwansei Gakuin University, 1-1-155, Ichibancho

Uegahara Nishinomiya-City, 662-8501, Japan

Chaos Technical Research Laboratory and CCI Incorporation, 3-1-2401 Ryodocho

Nishinomiya-City, 662-0841, Japan

Research & Development Center, Hitachi Systems & Services, Ltd. 10-70, 2-Chome

Nanbanaka, Naniwa-ku, Osaka, 556-0011, Japan

Bio-feedback and Measurement Group, College of Physics, Jilin University, Changchun, China

Keywords: Pulse wave, Chaos analysis, Lyapunov exponent, Divergence, Mental health, Pulse wave mouse.

Abstract: We applied nonlinear chaos analysis to fingertip pulse wave data and found that the Lyapunov exponent, a

measure of the “divergence” of the trajectory of the attractor, was a useful index of mental health in

humans, particularly for the early detection of dementia and depressive psychosis, and for monitoring

mental changes in healthy persons. We developed an easy-to-use economical device, a PC mouse with an

integrated sensor for measuring the pulse waves, and its required software, to make the measurements.

After about 1 min of measurement, the Lyapunov exponent is calculated and displayed as a graph on the

PC. An advantage of this system is that the measurements can be made very easily and mental health can be

assessed when the PC is not being used for other work. Moreover, the measured data can be saved

according to the time and date, so diurnal changes and changes over longer time periods can be monitored

as a time series. The changes in the Lyapunov exponent are displayed on the PC as constellation graphs.

1 INTRODUCTION

In Japan, the annual number of suicides has reached

30,000 in each of the past 3 years, with many being

caused by serious depressive psychosis. Japan has

world’s highest life expectancy, and dementia has

increased along with the aging population. This has

become a social problem, and appropriate handling

by the family of the patient and society is essential

for both depressive psychosis and dementia. Quite

often, however, these ailments advance without the

patient being aware of the condition, and thus early

detection and treatment are necessary.

Routine daily checking of the person’s behaviour

and condition is necessary for detecting depressive

psychosis and dementia. Subjective observations

alone are not sufficient, and objective data must be

gathered using scientific methods. Previously used

methods include electroencephalography and

diagnostic brain imaging, both of which require a

high level of technical ability and knowledge. These

are not convenient measurement methods when the

time and cost are considered, and thus simple and

economical methods are needed. We earlier

demonstrated that the “divergence” of the attractor

trajectory obtained by nonlinear analysis of fingertip

pulse waves was a useful index for assessing mental

health. It was particularly effective in the detection

of dementia and the diagnosis of depressive

psychosis (Oyama-Higa et al., 2006). With this

technique, the pulse wave data, which have chaotic

behaviour, are measured for a few minutes. The data

are subjected to nonlinear analysis and the largest

Lyapunov exponent, which is a measure of the

divergence of the attractor trajectory, is calculated.

In addition, patients are asked to answer some

simple questions and record simple statements about

their condition at the time of taking the

239

Oyama-Higa M., Miao T., Sato K., Tanaka K. and Cheng H. (2007).

DEVELOPMENT OF A SELF-CHECK SYSTEM FOR MENTAL HEALTH USING A PULSE WAVE MOUSE.

In Proceedings of the Second International Conference on Software and Data Technologies, pages 239-248

DOI: 10.5220/0001322702390248

 SciTePress

measurements to encourage self-reporting of their

physical health status. The personal ID code, date

and time of measurement, fingertip pulse wave data,

and the patient responses and a brief statement about

their condition at the time of measurement are stored

as time series data to create a database. The user

searches the database for data pertaining to multiple

measurement time points and displays the change in

divergence with time or date on a constellation

graph that we have devised. The changes in mental

health and the self-reported status at the time of

measurement are fed back to the subject, whose

pulse waves were measured, making self-assessment

possible. In Section 2, we explain the method of

calculating the “divergence value” by applying the

nonlinear analysis of fingertip pulse wave data and

the self-check details. In Section 3, we discuss the

relevance of using fingertip pulse wave data and the

relationship between the “divergence value” and the

psychology of dementia. The mental health self-

check system is outlined in Section 4 and the

effectiveness and shortcomings of the system, along

with future plans, are discussed in Section 5.

2 CALCULATION OF THE

“DIVERGENCE” VALUE

OF FINGERTIP PULSE WAVES

AND DETAILS OF

SELF-CHECKING

2.1 Method of Measuring Fingertip

Pulse Waves

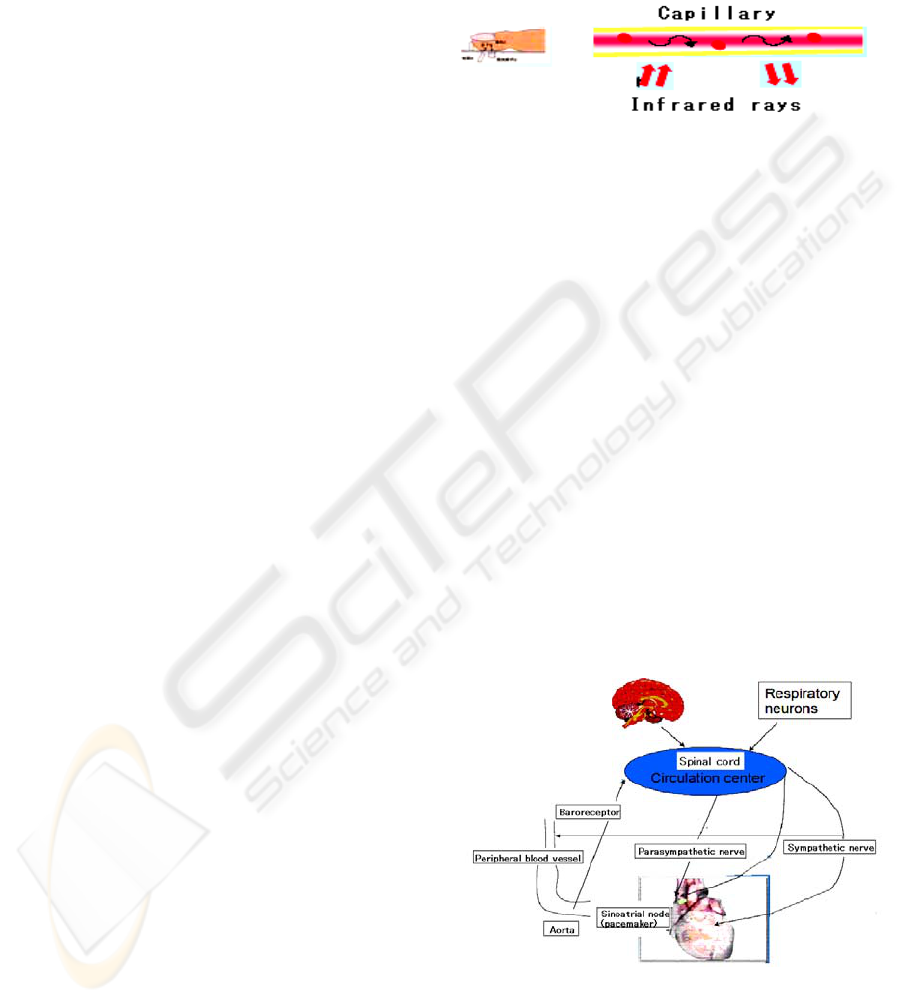
Fingertip pulse waves, which are linked to the

bioinformation network, were measured to

determine the divergence. Fingertip pulse waves

have been found to have chaotic characteristics

(Tsuda et al., 1992), (Sumida et al., 2000), (Miao,

2006). Changes in the amount of haemoglobin

flowing through the capillaries can be measured by

irradiating them with an infrared beam, as shown in

Figure 1. The waveform is naturally synchronised

with the beating of the heart, but the information is

different from the cardiac wave. The changes in

haemoglobin level caused by the constriction of

capillaries in the fingertip constitute time series data

of a complex system that include information from

the sympathetic and parasympathetic nerves. Pulse

wave data are collected at a frequency of 200 Hz

and a resolution of 12 bits. The measurement

duration is variable, depending on the experimental

conditions. Time series data consisting of 12,000

points could be obtained in 1 min of measurement.

Figure 1: Measurement of pulse waves through infrared

irradiation of capillaries. Frequency 200 Hz, resolution 12

bits.

The change in haemoglobin level in the capillaries is

believed to be related to the baroreceptors, which

are linked to the sympathetic and parasympathetic

nerves via the brain stem and the spinal cord, as

shown in Figure 2. This is a convenient method

because it does not require special care with regard

to the room temperature, place of measurement, and

measurement conditions. Moreover, because the

measurement time is very short, the data collection

is not a burden to the subject.

2.2 Chaos Analysis of the Pulse Wave

and Calculation of Divergence

(Lyapunov Exponent)

of the Attractor Trajectory

Figure 3 is a flow diagram showing the procedure,

from the measurement of pulse waves to calculation

of the Lyapunov exponent.

Figure 2: A conceptual diagram showing the flow of

information from the brain stem to peripheral blood

vessels through the action of sympathetic and

parasympathetic nerves.

ICSOFT 2007 - International Conference on Software and Data Technologies

240

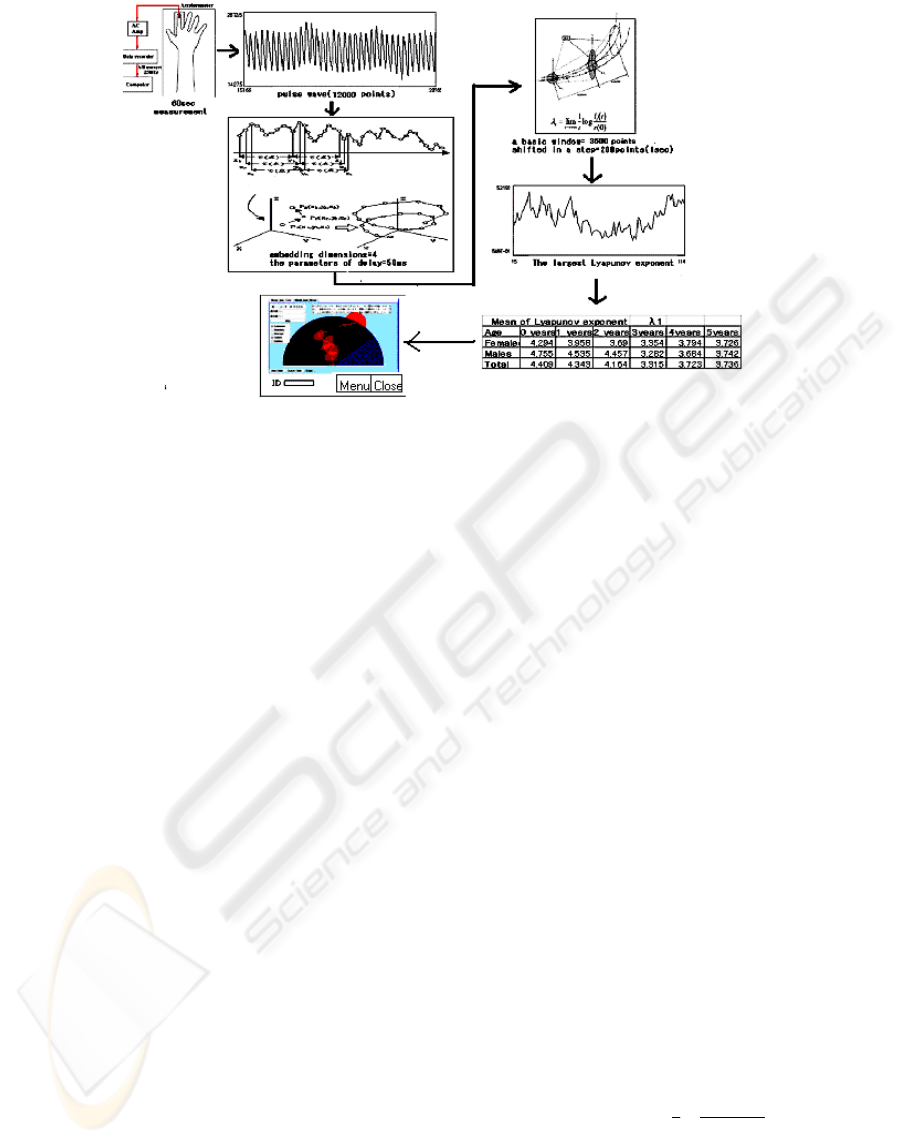
Figure 3: Flow diagram showing the procedure from the measurement of pulse waves to calculation of the Lyapunov

exponent.

To construct the attractor, we set a delay time

and the number of embedding dimensions according

to Tarkens (Takens, 1985), (Takens, 1981). We used

four embedding dimensions and a delay time of 50

msec (Sano and Sawada, 1985). Figure 3 illustrates

the method of embedding in three-dimensional

phase space. Although effective information can be

obtained from the shape of the four-dimensional

attractor, we calculated the Lyapunov exponent,

which is an index of trajectory instability and a

characteristic of chaos.

Our method of calculating the Lyapunov

exponent is explained in Figure 4, using three-

dimensional phase space as an example. We

assumed that a small sphere (hypersphere) of radius

ε is the initial value for a three-dimensional chaotic

dynamic system. After being mapped once, the

sphere was stretched in the e1 direction and

compressed in the e3 direction, and assumed the

shape of an ellipsoid, as shown in Figure 4. We

designated the logarithm of the expansion rate per

unit time along the directions e1, e2, and e3 as λ1,

λ2, and λ3, respectively. Here, λ1, λ2, and λ3 are the

Lyapunov exponents and their set is the Lyapunov

spectrum. We repeated the procedure of

representing this hypersphere as many times as the

calculation was iterated. After that, their sum was

taken and the average was determined to calculate

the Lyapunov spectrum. Because four embedded

dimensions were set as the optimum number of

dimensions for the pulse wave, we obtained the four

Lyapunov exponents, λ1, λ2, λ3, and λ4, as the

Lyapunov spectrum. Amongst these, the largest

Lyapunov exponent, λ1, was used in the calculation

to prepare the constellation graphs.

The calculation equations for the Lyapunov

exponent are shown below. For the time series data

x(i), with I = 1,…, and N obtained from the fingertip

pulse waves, the phase space was reconstructed

using the method of time delays. Assuming that we

create a d-dimensional phase space using a constant

time delay τ, the vectors in the space are generated

as d-tuples from the time series and are given by

)}({)))1((),...,(()( ixdixixi

=−

−

(1)

where

))1(()(

−−= kixix

, with k = 1,...,d. To

reconstruct the phase space correctly, the parameters

of delay (τ) and embedding dimensions (d) should

be chosen optimally (Sano and Sawada, 1985). In

time series data recorded from human finger

photoplethysmograms, we chose the parameters τ =

50 msec and d = 4, as in references (Tsuda et al.,

1992) and (Sumida et al., 2000).

In the reconstructed phase space, one of the

important measures of complexity is the largest

Lyapunov exponent

. If

)(tX

is the evolution of

some initial orbit

)0(X

in the phase space, with

time, then

|)(|

limlim

→∞→

(2)

where

)()()( ttt

εε

XXX

−

and

)0()0(

XX −=

DEVELOPMENT OF A SELF-CHECK SYSTEM FOR MENTAL HEALTH USING A PULSE WAVE MOUSE

241

for almost all initial difference vectors

)0()0(

XX −=

. We estimate

using the

algorithm of Sano and Sawada (Sano and Sawada,

1985), where

describes the divergence and

instability of the orbits in phase space.

Figure 4: Method of calculating the Lyapunov exponent.

The initial 8,000 points of pulse wave data were

taken as one window to calculate the largest

Lyapunov exponent, λ1. In the next step, the

window was shifted by 200 points and the exponent

was calculated from the next window of 8,000

points. This procedure was repeated until the pulse

wave data were exhausted. Three minutes of

measurement yielded 36,000 data points. Therefore,

we can obtain a (36,000 – 8,000)/200 = 140-point

time series of Lyapunov exponents, and with 1 min

of measurement, we can achieve a (12,000 –

8,000)/200 = 20-point time series of Lyapunov

exponents. The size of the hypersphere used was

0.08. The variation of the largest Lyapunov

exponent is a measure of the variation of the

trajectory of the four-dimensional attractor. The

largest Lyapunov exponent is the divergence of the

attractor trajectory and is an important value related

to psychological indices (Oyama-Higa and Miao,

2005), (Oyama-Higa and Miao, 2006).

2.3 Outline of Self-Checking at the

Time of Measurement

The subjects were asked to answer some simple

questions to ensure normal measurement of pulse

waves. This information was used to interpret the

observed divergence in measured values. The

questions were status-checking items, including

physical condition and a simple assessment of the

mood at the time of measurement. The answer was

chosen from one of three available choices. Apart

from these questions, the subjects were asked to

describe their mood and condition at the time of the

measurement in more definite terms. This enabled

the person to identify factors that affect the

divergence values. Because these records were made

in a free-form style, key words alone could be used.

However, when a subject is allowed to write freely,

for example, about things that he or she had

communicated to a friend, music he or she enjoyed,

positive results in a sporting activity, and good or

bad news that had been received, it is easier to study

the relationship of those events with the divergence

value.

The situations that elicit emotions such as

delight, anger, sorrow, and pleasure, differ from

person to person. For example, a condition that

creates a suitable level of divergence, such as

listening to music or having a conversation with

someone, need to be recorded as data unique to that

subject. In addition, extreme tension, fatigue, and

low spirits also cause changes in divergence.

Therefore, comparing the status recorded at the time

of measurement with the corresponding divergence

values helps a person to assess his or her own

mental status. Table 1 shows the details of the

questions with three levels of answers, and the

freestyle description method. These responses and

the simple comments on the subject’s condition are

stored so that they can be seen by clicking the

corresponding divergence value on the graph.

Table 1: An example of entering the subject’s state at the

time of measurement: Status checking items.

Freestyle reporting: The subject is also to enter a

note on his or her condition at the time of

measurement. These notes can be in the form of a

descriptive comment on the subject’s condition,

keywords, and more.

Comment example 1:

[Had a pleasant chat with a friend about hobbies.]

Comment example 2:

[Feeling low after failing a test]

We plan to vary the simple questions described

above according to the category (child, adult, or

aged person) of the subject.

ICSOFT 2007 - International Conference on Software and Data Technologies

242

3 RELATIONSHIP BETWEEN

THE DIVERGENCE VALUE

AND COGNITIVE

PSYCHOLOGY AND THE

RELEVANCE OF USING

FINGERTIP PULSE WAVES

Biological systems are considered to be complex,

fluctuating with chaotic characteristics. Although

chaotic systems appear to be extremely complicated

and to behave in a random and unstable manner,

they in fact change according to deterministic rules.

Biological signals emanating from humans, or vital

signs, come in many types, such as the body

temperature, blood pressure, and pulse rate.

Fingertip pulse waves are biological signals that

produce time series data with chaotic characteristics.

Moreover, unlike cardiac waves, fingertip pulse

waves contain various types of information, such as

that from the nervous system. In the field of

psychology, several methods have been suggested as

indices for assessing mental health. However, these

methods are generally subjective, and therefore lack

objectivity. Questionnaires have often been used as

relatively simple psychological tests, and the

measurement and analysis of brain waves can

objectively assess the neurological state at the time

of measurement. However, the measurements are

not simple, and the analysis methods are not yet

capable of analysing detailed psychological changes.

Another possible method for measuring biological

information is to analyse the R-R intervals of

heartbeats and pulse waves. However, no analysis

has attempted to take into account the chaotic

characteristics of biological information.

The Lyapunov exponent is a property of chaotic

systems that expresses the attractor and represents

the “divergence” of the attractor trajectory. We

focussed on the Lyapunov exponent, which had not

been quantitatively evaluated as an index of

psychological changes in humans, and investigated

its relationship with dementia and communication

skill (an ADL index) in aged persons (Oyama-Higa

et al., 2006), its relationship with error rate at work

(Imanishi and Oyama-Higa, 2006), its relationship

with diurnal changes and indices of cumulative

fatigue in employees (Miao, 2006), (Oyama-Higa

and Miao, 2005), (Oyama-Higa and Miao, 2006),

and the time series fluctuations in divergence in 0-

to 5-year-old children and the effect of parental

affection towards the children (Oyama-Higa et al,

2006).

It became clear that suitable functioning and

harmony of the sympathetic nerves, which are

related to the adaptability to the external

environment and the society, and flexibility,

spontaneity, and cooperativeness of the mind, are

important for humans to live in a mentally healthy

state. These values were related to the largest

Lyapunov exponent obtained by nonlinear analysis

(Oyama-Higa and Miao, 2005), (Oyama-Higa and

Miao, 2006). The largest Lyapunov exponent that

represents the time series variation in the attractor

trajectory is defined as “divergence.” When this

value remains continuously low (i.e., when a long

spell with low divergence persists), the person

would have a low ability to adapt to the external

world in their daily life and would be incapable of

maintaining a mentally healthy state. However, an

extremely tense or stressful state persists when the

divergence remains continuously high. A mentally

healthy state also cannot be maintained in this

situation. Normally in humans, a healthy state is the

condition in which constant variation occurs in the

divergence. Emotions are a part of being human, and

these are believed to cause the variation in

divergence.

Physical immunity is crucial for the maintenance

of human health, and lowered immunity causes

various diseases. Therefore, to prevent the lowering

of physical immunity and to increase resistance and

prevent diseases, we pay attention to what we eat,

rest, take medicines, and train to improve our

stamina. However, mental toughness, as reflected in

the ability to communicate in a positive manner,

willingness to do the given jobs, and the ability of

mental toughness to withstand drastic changes in the

external world, are also very important. We can call

these “mental immunity,” but no methods have been

developed to scientifically investigate such

immunity. We analysed fingertip pulse waves

through nonlinear analysis and examined their

relationship with various psychological indices, and

found that the largest Lyapunov exponent obtained

through chaos analysis, which corresponds to the

“divergence” of the attractor, was closely related to

mental immunity. It was also demonstrated that this

value was closely linked with functioning of the

sympathetic nerves of the autonomic nervous

system.

For humans, a mentally healthy condition means

having the ability to cope flexibly with external

changes in “divergence.” This can be considered

mental flexibility, or mental immunity, in contrast to

physical immunity. Mental immunity represents

DEVELOPMENT OF A SELF-CHECK SYSTEM FOR MENTAL HEALTH USING A PULSE WAVE MOUSE

243

adaptability to the external changes in that a person

has to face in his or her everyday life, including

one’s communication ability, ability of self-

expression, and suitability of psychological

flexibility. Whilst expressing themselves, humans

skillfully fend off various kinds of changes,

contacts, and assaults from the external

environment, and deal with or cope with them in

some cases. This is the essence of mental immunity.

Change occurs constantly in day-to-day life.

“Divergence,” which represents a change in the state

of mental immunity, is a critical index. At the same

time, divergence varies depending on various

conditions of the person. For example, a long time

period without “divergence” suggests that the person

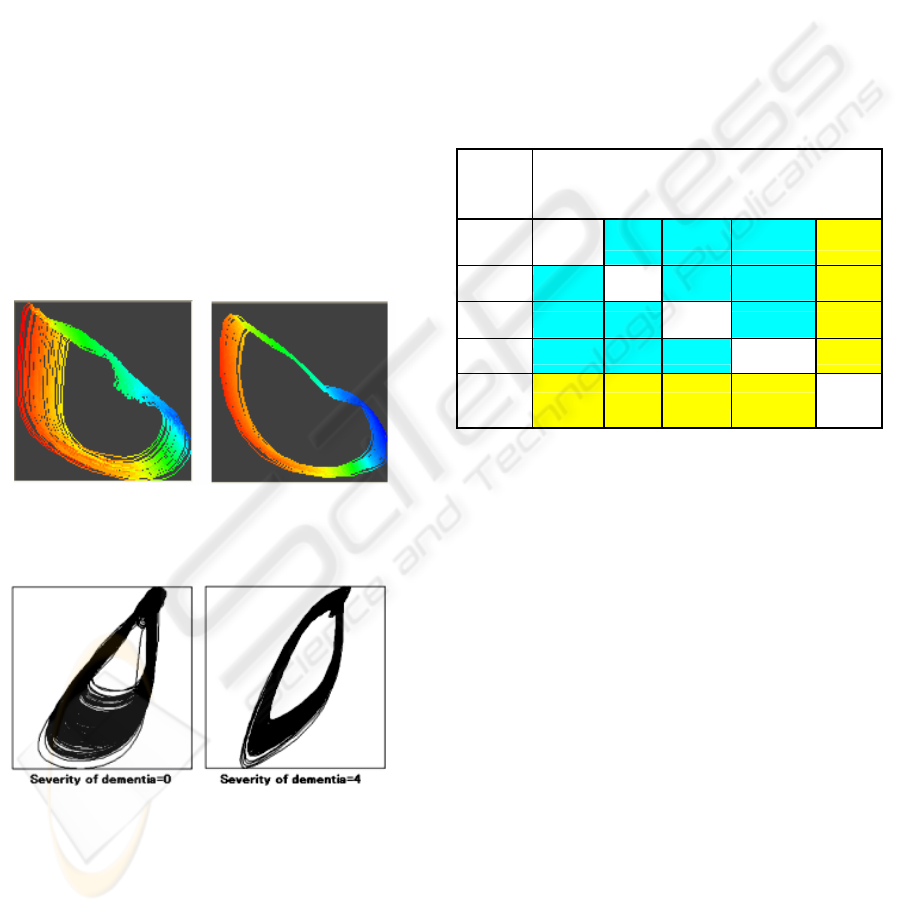
is not in a normal state. Figure 5 shows the attractors

of a mentally healthy person and a patient with

depressive psychosis. The depressed person has low

divergence. Figure 6 shows the attractors of two

dementia patients; both figures contain data from

elderly subjects. The divergence becomes smaller as

dementia advances. (CCI software was used.)

Healthy person Depressed patient

Figure 5: Attractors of a healthy person and a depressed

patient prepared from 30-sec measurements.

Figure 6: Attractors in old people with dementia of

severity 0 and 4.

In a normal state, the divergence level constantly

fluctuates. During times of extreme tension and

stress, continuously high divergence will exist.

Afterward, however, a mentally healthy person

naturally finds a way to relax, which brings the

divergence back to its normal state. However, a low

level of divergence would continue when a person is

in a depressed state or when age-related dementia is

present. This suggests that the person is incapable of

bringing back the divergence to its natural level on

his or her own, indicating a lowered adaptability to

the external environment.

Table 2 shows the comparison of the midday

Lyapunov exponent and the fatigue indices during

the work day of employees at a particular company.

The table indicates an inverse correlation of –0.7 or

greater between the midday Lyapunov exponent and

state of depression or anxiety of the employees.

Table 2: Coefficients of correlation between the Lyapunov

exponent (at midday) and components of mental fatigue in

company employees.

Willpower

decrement

Anxiety

State of

Depression

Accumulated

Tiredness

Lyapunov

exponent

midday

Willpower

decrement

0.7235 0.7539 0.7496 –0.6385

Anxiety 0.7235 1 0.8455 0.9358 –0.7279

State of

depression

0.7539 0.8455 1 0.842 –0.7014

Accumlate

d tiredness

0.7496 0.9358 0.842 1 –0.6305

Lyapunov

exponent

midday

–0.6385 –0.7279 –0.7014 –0.6305 1

The experiments conducted thus far have shown

that a suitable variation in the Lyapunov exponent is

related to an adaptability to the external

environment, which is necessary for a person to live

a healthy life. This value fluctuates constantly.

Therefore, by monitoring the fluctuations to detect

states with very little or too much variation, a person

could, on his or her own, assess one’s mental health.

Below, we outline this mental health self-check

system.

4 OUTLINE OF THE MENTAL

HEALTH SELF-CHECK

SYSTEM

4.1 Development of the Measuring

Equipment

A device that is easy to use and gives minimum

burden on the subject is needed to measure the pulse

waves. It is not possible to check the mental health

of a person through just one round of measurements.

For these reasons, the device must be convenient to

ICSOFT 2007 - International Conference on Software and Data Technologies

244

use. We took note of the fact many people often do

their work with PCs, and therefore developed a

device that can make these measurements using a

mouse. As shown in Figure 7, the pulse wave sensor

is installed on one side of the pulse wave (PW)

mouse; measurements can be made by simply

touching the sensor with a finger. The mouse is

connected to the PC through a USB port and can

also be used as an ordinary mouse (patent pending).

Figure 7: Mouse for measuring pulse waves.

Software installed on the PC starts and ends the

measurements, and sets their duration.

4.2 System Configuration

Figure 8 is a configuration diagram of the mental

health self-check system. A PW mouse icon is

created on the PC desktop, and the menu screen is

displayed by clicking on the icon.

The screens are structured so that clicking the

PW mouse icon on the screen displays the initial

screen of the program. The user can then navigate to

the measurement, search, or setup screens, where the

respective functions can be performed. In the

measurement section, the subject inputs his or her

ID, does the data collection, and answer questions.

In the pulse-wave-measuring step, the Lyapunov

exponent is computed, and after it is confirmed that

the pulse waves are being captured normally, the

data are saved. After the pulse wave measurements

are completed, the user answers the questions and

the answers are saved. When the pulse wave

measurements and the inputs of the answers to the

questions are completed, the system moves back to

the initial screen. If the person clicks the search

button, a list of saved data is displayed. The

constellation graph can be displayed by clicking the

desired date. From one to a maximum of ten dates

can be selected. The display is prepared according to

the sequence of the selected measurement dates. The

person can self-check his or her mental status by

examining the variation in the Lyapunov exponent

and the text displayed at the top right in the

constellation graph. The menu screen display is

structured so that various parameters can be changed

based on the initial screen setup. When default

values are used for the safe operation of the system,

the displays are based on the fixed settings.

Figure 8: Flow diagram of the mental health self-check system (fully PC based).

DEVELOPMENT OF A SELF-CHECK SYSTEM FOR MENTAL HEALTH USING A PULSE WAVE MOUSE

245

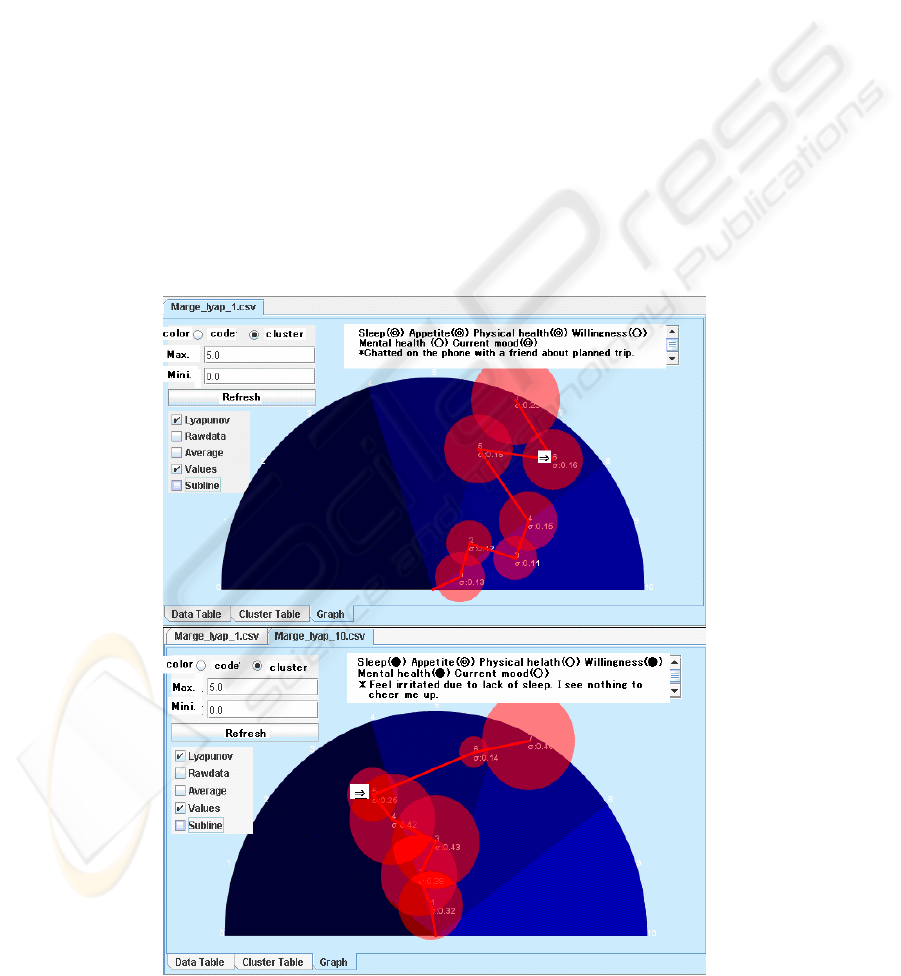
4.3 Display of Results and

Constellation Graphs

Figure 9 presents constellation graphs. The change

in divergence is displayed according to the selected

dates of measurement. When a large divergence

occurs, the line moves to the right, and when it is

small, the line shifts to the left.

The results of seven measurements are displayed

simultaneously. The circles around each point

represent the standard deviation. When the cursor is

placed over the centre of a circle, the display in the

box at the top right changes to show the information

that corresponds to that measurement.

As noted in Section 2.2, 1 min of pulse wave

measurements yields a 20-point time series of

Lyapunov exponents. The mean and standard

deviation are calculated. Each mean value of the

Lyapunov exponent is converted into an angle, with

180° assigned the maximum value of 5.0 and 0°

given the minimum value of 0.0, and displayed as a

vector on the constellation graph. For displaying the

data of n number of measurement dates, the radius r

of the full semicircle is divided into n equal sections,

and n equidistant concentric semicircles are drawn.

The sequence of the time series is set from the centre

towards the outside. The n Lyapunov exponents of

this time series are converted into angles and

represented as a series of connected vectors. The

point at which a vector intersects the corresponding

semicircle is taken as the origin for the next vector

to obtain the type of graphs shown in Figure 9.

5 FUTURE PLANS AND THE

EFFECTIVENESS AND

DRAWBACKS OF THE

SYSTEM

We have described a system in which the entire

procedure is performed on a PC. In the future, we

Figure 9: Examples of time series constellation graphs.

ICSOFT 2007 - International Conference on Software and Data Technologies

246

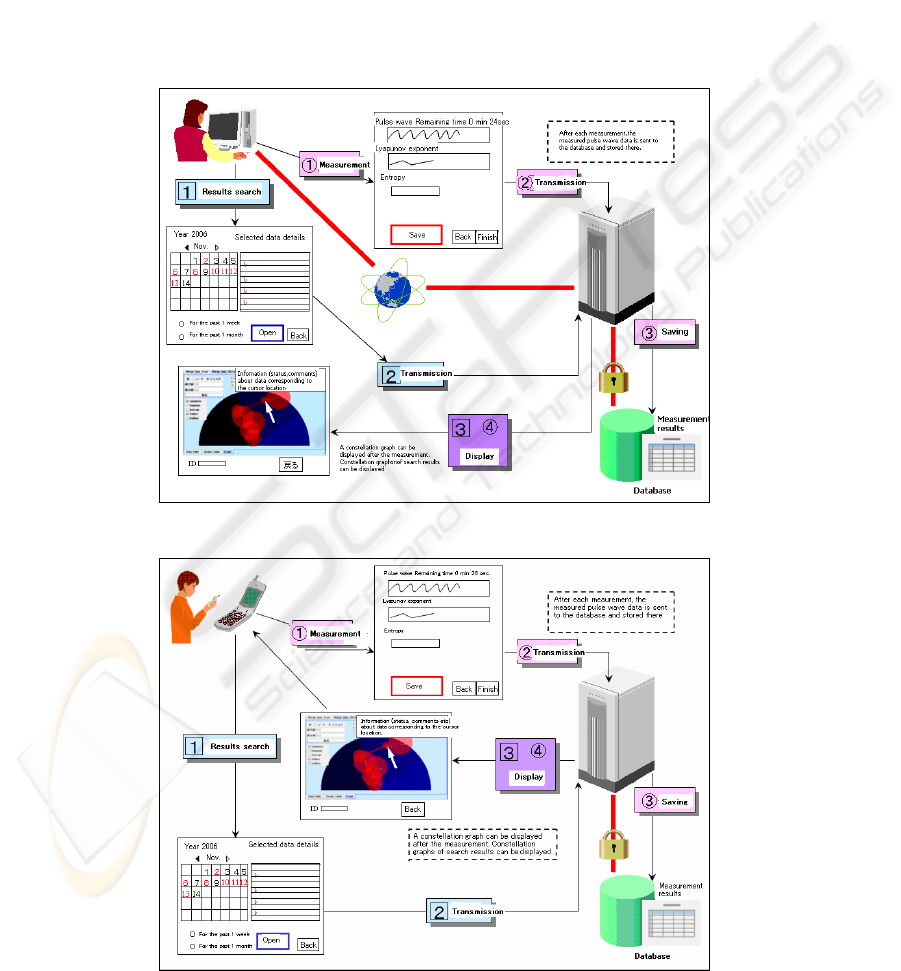
plan to develop this into an Internet-based system,

with software kept on a server and launched by

clicking an icon. Pulse-wave data, answers to the

questions, and the descriptive comments would be

stored under the person’s ID in a database created

on the server. Thus, data from a larger number of

users can be collected to facilitate a more effective

analysis.

To encourage more people to use the system, we

are also considering incorporating the PW mouse

into cell phones to allow the display to be viewed on

cell phone screens. When using cell phones, the data

processing would be achieved by downloading the

software and searching the database via the Internet

in the I-mode. The use of Internet-based methods

would produce a vast amount of data, and privacy-

protection issues would have to be thoroughly

addressed.

The following are conceptual diagrams of the

fully PC-based system, an Internet-based system,

and a cell phone-based system.

A. Fully PC-based system (See Figure 8).

B. Internet-based system.

C. Cell phone-based system.

Figure 10: The Internet-based system.

Figure 11: The cell phone-based system.

DEVELOPMENT OF A SELF-CHECK SYSTEM FOR MENTAL HEALTH USING A PULSE WAVE MOUSE

247

6 CONCLUSION

The system described above allows a person to self-

check his or her mental health level and also enables

self-management. Appreciating the mental states

that give rise to high or low divergence in day-to-

day life would help to maintain mental health. We

firmly believe that when a person can no longer

exercise self-control, the early detection of

depressive psychosis or dementia through

consultation with a counselor or psychiatrist, and the

prevention of deteriorating mental health, would be

possible. Moreover, if data related to the

psychological indices of persons could be sent and

received through a network, this could lead to

previously unknown communication innovations.

Nevertheless, we must to pay great attention to data

management because of recent problems in

protecting personal information. In terms of the

system’s effectiveness from a research point of

view, we are certain that accumulating vast amounts

of information would be useful in various future

studies on pulse waves.

REFERENCES

Oyama-Higa M., Miao T., and Mizuno-Matsumoto Y.,

(2006) Analysis of dementia in aged subjects through

chaos analysis of fingertip pulse waves, 2006 IEEE

Conference on Systems, Man, and Cybernetics 2006,

Taipei, Taiwan, 2863–2867.

Tsuda I., Tahara T., and Iwanaga I., (1992) Chaotic

pulsation in capillary vessels and its dependence on

mental and physical conditions. Int. J. Bifurcation and

Chaos 2: 313–324.

Sumida T., Arimitu Y., Tahara T., and Iwanaga H., (2000)

Mental conditions reflected by the chaos of pulsation

in capillary vessels. Int. J. Bifurcation and Chaos 10:

2245–2255.

Sano M. and Sawada Y., (1985) Measurement of the

Lyapunov spectrum from a chaotic time series. Phys.

Rev. Lett. 55: 1082.

Miao T., Shimoyama O., and Oyama-Higa M., (2006)

Modelling plethysmogram dynamics based on

baroreflex under higher cerebral influences, 2006

IEEE Conference on Systems, Man, and Cybernetics

2006, Taipei, Taiwan, 2868–2873.

Oyama-Higa M. and Miao T., Representation of a physio-

psychological index through constellation graphs,

ICNC’05–FSKD’05., http://dx.doi.org/10.1007/

11539087_109.

Oyama-Higa M. and Miao T., (2006) Discovery and

application of new index for cognitive psychology,

2006 IEEE Conference on Systems, Man, and

Cybernetics 2006, Taipei, Taiwan, 2040–2044.

Imanishi A. and Oyama-Higa M., (2006) The relation

between observers’ psychophysiological conditions

and human errors during monitoring task, 2006 IEEE

Conference on Systems, Man, and Cybernetics 2006,

Taipei, Taiwan, 2035–2039.

Oyama-Higa M., Tsujino J., and Tanabiki M., (2006)

Does a mother’s attachment to her child affect

biological information provided by the child? Chaos

analysis of fingertip pulse waves of children, 2006

IEEE Conference on Systems, Man, and Cybernetics

2006, Taipei, Taiwan, 2030–2034.

Takens F, in: Braaksma B L J, Broer H W, and Takens F,

eds (1985) Dynamical Systems and Bifurcations,

Lecture Notes in Math. Vol. 1125, Springer,

Heidelberg.

Takens F (1981) Detecting Strange Attractors in

Turbulence, Lecture Notes in Math. Vol. 898,

Springer, New York.

ICSOFT 2007 - International Conference on Software and Data Technologies

248