ANALYZING EBAY NEGOTIATION PATTERNS

A. Pereira, L. Rocha, F. Mour˜ao, T. Torres, W. Meira Jr.

Department of Computer Science, Federal University of Minas Gerais, Brazil

P. Goes

School of Business, University of Connecticut, USA

Keywords:

Online auctions, e-business, characterization methodology, reactivity.

Abstract:

Online auctions have several aspects that violate the common assumptions made by the traditional economic

auction theory. An online auction can be seen as an interactive economic information system, where user-

system interactions are usually very complex. It is important to note that the interactions are not isolated, but

successive interactions become a loop-feedback mechanism, that we call reactivity, where the user behavior

affects the auction negotiation and vice-versa. In this paper we describe a new hierarchical characterization

model for online auctions and apply this model to a real case study, showing its advantages in discovering

some online auction negotiation patterns. The results demonstrate that our characterization model provides

an efﬁcient way to open the auction dynamics’s “black box”. We also propose an abstraction named Auction

Model Graph (AMG) which enables the temporal analysis of the negotiation. This work is part of a research

to analyze reactivity in e-business, that may contribute to understand the business dynamics and has wide ap-

plicability to activities such as designing recommendation agents, service personalization, and site interaction

enhancement.

1 INTRODUCTION

Online auctions have several aspects that violate the

common assumptions made by the traditional eco-

nomic auction theory. The auction duration is typi-

cally much longer than in traditional auctions; bidders

may enter and exit at any time; bidders are geographi-

cally dispersed all over the world; they have very dis-

tinct backgrounds and it is hard to predict how many

bidders will end up participating in the auction.

An online auction may be seen as an interactive

economic information system, where user-system in-

teractions are usually very complex. It is important to

note that the interactions are not isolated, but succes-

sive interactions become a loop-feedbackmechanism,

which we call reactivity, where the user behavior af-

fects the auction negotiation and vice-versa.

An online auction is a rather complex e-business

application to characterize because of its many at-

tributes and dynamic aspects. It has an initial state

deﬁned by its input parameters, such as the beginning

date and the starting bid. Its intermediary state is the

phase when the negotiation occurs through bids. The

ﬁnal state occurs after the negotiation and is charac-

terized by its output parameters, such as the winning

price, the winner bidder, and the number of bids.

In this paper we describe a new hierarchical char-

acterization model for online auctions. Despite the

existence of other characterization models (Roth and

Ockenfels, 2002; Bapna et al., 2004; Easley and

Tenorio, 2004), none of them is capable of under-

standing the factors that explain the auction dynam-

ics (Achtert et al., 2005), which is the basis of our re-

search. Moreover, we apply this model to a real case

study, showing the advantages of our model in order

to discover the online auction negotiation patterns.

This work is part of a research to analyze reac-

tivity in e-business, which has wide applicability for

activities such as designing recommendation agents,

service personalization, and site interaction enhance-

ment (Chelcea et al., 2005).

The key aspect of reactivity is how users, or bid-

ders in the case of online auctions, react to system’s

or application’s behavior. The behavior may mean

Pereira A., Rocha L., Mourão F., Torres T., Meira Jr. W. and Goes P. (2007).

ANALYZING EBAY NEGOTIATION PATTERNS.

In Proceedings of the Third International Conference on Web Information Systems and Technologies - Society, e-Business and e-Government /

e-Learning, pages 84-91

DOI: 10.5220/0001267000840091

 SciTePress

Market

OutputInput

Dynamics

Auction

3 4 5

1) How the market affects the input?

2) How the market affects the dynamics?

3) How the input affects the auction dynamics?

4) How the auction dynamics affects itself?

5) How the auction dynamics affects the output?

Figure 1: Auction Dynamics - Reactivity.

the performance of the system in the case of a phys-

ical level analysis, or business rules and dynamics in

a logical level view. At the physical level, we have

modeled reactivity (Pereira et al., 2004) and quanti-

ﬁed its impact (Pereira et al., 2006b) on the perfor-

mance of Internet services. The logical view of the

service, e.g., how the business dynamics affect the

user behavior,is the current focus of our research. We

chose online auctions as the application to analyze,

sine it is a popular, rich and complex online service.

Figure 1 shows a high-level representation of the

auction. There are ﬁve different reactivity dimensions

to analyze, as illustrated by the numbered questions.

The paper is organized as follows. Section 2 pro-

vides an overview of related work in the realm of on-

line auctions. Section 3 presents the hierarchical char-

acterization model. Section 4 describes our case study

of eBay, showing the main results through the appli-

cation of our model. Finally, Section 5 presents the

conclusions and outlines ongoing work.

2 RELATED WORK

Online auctions have been studied extensively lately.

Many studies focus on validating concepts from the

classic economic theory of auctions in the online en-

vironment. For example, Lucking-Reiley (Lucking-

Reiley, 1999) checks the validity of the well-known

results of revenue equivalence. Bajari and Hor-

tacsu (Bajari and Hortacsu, 2003) address how

the starting bid set by the seller affects the win-

ner’s course. Gilkeson and Reynolds (Gilkeson and

Reynolds, 2003) show the importance of a proper

starting bid price to attract more bidders and make an

auction successful.

The growing popularity of auction sites on the

Internet and the increasing importance of online

auctions as exchange mechanisms have attracted

the attention of academic researchers who have

studied such issues as the effect of auction for-

mats (Lucking-Reiley, 1999), the last-minute bidding

phenomenon (Roth and Ockenfels, 2002) and the

value of seller reputation (Melnik and Alm, 2002).

However, these studies are still limited to how they

explain bidding behavior over the entire sequence of

bids, as opposed to simply summary outcomes (e.g.,

ﬁnal auction prices, and number of bids) in an auc-

tion (Ariely and Simonson, 2003; Chakravarti et al.,

2002).

For addressing the issue of reactivity in online

auctions, it is important to take into account the work

that has been done on analyzing bidders’ and sellers’

behavior in online environments (Easley and Teno-

rio, 2004). Roth and Ockenfels (Roth and Ockenfels,

2002) study the timing of bids, and the impact of dif-

ferent methods of specifying auction deadlines. By

comparing eBay and Amazon auctions, they ﬁnd ev-

idence that auctions held with a “soft” ending time

discourage late bidding (also known as “sniping”), a

common behavior observed on eBay. Using data from

ubid.com, Bapna et al. (Bapna et al., 2004) develop

a cluster analysis approach to classify online bidders

into four categories: participators, evaluators, oppor-

tunists, and sip-and-dippers. In another paper, Bapna

et al. (Bapna et al., 2003) develop a simulation model

emulating bidders’ behavior to analyze their impact

in the outcome of the auctions.

Although there are several detailed studies of on-

line auctions, none of them deals with reactivity. We

believe that this concept will allow a better character-

ization of online auctions and other distributed appli-

cations, qualifying and quantifying temporal and se-

quencing aspects.

3 CHARACTERIZATION

METHODOLOGY

This section presents our hierarchicalcharacterization

model, which applies the concept of reactivity to gain

a better understanding of the dynamics of online auc-

tions.

ANALYZING EBAY NEGOTIATION PATTERNS

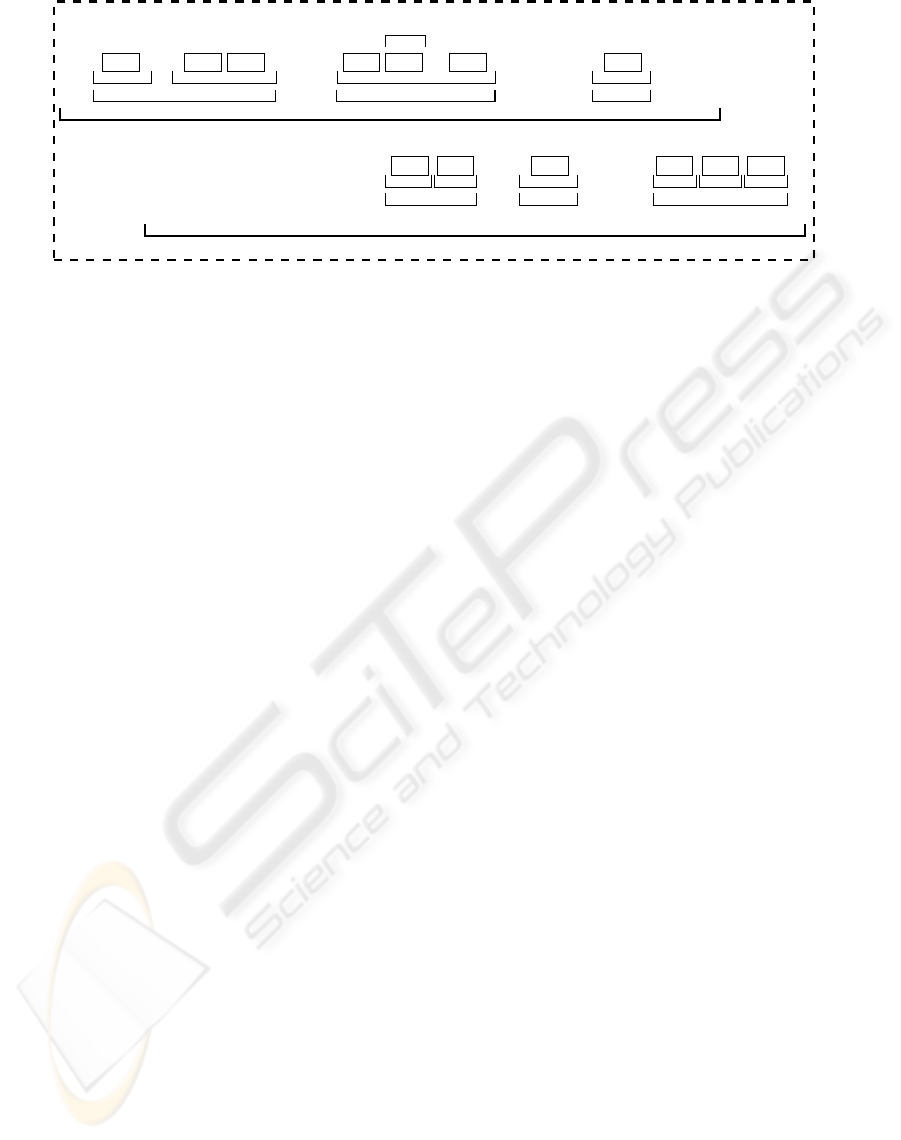
2 2 2 31 1

Ses 2 Ses 3

Ses 4

Ses 5

Seq 2 Seq 3

Auction 1

Ses 1

Seq 1

Auction2

1 14 5 4 6

Ses 1

Seq 1 Seq 2 Seq 3

Ses 2 Ses 3 Ses 4 Ses 5 Ses 6

Market

Figure 2: Auction Hierarchy.

Previous auction characterizations (Bapna et al.,

2004; Bapna et al., 2003; Roth and Ockenfels, 2002)

consider mainly the static aspects, as discussed in

Section 2. We propose a novel model that is able to

capture the relevant information about the auctionfea-

tures to understand its dynamics. These criteria ana-

lyze the auctions at various levels of granularity and

are organized in a hierarchy.

A reactivity model deﬁnes agents who react to

events through actions (Pereira et al., 2006a). In the

online auctions environment, agents are bidders, their

actions are their bids, and events are bids from other

bidders. Another important concept in the reactivity

model is the time to react. In online auctions, because

of its long duration, the intermittent nature of the bid-

ders’ visits to the sites, and their own behavior char-

acteristics, the time to react induces the occurrence

of both synchronous and asynchronous reactivity pe-

riods. Synchronous in our model means two actions

occurring during the same period of activity.

In our characterization model we have incorpo-

rated these ideas in the deﬁnition of the basic com-

ponents of the model. The important objectives are

to isolate, measure and understand periods of syn-

chronous and asynchronous reactivity, how reactivity

leads to competitiveness, and the instantaneous im-

pact on the auction winning price, and the winner.

These are basic components necessary to understand

the auction dynamics.

There are two key concepts for modeling reactiv-

ity: activity and synchronicity. One auction is active

if bid occurred within a time threshold θ

ses

. One auc-

tion is synchronous when it is active and more than

one bidder submitted a bid within θ

ses

As illustrated in Figure 2, our characterization

model is organized as a ﬁve-level hierarchy: bid, ses-

sion, sequence, auction, and market. The bid (repre-

sented by rectangles containing a number that identi-

ﬁes the bidder) is the ﬁnest grain level, representing

the bidder’s action. A session is a group of one or

more bids from the same bidder, in which the time

interval between any two consecutive bids is below

a threshold θ

ses

. The session delimits activity inter-

vals for each bidder. The sequence is a group of one

or more sessions, where the inactivity period between

two consecutive sessions is below a threshold θ

seq

Notice that θ

ses

≤ θ

seq

. Each auction is modeled by a

group of sequences and the market is theset of all auc-

tions. In Figure 2, the labels T 1 and T 3 represent the

beginning of two auctions, and the end is deﬁned by

T 2 and T 4. In the case study presented in this work,

we adopt θ

ses

and θ

seq

as 90 minutes. We choose this

threshold after an analysis of the inter-bidding time of

the auctions.

Table 1 shows our proposed characterization cri-

teria for sequences and sessions. According to this

sequence characterization, there are 15 valid combi-

nations to describe patterns of auction’s sequences.

Considering the session’s characterization, there are

32 valid patterns. In order to simplify the sequence

and session patterns representation, we adopt letters

(minuscule or capital) as labels, such as the sequence

pattern IZW (initial sequences, with zigzag compe-

tition and winner changing) and the session pattern

OStrW (session with one bid, serial competition, non-

trigger, non-recurrent, and winner changing). It is im-

portant to emphasize that each criterion of sequence

(e.g., Time-Locality) and session (e.g., Size) is mutu-

ally exclusive.

The next section presents a case study that applies

this characterization model to actual data.

4 CASE STUDY: eBAY

This section presents our case study. We apply

our model to an actual dataset that consists of 8855

eBay auctions comprising of 85803 bids for Nin-

WEBIST 2007 - International Conference on Web Information Systems and Technologies

Table 1: Description of Auction Model Hierarchy- Sequences and Sessions.

Time-Locality

Initial (I) It is the ﬁrst sequence of the auction.

Intermediary (M) It is an intermediary sequence of the auction.

Final (F) It is the last sequence of the auction.

No competition (N) The sequence does not present competition, only one

bidder’s session.

Sequence Competition Successive competition (S) Exists a competition, but there is no overlap between

bidders’ actions.

Zigzag competition (Z) Characterizes a more direct competition, where one or

more bidders compete with each other in more than one

occasion in the sequence.

Winner’s Impact

Do not change winner (w) The sequence does not change the last winner bidder.

Change winner (W) The sequence changes the last winner bidder.

Size

One (O) The session has just one bid.

More (M) The session has more than one bid.

Competition

Serial (S) The session does not overlap with any other one.

Parallel (P) The session is concurrent with other(s), deﬁning a par-

allelism.

Session

Activity

Non-Trigger (t) The session does not initiate the sequence’s activity.

Trigger (T) The session initiates the sequence’s activity .

Recurrence

Non-Recurrent (r) The session is from a bidder who has not bid before in

this auction.

Recurrent (R) The session is from a bidder who has already bid in this

auction.

Winner’s Impact

Do not change winner (w) The session does not change the last winner bidder.

Change winner (W) The session changes the last winner bidder.

tendo GameCubes from 05/25/ 2005 to 08/15/2005.

eBay (EBay, 2005; Anderson et al., 2004; Bajari and

Hortacsu, 2003) employs a non-trivial mechanism of

second price auction, hidden winner, and hard auction

closing, in a typical complex online auction environ-

ment that demands characterization models that allow

more detailed analysis.

A statistical study of this dataset ﬁnds that the

number of distinct sellers is high (5453), which shows

that auctions are not concentrated among a small

number of sellers. The number of distinct bidders is

also high (18073), indicating high level of competi-

tion. On the other hand, from this set of bidders, just

very few of them become winners (735); the mean

variation of price between new and used products is

small, however the standard deviation of the prices is

very high; and there is a signiﬁcant number of average

bids per auctions (11.59), which suggests the level of

competition during the negotiation. This is conﬁrmed

by the average number of unique bidders per auction,

which is greater than 5.

Table 2 presents some auction information that is

important to better understand its dynamics. From

the original dataset, we consider auctions with bids

that achieve success in the negotiation, selling the

item. This group represents 75.7% of the complete

dataset. We can see that the average number of ses-

sions per sequence is small, just 1.53, since it is com-

mon to ﬁnd one or more sequences with one session

in all auctions. On the other hand, the average num-

ber of sequences per auction shows that the dynamics

of the negotiation is rich, which motivates our analy-

sis. Another aspect we analyze is the active and inac-

tive times of the auctions. The active time is the total

time during which the auction has activity, that is the

sum of the sequence times. We expected a short active

time per auction, since there are usually long intervals

between sets of bids, but an active time of just 1.72%

is beyond our expectations.

According to our characterization model, each

auction is composed by a set of one or more se-

quences, therefore we can describe each of them as a

distribution of sequence patterns, that is, a frequency

of occurrence of each valid sequence pattern (see Ta-

ble 1). For example, if an auction has four sequences,

from which two of them are IZW and the other two

are ISw, then this auction is represented by 50% of

IZW, 50% of ISw and 0% of other sequence patterns.

Amongst the diversity of auctions observed in our

dataset, some of them exhibit similar distribution of

sequence patterns. To analyze the auction negotia-

tion patterns in our case study, we use a data min-

ing technique called clustering (Bock, 2002) which

partitions the analyzed data into clusters of similar

data. More speciﬁcally we use the clustering algo-

rithm k-means (Hartigan, 1975). This type of algo-

ANALYZING EBAY NEGOTIATION PATTERNS

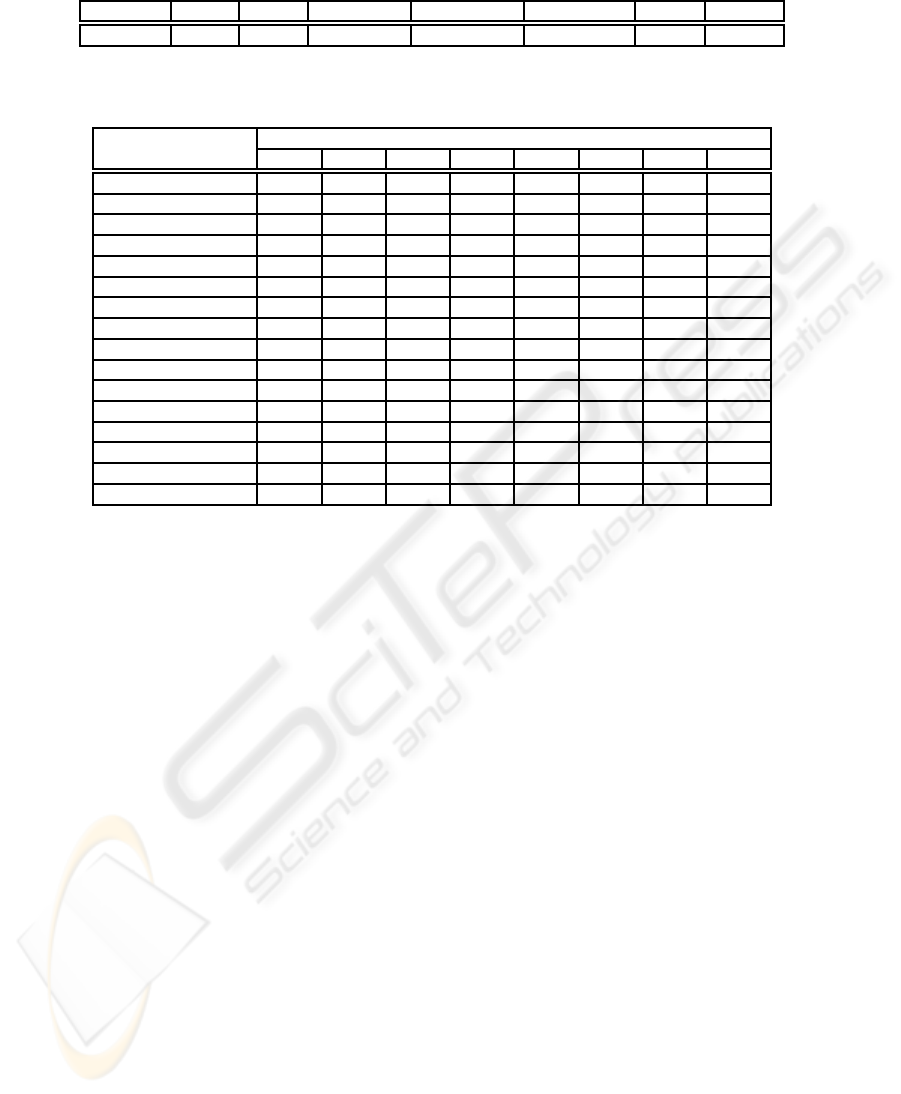
Table 2: Auction Characterization - General Statistics.

Auctions #Seq #Ses #(Ses/Seq) #(Seq/Auct) #(Ses/Auct) T

act

inact

6707 29575 45201 1.53 4.41 6.74 1.72% 98.28%

Table 3: Distribution of Cluster’s Sequences.

Sequence Patterns Clusters

0 1 2 3 4 5 6 7

1 (I-N-W) 17.53 0.00 18.28 0.00 47.19 0.00 0.00 21.61

2 (I-S-W) 0.12 12.85 0.19 0.00 0.00 44.74 0.00 0.02

3 (I-Z-W) 0.04 6.15 0.10 8.76 0.00 0.00 0.87 0.07

4 (M-N-w) 8.77 14.77 37.45 0.00 0.00 1.42 0.00 8.71

5 (M-S-w) 1.31 1.49 2.01 0.00 1.04 0.44 0.00 1.18

6 (M-Z-w) 0.08 0.07 0.08 0.00 0.00 0.00 0.00 0.00

7 (M-N-W) 43.10 24.12 14.99 0.00 1.15 2.94 0.00 12.65

8 (M-S-W) 7.91 13.99 5.22 0.00 0.00 3.59 0.00 31.15

9 (M-Z-W) 3.47 3.39 3.13 0.00 3.44 2.12 0.00 2.90

10 (F-N-w) 2.20 2.97 3.67 0.00 10.32 5.99 0.00 2.71

11 (F-S-w) 0.82 1.11 0.94 0.00 1.62 2.67 0.00 1.09

12 (F-Z-w) 0.13 0.15 0.12 0.00 0.32 0.44 0.00 0.33

13 (F-N-W) 5.02 3.58 4.89 0.00 16.57 11.90 99.13 5.21

14 (F-S-W) 5.66 4.97 5.28 91.24 11.72 13.94 0.00 6.92

15 (F-Z-W) 3.86 10.39 3.67 0.00 6.63 9.80 0.00 5.45

Frequency (%) 22.90 7.53 16.25 1.45 11.70 4.56 18.75 16.85

rithm is a technique well known to partition a het-

erogeneous group of entities (in the case, online auc-

tions) into clusters that have similar characteristics.

In our case study, we want to determine clusters of

auctions that present the same probability distribution

of sequence patterns. The ideal number of clusters is

determined through β-CV, as described in (Menasc´e

and Almeida, 2000; Menasc´e; et al., 1999). In our

datasets we found eight clusters.

Table 3 shows the probability distribution of se-

quences for the clusters. We have the frequency of oc-

currence for each of the 15 sequence patterns and also

the percentage of auction in each group (the last row

of the table). This result is very interesting, showing

different negotiation patterns for each group of auc-

tions. We can describe each cluster as:

• cluster 0: represents auctions with a high number

of sequences with the presence of initial (I), in-

termediary (M) and ﬁnal (F) patterns. They have

only 23.5% of competition, divided in 2/3 of suc-

cessive and 1/3 of zigzag competition. Almost

87% of sequences change the winner.

• cluster 1: consists of auctions with high activ-

ity, high level of competition (54.5%) from which

37% is zigzag type. Almost 80% of the auction

sequences changes the winner.

• cluster 2: group of auctions with a large num-

ber of sequences, but with low competition level

(20.7%). It is similar to cluster 0, however the

number of sequences that changes the winner is

much smaller, just 55.7%.

• cluster 3: represents auctions with predominance

of low levelof activity (sequences). Most auctions

in this cluster have just one sequence. The com-

petition level is maximum, with 91.2% of succes-

sive and 8.8% of zigzag competition types. As

expected , all sequences change the winner.

• cluster 4: consists of auctions with medium level

of activity, most of them with two activity mo-

ments. Most sequences do not present competi-

tion (75.2%) but change the winner (86.7%).

• cluster 5: a set of auctions with similar character-

istics of cluster 4 in terms of number of auction

sequences and winner changing. However these

auctions present a high competitionlevel (77.7%),

from which 85% is successive.

• cluster 6: group of auctions with very small num-

ber of sequences, almost all of them unique and

with no competition. All of them change the win-

ner, as expected, once the ﬁrst sequence always

changes the winner in eBay.

• cluster 7: has auctions with high activity, a sig-

niﬁcative amount of competition (49%), with pre-

dominance of successive type (8 in each 10 se-

quences with competition). Moreover, 86% of

WEBIST 2007 - International Conference on Web Information Systems and Technologies

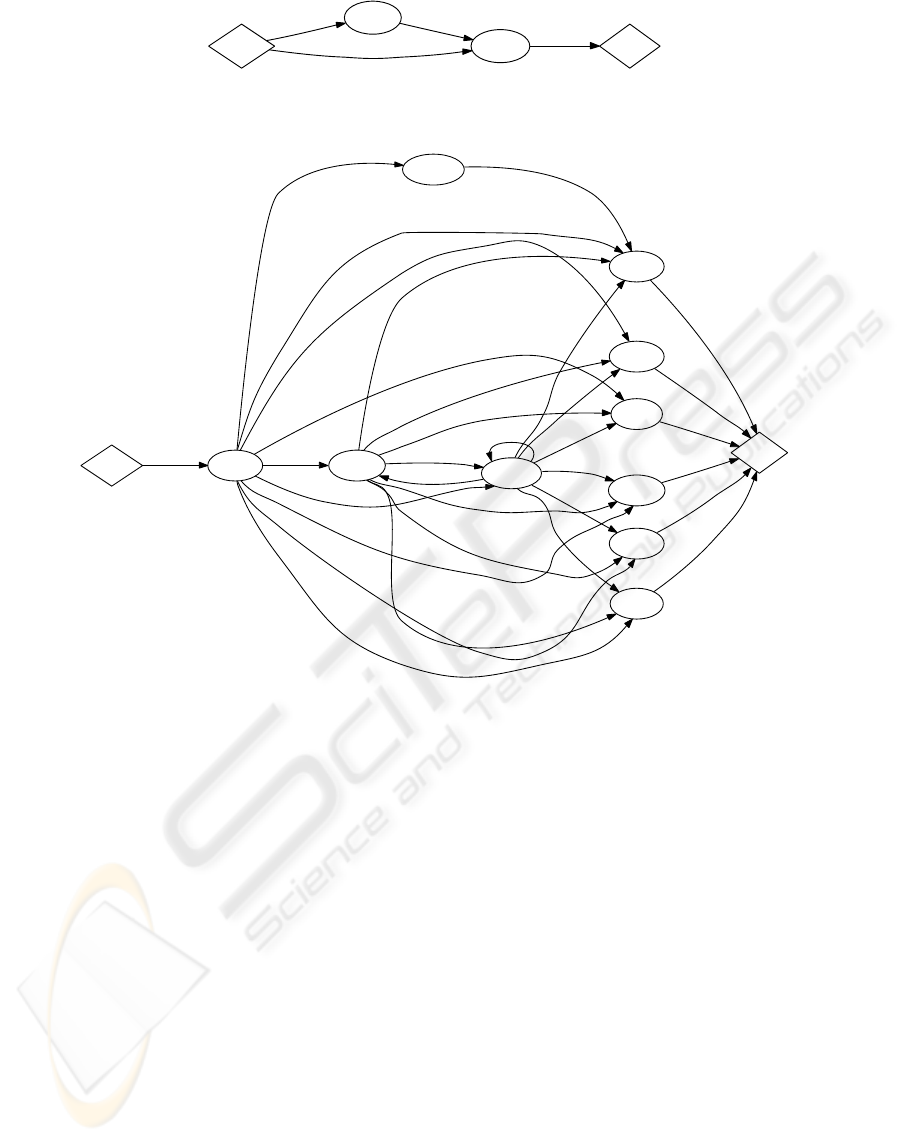
start

I-Z-W

0.1753

F-S-W

0.8247

end

1.0000

Figure 3: AMG - cluster 3.

start I-N-W

1.0000

end

M-S-w

0.0306

M-N-W

0.0344

M-Z-W

0.1006

F-N-w

0.1707

F-S-w

0.0293

F-Z-w

0.0038

F-N-W

0.3146

F-S-W

0.2025

F-Z-W

0.1134

0.0400

0.1600

0.0800

0.0400

0.2800

0.3200

0.0800

1.0000

0.0120

0.0361

0.1325

0.0241

0.1566

0.3614

0.2530

1.0000

Figure 4: AMG - cluster 4.

auction sequences changes the winner.

Table 4 shows some important aspects about auc-

tions for each cluster. It presents two auction negotia-

tion inputs and four outputs. AVG means the average

value of the attribute. This is an example of the re-

activity analysis introduced in Figure 1, in which we

start to explore the relationships between inputs and

reactivity and between reactivity and outputs. Cluster

1 has the lowest starting price, the highest duration,

and the highest 2nd price, that represents the auction

winner price in eBay. It is interesting to emphasize

that cluster 1 presents high competition level and ac-

tivity. Cluster 3 has an average duration of 5 days and

an average starting price of US$41.32. In these set of

auctions we identify very low activity and high com-

petition level. The mean number of bids is only 5 (as-

sociated to 3 bidders). This cluster has the lowest 2nd

price, that can be explained in part by its low activity,

that occurs mainly at the end of the negotiation. Clus-

ters 4 and 5 have similar characteristics, but different

behavior in terms of competition proﬁle, as previous

explained. However it is very interesting to note that

they produce different results: the average number of

bids and bidders for cluster 4 are almost half of the

cluster 5, which can be explained by the competition

level. Moreover, the ﬁnal negotiation price is almost

10% higher for auctions of cluster 5. Cluster 6 has

the highest starting price and the shortest duration,

that are negotiation inputs. In terms of its dynamics,

we previously identiﬁed low activity and competition.

However, it is interesting to note that these auctions

achieve a high winner price (the AVG 2nd price is

US$71.99). These can be explained by the fact that

these auction’s sellers set a very high starting price,

very close to the ﬁnal price obtained. It is important to

emphasize that we do not exhaust the inumerous pos-

sibilities of analysis, however these preliminar analy-

sis shows how interesting and promising is our novel

ANALYZING EBAY NEGOTIATION PATTERNS

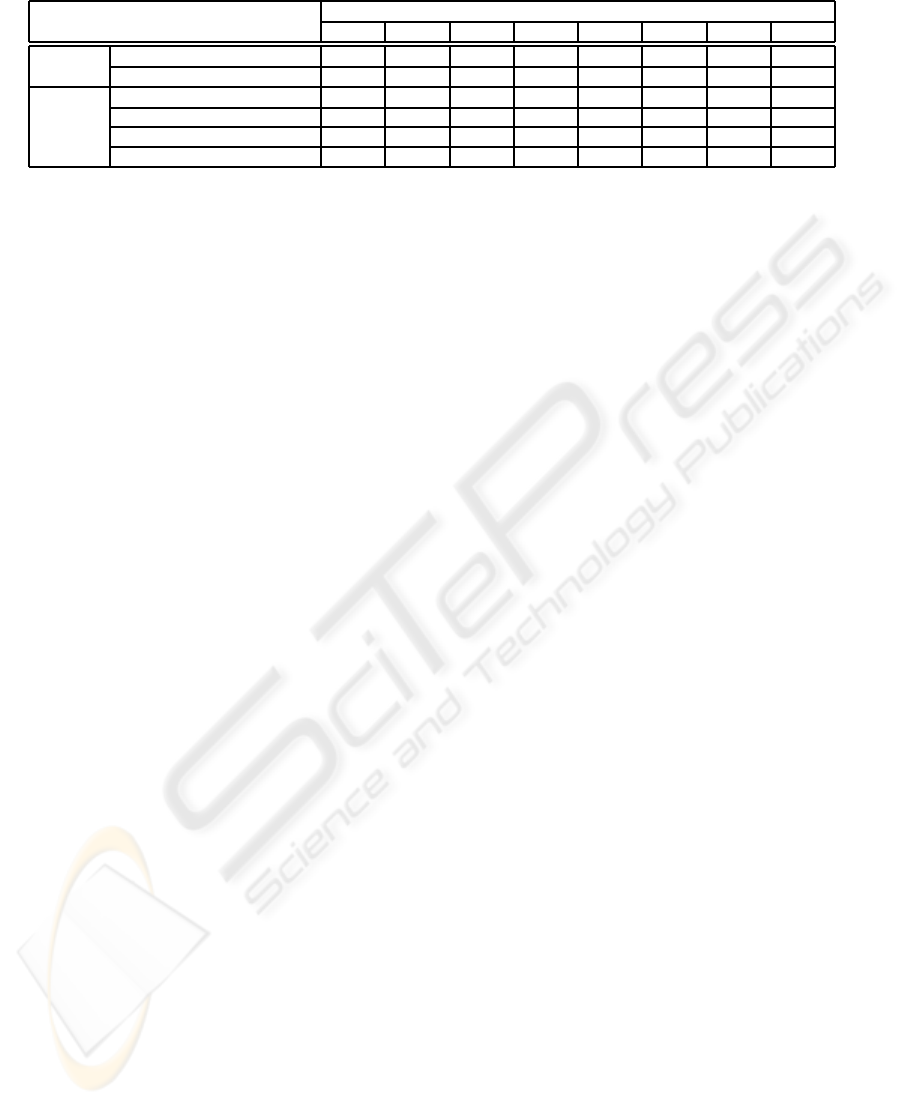
Table 4: AMG analysis.

Clusters

Aspects 0 1 2 3 4 5 6 7

Inputs

AVG Starting Price (US$) 18.78 11.91 17.39 41.32 46.92 38.55 71.4 20.27

AVG Duration (days) 5.9 4.8 5.8 5 4.9 4.5 2.7 5.3

Outputs

AVG #Bids 16.75 19.76 15.29 5.04 5.15 9.21 1.16 16.07

AVG #Bidders 7.35 8.34 6.88 2.98 2.87 4.78 1.05 7.48

AVG 1st Price (US$) 81.21 82.29 82.22 55.31 65.02 68.05 72.2 74.12

AVG 2nd Price (US$) 79.32 80.62 79.68 54.3 60.67 66.09 71.99 72.33

work.

The frequency distribution of sequence patterns

allow us to understand the overall auction negotia-

tion patterns, however it is not possible to analyze

the temporal aspects of the negotiation, that is, how

the auction develops across time. This aspect is im-

portant to complement the analysis and also to al-

low the possibility to generate an online auction syn-

thetic workload. In order to provide a way to do

this complementary analysis, for each identiﬁed clus-

ter of auctions, we create an Auction Model Graph

(AMG). AMG, that is based on Customer Behavior

Model Graph (CBMG) (Menasc´e and Almeida, 2000;

Menasc´e; et al., 1999). This is a state transition graph

that has one node for each possible sequence pat-

tern and the edges are transitions between these se-

quences. A probability is assigned to each transi-

tion between two nodes, representing the frequency

at which these two sequences occur consecutively in

a cluster.

Due to lack of space we present in this paper only

two AMGs, to illustrate the usefulness of this ap-

proach and as the wealth of details that it provides.

Figures 3 and 4 show the AMG of clusters 3 and 4,

respectively.

The AMG presented in Figure 3 is very simple.

In this cluster, 17.53% of the initial sequences of

the auction is represented by zigzag competition and

they are succeeded by ﬁnal sequences with successive

competition. The other group denotes auctions with

unique sequences of type F-S-W.

The AMG of Figure 4 is more complex than the

previous AMG and through its analysis it is possi-

ble to understand details of the auction negotiation

pattern. We can realize that there is not any auc-

tion with unique sequence and that all of them be-

gins with the sequence pattern I-N-W. About 83% of

the auctions from this group has a second period of

activity where the negotiation determines the end of

the auction. In these auctions sequences, 49% has al-

ready deﬁned their winners in the initial activity pe-

riod while 51% has determined the winner in the last

auction’s sequence. The other 17% of auctions haveat

least one more intermediary sequence before the auc-

tion resumes. Moreover, it is interesting to note that

the competition arises at the end of the auctions (ﬁnal

sequences), where we observe 43% of competitivese-

quences and the predominance of zigzag competition

type.

As we can see, the details presented in these

graphs are so rich, and through them its possible to

model an online auction workload and design new

service personalization policies.

This analysis is an example of how our model can

help the understanding of the auction dynamics and is

the basis for reactivity modeling, as we explained in

Section 1.

The application of our characterization model to

an eBay dataset demonstrates that our proposal pro-

vides a way to open the auction dynamics’s “black

box”. We are aware that these results must be val-

idated against a larger dataset and realize that we

should characterize auctions using sequences, and

bidders through sessions. By doing this, we will have

a better semantic characterization, since the current

work shows that it is difﬁcult to explain some speciﬁc

behavior through a general data analysis. In the next

section we present our conclusion and ongoing work.

5 CONCLUSION

This work presents a new hierarchical characteriza-

tion model for online auctions, which provides novel-

ties in order to model and understand the factors that

characterize and explain the auction dynamics, differ-

ently of other characterizationmodels (Roth and Ock-

enfels, 2002; Bapna et al., 2004; Easley and Tenorio,

2004). Moreover, we apply this model to an actual

dataset that consists of 8855 eBay auctions, showing

the advantages of our model in order to discover the

online auction negotiation patterns.

Applying a data mining technique called cluster-

ing, which sorts the analyzed data into clusters of sim-

ilar data, we found out eight clusters in our datasets.

This result is very interesting, showing different ne-

WEBIST 2007 - International Conference on Web Information Systems and Technologies

gotiation patterns for each group of auctions consid-

ering not only static and aggregated measures, but the

auction dynamics, a novelty for online auctions re-

search. We also introduce the Auction Model Graph

(AMG) to analyze the temporal aspect of the nego-

tiation. This aspect is important to complement the

analysis and can also be used to generate an online

auction synthetic workload.

This work is part of our ongoing research to ana-

lyze reactivity in e-business. We hope that, by under-

standing the reactivity patterns in relation to the ne-

gotiation features and speciﬁc business rules that gov-

ern the auction environment, we will be able to con-

ceptualize and design a comprehensive framework to

model reactivity. Also, studying reactivity may bene-

ﬁt the economicanalysis of Web-based environments,

such as marketplaces.

As future work we are going to characterize the

bidders. Characterizing both bidders and auctions

will allow us to conduct in-depth analysis of reactivity

patterns that emerge in auction negotiations.

REFERENCES

Achtert, E., Kriegel, H., Pryakhin, A., and Schubert,

M. (2005). Hierarchical density-based clustering

for multi-represented objects. In First International

Workshop on Mining Complex Data MCD, Houston,

Texas. IEEE.

Anderson, S., Friedman, D., Milam, G., and Singh, N.

(2004). Seller strategies on ebay. Industrial Orga-

nization 0412004, Economics Working Paper Archive

EconWPA.

Ariely, D. and Simonson, I. (2003). Buying, bidding, play-

ing, or competing? value assessment and decision dy-

namics in online auctions. Journal of Consumer Psy-

chology, 13(1):113–123.

Bajari, P. and Hortacsu, A. (2003). The winner’s curse,

reserve prices, and endogenous entry: Empirical in-

sights from ebay auctions. RAND Journal of Eco-

nomics, 34(2):329–55.

Bapna, R., Goes, P. B., and Gupta, A. (2003). Replicat-

ing online yankee auctions to analyze auctioneers’ and

bidders’ strategies. Information Systems Research,

14(3):244–268.

Bapna, R., Goes, P. B., Gupta, A., and Jin, Y. (2004).

User heterogeneity and its impact on electronic auc-

tion market design: An empirical exploration research

essays. MIS Quarterly, 28(1).

Bock, H.-H. (2002). Data mining tasks and methods - clas-

siﬁcation: the goal of classiﬁcation. pages 254–258.

Chakravarti, D., Greenleaf, E. A., Sinha, A., Cheema, A.,

Cox, J. C., Friedman, D., Ho, T. H., Isaac, R. M.,

Rapoport, A. A. M. A., Rothkopf, M. H., Srivastava,

J., and Zwick, R. (2002). Auctions: Research oppor-

tunities in marketing. Marketing Letters, 13(3):279–

293.

Chelcea, S., Silva, A. D., Lechevallier, Y., Tanasa, D., and

Trousse, B. (2005). Pre-processing and clustering

complex data in e-commerce domain. In First Inter-

national Workshop on Mining Complex Data MCD,

Houston, Texas. IEEE.

Easley, R. F. and Tenorio, R. (2004). Jump bidding strate-

gies in internet auctions. Manage. Sci., 50(10):1407–

1419.

EBay (2005). eBay, Inc. http://www.ebay.com/.

Gilkeson, J. H. and Reynolds, K. (2003). Determinants

of internet auction success and closing price: An ex-

ploratory study. Psychology & Marketing, 20(6):537–

566.

Hartigan, J. (1975). Clustering Algorithms. John Wiley and

Sons, Inc.

Lucking-Reiley, D. (1999). Using ﬁeld experiments to test

equivalence between auction formats: Magic on the

internet. American Economic Review, 89(5):1063–

1080.

Melnik, M. I. and Alm, J. (2002). Does a seller’s e-

commerce reputation matter? evidence from ebay

auctions. Journal of Industrial Economics, 50(3):337–

349.

Menasc´e, D. A. and Almeida, V. A. F. (2000). Scaling for

E Business: Technologies, Models, Performance, and

Capacity Planning. Prentice Hall PTR, Upper Saddle

River, NJ, USA.

Menasc´e;, D. A., Almeida, V. A. F., Fonseca, R., and

Mendes, M. A. (1999). A methodology for work-

load characterization of e-commerce sites. In EC ’99:

Proceedings of the 1st ACM conference on Electronic

commerce, pages 119–128, New York, NY, USA.

ACM Press.

Pereira, A., Franco, G., Silva, L., Meira, Jr., W., and Santos,

W. (2004). The USAR characterization model. In Pro-

ceedings of the IEEE 7th Annual Workshop on Work-

load Characterization (WWC-7), Austin, Texas, USA.

IEEE Computer Society.

Pereira, A., Mourao, F., Goes, P., and Meira, Jr., W. (2006a).

Reactivity in online auctions. In et al., T. G., edi-

tor, Workshop Reactivity on the Web at the Interna-

tional Conference on Extending Database Technol-

ogy - EDBT 2006, volume 4254 of Lecture Notes

in Computer Science, pages 909–918, Munich, Ger-

many. Springer.

Pereira, A., Silva, L., Meira Jr., W., and Santos, W. (2006b).

Assessing the impact of reactive workloads on the per-

formance of web applications. In ISPASS-2006: IEEE

International Symposium on Performance Analysis of

Systems and Software, Austin, TX, USA. IEEE Com-

puter Society.

Roth, A. and Ockenfels, A. (2002). Last-minute bidding

and the rules for ending second-price auctions: Evi-

dence from ebay and amazon auctions on the internet.

American Economic Review, 92(4):1093–1103.

ANALYZING EBAY NEGOTIATION PATTERNS