
Efficient Interpretation of Large Quantifications in a
Process Algebra
Beno
ˆ
ıt Fraikin and Marc Frappier
GRIL, D
´
epartement d’informatique, Universit
´
e de Sherbrooke,
2500, Boulevard de l’universit
´
e, Sherbrooke, Qu
´
ebec, Canada J1K 2R1
Abstract. The process algebra interpreter EB
3
PAI supports the EB
3
method,
which was developed for the purpose of automating the development of infor-
mation systems through code generation and efficient interpretation of abstract
specifications. For general information system patterns, EB
3
PAI executes in linear
time with respect to the number of terms and operators in the process expression
and in logarithmic time with respect to the number of entities in the system. This
paper described three optimization techniques of EB
3
PAI.
1 Introduction
The EB
3
PAI project is part of the APIS research project [1], whose objective is to de-
velop a case tool that generates executable information systems (IS) from formal spec-
ifications (abstract models). In traditional IS development, the bulk of the design, pro-
gramming and testing is done manually by humans. These three activities consume up
to 70% of the development effort. They are usually not hard to accomplish, but they are
time-consuming and error-prone. The key to reducing development costs and increas-
ing quality clearly resides in eliminating or mechanizing these three tasks. The EB
3
method was developed for the purpose of automating the development of IS through
code generation and efficient specification interpretation. Designed by Frappier and St-
Denis [2], the EB
3
language includes a process algebra to support an event-oriented
specification style. Initial work led to a practical set of rules for an interpreter of EB
3
process expressions [3], called EB
3
PAI. This paper describes the last step in efficiently
implementing this interpreter.
2 The EB
3
Specification Method
The EB
3
method [2] has been specifically created to specify information systems. It
relies on event-oriented specification notations like CSP, CCS and LOTOS. However,
special features have been added to take the specificities of information systems into
account. The input behavior of the system is defined by the process expression main.
Each execution of an action (an input) generates a response (an output). The denota-
tional semantics of EB
3
is given by a relation R between the traces accepted by main
and the set of output events. A process expression is recursively defined over a set of
Fraikin B. and Frappier M. (2006).
Efficient Interpretation of Large Quantifications in a Process Algebra.
In Proceedings of the 4th International Workshop on Modelling, Simulation, Verification and Validation of Enterprise Information Systems, pages
189-192
DOI: 10.5220/0002500101890192
Copyright
c
SciTePress

symbols Σ, called the action set, λ (an internal action that denotes non-observable ac-
tivity of the system) and (which denotes a successful termination) in combination
with operators. Operators in EB
3
draw their inspiration from regular expressions, the
sequential composition (), the choice (|) and the Kleene closure (
∗
), with the addition
of some operators from CSP and LOTOS: synchronization, guard, process call, and
synchronization quantification (also called indexing in CSP). The symbol 9 denotes the
interleave operator, i.e., |[∅]| . EB
3
PAI also have a guard operator and process call. The
symbol PE denotes the set of all process expressions.
It is important to note that quantification is a crucial operator in IS specification.
This constitutes a major difference from other problem domains where process algebras
are typically used (protocol specification for example). Another difference is that EB
3
is only concerned by trace equivalence. Since the main aim of EB
3
is to provide an ex-
ecutable specification, the specification style used to achieve this goal is also different.
Frappier and St.-Denis in [2] have proposed a set of rules that give EB
3
its operational
behavior. EB
3
PAI executes a specification by simply evaluating the inference rules. We
do not generate code per se; EB
3
PAI can be considered as a virtual machine and each
specification becomes a high-level program. The implementation is the combination of
EB
3
PAI and the specification.
3 Dynamic Optimization in the EB
3
PAI Interpretation Process
In [3] we provide some static optimizations. However, this is not sufficient to yield
efficient interpretation. To provide a useful tool, we need to optimize other aspects of
the interpretation algorithm, primarily to reduce the time and space complexity for large
quantifications.
3.1 Optimization of Process Expression Storage in Memory
During an execution, actions and process expressions can be copied several times. Some
execution sequences can require a large amount of memory. The two main causes are
quantification and choice resulting in the execution of some non-deterministic specifi-
cations. In order to minimize memory space, process expressions can be represented by
a graph which allows them to be shared. For instance, if E
1
is a sub-expression of both
E
2
and E
3
, than E
1
can be instantiated once and referenced by both E
2
and E
3
.
3.2 Optimizing Quantification Execution Time: Direct κ-optimization
The EB
3
language allows the use of quantification operators. A basic approach to ex-
ecuting quantification operators is too ineffective to be acceptable. To optimize these
executions, we determine by static analysis of each quantified expression which value
of the quantified set must be selected based on the parameters of the action to exe-
cute. We call these values κ-values, the positions of the values in the action parameters
κ-positions, and this method direct κ-optimization.
This approach is sufficient to optimize a choice quantification, since the quantifica-
tion disappears after the transition. In the case of a quantified interleave, the quantifica-
tion remains in the result process expression, since it can spawn one interleave process
190

for each value in the quantification set. The interleave of the instantiated process ex-
pressions is represented by a function K : T → PE such that K(Π(σ)) is the only
process expression that can execute σ.
3.3 Extending Quantification Optimization: Indirect κ-optimization
We have found conditions under which a quantification can be optimized when the
algorithm used for the direct κ-optimization fails to find a single κ-position for each
action. We can summarize the general idea of indirect κ-optimization, as follows:
During static analysis :
1. Find the quantified choice operators to deduce the possible functional depen-
dencies (below we refer to choice quantified variables occurring in the scope
of other quantifications (interleave or choice) as the dependent variables and
the enclosing quantified variables as the keys).
2. For all actions not optimized with the algorithm of the κ-optimization: identify
the producer that binds the keys (bId in the example) to the dependent vari-
able (mId in the example) under the condition that the choice and interleave
quantifications to optimize are synchronized on these actions.
At runtime :
1. When a producer is executed, store the value of the functional dependency
between the set of keys and the dependent variable.
2. Store the value of the new process expression for the operand of the quantified
interleave in a mapping K, as for direct κ-optimization.
3. When a consumer is executed, delete the stored value of the functional depen-
dency between the keys and the dependent variable.
Complete κ-optimization is not effective for all specifications that can be written.
Actually, it is not effective for all IS specifications. However, our aim is to optimize
all specifications written with the patterns described in [2]. We have established that
the following patterns satisfy the conditions for κ-optimization: the producer-modifier-
consumer, the one-to-many association, the multiple (many-to-many) association, the
n-ary association, the weak entity type, the recursive association, and the inheritance
association.
4 Implementation and Performance
Complexity analysis Let n denote the sum of all |X|, where X is either an entity type
or an association of an EB
3
specification. Let s denote the number of nodes in the tree
representing a process expression, excluding the nodes of a κ-optimized quantifica-
tion (they will be computed with n). Note that for most ISs, s is usually small (e.g.,
s ≪ 10
3
), whereas n can be quite large (e.g., n ≪ 10
12
). Figure 1 summarizes the al-
gorithmic and the space complexity of the K-optimization and compares them with no
optimization in EB
3
PAI and with manual implementation (i.e.. outside EB
3
PAI). Thus,
for κ-optimizable specifications, EB
3
PAI has an overhead of O(s) compared with man-
ual implementation of an IS. With no κ-optimization, the difference is substantial and
EB
3
PAI becomes impractical as a tool, but it can still be useful for specification anima-
tion for validation purposes.
191
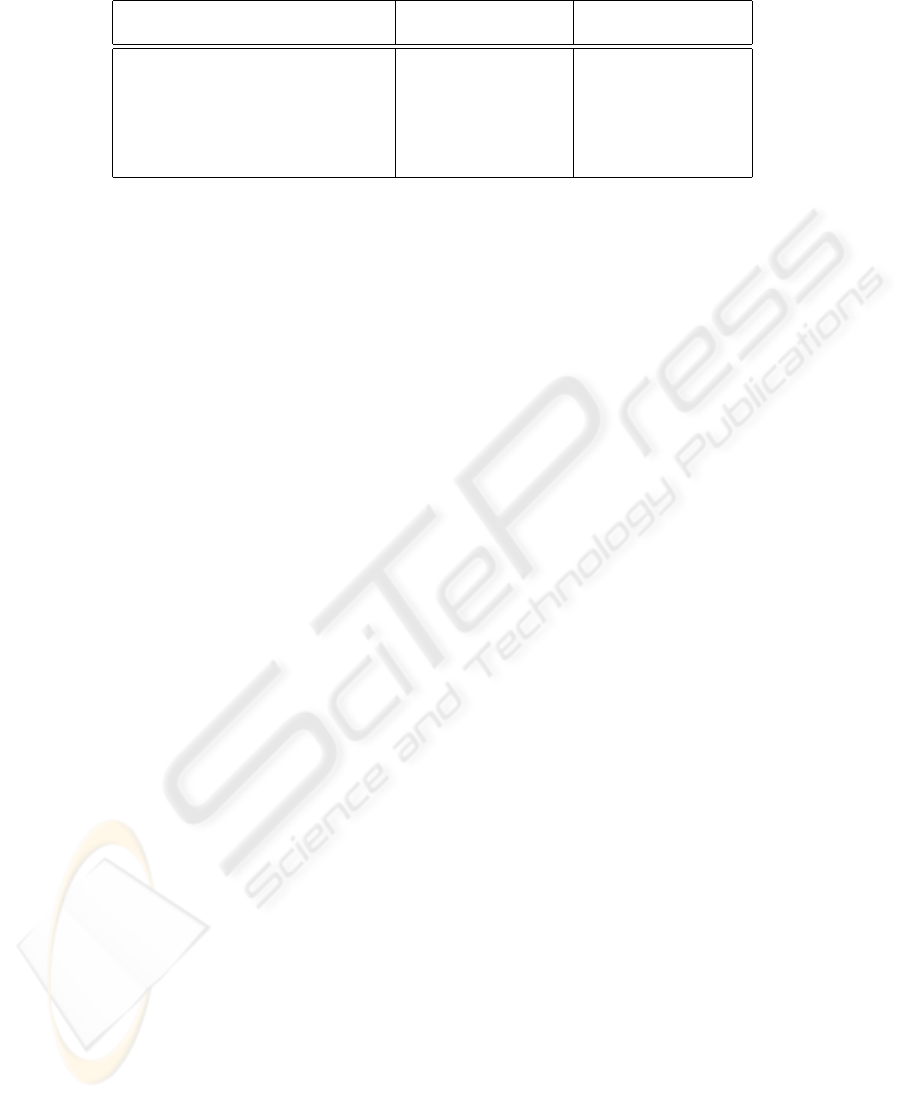
Alg. complexity Space complexity
no optimization O(s.n) O(n + s)
direct κ-optimization O(log(n) + s) O(n + s)
indirect κ-optimization O(log(n) + s) O(n + s)
manual implementation O(log(n)) O(n)
Fig.1: Algorithmic and space complexity of EB
3
PAI.
Performance for direct κ-optimization Complete κ-optimization is not implemented,
but direct κ-optimization is. The performance for indirect κ-optimization should be
very close to that of direct κ-optimization, because it uses the same data structures
plus an additional hash table to store the functional dependencies. Performance tests
were conduct with a specification of a library management system on a Pentium III
800MHz with 384Mo of SDRAM, running GNU/Linux. Indirect κ-optimization has not
been implemented yet; only direct κ-optimization. The transaction mean time of valid
actions is 97ms. Invalid actions (for which the execution failed) are less expensive in
time (approx. 40 ms per action) than valid actions. The same specification implemented
in Java using an Oracle database provides an average transaction processing time of
10 ms, which is 10 times faster than EB
3
PAI. Nevertheless, 100 ms is still acceptable for
many IS systems where the transaction rate is low (e.g., a library management system).
5 Conclusion
In this paper, we have presented two optimization techniques to efficiently execute
quantified process expressions in the EB
3
process algebra. Their space and algorithmic
complexities are comparable to those of a manual implementation for a large number
of IS specifications which are determined by a set of specification patterns. Direct k-
optimization was implemented in the EB
3
PAI interpreter. It performs 10 times slower
than a manual implementation of the specification for the library system, but its aver-
age response time is acceptable for a large class of IS with low transaction rates, which
demonstrates that abstract interpretation is a viable way of implementing IS.
References
1. Frappier, M., Fraikin, B., Laleau, R., Richard, M.: Automatic production of information sys-
tems. In: AAAI Symposium on Logic-Based Program Synthesis, Stanford University, Stan-
ford, CA (2002)
2. Frappier, M., St-Denis, R.: EB
3
: an entity-based black-box specification method for informa-
tion systems. Software and System Modeling 2 (2003) 134–149
3. Fraikin, B., Frappier, M.: Efficient execution of process expressions using symbolic interpre-
tation. Technical report 8, Universit
´
e de Sherbrooke, D
´
epartement d’Informatique, Qu
´
ebec,
Canada (2005)
192
