Multinomial Mixture Modelling

for Bilingual Text Classiﬁcation

Jorge Civera and Alfons Juan

Departament de Sistemes Inform

atics i Computaci

Universitat Polit

ecnica de Val

encia

46022 Val

encia, Spain

Abstract. Mixture modelling of class-conditional densities is a standard pat-

tern classiﬁcation technique. In text classiﬁcation, the use of class-conditional

multinomial mixtures can be seen as a generalisation of the Naive Bayes text clas-

siﬁer relaxing its (class-conditional feature) independence assumption. In this pa-

per, we describe and compare several extensions of the class-conditional multino-

mial mixture-based text classiﬁer for bilingual texts.

1 Introduction

Mixture modelling is a popular approach for density estimation in supervised and un-

supervised pattern classiﬁcation [1]. On the one hand, mixtures are ﬂexible enough for

ﬁnding an appropriate tradeoff between model complexity and the amount of training

data available. Usually, model complexity is controlled by varying the number of mix-

ture components while keeping the same (often simple) parametric form for all compo-

nents. On the other hand, maximum likelihood estimation of mixture parameters can be

reliably accomplished by the well-known Expectation-Maximisation (EM) algorithm.

Although most research on mixture models has concentrated on mixtures for con-

tinuous data, there are many pattern classiﬁcation tasks for which discrete mixtures are

better suited. This is the case of text classiﬁcation (categorisation) [2]. In this case, the

use of class-conditional discrete mixtures can be seen as a generalisation of the well-

known Naive Bayes text classiﬁer [3, 4]. In [5], the binary instantiation of the Naive

Bayes classiﬁer is generalised using class-conditional Bernoulli mixtures. Similarly,

in [6,7], its multinomial instantiation is generalised with multinomial mixtures. Both

generalisations seek to relax the Naive Bayes (class-conditional feature) independence

assumption made when using a single Bernoulli or multinomial distribution per class.

This unrealistic assumption of the Naive Bayes classiﬁer is one of the main reasons ex-

plaining its comparatively poor results in contrast to other techniques such as boosting-

based classiﬁer committees, support vector machines, example-based methods and re-

gression methods [2]. In fact, the performance of the Naive Bayes classiﬁer is signiﬁ-

cantly improved by using the generalisations mentioned above [5–7]. Moreover, there

are other recent generalisations (and corrections) that also overcome the weaknesses of

the Naive Bayes classiﬁer and achieve very competitive results [8–12].

In this paper, we describe and compare several (minor) extensions of the (class-

conditional) multinomial mixture-based text classiﬁer for the case in which text data

Civera J. and Juan A. (2006).

Multinomial Mixture Modelling for Bilingual Text Classiﬁcation.

In 6th International Workshop on Pattern Recognition in Information Systems, pages 93-103

DOI: 10.5220/0002471900930103

 SciTePress

is available in two languages. Our interest in this task of bilingual text classiﬁcation

comes from its potential use in statistical machine translation. In this application area,

the problem of learning a complex, global statistical transducer from heterogeneous

bilingual sentence pairs can be greatly simpliﬁed by ﬁrst classifying sentence pairs

into homogeneous classes and then learning simpler, class-speciﬁc transducers [13].

Clearly, this is only a marginal application of bilingual text classiﬁcation. More gen-

erally, the proliferation of multilingual documentation in our Information Society will

surely attract many research efforts in multilingual text classiﬁcation. Obviously, most

conventional, monolingual text classiﬁers can be also extended in order to fully exploit

the intrinsic redundancy of multilingual texts.

The following section describes the different basic models we consider for multino-

mial mixture modelling of bilingual texts. In section 3, we brieﬂy discuss how to plug

these basic models in the Bayes decision rule for bilingual classiﬁcation. Section 4

poses the maximum likelihood estimation of these models using the EM algorithm. Fi-

nally, section 5 will be devoted to experimental results and section 6 will discuss some

conclusions and future work.

2 Multinomial Mixture Modelling

A ﬁnite mixture model is a probability (density) function of the form:

p(x) =

i=1

p(x | i) (1)

where I is the number of mixture components and, for each component i, α

∈ [0, 1]

is its prior or coefﬁcient and p(x | i) is its component-conditional probability (density)

function. It can be seen as a generative model that ﬁrst selects the ith component with

probability α

and then generates x in accordance with p(x | i).

The choice of a particular functional form for the components depends on the type

of data at hand and the way it is represented. In the case of the bag-of-words text repre-

sentation, the order in which words occur in a given sentence (or document) is ignored;

the only information retained is a vector of word counts x = (x

, . . . , x

), where x

is the number of occurrences of word d in the sentence, and D is the size of the vo-

cabulary (d = 1, . . . , D). In this case, a convenient choice is to model each component

i as a D-dimensional multinomial probability function governed by its own vector of

parameters or prototype p

= (p

, . . . , p

) ∈ [0, 1]

p(x | i) =

d=1

(2)

where x

is the sentence length. Equation (1) in this particular case is called

multinomial mixture. Note that the ﬁrst factor in (2) is a multinomial coefﬁcient giving

the number of different sentences of length x

that are equivalent in the sense of having

identical vector of word counts x. Also note that p

is the ith component-conditional

probability of word d to occur in a sentence and, therefore, the second factor in (2)

is the probability that each of these equivalent sentences has to occur. Thus, Eq. (2)

(and Eq. (1)) deﬁnes a explicit probability function over all D-dimensional vectors of

word counts with identical x

, and an implicit probability function over all sentences

of length x

in which equivalent sentences are equally probable.

In this work, we are interested in modelling the distribution of bilingual texts;

i.e. pairs of sentences (or documents) that are mutual translations of each other. Bilin-

gual texts will be formally described using a direct extension of the bag-of-words rep-

resentation of monolingual text. That is, we have pairs of the form (x, y) in which x is

the bag-of-words representation of a sentence in an input (source) language, and y is its

counterpart in an output (target) language. For instance, x and y may be bag-of-words

in Dutch and English, respectively. As above, x is a D-dimensional vector of words

counts. Regarding y, the size of the output vocabulary will be denoted by E, and thus

y is a E-dimensional vector of word counts y ∈ {0, 1, . . . , y

}

with y

e=1

For modelling the probability of a pair (x, y), we will consider ﬁve simple models:

1. Monolingual input-language model:

p(x, y) = p(x) (3)

where p(x) is given by (1) and (2).

2. Monolingual output-language model:

p(x, y) = p(y) (4)

where p(y) is a multinomial mixture model for the output bag-of-words,

p(y) =

i=1

p(y | i) with p(y | i) =

e=1

(5)

where q

is the ith component-conditional probability of word e to occur in an

output sentence.

3. Bilingual bag-of-words model:

p(x, y) = p(z) (6)

where z is a bilingual bag-of-words obtained from the concatenation of the sen-

tences originating (x, y), and p(z) is a monolingual, multinomial mixture model

like the two previous models.

4. Global (Naive Bayes) decomposition model:

p(x, y) = p(x) p(y) (7)

where p(x) and p(y ) are given by the ﬁrst two monolingual models above.

5. Local (Naive Bayes) decomposition model:

p(x, y) =

i=1

p(x, y | i) with p(x, y | i) = p(x | i) p(y | i) (8)

where p(x | i) is given by (2) and p(y | i) by (5).

Note that the ﬁrst two models ignore one of the languages involved and hence they

do not take advantage of the intrinsic redundancy in the available data. The remaining

manage bilingual data in slightly different ways.

3 Bilingual Text Classiﬁcation

As with other types of mixtures, multinomial mixtures can be used as class-conditional

models in supervised classiﬁcation tasks. Let C denote the number of supervised classes.

Assume that, for each supervised class c, we know its prior p

and its class-conditional

probability function, which is given by one of the ﬁve models discussed in the previous

section. Then, the Bayes decision rule is to assign each pair (x, y) to a class giving

maximum a posteriori probability or, equivalently,

c(x, y) = argmax

log p

+ log p(x, y | c) (9)

In the case of the monolingual input-language model, this rule becomes:

c(x, y) = argmax

log p

+ log

i=1

d=1

cid

(10)

Similar rules hold for the monolingual output-language model and the bilingual bag-of-

words model. In the case of the global decomposition model, it is

c(x, y) = argmax

log p

+ log

i=1

d=1

cid

+ log

i=1

e=1

cie

(11)

while, in the local decomposition model, we have

c(x, y) = argmax

log p

+ log

i=1

d=1

cid

e=1

cie

(12)

4 Maximum Likelihood Estimation

Let (X, Y ) = {(x

, y

), . . . , (x

, y

)} be a set of samples available to learn one of

the ﬁve mixture models discussed in section 2. This is a statistical parameter estimation

problem since the mixture is a probability function of known functional form, and all

that is unknown is a parameter vector including the priors and component prototypes.

In what follows, we will focus on the local decomposition model; the rest of models

can be estimated in a similar way.

The vector of unknown parameters for the local decomposition model is:

Θ = (γ

, . . . , γ

; p

, . . . , p

; q

, . . . , q

) (13)

We are excluding the number of components from the estimation problem, as it is a cru-

cial parameter to control model complexity and receives special attention in Section 5.

Following the maximum likelihood principle, the best parameter values maximise

the log-likelihood function

L(Θ|X, Y ) =

n=1

log

i=1

p(x

|i) p(y

|i) (14)

In order to ﬁnd these optimal values, it is useful to think of each sample pair (x

, y

)

as an incomplete component-labelled sample, which can be completed by an indica-

tor vector z

= (z

, . . . , z

) with 1 in the position corresponding to the component

generating (x

, y

) and zeros elsewhere. In doing so, a complete version of the log-

likelihood function (14) can be stated as

(Θ|X, Y,Z) =

n=1

i=1



log γ

+ log p(x

|i) + log p(y

|i)



(15)

where Z = {z

, . . . , z

} is the so-called missing data.

The form of the log-likelihood function given in (15) is generally preferred because

it makes available the well-known EM optimisation algorithm (for ﬁnite mixtures) [14].

This algorithm proceeds iteratively in two steps. The E(xpectation) step computes the

expected value of the missing data given the incomplete data and the current parameters.

The M(aximisation) step ﬁnds the parameter values which maximise (15), on the basis

of the missing data estimated in the E step. In our case, the E step replaces each z

the posterior probability of (x

, y

) being actually generated by the ith component,

p(x

| i) p(y

| i)

′

p(x

| i

′

) p(y

| i

′

)

(16)

for all n = 1, . . . , N and i = 1, . . . , I, while the M step ﬁnds the maximum likelihood

estimates for the priors,

n=1

(i = 1, . . . , I) (17)

and the component prototypes,

n=1

d=1

n=1

e=1

n=1

(18)

for all i = 1, . . . , I.

The above estimation problem and algorithm are only valid for a single multino-

mial mixture of the form (8). Nevertheless, it is straightforward to extend them in

order to simultaneously work with several class-conditional mixtures in a supervised

setting. In this setting, training samples come with their corresponding class labels,

{(x

, y

, c

)}

n=1

, and the vector of unknown parameters is:

Ψ = (p

, . . . , p

; Θ

, . . . , Θ

) (19)

where, for each supervised class c, its prior probability is given by p

and its class-

conditional probability function is a mixture controlled by a vector of the form (13),

. The log-likelihood of Ψ w.r.t. the labelled data is

n=1

log p

i=1

p(x

|i, c

)p(y

|i, c

) (20)

which can be optimised by a simple extension of the EM algorithm given above. More

precisely, the E step computes (16) using Θ

, while the M step computes the conven-

tional estimates for the class priors and (class-dependent versions of) Eqs. (17) to (18)

for each class separately. This simple extension of the EM algorithm is equivalent to the

usual practice of applying its basic version to each supervised class in turn. However,

we prefer to adopt the extended EM, mainly to have a uniﬁed framework for classiﬁer

training in accordance with the log-likelihood criterion (20).

5 Experimental Results

The ﬁve different models considered were assessed and compared on two bilingual

text classiﬁcation datasets (tasks) known as the Traveller dataset and the BAF corpus.

The Traveller dataset comprises Spanish-English sentence pairs drawn from a restricted

semantic domain, while BAF is a parallel French-English corpus collected from a mis-

cellaneous ”institutional” document pool. This section ﬁrst describes these datasets and

then provides the experimental results obtained.

5.1 Datasets

The Traveller dataset comes from a limited-domain Spanish-English machine transla-

tion application for human-to-human communication situations in the front-desk of a

hotel [15]. It was semi-automatically built from a small “seed” dataset of sentence pairs

collected from traveller-oriented booklets by four persons. Note that each person had to

cater for a (non-disjoint) subset of subdomains, and thus each person can be considered

a different (multimodal) class of Spanish-English sentence pairs. Subdomain overlap-

ping among classes foresees that perfect classiﬁcation is not possible, although in our

case, low classiﬁcation error rates will indicate that our mixture model has been able to

capture the multimodal nature of the data. Unfortunately, the subdomain of each pair

was not recorded, and hence we cannot train a subdomain-supervised multinomial mix-

ture in each class to see how it compares to mixtures learnt without such supervision.

The Traveller dataset contains 8, 000 sentence pairs, with 2, 000 pairs per class. The

size of the vocabulary and the number of singletons reﬂect the relative simplicity of this

corpus. Some statistics are shown in Table 1.

The BAF corpus [16] is a compilation of bilingual ”institutional” French-English

texts ranging from debates of the Canadian parliament (Hansard), court transcripts and

UN reports to scientiﬁc, technical and literary documents. This dataset is composed of

11 documents that are organised into 4 natural genres (Institutional, Scientiﬁc, Tech-

nical and Literary) trying to be representative of the types of text that are available in

multilingual versions. Institutional and Scientiﬁc classes comprises documents from the

original pool of 11 documents, which were theme-related, but devoted to heterogeneous

purposes or written by different authors. This fact provides the multimodal nature to the

BAF corpus that can be adequately modelled by mixture models. The BAF corpus was

aligned at the sentence level by human experts and it was initially thought to be used as

a reference corpus to evaluate automatic alignment techniques in machine translation.

Prior to performing the experiments, the BAF corpus was simpliﬁed in order to re-

duce the size of the vocabulary and discard spurious sentence pairs. This preprocessing

mainly consisted in three basic actions: downcasing, replacement of those words con-

taining a sequence of numbers by a generic label, and isolation of punctuation marks.

This basic procedure halved the size of the vocabulary and signiﬁcantly simpliﬁed this

corpus. Neither stopword lists, nor stemming techniques were applied since, as shown

in [8], it is unclear whether this further preprocessing may be convenient. As it can be

seen in Table 1, this corpus is more complex than the Traveller dataset.

Table 1. Traveller and BAF corpora statistics.

Traveller BAF

Sp En Fr En

sentence pairs 8000 18509

average length 9 8 28 23

vocabulary size 679 503 20296 15325

singletons 95 106 8084 5281

running words 86K 80K 522K 441K

5.2 Experimental Results

Several experiments were carried out to analyse the behaviour of each individual clas-

siﬁer in terms of log-likelihood and classiﬁcation error rate as a function of the number

of mixture components per class (I ∈ {1, 2, 5, 10, 20, 50, 100}). This was done for a

training and test sets resulting from a random dataset partition (1/2-1/2 split for Trav-

eller and 4/5-1/5 for BAF).

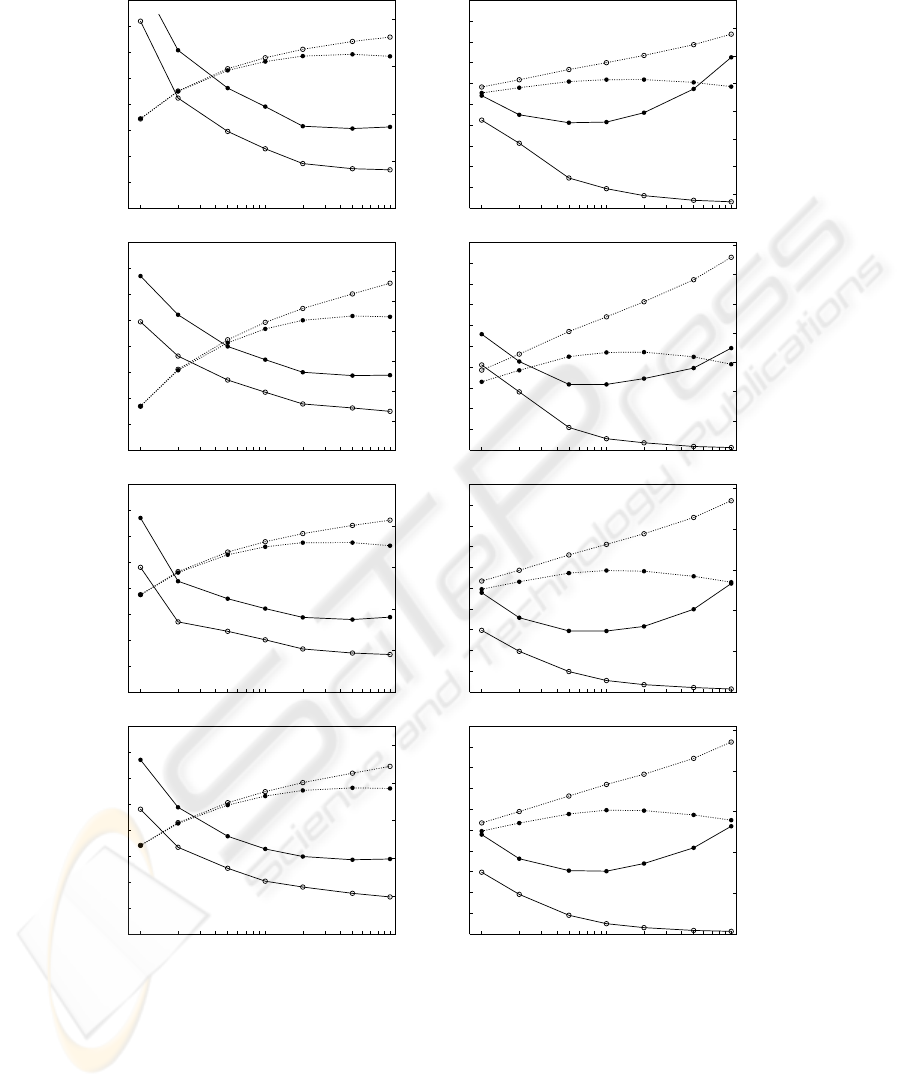
Figure 1 shows the evolution of the error rate (left y axis) and log-likelihood (right

y axis), on training and test sets, for an increasing number of mixture components (x

axis). From top to bottom rows we have: the best monolingual classiﬁer (English in

both datasets), the bilingual bag-of-words classiﬁer, and global and local classiﬁers.

Each plotted point is an average over values obtained from 30 randomised trials.

From the results in Figure 1, we can see that the evolution of the log-likelihood on

the training and test sets is as theoretically expected, for all classiﬁers in both, Traveller

and BAF. The log-likelihood in training always increases, while the log-likelihood in

test increases up to a moderate number of components (20 − 50 in Traveller and 5 −

10 in BAF). This number of components can be considered as an indication of the

number of “natural” subclasses in the data. About this number of mixture components

is also commonly found the lowest classiﬁcation test error rate, as it occurs in our case.

As the number of components keeps increasing, the well-known overtraining effect

appears, the log-likelihood in test falls and the accuracy degrades. For this reason we

decided to limit the number of mixture components to 100, since additional trials with

an increasing number of mixture components conﬁrmed this performance degradation.

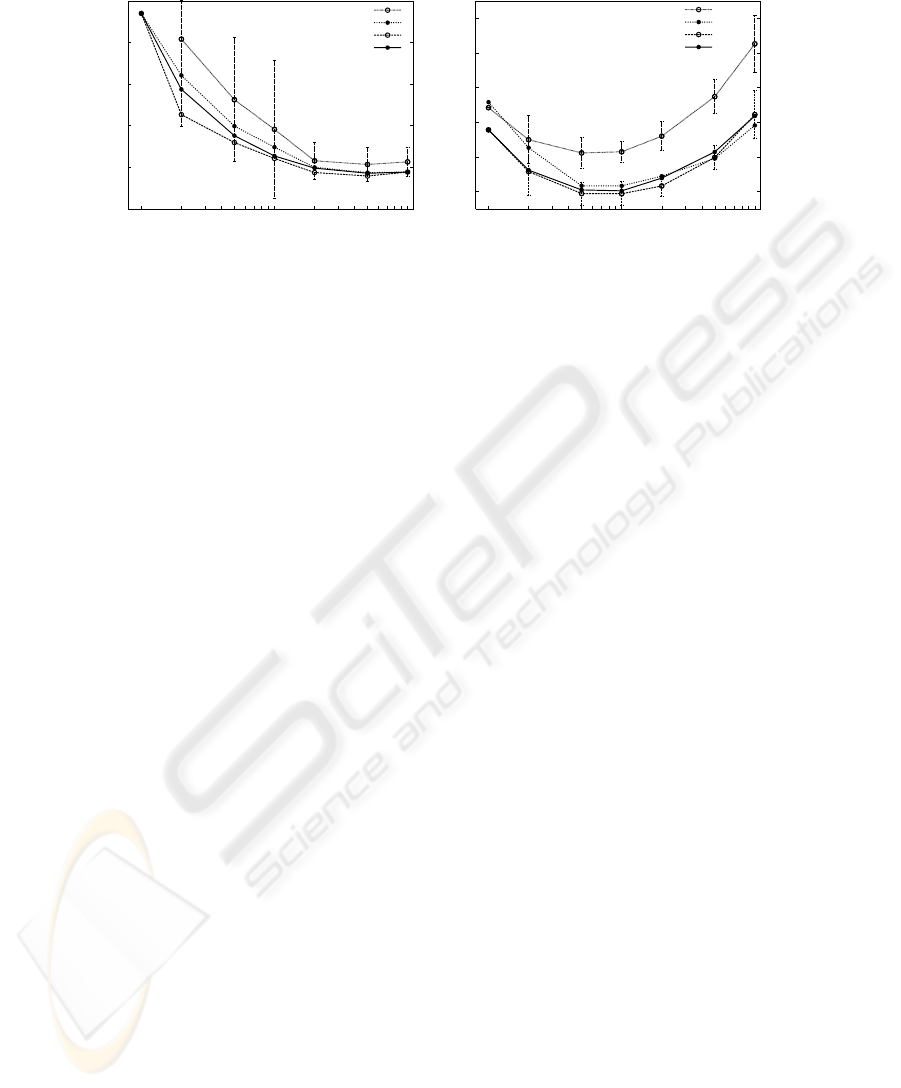
Figure 2 shows competing curves for test error-rate as a function of the number of

mixture components for the English-based, bilingual bag-of-words-based, global and

local classiﬁers; there are two plots, one for Traveller and the other for BAF. Error bars

representing 95% conﬁdence intervals are plotted for the English-based classiﬁers in

both plots, and the global classiﬁer in BAF.

From the results for Traveller in Figure 2, we can see that there is no signiﬁcant

statistical difference in terms of error rate between the best monolingual classiﬁer and

the bilingual classiﬁers. The reason behind these similar results can be better explained

in the light of the statistics of the Traveller dataset shown in Table 1. The simplicity of

the Traveller dataset, characterised by its small vocabulary size and its large number of

running words, allows for a reliable estimation of model parameters in both languages.

This is reﬂected in the high accuracy (∼ 95%) of the monolingual classiﬁers and the

little contribution of a second language to boost the performance of bilingual classiﬁers.

Nevertheless, bilingual classiﬁers seem to achieve systematically better results.

In contrast to the results obtained for Traveller, the results for BAF in Figure 2 in-

dicate that bilingual classiﬁers perform signiﬁcantly better than monolingual models.

More precisely, if we compare the curves for the English-based classiﬁer and the global

classiﬁer, we can observe that there is no overlapping between their error-rate conﬁ-

dence intervals. Clearly, the complexity and data scarcity problem of the BAF corpus

lead to poorly estimated models, favouring bilingual classiﬁers that take advantage of

both languages. However, the different bilingual classiﬁers have similar performance.

Additional experiments using smooth n-gram language models were performed

with the well-known and publicly available SRILM toolkit [17]. A Witten-Bell [18]

smoothed n-gram language model was trained for each supervised class separately and

for both languages independently. These class-dependent language models were used to

deﬁne monolingual and bilingual Naive Bayes classiﬁers. Results are given in Table 2.

From the results in Table 2, we can see that 1-gram language models are similar

to our 1-component mixture models. In fact, both models are equivalent except for the

parameter smoothing. The results obtained with n-gram classiﬁers with n > 1 are much

better that the results for n = 1 and slightly better than the best results obtained with

general I-component multinomial mixtures. More precisely, the best results achieved

with n-grams are 1.1% in Traveller and 2.6% in BAF, while the best results obtained

with multinomial mixtures are 1.4% in Traveller and 2.9% in BAF.

Table 2. Test-set error rates for monolingual and bilingual naive classiﬁers based on smooth

n-gram language models in Traveller and BAF.

Traveller 1-gram 2-gram 3-gram

English classiﬁer 4.1 1.9 1.3

Spanish classiﬁer 2.8 1.2 1.2

Bilingual classiﬁer 3.3 1.2 1.1

BAF 1-gram 2-gram 3-gram

English classiﬁer 5.3 3.5 3.6

French classiﬁer 6.7 4.4 4.4

Bilingual classiﬁer 4.1 2.8 2.6

100

0.0

0.5

1.0

1.5

2.0

2.5

3.0

3.5

4.0

1 2 5 10 20 50 100

-50

-45

-40

-35

-30

Error (%) Log-Likelihood

Mixture components

Training

Log-L

Test

Log-L

Test

Error

Training

Error

Traveller dataset

English-based classifier

100502010521

-190

-180

-170

-160

-150

-140

-130

-120

Error (%) Log-Likelihood

Mixture components

Test

Error

Training

Log-L

Training

Error

Test

Log-L

BAF dataset

English-based classifier

0.0

0.5

1.0

1.5

2.0

2.5

3.0

3.5

4.0

1 2 5 10 20 50 100

-95

-90

-85

-80

-75

-70

Error (%) Log-Likelihood

Mixture components

Training

Log-L

Test

Log-L

Test

Error

Training

Error

Traveller dataset

BBoW-based classifier

1 2 5 10 20 50 100

-380

-370

-360

-350

-340

-330

-320

-310

Error (%) Log-Likelihood

Mixture components

Test

Error

Training

Log-L

Training

Error

Test

Log-L

BAF dataset

BBoW-based classifier

0.0

0.5

1.0

1.5

2.0

2.5

3.0

3.5

4.0

1 2 5 10 20 50 100

-95

-85

-75

-65

-55

Error (%) Log-Likelihood

Mixture components

Test

Error

Training

Log-L

Training

Error

Test

Log-L

Traveller dataset

Global classifier

1 2 5 10 20 50 100

-380

-360

-340

-320

-300

-280

Error (%) Log-Likelihood

Mixture components

Test

Error

Training

Log-L

Training

Error

Test

Log-L

BAF dataset

Global classifier

0.0

0.5

1.0

1.5

2.0

2.5

3.0

3.5

4.0

1 2 5 10 20 50 100

-95

-85

-75

-65

-55

Error (%) Log-Likelihood

Mixture components

Test

Error

Training

Log-L

Training

Error

Test

Log-L

Traveller dataset

Local classifier

1 2 5 10 20 50 100

-380

-360

-340

-320

-300

-280

Error (%) Log-Likelihood

Mixture components

Test

Error

Training

Log-L

Training

Error

Test

Log-L

BAF dataset

Local classifier

Fig.1. Error rate and log-likelihood curves in training and test sets as a function of the number

of mixture components, in Traveller (left column) and BAF (right column) for the four classiﬁers

considered. Classiﬁers: the best monolingual, the bilingual bag-of-words (BBoW), the global and

the local classiﬁer.

101

1.0

1.5

2.0

2.5

3.0

3.5

1 2 5 10 20 50 100

Error (%)

Mixture components

Traveller dataset

English-based classifier

Bilingual-BoW-based classifier

Global classifier

Local classifier

3.0

4.0

5.0

6.0

7.0

8.0

1 2 5 10 20 50 100

Error (%)

Mixture components

BAF dataset

English-based classifier

Bilingual-BoW-based classifier

Global classifier

Local classifier

Fig.2. Test-set error rate curves as a function of the number of mixture components, for each

classiﬁer in Traveller (left) and BAF (right).

6 Conclusions and Future Work

We have presented three different extensions of the multinomial mixture-based text

classiﬁcation model for bilingual text: the bilingual bag-of-words model and the global

and local decomposition models. The performance of these extensions was compared

to that of monolingual and smooth n-gram classiﬁers. Two outstanding conclusions

can be stated from the results presented. First, mixture-based classiﬁers surpass single-

component classiﬁers in all cases (monolingual, bilingual bag-of-words, global and

local). In fact, we have taken advantage of the ﬂexibility of the mixture modelisa-

tion over the ”single-component” approach to further improve the error rates achieved.

This mixture modelling superiority is also reﬂected in the monolingual versions of our

text classiﬁers and corroborated through smooth n-gram language model experiments

with independent software. Second, bilingual classiﬁers outperform their monolingual

and smooth 1-gram counterparts, and the excellence of bilingual classiﬁers is more

clearly shown when the complexity of the dataset does not allow for monolingual well-

estimated models, as in the BAF corpus. Therefore, the contribution of an extra source

of information instantiated as a second language cannot be neglected.

As a future work, smooth n-gram language models for bilingual text classiﬁca-

tion provide an interesting starting point for future research based on more versatile

language models, as mixtures of bilingual n-gram language models. A promising ex-

tension of this work would be the development of mixture of 2-gram language models.

All in all, the bilingual approaches described in this work are relatively simple mod-

els for the statistical distribution of bilingual texts. More sophisticated models, such as

IBM statistical translation models [19], may be better in describing the statistical dis-

tribution of bilingual, correlated texts.

102

References

1. Jain, A.K., et al.: Statistical Pattern Recognition: A Review. IEEE Trans. on PAMI 22 (2000)

4–37

2. Sebastiani, F.: Machine learning in automated text categorisation. ACM Comp. Surveys 34

(2002) 1–47

3. Lewis, D.D.: Naive Bayes at Forty: The Independence Assumption in Information Retrieval.

In: Proc. of ECML’98. (1998) 4–15

4. McCallum, A., Nigam, K.: A Comparison of Event Models for Naive Bayes Text Classiﬁ-

cation. In: AAAI/ICML-98 Workshop on Learning for Text Categorization. (1998) 41–48

5. Juan, A., Vidal, E.: On the use of Bernoulli mixture models for text classiﬁcation. Pattern

Recognition 35 (2002) 2705–2710

6. Nigam, K., et al.: Text Classiﬁcation from Labeled and Unlabeled Documents using EM.

Machine Learning 39 (2000) 103–134

7. Novovicov

a, J., Mal

ık, A.: Application of Multinomial Mixture Model to Text Classiﬁcation.

In: Proc. of IbPRIA 2003. (2003) 646–653

8. Vilar, D., et al.: Effect of Feature Smoothing Methods in Text Classiﬁcation Tasks. In: Proc.

of PRIS’04. (2004) 108–117

9. Pavlov, D., et al.: Document Preprocessing For Naive Bayes Classiﬁcation and Clustering

with Mixture of Multinomials. In: Proc. of KDD’04. (2004) 829–834

10. Peng, F., et al.: Augmenting Naive Bayes classiﬁers with statistical language models. Infor-

mation Retrieval 7 (2003) 317–345

11. Rennie, J., et al.: Tackling the Poor Assumptions of Naive Bayes Text Classiﬁers. In: Proc.

of ICML’03. (2003) 616–623

12. Scheffer, T., Wrobel, S.: Text Classiﬁcation Beyond the Bag-of-Words Representation. In:

Proc. of ICML’02 Workshop on Text Learning. (2002)

13. Cubel, E., et al.: Adapting ﬁnite-state translation to the TransType2 project. In: Proc. of

EAMT/CLAW’03, Dublin (Ireland) (2003) 54–60

14. Dempster, A.P., et al.: Maximum likelihood from incomplete data via the EM algorithm

(with discussion). Journal of the Royal Statistical Society B 39 (1977) 1–38

15. Vidal, E., et al.: Example-Based Understanding and Translation Systems. Report ESPRIT

project (2000)

16. Simard, M.: The BAF: A Corpus of English-French Bitext. In: Proc. of LREC’98. (1998)

489–496

17. Stolcke, A.: SRILM – an extensible language modeling toolkit. In: Proc. of ICSLP’02.

Volume 2. (2002) 901–904

18. Witten, I.H., et al.: The zero-frequency problem: Estimating the probabilities of novel events

in adaptive text compression. IEEE Trans. on Information Theory 37 (1991) 1085–1094

19. Brown, P.F., et al.: A Statistical Approach to Machine Translation. Comp. Linguistics 16

(1990) 79–85

103