The Way of Adjusting Parameters of the Expert
System Shell McESE: New Approach
I. Bruha
1
and F. Franek
1
1
McMaster University, Department of Computing & Software
Hamilton, Ont., Canada, L8S4K1
Abstract. We have designed and developed a general knowledge representation
tool, an expert system shell called McESE (McMaster Expert System Environ-
ment); it derives a set of production (decision) rules of a very general form.
Such a production set can be equivalently symbolized as a decision tree.
McESE exhibits several parameters such as the weights, thresholds, and the
certainty propagation functions that have to be adjusted (designed) according to
a given problem, for instance, by a given set of training examples. We can use
the traditional machine learning (ML) or data mining (DM) algorithms for in-
ducing the above parameters can be utilized.
In this methodological case study, we discuss an application of genetic algo-
rithms (GAs) to adjust (generate) parameters of the given tree that can be then
used in the rule-based expert system shell McESE. The only requirement is that
a set of McESE decision rules (or more precisely, the topology of a decision
tree) be given.
1 Introduction
When developing a decision-making system, we (as builders, knowledge engineers)
utilize an existing expert system shell, either developed by ourselves or by a
specialized expert-system tool builder.
We have designed and implemented a software tool (expert system shell) called
McESE (McMaster Expert System Environment) that yields (induces) a set of
production (decision) rules of a very general form; among all, one of its advantages is
a large set of several routines for handling uncertainty [9], [10].
Note that a production (decision) set derived by the system McESE can be
equivalently exhibited as a decision tree. The main and only constraint of our new
approach is that we expect in this methodological case study that the logical structure
(topology) of a set of decision rules (a decision tree) is given. The point of this study
consists in that even if this logical structure is provided, particularly in real-world
tasks, the designer may be faced with the lack of knowledge of other parameters of
the tree. These parameters are usually adjustable values (either discrete or numerical
ones) of production rules or other knowledge representation formalisms such as
frames.
Bruha I. and Franek F. (2006).
The Way of Adjusting Parameters of the Expert System Shell McESE: New Approach.
In 6th International Workshop on Pattern Recognition in Information Systems, pages 119-126
DOI: 10.5220/0002470301190126
Copyright
c
 SciTePress

Our McESE system exhibits these parameters: the weights and thresholds for
terms and the selection of the certainty value propagation functions (CVPF for short)
from a predefined set. In order to select the optimal (or at least suboptimal)
values/formulas for these parameters we use the traditional approach of machine
learning (ML) and data mining (DM); we adjust the above parameters according to a
set of training (representative) observations (examples). However, we use a different
and relatively new approach for the inductive process based on the paradigm of
genetic algorithms (GAs).
A genetic algorithm includes a long process of evolution of a large population of
chromosomes (individuals, objects) before selecting optimal values that have a better
chance of being globally optimal compared to the traditional methods. The funda-
mental idea is simple: individuals (chromosomes) selected according to a certain
evaluation criterion are allowed to crossover so as to produce one or more offsprings.
The offsprings are slightly different from their ‘parents’. Any generic algorithm
evidently performs according to how the term ‘slightly different’ and evaluation
criterion are defined.
We present in this paper a simulation of applying GAs to generate/adjust the
parameter values of a McESE decision tree. Section 2 briefly describes our rule-based
expert system shell McESE with emphasis on the form of rules. Section 3 then
surveys the structure of GAs. Afterwards, Section 4 introduces the methodology of
this project including a case study.
2 Methodology: Rule-based Expert System Shell McESE
McESE (McMaster Expert System Environment) [9], [10] is an interactive
environment for design, creation, and execution of backward as well as forward
chaining rule-based expert systems. The main objectives of the project are focused on
two aspects: (i) to provide extensions of regular languages to deal with McESE rule
bases and inference with them, and (ii) a versatile machinery to deal with uncertainty.
As for the first aspect, the language extension is facilitated through a set of
functions with the native syntax that provide the full functionality required (for
instance, in the Common-Lisp extension these are Common-Lisp functions callable
both in the interactive or compiled mode, in the C extension, these are C functions
callable in any C program).
As for the latter one, the versatility of the treatment of uncertainty is facilitated by
the design of McESE rules utilizing weights, threshold directives, and CVPF's
(Certainty Value Propagation Function). The McESE rule has the following syntax:
R: T
1
& T
2
& .... & T
n
=F=> T
T
1
,...,T
n
are the left-hand side terms of the rule R and T is the right-hand side term of
the rule R, F symbolizes a formula for the CVPF.
A term has the form:
weight * predicate [op cvalue]
where weight is an explicit certainty value,
predicate is a predicate possibly with variables (it could be negated by ~ ), and
120

op cvalue is the threshold directive: op can either be >, >=, <, or <=, and cvalue is
an explicit certainty value.
If the weight is omitted it is assumed to be 1 by default. The threshold directive can
also be omitted. The certainty values are reals in the range 0..1 .
It should be emphasized that a value of a term depends on the current value of the
predicate for the particular instantiation of its variables; if the threshold directive is
used, the value becomes 0 (if the current value of the predicate does not satisfy the
directive), or 1 (if it does). The resulting value of the term is then the value of the
predicate modified by the threshold directive and multiplied by the weight.
When the backward-chaining mode is used in the McESE system, each rule that
has the predicate being evaluated as its right-hand side predicate is eligible to ‘fire’.
The firing of a McESE rule consists of instantiating the variables of the left-hand side
predicates by the instances of the variables of the right-hand size predicate, evaluating
all the left-hand side terms and assigning the new certainty value to the predicate of
the right-hand side term (for the given instantiation of variables). The value is com-
puted by the CVPF F based on the values of the terms T
1
,...,T
n
. In simplified terms,
the certainty of the evaluation of the left-hand side terms determines the certainty of
the right-hand side predicate. There are several built-in CVPF’s the user can use (min,
max, average, weighted average), or the user can provide his/her own custom-made
CVPF's. This approach allows, for instance, to create expert systems with fuzzy logic,
or Bayesian logic, or many others [14].
It is a widely known conflict that any rule-based expert system must deal with the
problem of which of the eligible rules should be ‘fired’. This is dealt with by what is
commonly referred to as conflict resolution. This problem in McESE is slightly
different; each rule is fired and it provides an evaluation of the right-hand predicate –
and we face the problem which of the evaluation should be used. McESE provides the
user with three predefined conflict resolution strategies: min (where one of the rules
leading to the minimal certainty value is considered fired), max (where one of the
rules leading to the maximal certainty value is considered fired), and rand (a
randomly chosen rule is considered fired). The user has the option to use his/her own
conflict resolution strategy as well.
3 Survey of Genetic Algorithms
Data Mining (DM) consists of several procedures that process the real-world data.
One of its components is the induction of concepts from databases; it consists of
searching usually a large space of possible concept descriptions. There exist several
paradigms how to control this search, for instance various statistical methods, logi-
cal/symbolic algorithms, neural nets, and the like. However, such traditional
algorithms select immediate (usually local) optimal values.
The genetic algorithms (GAs) exhibit a newer paradigm for search of concept
descriptions. They comprise a long process of evolution of a large population of
individuals (objects, chromosomes) before selecting optimal values, thus giving a
‘chance’ to weaker, worse objects. They exhibit two important characteristics: the
search is usually global and parallel in nature since a GA processes not just a single
individual but a large set (population) of individuals.
121

Genetic algorithms utilize (emulate) biological evolution and are generally
utilized in optimization processes. The optimization is performed by processing a
population of individuals (chromosomes). A designer of a GA has to provide an
evaluation function, called fitness, that evaluates any individual. The fitter individual
is given a greater chance to participate in forming of the new generation. Given an
initial population of individuals, a genetic algorithm proceeds by choosing individuals
to become parents and then replacing members of the current population by the new
individuals (offsprings) that are modified copies of their parents. This process of
reproduction and population replacement continues until a specified stop condition is
satisfied or the predefined amount of time is exhausted.
Genetic algorithms exploit several so-called genetic operators:
• Selection operator chooses individuals (chromosomes) as parents depending on
their fitness; the fitter individuals have on average more children (offsprings)
than the less fit ones. Selecting the fittest individuals tends to improve the popu-
lation.
• Crossover operator creates offsprings by combining the information involved in
the parents.
• Mutation causes the offsprings to differ from their parents by introducing a
localized change.
• Optional are other routines such as high-claiming that processes (modifies)
the objects in a narrow ‘neighbourhood’ of each new offspring.
Details of the theory of genetic algorithms may be found in several books, e.g. [11],
[13]. There are many papers and projects concerning genetic algorithms and their
incorporation into data mining [1], [8], [4], [5], [12], [15], [16].
We now briefly describe the performance of the genetic algorithm we have
designed and implemented for general purposes, including this project. The
foundation for our algorithms is the CN4 learning algorithm [2], a significant
extension of the well-known algorithm CN2 [6], [7]. For our new learning algorithm
(genetic learner) GA-CN4, we removed the original search section (so-called beam
search) from the inductive algorithm and replaced it by a domain-independent genetic
algorithm working with fixed-length chromosomes. The other portion of the original
CN4 remain unchanged; its parameters have been set to their default values.
The learning starts with an initial population of individuals (chromosomes) and
lets them evolve by combining them by means of genetic operators introduced above.
More precisely, its high-level logic can be described as follows:
procedure GA
Initialize randomly a new population
Until stop condition is satisfied do
1. Select individuals by the tournament selection operator
2. Generate offsprings by the two-point crossover operator
3. Perform the bit mutation
4. Check whether each new individual has the correct value (depending
on the type of the task); if not the individual's fitness is set to 0 (i.e., to
the worst value)
enddo
Select the fittest individual
122

If this individual is statistically significant then
return it
else return nil
The above algorithm mentions some particular operations used in our GA. Their
detailed description can be found e.g. in [3], [11], [13]. More specifically:
- the generation mode of replacing a population is used;
- the fitness function is derived from the Laplacian evaluation formula.
The default parameter values in our genetic algorithm: size of population is 30,
probability of mutation Pmut = 0.002 . The genetic algorithm stops the search when
the Laplacian criterion does not improve after 10000 generations.
Our GA also includes a check for statistical significance of the fittest individual. It
has to comply with the statistical characteristics of a database which is used for
training; the χ
2
-statistics is used for this test of conformity. If no fittest individual can
be found, or it does not comply with the χ
2
-statistic, then nil is returned in order to
stop further search; the details can be found in [4].
4 A Case Study
As we have already stated our methodological study utilizes GA-CN4 for deriving
some parameters of the rule-based expert system McESE. Particularly, an individual
(chromosome) is formed by a fixed-length list (array) of the following parameters of
the McESE system:
- the weight of each term of McESE rule,
- the threshold value cvalue of each term,
- the selection of the CVPF of each rule from a predefined set of CVPF’s
- the conflict resolution for the entire decision tree.
Note that our GA-CN4 is able to process numerical (continuous) attributes;
therefore, the above parameters weight and cvalue can be properly handled. As for the
CVPF, it is considered as a discrete attribute with these singular values (as mentioned
above): min, max, average, and weighed average. Similarly, the conflict resolution is
treated as a discrete attribute.
Since the list of the above parameters is of the fixed size, we can apply the GA-
CN4 algorithm that can process the fixed-length chromosomes (objects) only.
The entire process of deriving the right values of the above parameters (weights,
cvalues, CVPF’s, conflict resolution) looks as follows:
1. A dataset of typical (representative) examples for a given task is selected
(usually by a knowledge engineer that is to solve a given task).
2. The knowledge engineer (together with a domain expert) induces the set of
decision rules, i.e. the topology of the decision tree, without specifying values of
the above parameters.
3. The genetic learner GA-CN4 induces the right values of the above parameters by
processing the training database.
123

To illustrate our new methodology of knowledge acquisition we introduce the
following case study. We consider a very simple task of heating and mixing three
liquids L
1
, L
2
, and L
3
. The first two have to be controlled by their flow and
temperature; then they are mixed with L
3
. Thus, we can derive these four rules:
R
1
: w
11
* F
1
[>= c
11
] & w
12
* T
1
[>= c
12
] =f
1
=> H
1
R
2
: w
21
* F
2
[>= c
21
] & w
22
* T
2
[>= c
22
] =f
2
=> H
2
R
3
: w
31
* H
1
[>= c
31
] & w
32
* F
1
[>= c
32
] &
w
33
* H
2
[>= c
33
] & w
34
* F
3
[>= c
34
] =f
3
=> A
1
R
4
: w
41
* H
2
[>= c
41
] & w
42
* F
2
[>= c
42
] &
w
43
* H
1
[>= c
43
] & w
44
* F
3
[>= c
44
] =f
4
=> A
2
Here F
i
is the flow of L
i
, T
i
its temperature, H
i
the resulting mix, A
i
the adjusted mix,
i =1, 2 (or 3). The corresponding decision tree is on Fig. 1.
We assume that the above topology of the decision tree (without the right values
of its parameters) was derived by the knowledge engineer. The unknown parameters
w
ij
, c
ij
, f
i
, including the conflict resolution then form a chromosome (individual) of
length 29 attributes. The global optimal value of this chromosome is then induced by
the genetic algorithm GA-CN4.
5 Analysis
This project was to design a new methodology for inducing parameters for an expect
system under the condition that the topology (the decision tree) is known. We have
selected domain-independent genetic algorithm that searches for a global optimizing
parameters values.
Our analysis of the methodology indicates that it is quite a viable one. The
traditional algorithms explore a small number of hypotheses at a time, whereas the
genetic algorithm carries out a parallel search within a robust population. The only
disadvantage our study found concerns the time complexity. Our genetic learner is
about 20 times slower than the traditional machine learning algorithms. This disad-
vantage can be overcome by a specialized hardware of parallel processors; however,
this can be accomplished at a highly distinguished research units.
In the near future, we are going to implement the entire system discussed here and
compare it with other inductive data mining tools. The McESE system will thus
comprise another tool for rule-base knowledge processing (besides neural net and
Petri nets) [10].
The algorithm GA-CN4 is written in C and runs under both Unix and Windows.
The McESE system has been implemented both in C and Lisp.
References
1. Bala, J. et al.: Hybrid learning using genetic algorithms and decision trees for pattern
classification. Proc. IJCAI-95 (1995), 719-724
124

2. Bruha, I. and Kockova, S.: A support for decision making: Cost-sensitive learning system.
Artificial Intelligence in Medicine, 6 (1994), 67-82
3. Bruha, I., Kralik, P., Berka, P.: Genetic learner: Discretization and fuzzification of
numerical attributes. Intelligent Data Analysis J., 4 (2000), 445-460
4. Bruha, I.: Some enhancements in genetic learning: A case study on initial population. 14th
International Symposium on Methodologies for Intelligent Systems (ISMIS-2003), Japan
(2003), 539-543
5. Bruha, I.: Rule representation and initial population in genetic learning. Industrial
Simulation Conference: Complex System Modelling (ISC-2005), Berlin (2005), 37-41
6. Clark, P. and Boswell, R.: Rule induction with CN2: Some recent improvements. EWSL-
91, Porto, Springer-Verlag (1991), 151-163
7. Clark, P. and Niblett, T.: The CN2 induction algorithm. Machine Learning, 3 (1989), 261-
283
8. De Jong, K.A., Spears, W.M., Gordon, D.F.: Using genetic algorithms for concept learning.
Machine Learning, 13, Kluwer Academic Publ., 161-188
9. Franek, F.: McESE-FranzLISP: McMaster Expert System Extension of FranzLisp. In:
Computing and Information, North-Holland (1989)
10. Franek, F. and Bruha, I.: An environment for extending conventional programming
languages to build expert system applications. Proc. IASTED Conf. Expert Systems,
Zurich (1989)
11. Goldberg, D.E.: Genetic algorithms in search, optimization, and machine learning.
Addison-Wesley (1989)
12. Giordana, A. and Saitta, L.: REGAL: An integrated system for learning relations using
genetic algorithms. Proc. 2nd International Workshop Multistrategy Learning (1993), 234-
249
13. Holland, J.: Adaptation in natural and artificial systems. University Michigan Press, Ann
Arbor (1975)
14. Jaffer, Z.: Different treatments of uncertainty in McESE. MSc. Thesis, Dept Computer
Science & Systems, McMaster University (1990)
15. Janikow, C.Z.: A knowledge-intensive genetic algorithm for supervised learning. Machine
Learning, 5, Kluwer Academic Publ. (1993), 189-228
16. Turney, P.D.: Cost-sensitive classification: Empirical evaluation of a hybrid genetic
decision tree induction algorithm. J. Artificial Intelligence Research (1995)
125

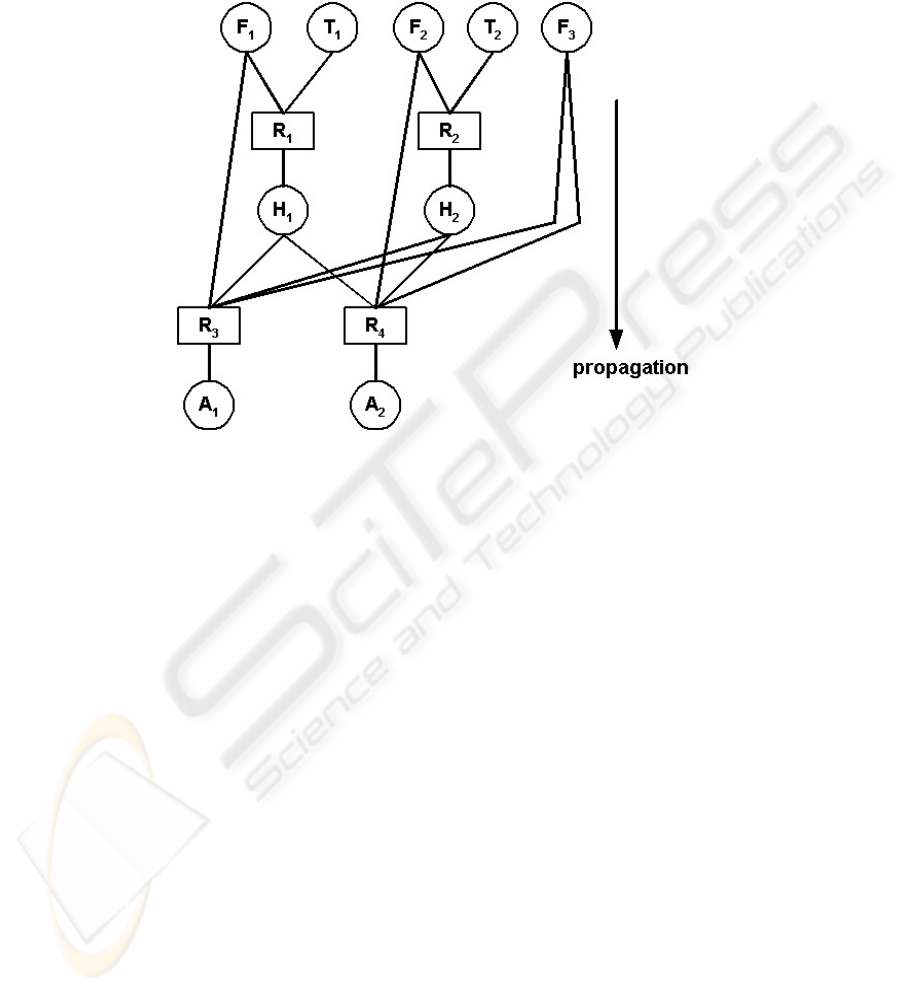
Fig. 1. The decision tree of our case study.
126