
FACE RECOGNITION FROM SKETCHES USING ADVANCED
CORRELATION FILTERS USING HYBRID EIGENANALYSIS
FOR FACE SYNTHESIS
Yung-hui Li
Language Technology Institute, Carnegie Mellon Universty
Marios Savvides and Vijayakumar Bhagavatula
Department of Electrical and Computer Engineering, Carnegie Mellon University
Keywords: Face from sketch synthesis, face recognition, eigenface, advanced correlation filters, OTSDF.
Abstract: Most face recognition systems focus on photo-based (or video) face recognition, but there are many
law-enforcement applications where a police sketch artist composes a face sketch of the criminal and that is
used by the officers to look for the criminal. Currently state-of-the-art research approach transforms all test
face images into sketches then perform recognition in the sketch domain using the sketch composite,
however there is one flaw in such approach which hinders it from being deployed fully automatic in the
field, due to the fact that generating a sketch image from a surveillance footage will vary greatly due to
illumination variations of the face in the footage under different lighting conditions. This will result
imprecise sketches for real time recognition. In our approach we propose the opposite which is a better
approach; we propose to generate a realistic face image from the composite sketch using a Hybrid subspace
method and then build an illumination tolerant correlation filter which can recognize the person under
different illumination variations. We show experimental results on our approach on the CMU PIE (Pose
Illumination and Expression) database on the effectiveness of our novel approach.
1 INTRODUCTION
Face recognition has attracted much attention in
recent years and many different methods have been
proposed (Zhao, 2000). However, most of the
proposed methods focus on the problem where both
training and testing images are face images. In
practical law-enforcement scenarios, we may
encounter the situation where a police-sketch of a
suspects face image is available. For example, in
many criminal investigations there are usually one or
two human witnesses that have caught a glimpse of
the criminal or terrorist suspects and the police and
government authorities must use this vital
information as a means to catch these suspects. In
such cases, typically a professional police sketch
artist will work and co-operate with the witnesses to
develop and synthesize a police sketch of the suspect.
This sketch is then distributed among police officers
in efforts to look for the suspects at ports of entry or
other locations.
Figure 1: Examples of face and their sketch images.
In this case, we only have the drawing or sketch
image of the subject to work with. In this paper we
propose a novel approach of trying to retrieve or
synthesize a real face image that can be used by
law-enforcement personnel and more importantly by
an automatic face recognition system.
11
Li Y., Savvides M. and Bhagavatula V. (2006).
FACE RECOGNITION FROM SKETCHES USING ADVANCED CORRELATION FILTERS USING HYBRID EIGENANALYSIS FOR FACE SYNTHESIS.
In Proceedings of the Eighth International Conference on Enterprise Information Systems - HCI, pages 11-18
DOI: 10.5220/0002457400110018
Copyright
c
SciTePress
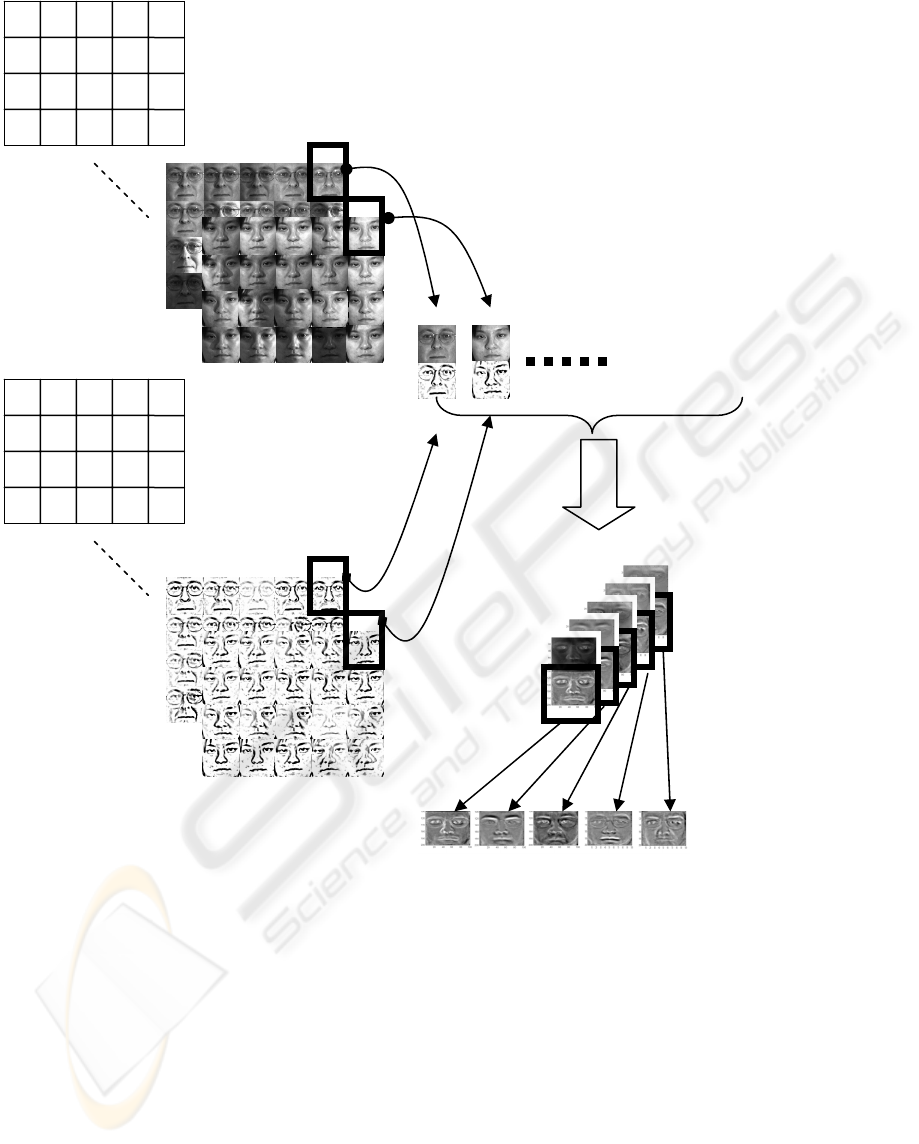
Figure 1 shows a couple of examples of face
images and their corresponding sketch images. One
can easily observe that face and sketch have
different modalities. In general, sketch images are
more focused on the prominent shape parts of face
(eyes, nose, mouth). In short, information in sketch
images is much fewer than information in face
images. Therefore, performing recognition based on
sketch images is harder than doing it on face images.
1.1 Previous Work
Wang & Tang (Tang, 2002, 2003, 2004, 2005) have
tackled this approach in a different way. They divide
the task into two phases: At the first phase, they
transform all the face images in their database into
sketch images using various approaches, for
example, eigenspace (Tang, 2004) and LLE (Tang,
2005). This phase can be called “synthesis phase”.
Second, they perform all the recognition tasks on
sketch image domain using a different approach, for
(Hybrid Space)
Hybrid
Eigenvectors
Pseudo-eigensketch is the lower half of the hybrid
eigenvectors
Face images
Sketch images
Figure 2: Illustration of experimental procedure during training phase.
ICEIS 2006 - HUMAN-COMPUTER INTERACTION
12

example, distance metric (Tang, 2004), Bayesian,
LDA, PCA and KNDA (Tang, 2005).
2 PROPOSED METHOD
Due to the observation that information is fewer in
sketch space, we propose a new method to attach
face-sketch recognition problem which is exactly the
opposite way to the method described in (Tang,
2002, 2003, 2004, 2005). We propose a novel
algorithm to reconstruct face image from its sketch
counterpart, and by means of a powerful pattern
recognition technique, as shown in (Savvides, 2002,
2004, 2005), we can perform recognition in face
subspace even if our database for matching only
have candidate images taken in very bad
illumination condition. More importantly, our
proposed approach can be implemented into a fully
automatic system which can be easily deployed in
real life scenario.
2.1 Training Phase
Our problem in training phase can be stated as
following: Given a database consisted of face
images from many people and corresponding sketch
images, how can we derive a set of feature that can
catch the intrinsic mapping function between face
and sketch images. How do we practically calculate
those features? How can we use those features to do
the pattern matching task when there’s a new sketch
image coming in?
The state-of-the-art technique in face recognition
gives us an implication for this problem. It has been
shown that performing eigen-analysis over face
images, as stated in (Turk, 1991), can capture the
principle components in a set of face images, and
those principle components (eigenfaces) can be very
Figure 3: The comparison of eigenfaces derived from three difference spaces. The first row is the eigenfaces derived from
hybrid space. The second row is the eigenfaces derived from face images only. The third row is the eigensketch derived
from sketch images only. Note that while the pseudo-eigenface and pseudo-eigensketch images are highly correlated
among the images at first row, the eigenfaces in second row are not correlated to the eigensketch in third row. Hence,
calculating eigenface and eigensketch independently will not keep the corresponding information between each other,
while calculating eigenface in hybrid space will
.
FACE RECOGNITION FROM SKETCHES USING ADVANCED CORRELATION FILTERS USING HYBRID
EIGENANALYSIS FOR FACE SYNTHESIS
13
helpful later when we are interested in
reconstructing new face images.
If we decide to use eigenface approach to attack
this problem, the next question is: how are we going
to utilize eigenface technique to derive features
across both face and sketch subspace? Face and
sketch images are very different, so if we perform
eigen-analysis over face and sketch subspace
independently and get eigenface and eigensketches
respectively, and substitute the projection
coefficients from one subspace to another, basically
we are assuming the transformation between face
and sketch are linear, as stated in (Tang, 2003). But
in practice, since sketch images are drawn by artists,
it is not a linear transformation, thus we propose a
solution based on performing eigen-analysis in
hybrid subspace. By hybrid subspace, we are saying
that we create a subspace by concatenating face and
sketch images. After creating data in such
face-sketch hybrid subspace, we perform
eigen-analysis on this subspace and get the
eigenvector matrix in this hybrid subspace. The
basic flow of training is described in section 3.2,
also shown in Figure 2.
Note there is an interesting fact that if we
calculate eigenface and eigensketch independently
from our database, the resulting eigenfaces are not
correlated to resulting eigensketches, as shown in
Figure 3. But by performing eigen-analysis on
hybrid subspace, we can clearly see that the upper
half of each eigenvector is highly correlated with the
lower half of it, which means our proposed method
can capture the nonlinear mapping function between
face and sketch images.
After we get eigenvector matrix in hybrid
subspace, we retrieve the eigensketch matrix by only
keeping the lower half of each eigenvector of hybrid
subspace. Note that these eigensketch vectors we get
with this method may not be orthonormal to each
other since the orthogonality has been destroyed by
cropping out the upper half of the vector. So we
will call them “pseudo-eigensketches”.
2.2 Reconstruction Phase
At testing phase, our job can be divided in two
stages: reconstruction phase and recognition phase.
At reconstruction phase, when a new sketch
image comes in, our goal is to reconstruct the
original face image corresponding to this sketch that
can be used by police officers to look for the person
and this image can also be fed into the automatic
face recognition system to look for the person in
real-time systems.
Since we already have the “pseudo-eigensketch”
computed from training phase, we follow the typical
eigenface approach to reconstruct face. First, we
compute the projection coefficients of this sketch
over pseudo-eigensketch. Since our
“pseudo-eigensketch” is not a set of orthonormal
basis, we use pseudo-inverse least squares fitting
technique to compute the projection coefficients
which produce the sketch with the least-squared
error. After we have those coefficients, we
reconstruct the facie image in hybrid subspace by
using the computed least-square projection sketch
coefficients on the pseudo-eigenfaces in hybrid
subspace.
Probe sketch
Ps
Projection
coefficient
Pseudo-eigens
ketch
Hybrid subspace
Eigenvector
Reconstructed
image in hybrid
subspace
Reconstructed face
image
Pseudo-
inverse
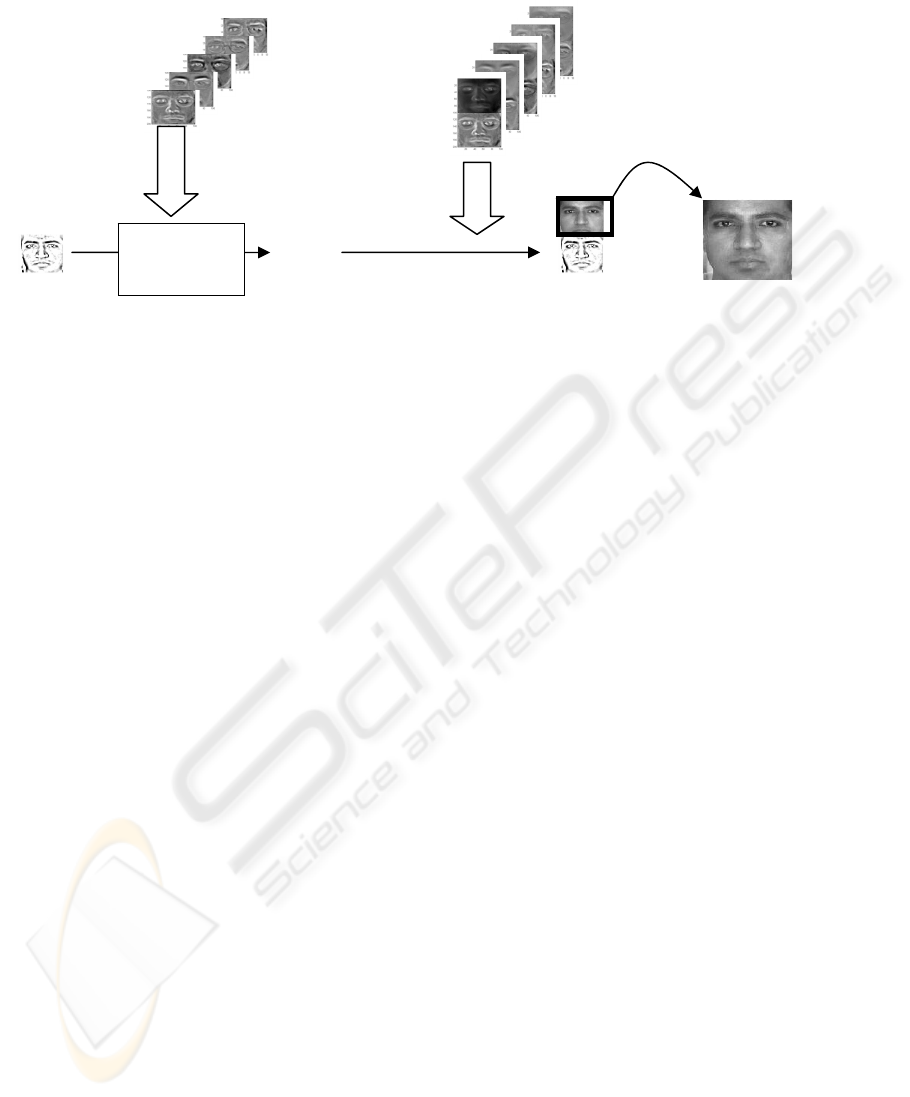
Figure 4: Illustration of experimental procedure during reconstruction phase.
ICEIS 2006 - HUMAN-COMPUTER INTERACTION
14
()
(
) ()
()
Cdevstd
CmeanC
CPCE
.
max −
=
The whole reconstruction process is illustrated in
Figure 4. Some example of pairs of original face and
reconstructed face are shown in Figure 5.
One can also notice that the reconstructed
images are a little brighter than the original ones,
this is due to some ambiguity as the sketch images
completely ignore So, if we perform recognition
with distance-based metric, like one nearest
neighbour (1NN), the distance between original
image and reconstructed ones will be very large.
Therefore, we have to use a robust pattern
recognition method which is able to handle the
illumination variation and still be able to achieve a
good recognition result. To achieve this we choose
advanced correlation filter as our recognition
approach.
2.3 Recognition Phase – Using
Advanced Correlation Filters
Advanced correlation filters (Kumar, 1992) are
advanced template-based classifiers that when
correlated with an image result in a correlation
plane. The correlation plane C measures the
correlation between the filter and the image.
Correlation of a class-specific filter with authentic
and impostor data yield very different correlation
planes. Figure 6 demonstrates this difference. These
advanced correlation filters optimize specific criteria
to obtain sharp correlation peak outputs as shown
below; this is very different from matched filters or
normalized correlation approaches which are more
common in the literature.
To quantify the difference between the two types
of correlation planes, we define a measure of
recognition called Peak to Correlation Energy
(PCE). This is a measure the sharpness of the largest
peak in the correlation output with respect to the rest
of the correlation plane.
(1)
The Minimum Average Correlation Energy
(MACE) Filter (Mahalanobis, 1987) is designed to
minimize the average energy E in the correlation
plane or Average Correlation Energy (ACE). In
the filter design h we also constrain the value of the
correlation peak at the origin to be set to 1.
Assuming that we have a matrix X which contains
the 2D Fourier transforms of training images along
the columns we can write the linear constraints as
follows:
X
+
h=u (2)
To achieve peak sharpness we must then also
minimize correlation plane energy, thus we compute
the average power spectrum of the face image which
is vectorized and placed on the diagonal of matrix D.
Our goal is to minimize E which is defined as:
DhhE
+
= (3)
where
+
denotes the conjugate transpose. The
constrained minimization of equation 2 results in the
MACE filter h
MACE.
(4)
where u is the constrained peak values (vector of
ones).
(
)
uXDXXDh
MACE
1
11
−
−+−
=
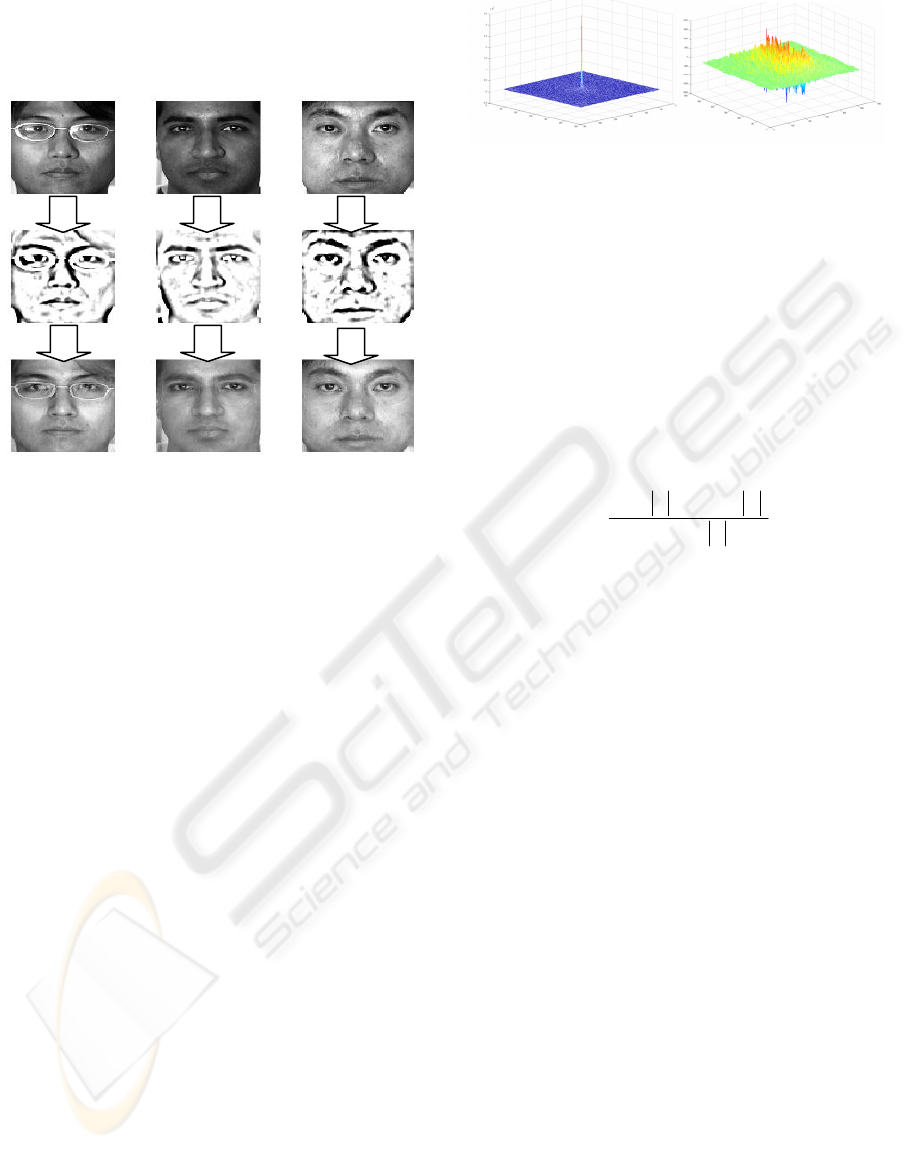
Figure 5: Examples of original face and corresponding
reconstructed face when we only have sketch images.
The images in first row are original face; the images i
n
second row are sketch of the face images, and the images
in third row are reconstructed face images from sketches.
Figure 6: Left: correlation plane of an authentic sample.
Right: Correlation plane of an imposter sample.
FACE RECOGNITION FROM SKETCHES USING ADVANCED CORRELATION FILTERS USING HYBRID
EIGENANALYSIS FOR FACE SYNTHESIS
15

The Unconstrained MACE (UMACE) Filter
(Mahalanobis, 1994) removes the constraint on the
peak value. By removing this constraint, we may be
able to find a better solution to the energy
minimization. Instead, we try to maximize the
average value of the peaks or Average Correlation
Height (ACH). The closed form solution to the
UMACE filter h
UMACE
:
h
UMACE
= D
-1
m (5)
where m is the average of the columns of X.
We will consider generalizations of the MACE
and UMACE filters called the Optimal Tradeoff
Synthetic Discriminant Function (OTSDF) filter
(Kumar, 1994) and the Unconstrained OTSDF
(UOTSDF) filter respectively. These generalized
filters offer sharp correlation peaks and some noise
tolerance. Given a desired proportion of peak
sharpness to noise tolerance, the filter designs
h
OTSDF
and h
UOTSDF
are:
(6)
(7)
where T is defined as:
(8)
where C is the assumed to be white noise power
spectral density (so in this case C=I the identity
matrix). In this paper we use OTSDF (alpha=0.99)
throughout all the recognition experiments.
3 EXPERIMENTS
The database we used in our experiment is
CMU-PIE database (Sim, 2001). The PIE database
consists two datasets which we will refer to as Light
(images captured with ambient background lighting)
and NoLight(images captured without any
background lighting on). Light database contains the
pictures which were taken under sufficient
environmental lighting, so in general one can see
clear face images in all pictures in Light database.
NoLight database contains pictures taken in the
harshest illumination conditions, so the face suffers
with larger cast shadows making face recognition in
NoLight database a much harder task than in the PIE
Light database because of these harsh illumination
variations.
There are 65 people in both databases. In Light
database, each person has 22 images; in NoLight,
each person has 21 images captured under different
lighting variations. Total number of images in this
database is 2795. CMU-PIE database has following
characteristics:
z Contains both male and female faces
z Contains people from different race and
color
z Contains images of people with and
without glasses.
z Contains severe illumination variation
across images of each person, as shown in
Figure 7 and 8.
As one can imagine, due to the large variation in
gender, skin colour, the presence or absence of
eye-glasses, and illumination; this is a very
mTh
UOTSDF
1−
=
()
uXTXXTh
OTSDF
1
11
−
−+−
=
101
2
≤≤−+=
ααα
givenCDT
Figure 7: Examples of CMU-PIE-Light database. For each person there’re 22 images, each of which has different
orientation of illumination
.
Figure 8: Examples of CMU-PIE-NoLight database. For each person there’re 21 images, each of which has different
orientation of illumination
.
ICEIS 2006 - HUMAN-COMPUTER INTERACTION
16

challenging task to perform face recognition on this
database.
Since CMU-PIE database only contains face
images and not sketch images, we have to generate
corresponding sketch images for each of the face
image in database. We used one of the non-linear
sketch functions in Adobe PhotoShop® to manually
generate all corresponding sketch images for each of
the face. Examples of face and sketch images are
shown in Figure 1.
During the training phase, we selected two
images with evenly distributed illumination (i.e.
neutral frontal lighting) from every person, calculate
eigenvectors in hybrid subspace. During recognition,
we pick one sketch image, then reconstruct the face
image using algorithm described in Section 2.1.
Then from all face images of each person, we match
the reconstructed face image with all rest images (all
images except the two for training and the one for
reconstruction). The rational for doing this is to
simulate the real scenario when our system is
applied in real life where the person we are looking
for is walking under varying illumination causing
their facial appearance to vary significantly due to
lighting. The proposed method will allow us to
match the reconstructed face images with those
pictures taken from a surveillance camera. So we
believe this experiment setting will yield results
which are more strongly related with the one we
would get in real world application.
3.1 Matching Process
The procedure for training phase is illustrated in
Figure 2. Basically we can summarize it into
following steps. Given a set of face images and their
corresponding sketch images:
(1) Form a new hybrid face-sketch subspace by
appending every sketch to the end of the
corresponding face image.
(2) Perform eigen-analysis to calculate the
eigenvectors of the covariance matrix of the
face-sketch data
(3) The pseudo-eigensketches are obtained by
clipping off the upper half of eigenvectors
of the hybrid subspaces.
The procedure for reconstruction phase is
illustrated in Figure 4. Basically we can summarize
it into following steps:
(1) For each probe sketch image, we would
like to calculate the projection coefficient
P
s
when it is projected on
pseudo-eigensketch subspace. We use
least-squares fitting method to estimate
these projection coefficients given a test
face sketch.
(2) After we estimate the P
s
linear combination
coefficients, we use these with face
eigenvectors in hybrid subspace to
synthesize reconstructed face image in
hybrid subspace.
(3) Reconstructed face image is obtained by
keeping the upper half of the reconstructed
image in hybrid subspace.
In recognition phase, we do the following steps:
(1) Build an OTSDF correlation filter for each
reconstructed face image from the probe
sketch image.
(2) Use the CMU PIE illumination variation
face images of each person as testing face
images template and matches this OTSDF
filter with each of them to get PCE score.
(3) Classify the reconstructed image as the
person with whom the resulting PCE score
is the highest.
(4) For recognition with
one-nearest-neighbour method (1NN), we
calculate the Euclidean distance between
the reconstructed face image and testing
template, classify the reconstructed face
image as the person with whose training
image it has the shortest distance.
3.2 Result
In order to see the performance of the proposed
method, we contrast it with 1NN classifier.
Moreover, we also use different number of
eigenfaces to see if the proposed method degraded
gracefully when the quality of reconstructed images
is getting worse. In addition, all the experiment
results are based on the first rank, i.e: we only take
the one with the highest score, both OTSDF and
1NN. Figure 9 shows the result.
FACE RECOGNITION FROM SKETCHES USING ADVANCED CORRELATION FILTERS USING HYBRID
EIGENANALYSIS FOR FACE SYNTHESIS
17

Figure 9: Classification rate with OTSDF and 1NN.
10%
20%
30%
40%
50%
60%
70%
80%
90%
100%
10% 20% 30% 40% 50% 60% 70% 80% 90% 100%
Percentage of eigenvectors in hybrid space used for reconstruction
OTSDF on Light
1NN on Light
OTSDF on NoLight
1NN on NoLight
3.3 Conclusion
The experimental results obtained are very
encouraging. When experimenting on PIE Light
database, which is a relatively easier task, we can get
100% recognition rate with either the OTSDF or
1NN method. However, OTSDF can achieve 100%
even when only 30% of eigenvectors are used, while
the 1NN can only achieve recognition rate of
87.69%.
When experimenting on the CMU PIE NoLight
dataset, which is a much more challenging task, the
OTSDF approach clearly outperformed 1NN in all
experiments clearly showing its capabilities to
perform illumination tolerant face recognition. From
these experimental results, we can conclude that our
proposed novel face synthesis from sketch approach
coupled with advanced correlation filters for face
recognition is a successful solution to this problem
and is more feasible to work in real world system
than the latest work proposed by (Tang, 2002, 2004).
4 FUTURE WORK
We are working to evaluate our algorithm on a
larger dataset such as the Notre Dame Face
Recognition Grand Challenge (Phillips, 2004) to see
how the proposed method performs in large scale
face database.
REFERENCES
W. Zhao, R. Chellappa, A. Rosenfeld and P. J. Phillips,
“Face Recognition: A Literature Survey”, CS-Tech
Report-4167, University of Maryland, 2000.
X. Tang and X. Wang, “Face Photo Recognition Using
Sketch”, Proc. of Int. Conf. Image Processing, 2002.
X. Tang and X. Wang, “Face Sketch Recognition”, IEEE
Trans. on Circuit System and Video Technology,
Vol.14, pp.50-57, 2004.
X. Tang and X. Wang, “Face Sketch Synthesis and
Recognition”, Proc. of Int. Conf. Computer Vision,
2003.
Q. Liu, X. Tang, H, Jin, H. Lu, and S. Ma, “A Nonlinear
Approach for Face Sketch Synthesis and Recognition”,
Proc. Of. IEEE Computer Society Conference on
Computer Vision and Pattern Recognition, 2005.
M.A. Turk and A. P. Pentland, “Face recognition using
eigenfaces”, presented at Computer Vision and Pattern
Recognition, 1991. Proceeding CVPR ’91., IEEE
Computer Society Conference on, 1991.
B.V.K. Vijaya Kumar, “Tutorial Survey of Composite
Filter designs for Optical Correlators,” Applied Optics,
vol. 31, pp. 4773-4801, 1992
A. Mahalanobis, B.V.K. Vijaya Kumar, and D. Casasent,
“Minimum average correlation energy filters,”
Applied Optics, vol. 26:3633-3640, 1987.
A. Mahalanobis, B.V.K. Vijaya Kumar, S. Song, S.R.F.
Sims, and J.F. Epperson, “Unconstrained correlation
filters,” Applied Optics, vol. 33:3751-3759, 1994.
B. V. K. V. Kumar, D. Carlson, and A. Mahalanobis,
“Optimal tradeoff synthetic discriminant function
(OTSDF) filters for arbitrary devices,” Opt. Lett., vol.
19, pp. 1556–1558, 1994.
P. J. Phillips, H. Moon, P. J. Rauss, and S. Rizvi, "The
FERET evaluation methodology for face recognition
algorithms", IEEE Transactions on Pattern Analysis
and Machine Intelligence, Vol. 22, No. 10, October
2000.
P. J. Phillips, P. J. Rauss, and S. Z. Der, " FERET (Face
Recognition Technology) Recognition Algorithm
Development and Test Results", October 1996. Army
Research Lab technical report 995.
P. J. Phillips, “Face Recognition Grand Challenge”,
presented at Biometric Consortium Conference, 2004
T. Sim, S. Baker, and M. Bsat “The CMU Pose,
Illumination, and Expression (PIE) Database of
Human faces,” Tech. Report CMU-RI-TR-01-02,
Robotics Institute, Carnegie Mellon University,
January (2001)
M. Savvides, B.V.K. Vijaya Kumar and P.K. Khosla,
"Robust, Shift-Invariant Biometric Identification from
Partial Face Images", Biometric Technologies for
Human Identification (OR51) 2004.
M. Savvides, B.V.K. Vijaya Kumar and P.K. Khosla,
“Face verification using correlation filters”, Proc. Of
the Third IEEE Automatic Identification Advanced
Technologies, 56-61, Tarrytown, NY, March 2002.
M. Savvides, C.Xie, N. Chu, B.V.K.Vijaya Kumar, C.
Podilchuk, A. Patel, A. Harthattu, R. Mammone,
“Robust Face Recognition using Advanced
Correlation Filters with Bijective-Mapping
Preprocessing”, Audio-Video Based Biometric Person
Authentication (AVBPA), July 2005.
ICEIS 2006 - HUMAN-COMPUTER INTERACTION
18
