
SMOOTH BLOCKS-BASED BLIND WATERMARKING
ALGORITHM IN COMPRESSED DCT DOMAIN
Chun Qi, Haitao Zhou, Bin Long
Institute of Image Processing & Recognition, Xi’an Jiaotong University, 710049Xi’an, China
Keywords: Smooth blocks, Blind Watermarking, DCT, Weber’s Law, JPEG domain.
Abstract: A novel blind watermarking scheme based on smooth blocks in compressed DCT domain is proposed. The
smooth blocks are detected by a criterion which uses a relation between the quantized DC coefficients and
the variance of AC coefficients in the block and deduced from the Weber’s Law. In the approach, the
watermark is embedded by modifying the average value of some low-frequency DCT coefficients in
selected blocks, and recovered by the sign of the mean value of corresponding coefficients in detected
blocks and there is no need for original image. The experimental results demonstrate that almost no
perceptible distortion is found in the watermarked images, and the watermark is robust to some image
processing operations such as scaling, noise, filtering and JPEG compression.
1 INTRODUCTION
Many DCT-based watermarking schemes have been
proposed as a solution to the copyright protection of
multi-media recently. Suhail et al propose a digital
watermarking based on image segmentation (Suhail,
2003). Peter Wong et al hide data only in the texture
blocks (Wong, 2001). In block-based algorithms,
good care must be taken to avoid smooth (or non-
textured) blocks and edge blocks as modification of
these leads to annoying artifacts in the watermarked
image (Holliman, 1998).
Actually, we find that if we do some changes to
the low-frequency DCT coefficients of appropriate
smooth block, perceptible distortions would be
hardly found in the watermarked images. Moreover,
the watermark inserted in these smooth blocks is
robust to some image processing operations such as
filtering and JPEG compression. In this paper we
develop a new watermarking algorithm based on the
smooth blocks. A criterion is presented according to
the Weber’s Law to select these blocks. Different
tests are conducted to verify the performance of the
scheme under different types of attacks. The method
appears to be very robust to most image processing
operations. The paper is organized as follows.
Section 2 describes the embedding and extracting
techniques in details and Section 3 elaborates
various experimental results. Finally, Section 4 gives
the conclusions.
2 PROPOSED WATERMARKING
TECHNIQUE
In this section we describe our watermarking scheme
in detail, which is block-based and shares same
features with the JEPG standard for still image
compression. The quantized DC and the AC
coefficients denote the average luminance and the
different frequency band of a block which could
reflect its texture respectively (Jianmin, 2002). A
new approach to select the appropriate smooth
blocks is given as follows:
2.1 Classifying Smooth blocks
In this paper, we introduce a similar criterion (Lin,
2005
) based on the quantized DC coefficients and
variance of AC coefficients, which is deduced from
the well-known Weber’s Law (Gonzalez, 2002).
02.0≈
Δ
I
I
(1)
Where
I
Δ
denotes the object, and
I
denotes the
background. This equation is true only when the
range of
I
is in the middling intensity, which is
clearly shown in the Fig.1. The proposed classified
method bears a resemblance to the Weber’s Law:
Considering the average luminance and the texture
of a block as the background and the object mention-
347
Qi C. and Zhou H. (2006).
SMOOTH BLOCKS-BASED BLIND WATERMARKING ALGORITHM IN COMPRESSED DCT DOMAIN.
In Proceedings of the International Conference on Security and Cryptography, pages 347-350
DOI: 10.5220/0002098803470350
Copyright
c
SciTePress

Figure 1: Weber curve.
ed in the Weber’s Law, respectively. We can get a
similar equation from Eq. (1):
02.0≈
DC
σ
(2)
Where DC is the quantized DC coefficients of a
block, and
σ
is the standard deviation of all the AC
coefficients in a block.
The Weber ratio mentioned in formula (2) is just a
critical value which can be used for classifying
blocks. Then we can get a general formula to select
the smooth blocks apart from other blocks.
DC×≤ 02.0
σ
(3)
We can get an easy formula as follows after squaring
the both side
2
)02.0()var( DCAC ×≤
(4)
Where
)var( AC
and DC are the variance of the 63
quantized AC coefficients and the quantized DC
coefficient of a block, respectively.
In order to avoid selecting texture blocks we
should strictly choose the number of the smooth
blocks to improve this method. Here we adopt a
variable instead of the constant value 0.02 as the
following formula:
2
)()var( DCAC ×≤
α
(5)
Where
α
is an adaptive value according to the
feature of the image and
02.0
≤
α
.
However, some high intensity blocks are so
sensitive that they are not fit for watermark
embedding, which would cause severe visual
artefacts. Hence, a formula is given for excluding
these high intensity blocks as follows:
02.0
_
α
×≤ grayaverDC
(6)
Where
g
ra
y
ave
r
_
denotes the average gray-scale of
the whole image.
As lower luminance blocks are less sensitive to
human eyes as can be seen from Fig.1, we should
reserve these lower intensity blocks which are
appropriate for embedding:
If
30
<
DC
,
30=DC
(7)
Where the modified DC is just used for computation,
in some sense, and the original DC is recovered
when the selection of the block is completed.
2.2 Selecting Smooth Blocks
Smooth blocks are selected depending on formula
(5), (6) and (7). The number of smooth blocks we
choose is based on the size and characteristic of the
image. The detail steps of selecting appropriate
smooth blocks are described as follows:
1) First set
0
=
α
, and set n=0, where n is the
number of actually selected blocks.
2) The
α
is gradually increased by a step of
00025.0
=
Δ
α
, and
02.0
≤
α
. According to the
formula (5), (6) and (7). Record the value of
n
when
α
is increasing.
3) Thirdly, the loop is continued if
02.0
≤
α
and
Nn
≤
. Or, the loop is terminated. Then
n
selected blocks are obtained.
Appropriate blocks are selected according to the
three steps mentioned above. The number of selected
blocks is determined by the adaptive factor
α
and no
less than N=200, decided empirically, while the total
blocks of the standard image are 1024.
2.3 Watermark Embedding
Let
X
be an original gray-level image of size
21
NN ×
,
and the watermark w be a random bipolar binary
sequence that uniformly from{1,-1}, of which the
length is
64/)(
21
NNL
×
=
. During insertion,
X
is
performed
88
×
DCT. Then the quantized DCT
coefficients are sorted in zigzag order.
),( jiF
denotes
the j
th
quantized coefficients in zigzag order of the i
th
88
×
block. Three steps for embedding are as follows:
1) Choose the smooth blocks depending on the
Section 2.2. In this situation, we should promote
0005.0
=
Δ
α
, so that we could selected more
blocks than that of the extracting.
2) Assume the i
th
88
×
block is the smooth block that
we choose. Considered the robustness and invisi-
SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY
348

bility, the coefficients for modification are
)2,(iF
,
)3,(iF
,
)5,(iF
empirically. The average value of
the three coefficients:
3/)]5,()3,()2,([_ iFiFiFACaver +
+
=
(8)
If the watermark
1)(
=
=iw
, we should promote
the average value to the positive. The details are
as follows:
if
1_ ≥ACaver
, do not need to modify;
else if
1_0 <≤ ACaver
,
)_1(),(),(' ACaverjiFjiF −
+
=
(9)
Where
),(' jiF
is the modified coefficient, j=2, 3, 5.
else,
0_ <ACaver
,
)_(),(),(' ACaverfloorjiFjiF
−
=
(10)
Where floor(*) denotes the maximum integer that
is less than (*), and j=2, 3, 5.
If the watermark
1)( −
=
=iw
, we should demote
the average value to the negative. The details are
as follows:
if
1_ −≤ACaver
, do not need to modify;
else if
0_1 ≤<− ACaver
,
)_1(),(),(' ACaverjiFjiF −−+=
(11)
else
0_ >ACaver
,
)_(),(),(' ACaverceiljiFjiF
−
=
(12)
Where ceil(*) is the minimum integer that is
greater than (*), and j=2, 3, 5.
3) Repeat Step-2 until selected blocks are embedded
with watermarks. For the non-selected blocks, the
corresponding watermarking bit has no need to be
inserted. Then perform inverse DCT for those
blocks and finally obtain the watermarked image.
2.4 Watermark Extraction
The watermark extracting can be performed without
knowledge of the original image. Here are the steps
as follows:
1) Perform DCT compressed for each
88
×
block.
Select n blocks as mentioned in Section 2.2. Here
the
00025.0=Δ
α
is less than that of the inserting,
so some embedded blocks will be excluded as
the step halved of that of the embedding. We can
extract the information from these blocks.
2) For each selected block, the average of some
coefficients is computed as follows:
3/)]5,(')3,(')2,('['_ iFiFiFACAver +
+
=
(13)
Where
'_ ACAver
denotes the average value of
the three quantized AC coefficients, and
),(' jiF
denotes the j
th
quantized coefficients in
zigzag scanning order of the i
th
88×
block in the
watermarked image. The detected watermarking
bits are extracted according to sign of the average
value:
)'_()(' ACAversigniw
=
(14)
Where w’(i) indicate the extracted watermark,
and sign(*) is signed function.
For non-selected blocks such as those edge and
texture blocks, while the one is the
th
i
block of
the whole blocks, we set the corresponding
detected watermark information:
0)('
=
iw
. (15)
Repeat this step for every block till the whole
detected watermarking sequence is obtained.
Then we can get the extracted watermark
sequence w’ from {1, 0, -1}, with the length of L
the same as the number of all the blocks. When
the detected watermark is from {1, -1}, it means
we get the valid watermark information; else if
is {0}, the corresponding watermark bit is useless.
3) To evaluate the similarity of the extracted and
the original, we measure the similarity by the
following correlation function :
∑∑
==
=
L
i
L
i
iwiwiwNC
1
2
1
)('/)(')(
(16)
Where L is the length of the watermark sequence,
which is same as the number of the whole blocks,
w(i) is the original watermark and w’(i) is the
extracted. NC is the normalized correlation,
which range from -1 to 1. If NC>T, it implies that
there is a watermark existing in the testing image,
where T is an experimental value.
3 EXPERIMENTAL RESULTS
Several common image processing operations and
geometric distortions were applied to these images
to evaluate whether the correlation output of detector
SMOOTH BLOCKS-BASED BLIND WATERMARKING ALGORITHM IN COMPRESSED DCT DOMAIN
349
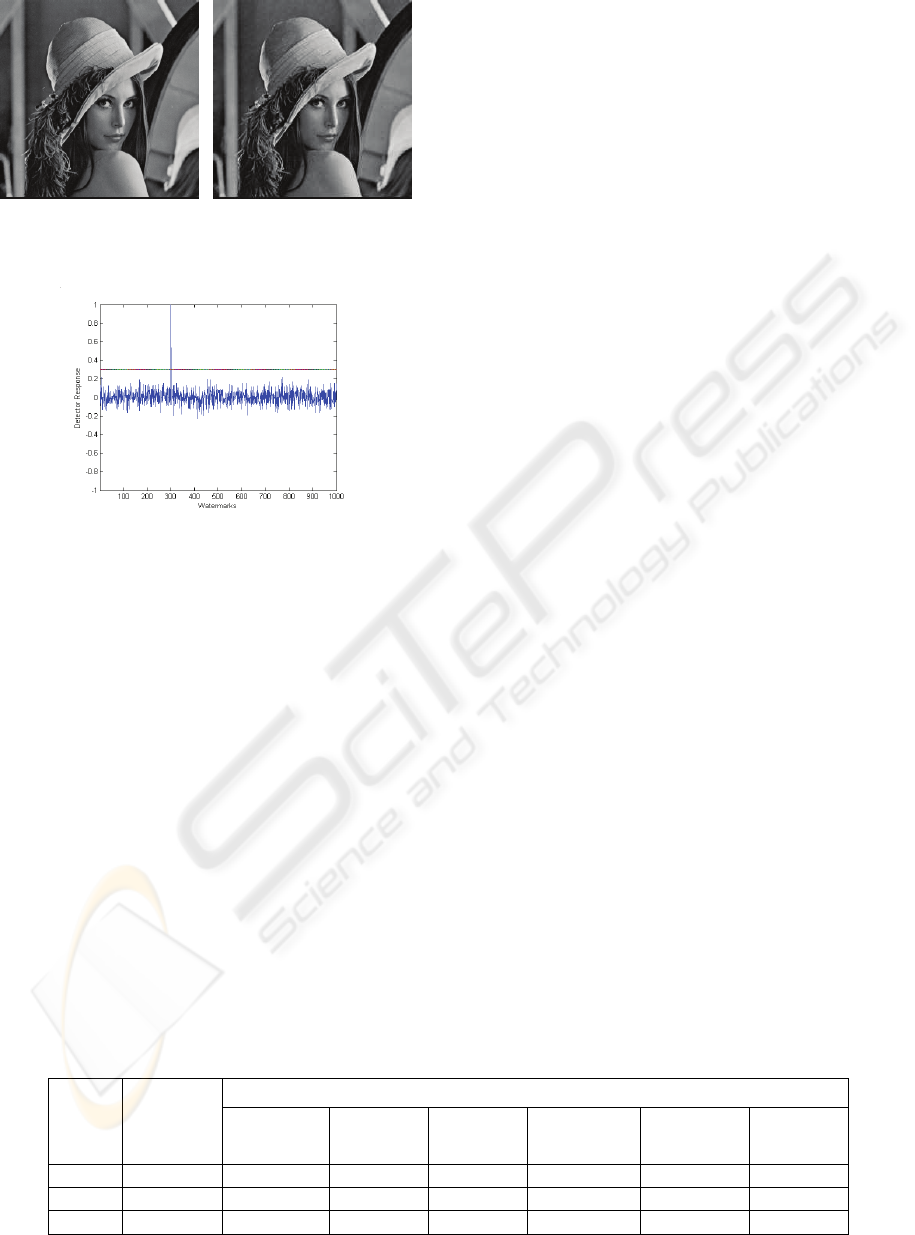
Figure 2: Original (right) and watermarked “Lena”(left) ,
PSNR=31.89db.
Figure 3: Bipolar detector output for Lena image, NC=1.00.
can reveal the existence of watermarking in the
images. Here we only show the result of “Lena” in
detail. Fig.2 shows both the original and the
watermarked images. Fig.3 illustrates uniqueness of
the watermark. The response of a given mark is
compared to
T
(
3.0=T
, an experimental value) to
decide whether the watermark is present or not.
Some attacks such as common image processing
operations and geometric distortions, are described
in Table 1. The check threshold is T=0.3. Due to the
space limitation of the paper, many other detailed
results and discussions are omitted. As shown in the
table, it can be indicated that the correlation output
is 1.0 for the three images when attack-free, and
PSNR is also appropriate, and both PSNR and NC
will drastically decline when the watermarked
images have some distortions. But NC is always no
less than the threshold (T=0.3), which means that the
watermark can be correctly detected even there are
some distortions. From this table, the robustness of
proposed scheme could be demonstrated.
4 CONCLUSION
Avoiding modifying smooth (or non-textured)
blocks and edge blocks during the watermarking
process is a traditional view. This paper proposes an
idea that watermarking can be embedded in smooth
blocks. Experimental results show that this technique
is robust to many standard image processing
operations and some geometric distortions. It is
clearly that robustness against median filtering and
Gaussian noise was achieved when the watermarked
images were seriously degraded. Some geometric
attacks can be resisted by the scheme. Moreover, the
proposed method doesn’t need to use the original
images during extracting watermark. In addition, the
proposed technique can also be extended to insertion
of invisible watermarks in digital video.
REFERENCES
M.A. Suhail, M.S., 2003. Digital watermarking-based
DCT and JPEG model. IEEE Trans. on Instrumenta-
tion and Measurements.
P.H. Wong, Au., 2001. A data hiding technique in JPEG
domain compressed domain. Proceeding of SPIE Conf.
of Security and Watermarking Multimedia Contents.
M. Holliman, N., 1998. Adaptive public watermarking of
DCT-based compressed images. Proc. Of SPIE-The
international society for optional engineering.
Jianmin J., G., 2002. The spatial relationship of DCT
coefficients between a block and its sub-blocks. IEEE
Trans. on Signal Processing.
F. Lin, L.YanJun and et al, 2005. A fast fractal image
coding method using the characteristics of human
vision system in DCT domain. Journal Of Computer-
Aided Design & Computer Graphics.
R.C. Gonzalez and R.E. Woods, 2002. The book, Digital
Image Processing.
Table 1: (PSNR/Bipolar NC) of Watermarked Images Under Various Attacks.
Attacks(our threshold T=0.3)
Test
images
Water-
maked
images
Median filter
(
77 ×
)
Histogram
equalization
Gaussian
Noise
Affine
Transform
(
261261
×
)
Randomly
move lines
(
230230
×
)
Scale down
to 0.3 of it’s
Original size
Lena 31.89/1.00 24.77/0.44 15.80/0.84 24.04/0.65 19.80/0.54 22.21/0.86 22.49/0.49
Camera 31.19/1.00 22.34/0.53 18.28/0.51 24.41/0.64 18.71/0.56 21.97/0.80 21.90/0.63
Bridge 25.24/1.00 19.23/0.30 18.06/0.58 22.96/0.76 16.65/0.47 19.15/0.58 19.21/0.33
SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY
350
