
PARALLEL MULTIPLICATION IN F
2
n
USING CONDENSED
MATRIX REPRESENTATION
Christophe Negre
´
Equipe DALI, LP2A, Universit
´
e de Perpignan
avenue P. Alduy, 66 000 Perpignan, France
Keywords:
Finite field, multiplication, matrix representation, irreducible trinomial.
Abstract:
In this paper we explore a matrix representation of binary fields F
2
n
defined by an irreducible trinomial
P = X
n
+ X
k
+ 1. We obtain a multiplier with time complexity of T
A
+ (⌈log
2
(n)⌉)T
X
and space
complexity of (2n − 1)n AND and (2n − 1)(n − 1) XOR . This multiplier reaches the lower bound on time
complexity. Until now this was possible only for binary field defined by AOP (Silverman, 1999), which are
quite few. The interest of this multiplier remains theoretical since the size of the architecture is roughly two
times bigger than usual polynomial basis multiplier (Mastrovito, 1991; Koc and Sunar, 1999).
1 INTRODUCTION
A binary field F
2
n
= F
2
[X]/(P ) is a set of 2
n
ele-
ments in which we can do all the basic arithmetic op-
eration like addition, subtraction, multiplication and
inversion modulo an irreducible binary polynomial P .
Finite field arithmetic is widely used in cryptographic
applications (Miller, 1985) and error-correcting code
(Berlekamp, 1982). For these applications, the most
important finite field operation is the multiplication.
The representation of binary field elements have a
big influence on the efficiency of field arithmetic. Un-
til now, field elements were represented as sum of ba-
sis elements: the basis is composed by n elements
B
1
, . . . , B
n
∈ F
2
n
, in this situation an element U
in F
2
n
is written as U = u
1
B
1
, + · · · + u
n
B
n
with
u
i
∈ {0, 1}.
The most used bases are polynomial bases (Mas-
trovito, 1991; Koc and Sunar, 1999; Chang et al.,
2005) and normal bases (Wu and Hasan, 1998; Koc
and Sunar, 2001).
Our purpose here is to investigate a new represen-
tation: the matrix representation. We will focus on
field defined by a trinomial F
2
n
= F
2
[X]/(P ) with
P = X
n
+ X
k
+ 1. In the matrix representation an
element U of F
2
n
is represented by the n
2
coefficients
of a n × n matrix M
U
. The additions of two elements
U and V simply consists to add the two matrices M
U
and M
V
and to multiply U and V it consists to multi-
ply the matrix product M
U
· M
V
.
This gives a faster multiplication than multiplica-
tion using basis representation: a parallel multiplier
associated to a matrix representation has a time com-
plexity of T
A
+ (⌈log
2
(n)⌉)T
X
, whereas in basis rep-
resentation, for field defined by a trinomial (Koc and
Sunar, 1999; Mastrovito, 1991), the time complexity
is generally equal to T
A
+ (2 + ⌈log
2
(n)⌉)T
X
. The
major drawback of this method is due to the length of
the representation which requires n
2
coefficients, and
provides parallel multiplier with a cubic space com-
plexity in n. But if we carefully select a subset of the
matrix coefficients, the number of distinct coefficients
in each matrix M
U
becomes small: in our situation it
is equal to (2n − 1). In other words we condense the
matrix representation in (2n − 1) distinct coefficients
to decrease the space complexity.
The paper is organized as follows : in the first sec-
tion we recall the method of Koc and Sunar (Koc and
Sunar, 1999) for finite field multiplication modulo tri-
nomial. They perform the reduction modulo the trino-
mial on a matrix and then compute a matrix-vector to
get the product of two elements. In the second section
we study the possibility to use the matrix constructed
with Koc and Sunar’s method to represent finite field
elements. After that we evaluate the complexity of a
parallel multiplier in this matrix representation. Next,
we study a condensed matrix representation and the
associated multiplier. We finally give a small exam-
ple of our matrix multiplier and finish by a complexity
comparison and a brief conclusion.
254
Negre C. (2006).
PARALLEL MULTIPLICATION IN F2n USING CONDENSED MATRIX REPRESENTATION.
In Proceedings of the International Conference on Security and Cryptography, pages 254-259
DOI: 10.5220/0002096402540259
Copyright
c
SciTePress

2 MATRIX REPRESENTATION IN
POLYNOMIAL BASIS
Let P = X
n
+ X
k
+ 1 be an irreducible polynomial
in F
2
[X]. Without loss of generality we can assume
k ≤
n
2
since when X
n
+ X
k
+ 1 is irreducible, the
reciprocal polynomial X
n
+ X
n−k
+ 1 is also irre-
ducible. Furthermore, in this paper we will always
suppose for simplicity k ≥ 2.
An element U ∈ F
2
n
= F
2
[X]/(P ) is a polyno-
mial of degree n − 1. To compute the product of two
elements U and V in F
2
n
we first compute the product
of polynomial
W = UV =
n−1
X
i=0
u
i
X
i
!
n−1
X
i=0
v
i
X
i
!
. (1)
This product can be done by a matrix vector prod-
uct N
U
· V where N
U
is given below
1 →
X →
.
.
.
X
n−2
→
X
n−1
→
X
n
→
X
n−1
→
.
.
.
X
2n−2
→
X
2n−1
→
u
0
0 · · · 0 0
u
1
u
0
· · · 0 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
u
n−2
u
n−3
· · · u
0
0
u
n−1
u
n−2
· · · u
1
u
0
0 u
n−1
· · · u
2
u
1
0 0 · · · u
3
u
2
.
.
.
.
.
.
.
.
.
0 0 · · · 0 u
n−1
0 0 · · · 0 0
.
The product W = UV contains monomials X
i
with larger degree than n, i.e., with n ≤ i ≤ 2n − 2.
These monomials must be reduced modulo P =
X
n
+ X
k
+ 1. To perform this reduction we will
use the following identity modulo P for each i ≥ n
X
i
= X
i−(n−k)
+ X
i−n
mod P. (2)
For example if P = X
5
+X
2
+1 then we have X
5
=
X
2
+ 1 mod P and in the same way X
6
= X
3
+ X
mod P and so on.
Koc and Sunar in (Koc and Sunar, 1999) have pro-
posed to perform the reduction modulo P on the line
of the matrix N
U
instead of performing the reduction
on the polynomial W = UV .
To describe this reducing process we need to state
some notations. If M is a n × 2n matrix, we denote
by (M )
t
the top part of the matrix M constituted by
the n first lines. We will denote also (M )
l
the matrix
constituted by the n last lines. And finally, we will
denote M[↑ s] the matrix shifted up by s rows from
M, and M[↓ s] the matrix shifted down by s rows.
From equation (2) the line corresponding to X
i
for
i ≥ n are pushed up to the lines corresponding to
X
i−n
and X
i−n+k
. Using the previous notation, this
procedure modifies the matrix N
U
as follows
(N
U
)
t
← (N
U
)
t
+ (N
U
)
l
+ (N
U
)
l
[↓ k] (3)
(N
U
)
l
← (N
U
)
l
[↑ (n − k)] (4)
If we denote by S the low part of N
U
, and by T the
top part of N
U
S =
0 u
n−1
u
n−2
· · · u
1
0 0 u
n−1
· · · u
2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 0 · · · u
n−1
0 0 0 0 0
, T =
u
0
0 · · · 0
u
1
u
0
· · · 0
.
.
.
.
.
.
.
.
.
u
n−1
u
n−2
· · ·u
0
,
we can rewrite equation (3) and (4) as
(N
U
)
t
= T + S + S[↓ k],
(N
U
)
l
= S[↑ (n − k)].
(5)
Now, since we assumed k ≥ 2, in the
new expression of N
U
, the lines corresponding
to X
n
, . . . , X
n+k−2
contains non-zero coefficients.
Thus, we have to reduce a second time N
U
with the
same method. We set S
′
= S[↑ (n − k)] = (N
U
)
l
and the second reduction provides
(N
U
)
t
= T + S + S
′
+ (S + S
′
)[↓ k]
(N
U
)
l
= 0.
(6)
We finally have the expression of M
U
= (N
U
)
t
the
reduced form of N
U
M
U
=
u
0
u
n−1
· · · · · · · · · u
k
u
′
k−1
. . . . . . u
′
1
u
1
u
0
u
n−1
· · · · · · · · · u
k
u
′
k−1
. . . u
′
2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
u
k−2
· · · · · · u
0
u
n−1
· · · · · · · · · u
k
u
′
k−1
u
k−1
u
k−2
· · · · · · u
0
u
n−1
· · · · · · · · · u
k
u
k
u
′
k−1
u
′
k−2
· · · · · · u
′
0
u
′′
n−1
· · · · · · u
′′
k+1
u
k+1
u
k
u
′
k−1
· · · · · · · · · u
′
0
u
′′
n−1
· · · u
′′
k+2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
u
n−2
· · · · · · u
k
u
′
k−1
· · · · · · · · · u
′
0
u
′′
n−1
u
n−1
· · · · · · · · · u
k
u
′
k−1
· · · · · · · · · u
′
0
,
(7)
where
u
′
i
= u
i
+ u
i+(n−k)
for 0 ≤ i < k,
u
′′
i
=
u
i
+ u
i−k
+ u
i+n−2k
for k ≤ i < 2k,
u
i
+ u
i−k
for 2k ≤ i < n.
The method of Koc and Sunar (Koc and Sunar,
1999) to compute the product UV mod P , first con-
sists to compute the coefficients u
′
i
and u
′′
i
of M
U
and
after that to perform the matrix-vector product M
U
·V
to obtain U V mod P . This multiplier computes the
product in time T
A
+ (⌈log
2
(n)⌉ + 2)T
X
using a par-
allel architecture.
If we know the coefficients u
i
, u
′
i
and u
′′
i
we avoid
the delay to compute these coefficients. In this sit-
uation the product could be done in time T
A
+
PARALLEL MULTIPLICATION IN F2n USING CONDENSED MATRIX REPRESENTATION
255

⌈log
2
(n)⌉T
X
. This remark pushed us to try to keep
the field elements U ∈ F
2
n
expressed by the matrix
M
U
(i.e., in this case we always know the coefficients
u
i
, u
′
i
and u
′′
i
, and we don’t have to compute it before
the multiplication) and try to use this representation
to implement finite field arithmetic.
Definition (Matrix Representation). Let F
2
n
=
F
2
[X]/(P ) where P = X
n
+ X
k
+ 1 with 2 ≤
k ≤
n
2
. The matrix representation of an element
U =
P
n−1
i=0
u
i
X
i
of the field F
2
n
is the matrix given
in equation (7) expressed in term of the coefficients
u
i
, u
′
i
and u
′′
i
.
The next section is devoted to explain how to add
and multiply field elements in matrix representation.
3 FIELD ARITHMETIC IN
MATRIX REPRESENTATION
Let F
2
n
= F
2
[X]/(P ) where P is an irreducible tri-
nomial P = X
n
+ X
k
+ 1 with 2 ≤ k ≤
n
2
.
The following Theorem shows that, if the elements
U ∈ F
2
n
are represented by their associated matrix
M
U
, finite field arithmetic corresponds to classical
n × n matrix arithmetic.
Theorem 1. Let F
2
n
= F
2
[X]/(P ) where P is an
irreducible trinomial P = X
n
+ X
k
+ 1 with 2 ≤
k ≤
n
2
. Let U =
P
n−1
i=0
u
i
X
i
and V =
P
n−1
i=0
v
i
X
i
be two elements in F
2
n
and M
U
and M
V
their cor-
responding matrix defined in (7). If W
1
= U + V
mod P and W
2
= UV mod P we have
M
W
1
= M
U
+ M
V
, (8)
M
W
2
= M
U
· M
V
. (9)
Proof. Using equation 7, it is clear that to show the
assertion for W
1
, it is sufficient to show that
w
i
= u
i
+ v
i
,
w
′
i
= u
′
i
+ v
′
i
,
w
′′
i
= u
′′
i
+ v
′′
i
.
The identity on w
i
is trivial since W
1
= U + V
mod P . For w
′
i
we have
w
′
i
= w
i
+w
i+(n−k)
= (u
i
+v
i
)+(u
i+(n−k)
+v
i+(n−k)
).
By rearranging this expression, we get
w
′
i
= (u
i
+ u
i+(n−k)
) + (v
i
+ v
i+(n−k)
) = u
′
i
+ v
′
i
.
A similar proof can be done to show that w
′′
i
= u
′′
i
+
v
′′
i
.
For the assertion on M
W
2
it is a little bit more dif-
ficult. We remark that from the result of section 2, for
every elements Z ∈ F
2
n
the product V Z in F
2
n
is
given by M
V
· Z and the product W
2
Z by M
W
2
· Z.
Thus we get for every Z ∈ F
2
n
that
M
W
2
· Z = W
2
Z = U V Z
= M
U
· (V Z) = M
U
· (M
V
· Z)
= (M
U
· M
V
) · Z
This implies that (M
W
−M
U
M
V
)·Z = 0 for each
Z in F
2
n
, but this means that (M
W
− M
U
M
V
) is the
zero matrix. In other words we have M
W
= M
U
·M
V
as required.
For a more general proof see (Lidl and Niederreiter,
1986). The following example illustrates the Theo-
rem 1.
Example 1. We consider the field F
2
7
=
F
2
[X]/(X
7
+ X
3
+ 1) and let U =
P
n−1
i=0
u
i
X
i
be
an element of F
2
7
. From equation (7) we get the fol-
lowing expression of M
U
M
U
=
u
0
u
6
u
5
u
4
u
3
u
′
2
u
′
1
u
1
u
0
u
6
u
5
u
4
u
3
u
′
2
u
2
u
1
u
0
u
6
u
5
u
4
u
3
u
3
u
′
2
u
′
1
u
′
0
u
′′
6
u
′′
5
u
′′
4
u
4
u
3
u
′
2
u
′′
1
u
′
0
u
′′
6
u
′′
5
u
5
u
4
u
3
u
′
2
u
′
1
u
′
0
u
′′
6
u
6
u
5
u
4
u
3
u
′
2
u
′
1
u
′
0
with u
′
0
= u
0
+ u
4
, u
′
1
= u
1
+ u
5
, u
′
2
= u
2
+ u
6
and
u
′′
4
= u
′
4
+u
1
+u
5
, u
′′
5
= u
5
+u
2
+u
6
, u
′′
6
= u
6
+u
3
.
For U = 1 + X + X
4
and V = X
2
+ X
3
+ X
5
we
obtain the following matrices
M
U
=
1 0 0 1 0 0 1
1 1 0 0 1 0 0
0 1 1 0 0 1 0
0 0 1 0 0 0 0
1 0 0 1 0 0 0
0 1 0 0 1 0 0
0 0 1 0 0 1 0
, M
V
=
0 0 1 0 1 1 1
0 0 0 1 0 1 1
1 0 0 0 1 0 1
1 1 1 0 1 0 1
0 1 1 1 0 1 0
1 0 1 1 1 0 1
0 1 0 1 1 1 0
.
Now we add M
U
and M
V
to get the matrix M
W
1
=
M
U
+ M
V
of W
1
= U + V = X
5
+ X
4
+ X
3
+
X
3
+ X + 1 mod P and we multiply M
U
and M
V
to get the matrix M
W
2
= M
U
· M
V
of W
2
= UV =
X
4
+ X
3
+ 1 mod P
M
W
1
=
1 0 1 1 1 1 0
1 1 0 1 1 1 1
1 1 1 0 1 1 1
1 1 0 0 1 0 1
1 1 1 0 0 1 0
1 1 1 1 0 0 1
0 1 1 1 1 0 0
, M
W
2
=
1 0 0 1 1 0 0
0 1 0 0 1 1 0
0 0 1 0 0 1 1
1 0 0 0 1 0 1
1 1 0 0 0 1 0
0 1 1 0 0 0 1
0 0 1 1 0 0 0
.
4 PARALLEL MULTIPLICATION
IN MATRIX REPRESENTATION
Let us now study the architecture of the multiplier as-
sociated to the matrix representation. We fix U, V ∈
SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY
256

F
2
n
and M
U
and M
V
their associated matrix. Let
W = UV be the product of U and V in F
2
n
and
M
W
its associated matrix . We will note L
i
(M
U
) for
i = 0, . . . , n − 1 the line of M
U
and C
j
(M
V
) for
j = 0, . . . , n − 1 the columns of M
V
.
The coefficient Coeff
i,j
(M
W
) of index (i, j) of
M
W
is then computed as a line-column matrix prod-
uct (in the sequel we will call this operation a scalar
product)
Coeff
i,j
(M
W
) = L
i
(M
U
) · C
j
(M
V
)
=
P
n−1
ℓ=0
Coeff
i,ℓ
(M
U
)Coeff
ℓ,j
(M
V
)
(10)
A scalar product (10) can be done in time T
A
+
⌈log
2
(n)⌉T
X
, where T
A
is the delay for an AND gate
and T
X
for an XOR gate, using parallel AND gates
and a binary tree of XOR.
Consequently, if all these scalar products are done
in parallel, one can compute the product M
W
of M
U
and M
V
in time T
A
+ ⌈log
2
(n)⌉T
X
. So at this point
we reach the lower bound on time complexity in bi-
nary field multiplication.
The major drawback of this approach is that
we have to compute n
2
coefficients Coeff
i,j
(M
W
).
The space complexity is thus roughly n
3
AND and
n
3
XOR which is widely too big and not practical.
But in fact, we did not use the fact that the number
of distinct coefficients in each matrix M
U
, M
V
and
M
W
is quite small. A lot of scalar products can be
avoided, this motivates the use of a condensed matrix
representation.
5 CONDENSED MATRIX
REPRESENTATION
The set of coefficients of the matrix M
U
for a given U
is quite small: it consists of the n bits u
i
, the k bits u
′
i
and the (n− k − 1) bits u
′′
i
. The matrix representation
M
U
can be condensed in this three set of coefficients.
Definition (Condensed Matrix Representation). We
consider the field F
2
n
= F
2
[X]/(P ) where P is an
irreducible trinomial, and let U =
P
n−1
i=0
u
i
X
i
be an
element of F
2
n
. The condensed matrix representation
of U is CMR(U) = (U, U
′′
, U
′′′
) such that
U = (u
0
, . . . , u
n−1
),
U
′
= (u
′
0
, . . . , u
′
k−1
), where u
′
i
= u
i
+ u
i+(n−k)
,
U
′′
= (u
′′
i
, . . . , u
′′
j
), where
• u
′′
i
= u
i
+ u
i−k
+ u
i+n−2k
for i = k +
1, . . . , 2k − 1,
• u
′′
i
= u
i
+ u
i−k
for i = 2k, . . . , n − 1.
The condensed matrix representation of U contains
all the distinct coefficients of the matrix M
U
. We can
thus reconstruct each line and each column of matrix
M
U
.
Construction of the lines of M
U
. We note L
i
(M
U
)
the line of M
U
for i = 0, . . . , n − 1. Using the
expression of M
U
of equation (7), we get the fol-
lowing expression of these lines of M
U
in term of
the CMR of U in the Table 1.
Table 1: Lines of M
U
.
i=0,...,k−2 L
i
(M
U
)=
[
u
i
u
i−1
···u
0
u
n−1
···u
k
u
′
k−1
...u
′
i+1
]
i=k−1 L
k−1,A
=
[
u
k−1
u
k−2
···u
0
u
n−1
···u
k
]
i=k,...n−2 L
i
(M
U
)=
[
u
i
...u
k
u
′
k−1
...u
′
0
u
′′
n−1
...u
′′
i+1
]
i=n−1 L
i
(M
U
)=
[
u
n−1
...u
k
u
′
k−1
...u
′
0
]
Construction of the columns of M
U
. We note
C
j
(M
U
) the columns of M
U
for j = 0, . . . , n − 1.
From (7) we get the Table 2 of the columns of M
U
where the expression of C
j
(M
U
) are given in term
of the CM representation of U.
Now using these descriptions of the lines and the
columns of the matrix M
U
we can easily express the
multiplication in the condensed matrix representation.
5.1 Multiplication in Condensed
Matrix Representation
Let U and V be two elements of F
2
n
given
by their respective condensed matrix representa-
tion CMR(U) = (U, U
′
, U
′′
) and CMR(V ) =
(V, V
′
, V
′′
). As stated in the previous section, with
the CMR representation of U and V we can easily
construct the lines and columns of M
U
and M
V
. We
want to compute the coefficients of the condensed
matrix representation of the product W = U V in
F
2
n
= F
2
[X]/(X
n
+ X
k
+ 1). To do this first re-
call that, from Theorem 1, for each 0 ≤ i, j ≤ n − 1
we have
Coeff
i,j
(M
W
) = L
i
(M
U
) · C
j
(M
V
). (11)
To get the CMR of W we need only to compute the
coefficients W, W
′
, W
′′
of M
W
.
• Computing the coefficients of W . The coefficients
w
i
of CMR(W ) are in the first column of M
W
.
This means that
w
j
= Coeff
0,j
(M
W
) = L
0
(M
U
) · C
j
(M
V
).
• Computing the coefficients of W
′
and W
′′
. If we
look at equation (7) we can see that W
′
and W
′′
appears in the line L
k
(M
W
), i.e.,
w
′
j
= Coeff
k,j
(M
W
) for 1 ≤ j ≤ k,
w
′′
j
= Coeff
k,j
(M
W
) for k + 1 ≤ j ≤ n − k.
PARALLEL MULTIPLICATION IN F2n USING CONDENSED MATRIX REPRESENTATION
257

Table 2: The columns of M
U
.
j = 0 C
0
(M
U
) =
t
[
u
0
· · ·· · ·· · ·u
n−1
]
j = 1, . . . , k − 1 C
j
(M
U
) =
t
u
n−j
· · ·u
n−1
u
0
· · ·u
k−j−1
u
′
k−j
· · ·u
′
k−1
u
k
· · ·u
n−j−1
j = k, . . . , n − k C
j
(M
U
) =
t
u
n−j
· · ·u
n−j+k−1
u
′′
n−j+k
· · ·u
′′
n−1
u
′
0
· · ·u
′
k
u
k+1
· · ·u
n−j−1
j = n − k + 1, . . . , n − 1 C
j
(M
U
) =
t
u
′
n−j
· · ·u
′
k−1
u
k
· · ·u
n−j+k−1
u
′′
n−j+k
· · ·u
′′
n−1
u
′
0
· · ·u
′
n−j−1
.
Now using (11) we get the following expression for
w
′
j
and w
′′
j
w
′
j
= L
k
(M
U
) · C
j
(M
V
) for 1 ≤ j ≤ k,
w
′′
j
= L
k
(M
U
) · C
j
(M
V
) for k + 1 ≤ j < n.
These operations can be done in a parallel hardware
architecture. Specially each coefficient w
i
, w
′
i
and w
′
i
we perform in parallel a scalar product through paral-
lel AND gates, and a binary tree of XOR.
Complexity. Let us evaluate the complexity of this
multiplier. It consists in (2n−1) scalar products done
in parallel:
• n for the coefficients w
j
, j = 0, . . . , n − 1,
• n − 1 for the w
′
j
, with j = 0, . . . , k − 1 and w
′′
j
with j = k + 1, . . . , n − 1.
Since one scalar product requires n AND and (n − 1)
XOR, the overall space complexity of the multiplier is
equal to (2n − 1)n AND and (2n − 1)(n − 1) XOR .
For the time complexity, since the computation of the
coefficients of CMR(W) are done in parallel, the time
complexity is equal to the delay of only one scalar
product. But this delay is equal to T
A
+⌈log
2
(n)⌉T
X
.
6 EXAMPLE
We consider the field F
2
5
= F
2
[X]/(X
5
+ X
2
+ 1).
Let U = u
0
+ u
1
X + u
2
X
2
+ u
3
X
3
+ u
4
X
4
∈ F
2
5
.
The condensed matrix representation of U is given by
the three vectors
U = (u
0
, u
1
, u
2
, u
3
, u
4
, u
5
),
U
′
= (u
′
0
, u
′
1
), U
′′
= (u
′′
3
, u
′′
4
).
where the u
′
i
and u
′′
i
are defined by
u
′
0
= u
0
+ u
3
, u
′
1
= u
1
+ u
4
,
u
′′
3
= u
3
+ u
1
+ u
4
, u
′′
4
= u
4
+ u
2
,
Using the general formula (7) for M
U
we get that
M
U
is as follows
M
U
=
u
0
u
4
u
3
u
2
u
′
1
u
1
u
0
u
4
u
3
u
2
u
2
u
′
1
u
′
0
u
′′
4
u
′′
3
u
3
u
2
u
′
1
u
′
0
u
′′
4
u
4
u
3
u
2
u
′
1
u
′
0
.
Now if U = 1 + X
3
+ X
4
and V = X + X
2
their
condensed matrix representation are
CMR(U) =
U = (1, 0, 0, 1, 1),
U
′
= (0, 1), U
′′
= (0, 1).
CMR(V ) =
V = (0, 1, 1, 0, 0),
V
′
= (0, 1), V
′′
= (1, 1).
Using the vectors U, U
′
, U
′′
we can construct M
U
and
with the vectors V, V
′′
and V
′′
we can construct M
V
M
U
=
1 1 1 0 1
0 1 1 1 0
0 1 0 1 0
1 0 1 0 1
1 1 0 1 0
, M
V
=
0 0 0 1 1
1 0 0 0 1
1 1 0 1 1
0 1 1 0 1
0 0 1 1 0
.
Let W = U V be the product of U and V in F
2
5
.
We compute the condensed matrix representation of
W by multiplying well chosen line of M
U
and well
chosen line of M
V
as described in the previous sec-
tion.
We compute w
0
by multiplying L
0
(M
U
) the first
line of M
U
with C
0
(M
V
) the first column of M
V
w
0
= L
0
(M
U
) · C
0
(M
V
)
= [
1 1 1 0 1
] ·
t
[
0 1 1 0 0
] = 0
For w
i
, i = 1, 2, 3, 4 we have
w
1
= L
1
(M
U
) · C
0
(M
V
) = 0,
w
2
= L
2
(M
U
) · C
0
(M
V
) = 1,
w
3
= L
3
(M
U
) · C
0
(M
V
) = 1,
w
4
= L
4
(M
U
) · C
0
(M
V
) = 1.
For the coefficients w
′
i
we do
w
′
1
= L
2
(M
U
) · C
1
(M
V
) = 1,
w
′
2
= L
2
(M
U
) · C
2
(M
V
) = 1.
And finally for the coefficients w
′′
i
we have
w
′′
3
= L
2
(M
U
) · C
3
(M
V
) = 0,
w
′′
4
= L
2
(M
U
) · C
4
(M
V
) = 0.
We can easily check that the coefficients w
i
, w
′
i
and
w
′′
i
are the correct coefficients of the condensed ma-
trix representation of the product of U and V in F
2
5
.
SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY
258
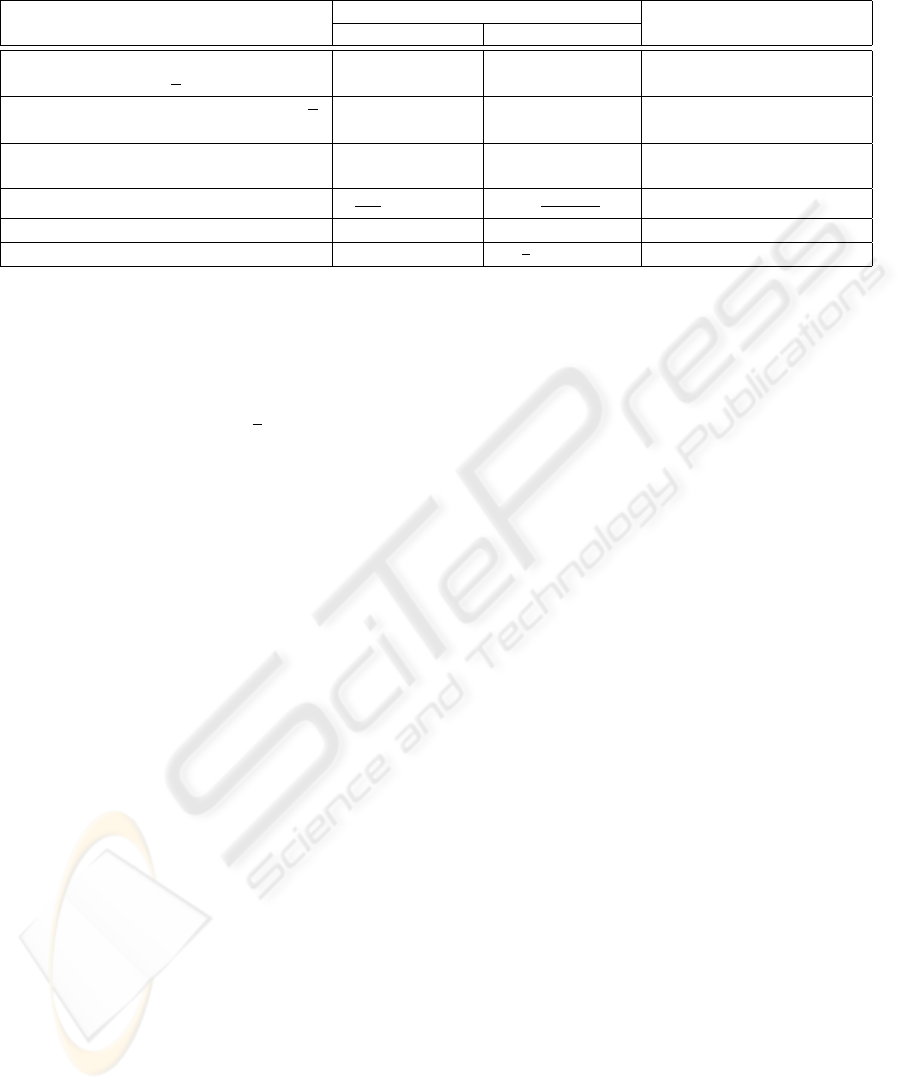
Table 3: Complexity.
Algorithm Space complexity Time complexity
# AND # XOR
CMR for X
n
+ X
k
+ 1 (2n − 1)n (2n − 1)(n − 1) T
A
+ (⌈log
2
(n)⌉)T
X
with 2 ≤ k ≤
n
2
(this paper)
PB for X
n
+ X
k
+ 1 with 2 ≤ k ≤
n
2
n
2
(n
2
− k) T
A
+ (2 + ⌈log
2
(n)⌉)T
X
(Koc and Sunar, 1999)
PB for X
n
+ X + 1 n
2
(n
2
− 1) T
A
+ (1 + ⌈log
2
(n)⌉)T
X
(Koc and Sunar, 1999)
PB for AOP (Chang et al., 2005) (
3n
2
4
+ 2n + 1)
+
3(n+2)
2
4
T
A
+ (1 + ⌈log
2
(n)⌉)T
X
NB of Type I (Wu and Hasan, 1998) n
2
(n
2
− 1) T
A
+ (1 + ⌈log
2
(n)⌉)T
X
NB of type II (Koc and Sunar, 2001) n
2
3
2
(n
2
− n)
T
A
+ (1 + ⌈log
2
(n)⌉)T
X
7 CONCLUSION
We have presented in this paper a new multiplier ar-
chitecture for binary field F
2
n
generated by a trino-
mial X
n
+X
k
+1 with 2 ≤ k ≤
n
2
using a condensed
matrix representation. This multiplier is highly paral-
lelizable.
In Table 3 we give the complexity of our architec-
ture, and also the complexity of different multiplier
architectures proposed in the literature for field F
2
n
.
We see that the use of a condensed matrix repre-
sentation provides a multiplication which is the faster
among all previously proposed multiplier known by
the author. The gain on time complexity for multipli-
cation modulo trinomials X
n
+ X
k
+ 1 with crypto-
graphic size n ∼ 160 is around 20% when k ≥ 2
compared to polynomial basis multiplier and 10%
compared to normal basis multiplier or AOP polyno-
mial bases. But we have to pay a big price for this
improvement : the condensed matrix representation
parallel multiplier has a space complexity which is
roughly two times bigger than classical polynomial
and normal basis multiplier.
REFERENCES
Berlekamp, E. (1982). Bit-serial Reed-Solomon encoder.
IEEE Trans. Information Theory, IT-28:869–874.
Chang, K.-Y., Hong, D., and Cho, H.-S. (2005). Low com-
plexity bit-parallel multiplier for GF(2
m
) defined by
all-one polynomials using redundant representation.
IEEE Trans. Comput., 54(12):1628–1630.
Koc, C. and Sunar, B. (1999). Mastrovito Multiplier for
All Trinomials. IEEE Transaction on Computers,
48(5):522–52.
Koc, C. and Sunar, B. (2001). An Efficient Optimal Normal
Basis Type II Multiplier. IEEE Trans. on Computers,
50:83–87.
Lidl, R. and Niederreiter, H. (1986). Introduction to Finite
Fields and Their Applications. Cambridge Univ Press.
Mastrovito, E. (1991). VLSI architectures for computations
in Galois fields. PhD thesis, Dep.Elec.Eng.,Linkoping
Univ.
Miller, V. (1985). Uses of elliptic curves in cryptography.
Advances in Cryptology, proceeding’s of CRYPTO’85,
Lecture Note in Computer Science 218.
Silverman, J. H. (1999). Fast Multiplication in Finite Fields
GF(2
n
). In Crytographic Hardware and Embedded
Systems - CHES’99, volume 1717 of LNCS, pages
122–134.
Wu, H. and Hasan, M. (1998). Low-Complexity Multipliers
Bit-Parallel for a Class of Finite Fields. IEEE Trans.
Computers, 47:883–887.
PARALLEL MULTIPLICATION IN F2n USING CONDENSED MATRIX REPRESENTATION
259
