
MEASURED MIMO CAPACITY ENHANCEMENT IN CORRELATED
LOS INDOOR CHANNELS VIA OPTIMIZED ANTENNA SETUPS
Andreas Knopp, Mohamed Chouayakh, Robert Schwarz and Berthold Lankl
Department of Electrical and Electronics Engineering, Institute for Communications Engineering,
Munich University of the Federal Armed Forces, 85579 Neubiberg, Germany
Keywords:
MIMO techniques, indoor channel measurements, channel capacity, correlated channels, Line-Of-Sight.
Abstract:
Our premise in this paper is to investigate the available channel capacity of MIMO systems in correlated
transmission channels for various antenna arrangements differing in their suitability in order to construct high -
rank LOS channels. Hence, a measurement campaign with a fast 5×5 - MIMO channelsounder was carried out
in a typical, medium - scale, in - room office scenario giving the opportunity to virtually evaluate the channel
capacities for arbitrary M × N - MIMO systems ({M, N} ≤ 5) by antenna selection and combination. We
use linear antenna arrays and vary their initial antenna spacings and orientations relative to each other which
coincides with LOS channels of varying rank. In the sequel the measured capacities are compared giving an
idea on the usefulness of the high - rank LOS channel construction in the presence of strong reflections. For
our purpose we introduce an appropriate power normalization of the channel transfer matrix to exclude further
effects on the capacity, as for example SNR variations due to varying transmitter - receiver distances, and only
concentrate on the phase angle relations within the matrix. The results show a measurable benefit in channel
capacity when such optimization and normalization is performed, especially for small antenna numbers.
1 INTRODUCTION
Multiple Input - Multiple Output (MIMO) transmis-
sion systems promise high channel capacity gains
and reliability improvements for fixed bandwidth and
transmit power (Telatar, 1995),(Foschini and Gans,
1998). In the context of the system design it is in-
evitable to be able of predicting the accessible chan-
nel capacity. Especially indoor transmission channels
and as a subgroup in-room channels, where transmit-
ter (Tx) as well as receiver (Rx) are located within the
same room, are totally different from common statis-
tical modelling approaches due to their strong Line
- Of - Sight (LOS) signal component in coincidence
with low mobility. In the narrowband case such cor-
related channels have been shown to typically pro-
vide only low MIMO outage capacities, particularly
for small antenna spacings relative to the Tx - Rx
distance (Vucetic and Yuan, 2003), (Molisch, 2005).
Contrarily, theory offers the possibility to enhance
the MIMO capacity of correlated channels by adapted
antenna arrangements that are suitable for construct-
ing high - rank LOS channels, e.g. (Bohagen et al.,
2005). These approaches explore full MIMO capac-
ity for fixed antenna positions as long as there are no
reflected waves impinging at the Rx - two conditions
that are hardly fulfilled in practice. On the one hand it
is impossible to optimize the antenna setups for every
position in the room and on the other hand the LOS
signal never exists without reflections. Nevertheless
we consider the LOS component being carrying most
of the signal power. Therefore optimally chosen an-
tenna setups which nearly can exploit the LOS com-
ponent all over a particular room area should help
to improve the channel’s outage capacity even in the
presence of reflections. This approach will particu-
larly be probed in the sequel. Hence, in section 2 a
channel description is provided and the capacity cal-
culation is described. In section 3 we present our re-
sults from measurements as well as some preliminary
insights derived from simulation. Last, we conclude
the paper in section 4.
2 CHANNEL MODEL AND
CAPACITY CALCULATION
General presumptions on the channel: In the con-
text of MIMO applications and their capacity the in-
187
Knopp A., Chouayakh M., Schwarz R. and Lankl B. (2006).
MEASURED MIMO CAPACITY ENHANCEMENT IN CORRELATED LOS INDOOR CHANNELS VIA OPTIMIZED ANTENNA SETUPS.
In Proceedings of the International Conference on Wireless Information Networks and Systems, pages 187-193
Copyright
c
SciTePress

door WLAN channel is commonly statistically mod-
elled, where the modelling approaches concentrate on
the NLOS transmission paths forming numerous and
variously reflected waves (”rich scattering”). To ful-
fill these assumptions the LOS component must be
distinctly attenuated by shadowing effects or when as-
suming high reflection factors ξ
2
≈ 1 the path lengths
of the reflected waves must be in the range of the LOS
path length. In this case the propagation loss of direct
and reflected signal components range in the same or-
der of magnitude and hence the reflection’s impact
rises. Usually those assumptions are less valid for in
- room scenarios than for outdoor transmission with
large distances between Tx and Rx. Therefore a sim-
ilar modelling strategy is regularly performed in mo-
bile communications. When in addition narrow trans-
mission bandwidths are presumed the channel can be
treated flat and information is provided only on the
magnitude level distribution which especially in the
case of high mobility can be modelled by a Rayleigh
process (Paetzold, 2002). In this case the entries of
the channel transfer matrix are assumed to be uncor-
related, zero mean, i.i.d. complex Gaussian random
variables, a case which describes a convenient trans-
mission channel for MIMO applications as the ex-
pected value of its capacity is high (Telatar, 1995) as
long as the receive signal correlation is kept low. Ac-
cording to (Jakes, 1974) the latter condition can be
achieved by antenna spacings of at least about half -
wavelength (λ/2) what therefore has become a com-
mon design issue for MIMO antenna arrays. When
the direct LOS signal component gets present this fact
can be incorporated leading to the well known Rice
propagation model (Paetzold, 2002). This statistical
approach is widely used when discussing early indoor
transmission systems and it is included in the popu-
lar, cluster based channel model introduced by Saleh
(Saleh and Valenzuela, 1987).
Contrarily, in the case of the in - room propagation
scenario discussed in the sequel a dominant LOS sig-
nal component that carries most of the energy is al-
ways present which in the consequence leads to cor-
related signals at the receiver inputs. Of course also in
indoor scenarios the LOS signal component ist some-
times obstructed and therefore diffracted by objects
but it is known from the theory of diffraction that no
significant losses arise as long as the obstructing ob-
stacle’s size stays below the first Fresnel zone’s di-
mension. For a typical WLAN center frequency of 2.4
GHz and distances of 2 m and 3 m between the obsta-
cle and the Tx and Rx, respectively, the size of the first
Fresnel zone is about 80 cm in diameter which is large
compared to typical furniture or persons. Besides, one
set of antennas (Tx or Rx) is typically mounted at the
ceiling which distinctly reduces the risk of obstruc-
tion. In these scenarios the simple approach of a λ/2
antenna spacing is no longer sufficient as it theoret-
ically can not exploit the maximum MIMO capacity
with respect to LOS. By geometrically optimizing the
antennas’ positions and spacings at Tx as well as Rx
resulting in proper phase angle relations among the
entries of the channel transfer matrix, it is possible to
make accessible the maximum MIMO capacity even
in the case of correlated channels. Coinciding it is
inevitable that the LOS signal component never ex-
ists without reflections which can hardly be included
in any strategy of constructing high - rank channel
transfer matrices. Obviously this effect gets more em-
inent when the power contributed by reflections rises
as it is the case for declining room dimensions. Be-
fore we answer the question to what extent the high
- rank LOS channel construction enhances the capac-
ity in such real - world scenarios the theoretic back-
ground in terms of channel modelling and capacity
calculation is summarized.
Capacity calculation: Contingent upon the consid-
ered transmission bandwidth our measurements cover
the case of nearly frequency flat channels. Neverthe-
less, a frequency selective channel model should be
assumed because it also includes the frequency flat
channel as a special case and it is necessary for our
way of evaluating the measured results as it will be ex-
plained in the sequel. According to our presumptions
mentioned above we consider the following, widely
deterministic description of the MIMO transmission
channel. For a single input - single output (SISO) fre-
quency selective, deterministic transmission channel
the equivalent baseband channel transfer function for
the time invariant case is given by
H(f) =
K−1
X
k=0
a
k
e
−j2πf τ
k
=
K−1
X
k=0
a
k
e
−j2π
L
k
λ
, (1)
where the sum is evaluated over the K different trans-
mission paths consisting of K − 1 reflected signal
parts and the LOS signal component is incorporated
by the index k = 0. The complex amplitude factor
a
k
includes the phase information φ, the path - loss
as well as the power - loss due to the reflection fac-
tor ξ
2
, i.e. a
k
=
ξλ
4π L
k
e
jφ
. The time τ
k
denotes the
signal part’s delay for the particular transmission path
which is clearly linked to its path length L
k
by the
speed of light c
0
, i.e. τ
k
= L
k
/c
0
. The right part of
the equation additionally introduces H(f ) depending
on the wavelength λ. For a non - mobile scenario a
k
and τ
k
are mainly constituted by the location’s geom-
etry, i.e. primarily by the Tx’s and Rx’s positioning
within the room as well as their arrangement in rela-
tion to the main reflection layers like walls, bottom,
ceiling or large scale objects. With increasing mobil-
ity it is more and more appropriate for the channel
to be modelled by some statistical process. In the ob-
served scenarios described in this paper the amount of
WINSYS 2006 - INTERNATIONAL CONFERENCE ON WIRELESS INFORMATION NETWORKS AND SYSTEMS
188

mobility is kept low and therefore no statistical mod-
elling over time is performed.
Applying equation (1) to the MIMO case, for a time
invariant frequency selective M × N - MIMO sys-
tem consisting of N transmit and M receive antennas
the vector of receive signals y(t) ∈ C
M×1
is calcu-
lated by an inverse Fourier transform of the spectrum
of the transmit signal vector X(f) ∈ C
N×1
multi-
plied by the frequency selective channel transfer ma-
trix H(f ) ∈ C
M×N
, i.e.
Y (f ) = H(f) X(f ) + Υ(f), (2)
where Υ(f) ∈ C
M×1
denotes the spectral vector of
the additive noise η(t). The noise is assumed to be
zero-mean complex Gaussian with covariance matrix
R
η
= E[ηη
H
] = σ
2
η
I
M
, where I
M
∈ C
M×M
de-
notes the identity matrix and σ
2
η
is the noise power
at each receive antenna. Here each entry H
mn
(f) in
H(f) has the structure of equation (1) whereas the
values K and hence, a
k
and τ
k
differ.
According to (Telatar, 1995) and (Foschini and Gans,
1998) when uncorrelated transmit signals are pre-
sumed the time invariant channel capacity for a fre-
quency selective MIMO - channel in the absence of
channel knowledge at the transmitter is calculated
from
C =
B
log
2
det
I
M
+
σ
2
x
σ
2
η
H(f)H
H
(f) df, (3)
where B denotes the transmission bandwidth, I
M
∈
C
M×M
is the identity matrix, σ
2
x
denotes the mean
transmit power that is allocated to each transmit an-
tenna. Furthermore (.)
H
abbreviates the complex con-
jugate transpose. When the overall bandwidth is par-
titioned into sufficiently narrow, say S, segments each
segment can be treated frequency flat and the integral
of equation (3) reduces to a sum over the segments’
capacity contributions, i.e.
C =
B
S
S
s=1
log
2
det
I
M
+
σ
2
x
σ
2
η
H[f
s
]H
H
[f
s
] . (4)
Equation (4) is used for the capacity calculation from
measured data samples in section 3. From equations
(3) and (4) it can be observed that the capacity is op-
timized by finding the optimal matrix entries in the
channel transfer matrix H(f ) dependent upon the fre-
quency f. When only a LOS signal component is
present this can be resolved by geometrically optimiz-
ing the antennas’ position such that a high - rank chan-
nel transfer matrix is obtained. Several early sugges-
tions from different authors, e.g. (Driessen and Fos-
chini, 1999), were made for the construction of these
channels but all of them suffer from the drawback that
due to mathematical restrictions they are limited to
only a small number of antennas. Furthermore the re-
sulting geometric setups are often improper for prac-
tical applications as in the consequence the antennas
have to be positioned far from each other all over the
room. A recent and most general solution which over-
comes the drawback of limited antenna numbers can
be found in (Bohagen et al., 2005) where the authors
present a strategy for the design of linear antenna ar-
rays which under weak presumptions leads to a chan-
nel transfer matrix close to full - rank.
Additionally a very simple example which illustrates
a possibility to optimize the channel capacity even in
deterministic correlated MIMO channels in the case
of a flat fading for a fixed location of Tx and Rx can
be found in (Knopp et al., 2005). Of course in prac-
tice such optimization would have to be performed
for every possible location what is far from realizabil-
ity. Despite this fact the simple example and further
analysis that have been performed in advance of our
measurements, e.g. the deviation of the pure LOS
capacity across a room of particular size for various
antenna spacings, suggest that it is reasonable to gen-
erally enlarge the antenna spacings in order to better
exploit the strong LOS signal component for possi-
bly large areas of a room without taking into account
reflections. The arising question to what extent the
antenna setup’s simplified optimization for LOS via
enlarged but fixed antenna spacings all over the room
even in conjunction with reflections stays still prof-
itable is discussed in section 3.
3 RESULTS
3.1 Scenario Description and
Method of Measurement
For the channel measurements we used a 5×5 MIMO
channelsounder with a bandwidth of 80 MHz at a
carrier frequency of 2.45 GHz endowed with λ/2
dipole antenna arrays positioned as equidistantly -
spaced uniform linear arrays (ULAs). The maxi-
mum bandwidth ranges some factor above the typ-
ical bandwidths proposed for current and future in-
door applications and hence, achieves a higher time
resolution. The channel information was collected
by sequentially deriving the entries of the channel
transfer matrix, i.e. by collecting the complex base-
band channel impulse responses (CIRs) and channel
transfer functions (CTFs). A Perfect Squares - Mini-
mum Phase (PS - MP) CAZAC sequence (Linde and
Roehrs, 1993) was used as pilot signal, a discrete
sequence with a frequency flat power spectrum and
therefore a perfectly zero autocorrelation for differ-
ent time instances. We used 196 pilot symbols and
due to our sampling rate of 100 MHz we achieved
a frequency resolution of 510 kHz (196 · 510 kHz
= 100 MHz), but for the capacity evaluation we re-
duced the considered bandwidth off line to 80 MHz
MEASURED MIMO CAPACITY ENHANCEMENT IN CORRELATED LOS INDOOR CHANNELS VIA OPTIMIZED
ANTENNA SETUPS
189
by digital filtering. The measurement of one complete
channel matrix consisting of 25 entries took about
160 µs. This measurement time is short enough by
far to consider the channel invariant during that time,
especially in the chosen scenarios with low mobility
and it is much faster than even a single SISO network
- analyser measurement which typically takes around
100 ms. A further advantage of the system is the fact
that after measuring the 25 CIRs we are able to arbi-
trarily combine them in off - line mode and virtually
built up different MIMO systems by antenna selection
from the measured data, in fact
5
M
5
N
combinations
are possible for an M × N MIMO system.
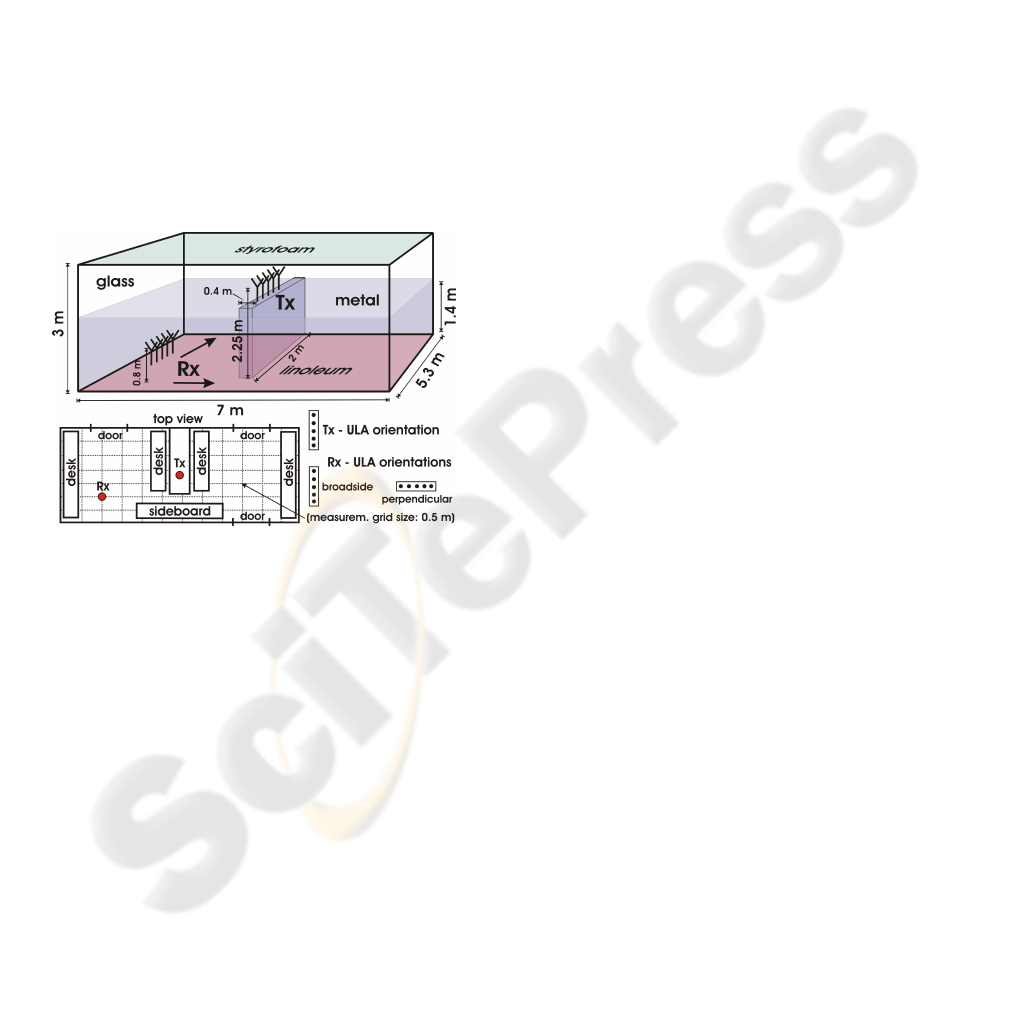
The measurements were taken within a modern office
building constructed from steel and glass. We chose
a typical medium - scale office or laboratory scenario
which is depicted in detail in figure 1 providing all
necessary information on the materials, dimensions
and arrangements of the walls and the most impor-
tant furniture. The room was equipped by typical of-
Figure 1: Schematics of the measured location.
fice working desks, i.e. wooden desks and chairs with
metal legs. Additionally a metal bar was placed in the
center of the room dealing as a divider. The Tx was
arranged on top of that divider at height 2.25 m what
supposes that in the context of in - room scenarios
the Tx might reasonably be placed near the ceiling to
guarantee a LOS link for every receiver position. The
Tx position was kept fixed while the Rx was moved at
typical working desk hight in two dimensions across
the room along a grid. During one complete grid mea-
surement the relative positions of the Tx and Rx an-
tenna array were not changed and either broadside or
perpendicular (see fig. 1). The mobility was kept low
and therefore the statistical analysis of the measured
data was performed in the spatial domain treating the
Rx position as a random variable. The statistic was
expanded by an additional evaluation of the 196 fre-
quency segments of bandwidth 510 kHz which our
sampled transfer function was partitioned into. We as-
sumed every frequency segment being a realization of
a possible narrow band transmission channel out of 80
MHz / 510 kHz = 156 possible transmission channels
around the carrier of 2.45 GHz. From equation (1) it
becomes obvious that the relation L
k
/λ is the key pa-
rameter for the CTF’s phase angle as well as its path
- loss. Changing the Tx - Rx distances the value L
k
is changed resulting in a different CTF. Changing the
carrier frequency the wavelength λ is changed what
also alters the CTF. Interpreting the variation of L
k
/λ
due to the change of λ as if λ was kept fixed and L
k
was altered instead, the statistical evaluation of dif-
ferent frequency segments which are placed close to
each other around the carrier can be interpreted as vir-
tually moving the Rx within a small area. This strat-
egy provides the possibility to enlarge our spatial sta-
tistics.
3.2 Mimo SNR Definition and
Capacity Normalization
A crucial aspect when evaluating measured channel
transfer functions in terms of the channel capacity is
the definition of the signal to noise ratio in equation
(3). Generally, we suggest a definition that best rep-
resents the physical reality of transmission systems
with respect to their degrees of freedom for the user.
Those are mainly the transmit power per transmit an-
tenna σ
2
x
and the noise power per receive antenna σ
2
η
as the latter includes the receiver noise figure which
depends on the chosen hardware. Of course with that
definition the ratio σ
2
x
/σ
2
η
does not meet the com-
monly used SNR definition ρ which describes the re-
ceive signal to noise ratio at the receiver input, but ρ
clearly emanates from σ
2
x
/σ
2
η
if it is multiplied by the
channel’s path loss ζ
2
, i.e. ρ = σ
2
x
/σ
2
η
· ζ
2
. In our
definition ζ
2
is completely incorporated in the chan-
nel transfer matrix which causes ρ at the receiver in-
put being dependent upon the distance between Tx
and Rx as well as the number and power of imping-
ing waves. This approach does best represent phys-
ical reality as it focusses on the true capacity avail-
able in practice including all the relevant effects. To
give an example: if the commonly investigated Non
- LOS Rayleigh flat fading channel for a given value
of ρ (which again denotes the resulting SNR at the re-
ceiver input) is considered, the capacity will be com-
paratively close to its maximum for that ρ. If now
a strong LOS signal component is brought into the
scene the value of ρ will be distinctly higher what
rises the true channel capacity. If the rank of the
channel transfer matrix for certain geometric antenna
arrangements is observed, it will be close to rank = 1
for the LOS case and close to full - rank without the
LOS. Nevertheless, if one concludes from the obser-
vation of the channels’ ranks that the one with LOS
WINSYS 2006 - INTERNATIONAL CONFERENCE ON WIRELESS INFORMATION NETWORKS AND SYSTEMS
190
present is worse for MIMO applications, this conclu-
sion in most cases will be totally wrong as the SNR
gain is ignored. The risk of such misinterpretation es-
pecially rises if the comparison of the two channels
is performed by simply substituting ρ for σ
2
x
/σ
2
η
and
in addition normalizing the channel transfer matrix by
an appropriate matrix norm to unit power for compen-
sation, i.e. eliminating the path loss from the channel.
If now the two power - normalized channels are com-
pared for the same value of ρ, the Non - LOS chan-
nel will clearly outperform the LOS channel, a result
which is far from the truth in most cases. Hence, we
propose to avoid any normalization to evaluate dif-
ferent channels with respect to their effective channel
capacity.
Nevertheless, if one’s interest focusses on certain ef-
fects and their influence on the capacity it might be
reasonable to eliminate all the further effects that af-
fect the capacity besides. In this paper we concretely
investigate the antenna arrangement’s impact on the
channel capacity what rather means that we want to
find out how different antenna spacings can influence
the channel matrix’ rank in the presence of reflec-
tions. We perform a spatial statistics what coincides
with varying Tx - Rx distances. As we do not want to
take into account the variation of ρ due to those dis-
tance changes we therefore replace σ
2
x
/σ
2
η
in equa-
tion (3) by ρ and keep its value fixed (in the sequel
it is set to ρ = 30 dB), while we eliminate the path
loss from the channel transfer matrix by normalizing
it to unit power using the Frobenius matrix norm, i.e.
||H||
2
F
= 1. This norm simply sums up the matrix
entries’ power and normalizes by that sum. The strat-
egy is appropriate for our investigations but the reader
should be aware of the given presumptions when in-
terpreting the results. To give a physical interpreta-
tion, the used normalization is equivalent to perma-
nently adjusting the Tx power in order to keep the Rx
input power and therefore ρ fixed independently from
the channel.
3.3 Evaluation of the Results
Preliminary simulations: To develop an idea of the
reflections’ impact on the outage capacity (OC)
1
be-
fore presenting our measured results we provide re-
sults from simulation. We simulatively obtained ca-
pacity cumulative distribution functions (CDFs) for a
room with identic dimensions as our measurement lo-
cation while considering the direct (LOS) signal com-
ponent as well as the reflections from all the surround-
ing walls, the bottom and the ceiling. In the simpli-
fied simulation we included single, double, triple and
1
the x % outage capacity describes the capacity value
which is NOT exceeded with a probability of x % (Vucetic
and Yuan, 2003)
quadruple reflections and calculated them by means
from geometric optics using a spherical wave model
but ignored further effects like diffraction, scattering
and transmission through objects. The Tx was placed
in the center of the room and the Rx was moved, both
at a height of 1.5 m. The reflection factor was set to
0.3 what corresponds to an amplitude - loss of 10.5
dB, which describes a typical but comparatively high
reflection factor for indoor materials what in the con-
sequence slightly overestimates the reflection’s power
marking a worse case than practically expected. Sim-
ilar to our measurements and in accordance to the
description of subsection 3.1 the simulation was per-
formed over a bandwidth of 80 MHz formed by nar-
rowband frequency segments of 500 kHz and the re-
sults were statistically evaluated over a spatial grid as
well as over those frequency segments. The capacities
were calculated according to equation (4). Besides
the normalization of the channel transfer matrix we
furthermore normalized the capacity by min{M, N}
which is equivalent to the maximum linear capacity
increase of an M × N - MIMO system. This normal-
ization leads to capacities which are approximately
independent from the number of antennas and there-
fore also eases comparability as the capacity CDFs lie
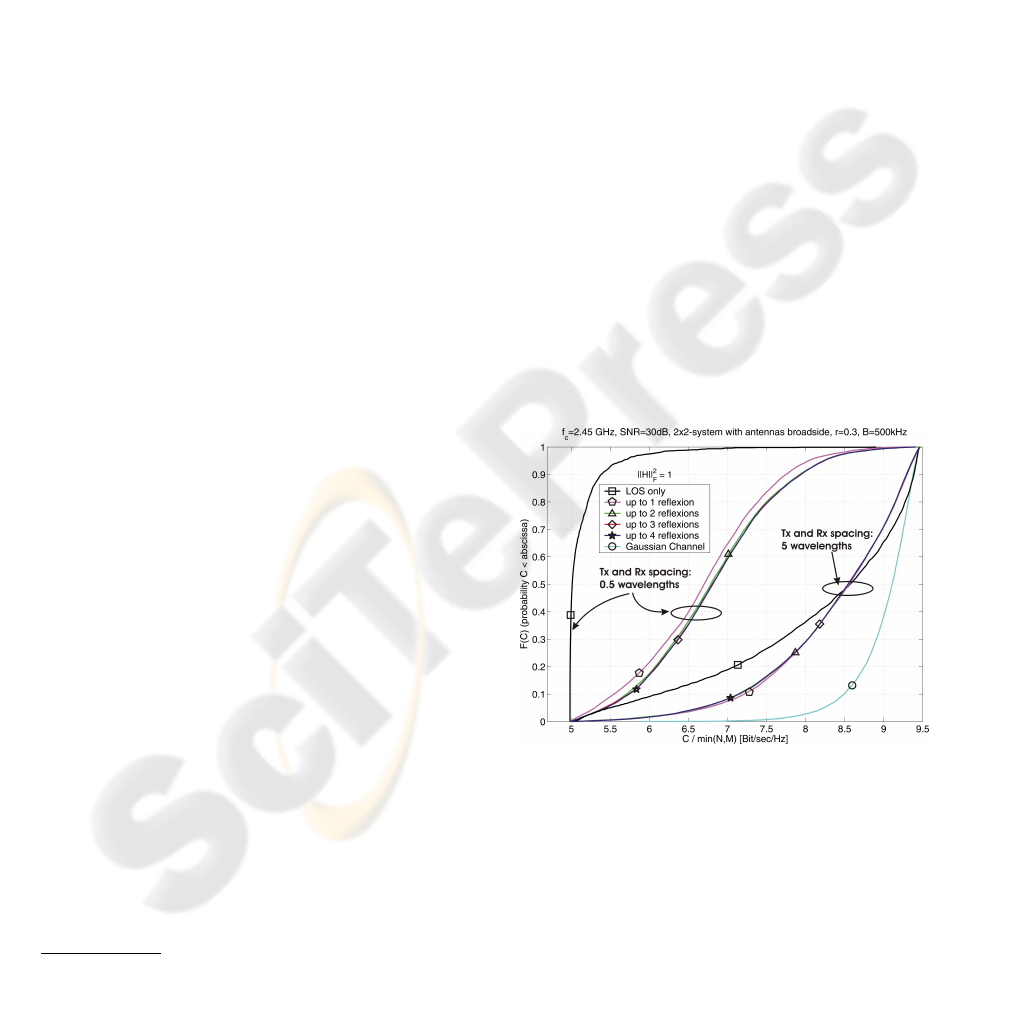
within similar ranges of magnitude. The results for a
2 × 2 - MIMO system with different antenna spacings
(equally chosen at Tx and Rx) are depicted in figure
2. For both antenna spacings 5 curves can be observed
Figure 2: Simulated C-CDFs for different antenna spacings.
differing in the considered number of reflections. The
legend entry ”up to 2 reflections” for example denotes
the case of considering the LOS signal part and all
reflected waves which were reflected twice at maxi-
mum. For the usually chosen λ/2 spacing the CDF
considering only the LOS signal part clearly indicates
a very low capacity with low spatial variations what
can be seen from the steepness of the curve. This can
be understood from the fact that the channel trans-
MEASURED MIMO CAPACITY ENHANCEMENT IN CORRELATED LOS INDOOR CHANNELS VIA OPTIMIZED
ANTENNA SETUPS
191
fer matrix is close to rank = 1 for that small antenna
spacings nearly all over the room. Obviously when
reflections are included the capacity increases, the 50
% OC for example is increased by about 35 % com-
pared to its minimum for the 2×2 - MIMO system but
the 10 % OC only slightly increases by about 15 %.
Obviously the reflections help to increase the OCs by
enhancing the channel transfer matrix’ rank but com-
pared to the case of a Rayleigh fading channel of iden-
tical power the capacity stays still low.
Contrarily, when the antenna spacing is enlarged what
according to the example presented in the previous
section coincides with enhanced utilization of the
LOS component in terms of MIMO the 10 % OC for
the pure LOS is increased already by over 20 % and
the 50 % OC is even increased by about 72 %. Con-
sidering the reflections in addition the 10 % OC is
further increased by 18 % while the 50 % value stays
unchanged compared to the pure LOS case. From
that OC onwards the reflections no longer increase
the MIMO gain, contrarily from about the 50 % OC
up they even reduce it. This supports the idea that in
optimally configured systems with respect to LOS the
reflections disturb the well adapted phase angle rela-
tions within the transfer matrix (see (Bohagen et al.,
2005), (Knopp et al., 2005)) and therefore reduce the
capacity although in the simulation only a negligi-
ble reduction can be observed. The low steepness
of the pure LOS CDF in the large antenna spacing
case shows the second problem of the optimization
approach: any optimized antenna spacing only holds
for a certain spatial region and can even correspond to
the worst case outside that region. Therefore the spa-
tial variation of the capacity for a fixed antenna spac-
ing is high. Last, it is observed from the figure that
in the low capacity case with a LOS channel transfer
matrix close to rank = 1 its rank is already distinctly
increased by only considering single reflections and
for the case of double reflections a further capacity
increase can be observed. If the LOS signal part is ex-
ploited well the reflections’ influences on the capacity
reduces meaning the better the LOS is exploited the
more the capacity seems to be statistically dominated
by LOS. Generally it appears to be sufficient in terms
of the capacity if triple and quadruple reflections are
neglected as their weak power contributions can not
significantly change the capacity CDFs.
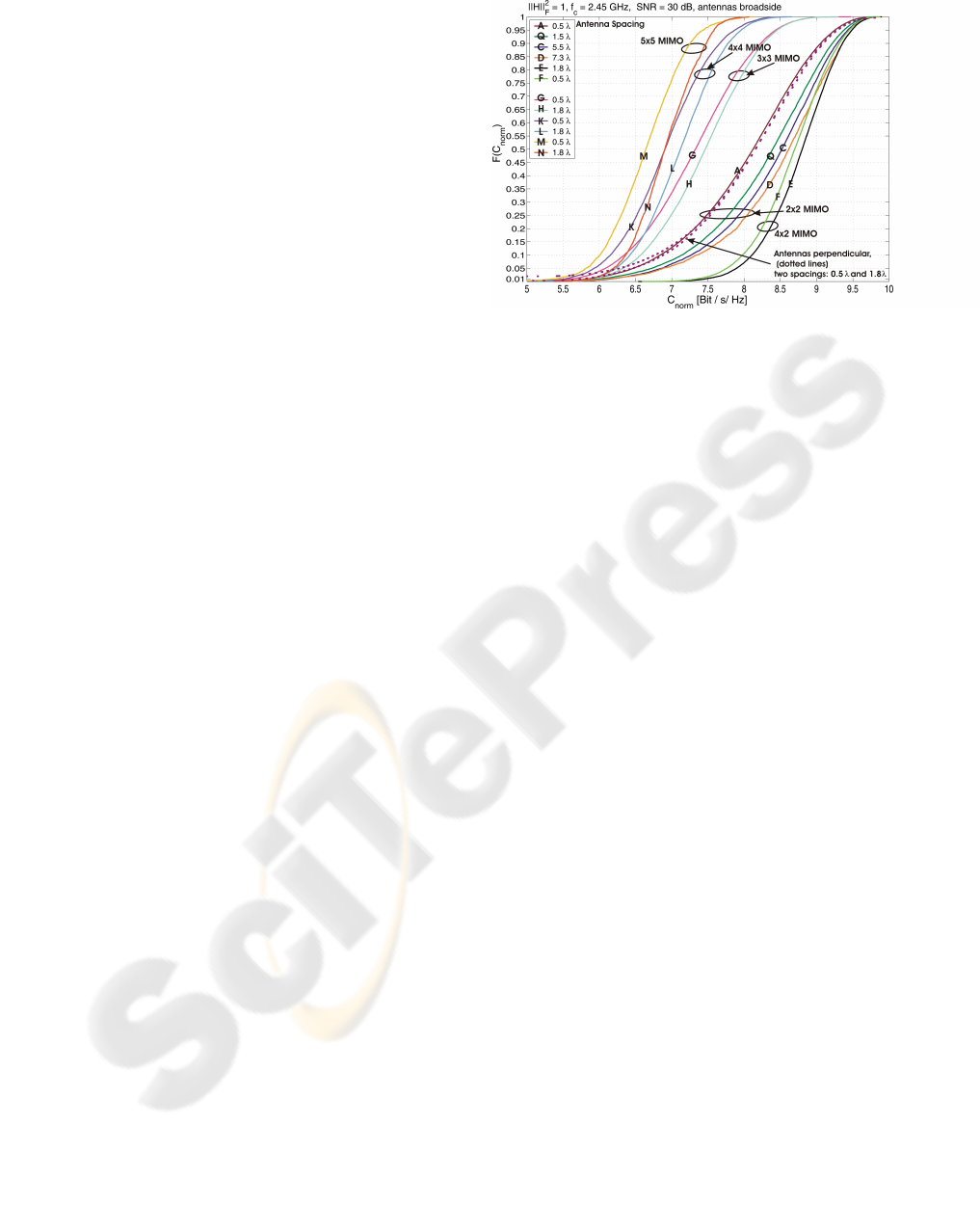
Measurements: Taking a look at the correspond-
ing capacity CDFs obtained from measured data the
basic results from the preliminary, simplified simula-
tions are widely confirmed. It must be outlined in ad-
vance that the particular results (especially the mea-
sured values and numbers) are only valid for the cho-
sen antenna spacings which were not particularly op-
timized to maximize the capacity all over the partic-
ular environment. We just used an arbitrary spacing
Figure 3: Measured C-CDFs for various settings.
larger than half - wavelength which was known to de-
liver local capacity maxima in terms of LOS (Knopp
et al., 2005). We not especially tried to find the dis-
tinctly best choice with the most capacity maxima for
the range Tx - Rx distances in the investigated room
as we hold the opinion that such strategy is far from
practice due to its complexity. So it is still possible
to discover antenna spacings which even outperform
and further stress the results presented next.
Firstly looking at the curves for the narrowband 2 × 2
- MIMO system it can be observed from figure 3 that
for larger antenna spacings the 10 % OC for instance
can be increased up to 10 %. In the contrary to the
simulation for the 50 % OC the percentage increase is
not even higher but slightly lower. On the other hand
even in the λ/2 antenna spacing case which is badly
conditioned for LOS the 10 % OC already reaches a
value about 20 % above the simulation. This supports
the assumption of the simplified simulation model be-
ing not thoroughly sufficient for capacity simulations
as the receive power contributed by reflected and scat-
tered waves seems to be higher than the model ex-
pects, say the scattering is somewhat richer than in
the simulation at least in the medium - scale office
scenario under investigation due to its well reflect-
ing materials. This fact principally has to be regarded
positive for the MIMO channel capacity as the impact
of the LOS - exploitation decreases. Taking a look
at the larger antenna spacings the curves are steeper
in practice than for the larger antenna spacing in the
simulation what states that in the case of nearly opti-
mum antenna spacings with respect to LOS the reflec-
tions disturb the phase relations in the channel trans-
fer matrix and reduce the matrix rank as it already
was expected by theory. Hence, for the current sce-
nario the optimization for LOS by choosing larger an-
tenna spacings still enhances the OC whereas the ca-
pacity gain of about 10 % is comparatively low. If
WINSYS 2006 - INTERNATIONAL CONFERENCE ON WIRELESS INFORMATION NETWORKS AND SYSTEMS
192

beyond the spacing enlargement the number of an-
tennas at Rx and Tx is increased the normalized ca-
pacity gain is still observable but slightly decreases
compared to the case of less antennas. The reason is
found from the fact that the higher the antenna num-
ber the less the simplified approach of larger, equally
chosen antenna spacings fits the optimal configuration
for large areas of the room. So the curves in general
shift closer to the minimum capacity whereas it must
be considered that the real capacity without normal-
ization still gets higher if the number of antennas is
increased
2
. A further result which we obtain from the
curves is the normalized OC increasing for asymmet-
ric MIMO systems with a higher number of receive
antennas as can be seen from the figure. This effect
comes from the enhanced receive diversity which not
only increases the receive power but also reduces the
capacity’s variation as the correlation of the receive
signals is reduced. The curve steepness generally in-
creases for higher number of antennas showing re-
duced capacity variations. A last modification is in-
troduced by changing the antenna arrays’ positioning
towards each other from broadside to perpendicular.
As it was shown in (Knopp et al., 2005) this con-
figuration can hardly exploit the LOS component and
therefore the LOS capacity part stays close to its min-
imum. This configuration is even worse than λ/2 an-
tenna spacing and it is nearly completely independent
from the antenna spacing. This result is widely con-
firmed by the measurements as the spacing enlarge-
ment hardly provides a capacity improvement. Here
again the antenna setup’s important impact is con-
firmed. To shortly summarize the results: as a rule of
thumb the measurements suggest to use antenna spac-
ings of a few wavelengths
3
and choose an asymmetric
MIMO system with a higher number of Rx antennas
than Tx antennas.
4 CONCLUSION
In this paper we showed by measurements that the an-
tenna setup’s adjustment at Rx and Tx in order to con-
struct higher - rank LOS channels might be beneficial
in practice. For the sake of simplicity and practical
realizability we only worked with linear antenna ar-
rays and chose a simplified optimization approach of
changing the antenna spacings and the arrays’ initial
orientation relative to each other and we kept those
parameters fixed for the measurements all over the
room being aware that this proceeding is far from re-
ally optimizing the antenna’s position for every mea-
surement as proposed for example by (Bohagen et al.,
2
remember that our curves in reality have to be multi-
plied by min{M, N}
3
The concrete value is dependent mainly on the dimen-
sion of the room
2005). Despite such simplification we clearly could
enhance the channel’s outage capacity even though
we had to cope with strong reflections and scatter-
ing effects disturbing the LOS signal part. Hence,
we conclude that optimizing indoor MIMO systems
by measures of low complexity for its powerful LOS
signal component already is an appropriate procedure
to enhance the available channel capacity of those cor-
related transmission channels. We furthermore expect
the enhancing effect being even rising with increasing
room dimensions as the reflected waves’ power con-
tribution decreases.
REFERENCES
Bohagen, F., Orten, P., and Oien, G. (2005). Construction
and analysis of high-rank LINE-OF-SIGHT MIMO
channels. In Wireless Communications and Network-
ing Conference, pp. 91-100.
Driessen, P. and Foschini, G. (February 1999). On the
capacity formula for multiple input-multiple output
wireless channels: A geometric interpretation. In
IEEE Transactions on Communications, vol. 47, No.
2, pp. 173-176.
Foschini, G. and Gans, M. (1998). On the limits of wire-
less comunications in a fading environment when us-
ing multiple antennas. In Wireless Personal Commu-
nication, vol. 6, pp. 311-335.
Jakes, W. (1974). Microwave Mobile Communications.
John Wiley & Sons.
Knopp, A., Chouayakh, M., and Lankl, B. (2005). Ca-
pacity optimization and modelling of frequency se-
lective WLAN indoor MIMO channels based on mea-
sured data. In Proceedings of the Third IEEE SSD 05,
Tunisia.
Linde, L. and Roehrs, U. (June 1993). On a class of
polyphase cazac sequences and their application in HF
channel sounding. In The Transactions of the Institute
of Electrical Engineers, pp. 110-123.
Molisch, A. (2005). Wireless Communications. John Wiley
& Sons.
Paetzold, M. (2002). Mobile Fading Channels. John Wiley
& Sons.
Saleh, A. and Valenzuela, R. (1987). A statistical model
for indoor multipath propagation. In IEEE J. Select.
Areas Commun., vol. 5, pp. 128-137.
Telatar, E. (1995). Capacity of multi-antenna gaussian
channels. In AT&T-Bell Technical Memorandum.
Vucetic, B. and Yuan, J. (2003). Space-Time Coding. John
Wiley & Sons.
MEASURED MIMO CAPACITY ENHANCEMENT IN CORRELATED LOS INDOOR CHANNELS VIA OPTIMIZED
ANTENNA SETUPS
193
