FAST CONVERSION OF H.264/AVC INTEGER TRANSFORM

COEFFICIENTS INTO DCT COEFFICIENTS

R. Marques

, V. Silva

1,2

, S. Faria

1,3

, A. Navarro

1,4

, P. Assuncao

1,3

Instituto de Telecomunicações,

Universidade de Coimbra - DEEC, 3030-290 Coimbra, Portugal

Instituto Politécnico de Leiria- ESTG , Apt 4163, 2411-901 Leiria, Portugal

Universidade de Aveiro – DET, 3810-193 Aveiro, Portugal

Keywords: Transform conversion, video transcoding.

Abstract: In this paper we propose a fast method to convert H.264/AVC 4x4 Integer Transform (IT) to standard

Discrete Cosine Transform (DCT for video transcoding applications. We derive the transcoding matrix for

converting, simultaneously, in the transform domain, four IT 4x4 blocks into one 88× DCT block of

coefficients. By exploiting the symmetry properties of the matrix, we show that the proposed conversion

method requires fewer operations than its equivalent in the pixel domain. An integer matrix approximation

is also proposed. The experimental results show that a negligible error is introduced, while the

computational complexity can be significantly reduced.

1 INTRODUCTION

The H.264 is a new video coding standard, recently

approved by ITU-T and ISO/IEC as International

Standard. When compared to earlier video coding

standards like H.263, the H.264 video coding tools

can provide enhanced compression efficiency.

Experimental results show that about 50% of the

bitrate can be saved by using H.264 (Sullivan et al.

2004). Given this coding efficiency, H.264 has been

adopted by various international consortiums like

the Korean Digital Multimedia Broadcasting

(DMB), the European Digital Video Broadcasting

(DVB) and the 3rd Generation Partnership Project

(3GPP) as the standard video codec, and is expected

to be extended to other areas of application, such as,

the Blu-ray Disc (BD).

Whenever a new standard is adopted, this

always gives rise to interoperability problems with

legacy systems. In the case of H.264,

interoperability with MEPG-2 systems is of

particular importance. In general, this is achieved

through video transcoding methods (

Chuang et al.

2005). However, there are significant differences

between the H.264 and other video coding standards,

which difficult the transcoding process, e.g., while

the common video codecs use the

88× Discrete

Cosine Transform (DCT) to reduce spatial

correlation, H.264 uses either

44×

88×

Integer

Transforms (IT). The latter is only used in Frext

profiles (Sullivan et al. 2004).

This paper addresses the problem of converting

H.264/AVC

IT to standard DCT coefficients

for video transcoding applications. We derive the

conversion matrix in the transform domain and

along with a fast algorithm to reduce the number of

operations. Then, we introduce an integer matrix

approximation to increase computing performance

using fixed-point arithmetic.

The organization of this paper is as follows. In

section 2, we describe the proposed transform

domain IT-to-DCT conversion. In sections 3 and 4

the fast conversion algorithm and its integer

approximation are, respectively, described. The

experimental results are presented in section 5 and,

finally, in section 6 the main conclusions are

reported.

2 IT-TO-DCT CONVERSION

The complete (two steps) conversion IT-to-DCT is

shown in

Figure 1. The input is comprised of four

IT blocks,

1234

,,,XXXX. The inverse IT is

Marques R., Silva V., Faria S., Navarro A. and Assuncao P. (2006).

FAST CONVERSION OF H.264/AVC INTEGER TRANSFORM COEFFICIENTS INTO DCT COEFFICIENTS.

In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 5-8

DOI: 10.5220/0001572500050008

 SciTePress

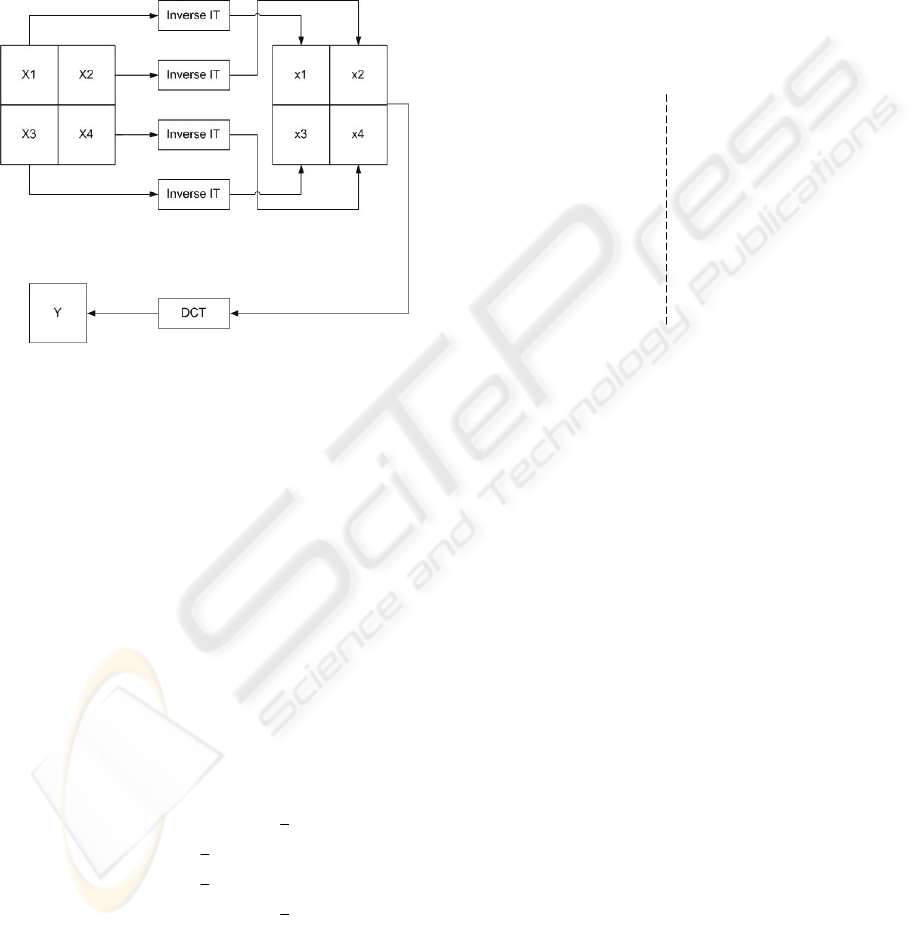
applied to each block in order to obtain the pixel

domain blocks,

1234

,,,xxxx. Then, the four pixel

domain blocks are combined to form a single

block x to which the DCT is applied, such that an

88× block of transform coefficients Y is obtained.

However, a full transform domain conversion (one

step approach) is more efficient because complete

decoding up to the pixel domain is not required.

Figure 1: Pixel domain IT-to-DCT conversion.

The proposed transform domain IT-to-DCT

conversion is based on simple algebraic matrix

relationships (Xin et al. 2004). It is directly applied

to an

88× block X comprised of four

blocks,

,,,

1234

XX X X

, to produce the corresponding

88× DCT block, Y. The conversion is given by the

following operation,

=××YSXS

, (1)

where

S is the transcoding matrix. In order to

derive

S , we have to consider the inverse IT of

blocks,

,,,

1234

XX X X

, given by

,1 4

i=≤≤xJXJ

, (2)

where J is the following matrix (Malvar et al. 2003),

111

⎛⎞

⎜⎟

−−

⎜⎟

−−

⎜⎟

−−

⎝⎠

. (3)

If we consider the following matrix,

⎛⎞

⎜⎟

⎝⎠

then, we can compute x in a single step as given by,

⎛⎞

=×× =

⎜⎟

⎝⎠

JX J JX J

xKXK

JX J JX J

. (4)

Since the DCT of an

block can be defined as

××YTxT

, (5)

where T is the DCT kernel matrix, then, it follows

that,

××× ×YTKXK T. (6)

From (6) we can define the transcoding matrix S as,

×STK. (7)

The structure of matrix

S is given by,

000 0 0 0

00 0 0

00 000 0

00 0 0

bcdebcd e

gfg

hijkhijk

lmno lm n o

fgf

pqrspqr s

⎛⎞

⎜⎟

−−

⎜⎟

−−

⎜⎟

−

⎜⎟

−−

⎜⎟

−−

⎜⎟

−−

⎝⎠

(8)

with

1.4142 1.2815 0.4618 0.1065

0.0585 1.1152 0.0793 0.45

0.8399 0.7259 0.0461 0.3007

0.4319 1.0864 0.5190 0.2549

0.2412 0.5308 0.9875

abcd

efgh

ijkl

mnop

qrs

====−

===−=

=− = = =−

==−=

The shown S matrix values are rounded to four

decimal places.

3 FAST ALGORITHM

The proposed fast IT-to-DCT conversion algorithm

is based on the symmetry properties of the S matrix

shown in (8). As it shall be explained, this

characteristic of the S matrix is exploited for

achieving fast computation of the transform

conversion.

Since the conversion defined by (1) is separable,

it can be computed by columns followed by rows. If

we define

z as an input 8 point column vector and Z

its 1D conversion, then, by using the horizontal

symmetry of the S matrix, we can use the following

fast algorithm to compute Z as,

SIGMAP 2006 - INTERNATIONAL CONFERENCE ON SIGNAL PROCESSING AND MULTIMEDIA

APPLICATIONS

[1] [5]

[2] [6]

[3] [7]

[4] [8]

[3] [7]

[2] [6]

mzz

=−

, (9)

23 45

23 4 5

2345

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

Zam

bm cm dm em

Zfmgm

hm im jm km

Zam

lm mm nm om

Zgmfm

pm qm rm sm

=×

=× +× +× +×

=× +×

=× +× +× +×

=×

=× + × +× +×

=× +×

=× +× +× +×

. (10)

This algorithm needs 22 multiplications and 22

additions, i.e., a total of 44 operations to perform

one 1D conversion. The full 2D fast conversion

algorithm needs

8442 704××= operations.

Instead, the pixel domain approach needs four

inverse IT (320 operations) and one direct DCT (672

operations) which yields a total of 992 operations.

(Xin et al. 2004, Lee et al 2005). Thus, the proposed

fast algorithm significantly reduces the number of

operations (29%) when compared to the pixel

domain conversion.

4 INTEGER APPROXIMATION

In order to achieve higher computing performance,

we have further introduced an integer approximation

of the matrix

S . This is of particular relevance for

fixed-point arithmetic hardware, which is much

faster than floating point. The ultimate generation of

DSPs operate with clock frequencies of 300MHz for

floating-point architectures, while that of fixed-point

architecture is about 1GHz (Texas Instruments,

2004).

In order to work with integer arithmetic, we scale

the

S matrix by multiplying it by an integer that is a

power of 2. To represent each H.264 residual pixel

value, we need 9 bits and to perform the IT, we need

11 bits to represent the coefficients. The maximum

gain of the 2D

S -transcoding matrix is

4.67

which implies that more 5 bits are needed to

represent the result of the conversion. Therefore, the

scaling factor must be smaller or equal than the

square root of

(

)

32 16

22 256−=

. The integer S matrix

version is given by,

(256 )

int

round

×SS

, yielding

int

'0 00 ' 0 0 0

'''' '' ''

0'0'0 '0 '

'' '' '' ' '

00 '00 0 ' 0

'''''' ''

0'0'0'0 '

'''' '' ''

bcde bc de

gfg

hi jk hi jk

lmno lm no

fg f

pqrs pq r s

−−

⎛⎞

⎜⎟

⎝⎠

The corresponding

int

S values are given by,

' 362 ' 328 ' 118 ' 27

' 14 ' 285 ' 20 ' 115

' 227 ' 185 ' 11 ' 75

' 110 ' 278 ' 132 ' 65

' 61 ' 136 ' 352

abcd

efgh

ijkl

mnop

qrs

====−

===−=

=− = = =−

==−=

Since the

int

S matrix symmetries are similar to

S, thus, we can also apply the fast algorithm

described in section 3.

4.1 Multiplierless Implementation

In order to reduce, even more, the computational

complexity of the proposed integer conversion

algorithm, we may not use hardware multipliers. It is

possible to identify in (10) the following multiple

constants multiplication boxes,

12 23 34

45 56 68

bcd

hi j

bm bm bm

lmn

pqr

kfg

bm bm bm

og f

⎡

⎤⎡⎤⎡⎤

⎢

⎥⎢⎥⎢⎥

⎢

⎥⎢⎥⎢⎥

=× =× =×

⎢

⎥⎢⎥⎢⎥

⎢

⎥⎢⎥⎢⎥

⎣

⎦⎣⎦⎣⎦

⎡⎤

⎢⎥

⎡

⎤⎡⎤

⎢⎥

=× =× =×

⎢

⎥⎢⎥

⎢⎥

⎣

⎦⎣⎦

⎢⎥

⎣⎦

which are easily implemented using only elementary

operations, i.e., additions, subtractions and shifts

FAST CONVERSION OF H.264/AVC INTEGER TRANSFORM COEFFICIENTS INTO DCT COEFFICIENTS

(Puschel et al. 2004), The number of low complexity

operations required to compute each multiplier box

is shown in Table 1.

Table 1: Number of operations per multiplier block.

Block Add/Sub Shift Neg

b 5 7 2

b 5 7 1

b 6 7 1

b 4 7 1

b 3 4 1

Table 2 shows the number of clock cycles required

by a general purpose processor (Intel, 2001) to

compute each

multiplier block, (column Mb) as well

as the conventional multiplier method (column

Mu).

As it can be seen, the number of clock cycles

required by the integer fast approximation based on

multiplier blocks is about 61% of those required by

the conventional method.

Table 2: Number of clock cycles per block operations.

Block Add/Sub Shift Neg Mb Mu

b 5 35 2 42 68

b 5 35 1 41 68

b 6 35 1 42 68

b 4 35 1 40 68

b 3 20 1 24 34

5 EXPERIMENTAL RESULTS

We have evaluated the error introduced by integer

approximation of the

S matrix by comparing both

methods described in previous sections.

A set of 3 different grey level images was used

(256x256, 8 bit/pel). For each one, the whole image

was transformed into

IT coefficient blocks.

Then, each group of four adjacent

coefficient blocks are DCT converted by means of

two different methods: i) the full precision algorithm

described in section 2; ii) the integer approximation

described in section 4. The mean squared error

(MSE), between both resulting images (pixel

domain), was used for evaluating the error

introduced by the integer approximation method.

The results are shown in Table 3, where it can be

seen that the error due to the integer approximation

in the conversion process is actually very small. In

fact, the resulting MSE is negligible in practical

terms, which proves the usefulness of the proposed

method for fast transcoding implementations.

Table 3: MSE of the integer approximation.

Image Einstein Smandril Cameraman

MSE 0.337 0.339 0.340

6 CONCLUSIONS

In this paper, we proposed a transform domain

approach for fast conversion H.264/AVC 4x4

Integer Transform to standard

DCT. We derived the

conversion matrix and an efficient algorithm for

computing the transform, as well as, a low

complexity integer approximation method. The

presented results show that the proposed methods

are much faster than the pixel domain approach.

These methods are suitable for video transcoding

applications where fast processing is required.

REFERENCES

Chuang, S.,Vetro, A., 2005. Video Adaptation: Concepts,

Technologies, and Open Issues In

Proceedings of the

IEEE

, vol. 93, no. 1, pp 148-158.

Intel, 2001. Intel Pentium 4 Processor Optimization

Reference Manual, Order Number 248966

Lee, J., Chung, K., 2005. Quantization/DCT conversion

Scheme for DCT-Domain MPEG-2 to H.264/AVC

Trascoding. In

IECIE Trans. Commun., vol E88-B.

Malvar, H., Hallapuro, A., Korczewicz, M., Kerofsky,

L.,2003. Low-Complexity Transform and

Quantization in H.264/AVC. In

IEEE Transactions on

Circuits and Systems for Video Technology

, vol 13, pp

598-603.

Pushel, M, Voronenko, Y., 2004. Multiplierless Constant

Multiplication, Spiral Project, Carnegie Mellon

University ( http://www.spiral.net).

Sullivan, G., Topiwala, P., Lu, A., 2004. The H.264/AVC

Advanced Video Coding Standard: Overview and

Introduction to the Fidelity Range Extensions.

In SPIE

Conference on Applications of Digital Image

Processing XXVII

Texas Instruments, 2004. TMS 320C600 CPU and

Instruction Set Reference Guide. Literature Number

SPRU189F.

Xin, J., Vetro, A., Sun, H., 2004. Converting DCT

Coefficients to H.264/AVC Transform Coefficients. In

Technical Report of Mitsubishi Electric Lab. TR-

2004-058.

SIGMAP 2006 - INTERNATIONAL CONFERENCE ON SIGNAL PROCESSING AND MULTIMEDIA

APPLICATIONS