
SIGNAL DENOISING BASED ON PARAMETRIC HAAR-LIKE
TRANSFORMS
Susanna Minasyan, Karen Egiazarian, Jaakko Astola
Tampere University of Technology, Tampere, Finland,
David Guevorkian
Nokia Research Centery,Tampere,Finland
Keywords: Signal denoising, Wavelet, Threshold, Parametric transform.
Abstract: Orthogonal transforms have found considerable interest in signal denoising applications. Recently
Parametric Haar-like Transforms (PHTs) have been introduced and shown to be efficient in image denoising
and compression applications. PHT is such that it may be computed with fast algorithm in structure a
similar to that of classical fast Haar transform and such that its matrix contains a predefined basis vector,
called generating vector, as its first row. PHT may be adapted to the characteristics of the input signal or to
its parts by a proper selection of the generating vectors. Possibility of adaptation to the input signal may, in
principle, be significant source for performance improvement of transform based signal processing
algorithms. In this paper, the capability of parametric Haar-like transforms, in 1-D signal denoising
application is explored. A new PHT based post-processing algorithm for 1-D signal denoising is proposed,
which may be combined with another denoising method in order to improve the quality of the output signal.
Experiments were conducted where the basic wavelet thresholding based signal denoising method was
complemented with the proposed post-processing algorithm. Simulation results illustrate significant
performance improvement due to the use of the proposed algorithm.
1 INTRODUCTION
One of the most important problems in signal
analysis is noise suppression or denoising where the
problem is to find an estimate of a signal that was
corrupted by a noise, e.g. additive Gaussian noise.
Conventional denoising methods, in particular,
Wiener filtering, are based on linear methods. Non-
linear methods such as filtering in wavelet transform
domain or wavelet-thresholding introduced by
Donoho and Johnstone (Donoho et al, 1994),
(Donoho, 1995), have also been shown be very
efficient in signal denoising. Mostly, wavelet
denoising was focused on statistical modeling of
wavelet coefficients and optimal choice of threshold
values (Grace Chang et al, 2000). In practice, the
most commonly applicable are soft and hard
thresholding functions. Recently, another function
called customized thresholding was proposed (Yoon
et al, 2004) that depends on a set of parameters and
can be adapted to the input signal. The customized
thresholding function combines advantages of
traditional soft and hard thresholding, it can become
either one of them by setting parameter values. The
idea of customized thresholding is similar to that of
semi-soft or firm shrinkage (Gao, 1996) and the non-
negative garrote thresholding function (Gao, 1998).
It was shown that custom thresholding function
outperforms the traditional ones and it improves
denoising results significantly.
Besides wavelets, different other orthogonal
transforms (Egiazarian et al, 1999, Pogossova et al,
2003, Oktem et al, 1999) such as Fourier and DCT,
Haar, combination of DCT and Haar, Tree-
Structured Haar Transforms (THT), Generalized
Lapped transforms and others have been proposed as
useful tools in signal denoising applications. In
many cases local transform based denoising methods
are more profitable than wavelet based denoising
methods which are applied to the whole signal.
134
Minasyan S., Egiazarian K., Astola J. and Guevorkian D. (2006).
SIGNAL DENOISING BASED ON PARAMETRIC HAAR-LIKE TRANSFORMS.
In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 134-139
DOI: 10.5220/0001570401340139
Copyright
c
SciTePress

Recently there has been considerable interest in
constructing signal adapted systems for signal
denoising, compression, and other applications
(Egiazarian et al, 1999, Oktem et al, 1999,
Pogossova et al, 2003). Thereby, parametric
transforms with matrices described in a unified form
involving a set of parameters are of interest
nowadays. In this context parametric transform
means a wide class of discrete orthogonal transforms
(DOTs) that may include classical transforms and an
infinite number of new transforms with the
possibility to select the desired transform according
to parameter values. A unified software/hardware
tool can be used to implement the whole class of
transforms with the possibility to adjust transform
parameters. One can find various methods of
synthesizing the parametric transforms in (Agaian et
al, 1992).
In particular a family of parametric Haar-like
transforms was introduced (Minasyan et al, 2001).
Parametric Haar-like transform (PHT) is such a
DOT that its matrix contains a desired basis function
as its first row and such that it may be computed by
a fast transform algorithm in structure similar to that
of the classical fast Haar transform algorithm.
Efficiency of using PHTs in image compression
(Minasyan et al, 2005) as well as in image denoising
(Minasyan et al, 2006) has motivated a study of their
usefulness also in 1-D signal denoising.
The goal of this paper is to investigate the
potential of PHTs in improving the performance of
signal denoising. A new signal denoising algorithm
is proposed where the corrupted signal is
transformed into the transform domain with PHTs
that are synthesized according to a signal estimate
obtained, e.g. by wavelet denoising. The input noisy
signal and its estimate are split into small sized
windows. For every small window of the estimate
one PHT is synthesized such that its matrix has the
contents of the window as its first row. This PHT is
applied to the corresponding window of the
corrupted noisy signal. Next, the transformed
coefficients are thresholded by customized threshold
(Yoon et al, 2004) and transformed back into the
original domain by the inverse PHT. Simulations
were conducted on several test signals showing
significant improvement in reducing the noise as
compared to the pure wavelet denoising method.
The paper is organized as follows: Section 2
gives a brief introduction to PHT’s. Background on
wavelet thresholding methods is given in Section 3.
Section 4 is the description of the proposed PHT
based denoising algorithm. Section 5 describes
simulations and results of experiments. The
conclusion is given in Section 6.
2 PARAMETRIC HAAR-LIKE
TRANSFORM (PHT)
Orthogonal transforms are widely used in
signal/image processing, in particular, for signal
denoising. In practice, different well-known fixed
transforms with fast algorithms such as Discrete
Fourier, Cosine, Sine, Haar, and Hadamard
transforms are commonly used. Each of these
transforms is suitable for a particular type of input
signals but none of them performs sufficiently well
on different types of input signals. Performance of
fixed transforms, in particular, in signal denoising
may be increased by making use of parametric,
signal adaptive transforms. In a parametric transform
based method different transforms may be
synthesized and applied to different signals or even
to different parts of a signal.
One way of synthesizing parametric transforms
is based on unified representations of fast transform
algorithms (see Agaian et al, 1992), (Minasyan et al,
2001). Such unified representation is based on
factorization of transform matrix of an arbitrary
order N as a product of block-diagonal sparse
matrices and permutation matrices. Blocks of sparse
matrices along with permutation matrices play the
role of synthesis parameters. One can vary these
parameters to synthesize an infinite number of
different transforms all a priori possessing fast
algorithms for their computation. It is also possible
to adjust the parameters to design a transform matrix
having some desired features. Good examples of
synthesising such parametric transforms are the
Haar-like, Hadamard-like transforms which have
been proposed in (Minasyan et al, 2001) where, in
particular, a method was proposed for constructing
an orthogonal Haar-like or Hadamard-like transform
matrix such that its first row is a predefined
normalized vector
01
,...,
N
hh h
−
=
⎡
⎤
⎣
⎦
called generating
vector. In (Minasyan et al, 2001), one can find the
detailed description of constructing a parametric
orthogonal Haar-like transform of order N=2
m
,
which involves the generating vector. The transform
matrix has such a structure that its first row
(column) is the generating vector while the rest of
the basis functions are orthogonal to the first row.
And, there is a fast algorithm for every Haar-like
transform implementation similar to that of classical
fast Haar transform algorithm.
SIGNAL DENOISING BASED ON PARAMETRIC HAAR-LIKE TRANSFORMS
135

It should be noted that the generating vector for
the classical discrete Haar transform of order N=2
m
is the constant (1x2
m
)-vector (with all components
equal to each other). Using other generating vectors
of arbitrary length and arbitrary component values
an infinite number of Haar-like transforms, similar
in structure to the Haar transform, may be
synthesized.
Let us consider an example of synthesizing a
Haar-like transform of order N=8 with the
generating vector
()
[]
1 204 1, 2,3, 4,5,6,7,8=⋅h
on its first row. The matrix
8
H
of the desired
transform is supposed to be presented as:
(4) (3) (3) (2) (2) (1) (1)
8
H
PHPH PH P= ,
where we define
(1) (4)
8
PP I==
. Then, we define
12 34 5 6
11 1
(1)
21 43 65
5
561
78
1
87
113
H
⎡⎤⎡⎤ ⎡⎤
=⊕⊕⊕
⎢⎥⎢⎥ ⎢⎥
−− −
⎣⎦⎣⎦ ⎣⎦
⎡⎤
⊕⋅
⎢⎥
−
⎣⎦
With this matrix we obtain the result of the first
stage:
()
(1)
1
5, 0,5,0, 61,0, 113,0 .
204
T
H
⎡⎤
== ⋅
⎣⎦
1
xh
We then define the permutation matrix
(2)
(8)
sh
PP= to be the perfect shuffle of order 8.
Applying
)2(
P
to
1
x results in
(2)
1
(1 204) 5,5, 61, 113, 0,0,0,0 .
T
P
⎡⎤
=⋅
⎣⎦
x
Now we define
)2(
H
as:
5 5 61 113
11
(2)
4
30 174
55 11361
H
I
⎡⎤⎡ ⎤
=⊕ ⊕
⎢⎥⎢ ⎥
−−
⎢⎥⎢ ⎥
⎣⎦⎣ ⎦
.
Applying this matrix to
(2)
P
1
x
yields:
(2) (2)
1 204 30,0, 174,0,0,0,0
T
HP
⎡
⎤
==
⎣
⎦
21
xx .
Taking
(3) ( )
4
(4)
sh
PP I=⊕ and defining
(3)
6
30 174
1
204
174 30
H
I
⎡⎤
=⊕
⎢⎥
−
⎢⎥
⎣⎦
,
we will find
[]
(3) (3)
1, 0,0,0, 0, 0,0,0
T
HP==
32
xx .
Substituting the defined matrices into the
factorization of
8
H
we obtain the desired matrix:
8
12345678
2.4 4.8 7.2 9.6 2.1 2.5 2.9 3.3
5.8 11.7 3.5 4.7 0 0 0 0
0 0 0 0 7.4 8.8 5.6 6.4
1
12.8 6.4 0 0 0 0 0 0
204
0 0 11.4 8.6 0 0 0 0
0 0 0 0 10.9 9.1 0 0
0 0 0 0 0 0 10.7 9.4
H
≈
⎡
⎤
⎢
⎥
−−−−
⎢
⎥
⎢
⎥
−−
⎢
⎥
−−
⎢
⎥
⋅
⎢
⎥
−
⎢
⎥
−
⎢
⎥
⎢
⎥
−
⎢
⎥
−
⎢
⎥
⎣
⎦
PHT is an input-adapted transform that may be
adjusted to the input signal to improve the
performance of fixed transforms in different
applications. It has recently been shown that PHT
may efficiently be used in image compression
applications (Minasyan et al, 2005) and also in
image denoising (Minasyan et at, 2006). This
motivated us to study the PHT also in signal
denoising.
3 WAVELET THRESHOLDING
FUNCTIONS
Let y=x+z be a (1xN) input noisy signal, x be
corresponding noiseless signal and z be Gaussian
white noise with N(0, σ
2
).
Transform–based approach to noise reduction
problem consists of following steps:
1. Transform the noisy signal into the
corresponding transform domain;
2. Apply some thesholding to the resulting
coefficients by zeroing out the coefficients
lower than a certain amplitude;
3. Transform back to the original domain,
performing the inverse transform.
One of the best known denoising methods is
based on using a discrete wavelet transform at Step 1
(and corresponding inverse discrete wavelet
transform at Step 3). The most commonly used
thresholding functions at Step 2 are the hard-
thresholding and soft-thresholding functions.
Recently, the custom thresholding function (CTF)
was introduced .
a) The hard-thresholding function selects
(significant) wavelet coefficients that are greater
than the given threshold λ and sets the others to
zero:
, if λ
()
0, otherwise.
h
f
⎧
≥
⎪
=
⎨
⎪
⎩
xx
x
(1)
SIGMAP 2006 - INTERNATIONAL CONFERENCE ON SIGNAL PROCESSING AND MULTIMEDIA
APPLICATIONS
136

The hard-thresholding function is discontinuous
at threshold λ, e.g. at |x| = λ. That is why the
artifacts, known as Gibbs phenomena, near the
discontinuities appear in the denoised signal.
b) The soft-thresholding function, which is called
also wavelet shrinkage function, shrinks the wavelet
coefficients by threshold λ towards zero:
λ, if λ
() 0, λ
+λ, if -λ.
s
f
−≥
⎧
⎪
=<
⎨
⎪
≤
⎩
xx
xx
xx
(2)
c) The custom-thresholding function, (CTF):
()
2
()(1 )λ, if | | λ
( ) 0, if
3 4 otherwise(){ () },
c
sgn
f
⎧
⎪
−−α ≥
⎪
⎪
=≤γ
⎨
⎪
−γ −γ
⎪
αλ α − + − α
⎪
λ−γ λ−γ
⎩
xx
xx
xx
x
(3)
where γ is the cut-off value, below which the
wavelet coefficients are set to zero, 0< γ < λ , and α
is the parameter that decides the shape of the
thresholding function f
c
(x), 01.≤α≤ This function
is continuous at λ and can be adapted to the signal
characteristics.The customized thresholding function
may be considered as a linear combination of soft-
thresholding function and hard thresholding function
() () (1 ) ()
ch s
ff f=α⋅ + −α ⋅xx x that is continuous
around the threshold λ. By varying the parameters α,
γ and λ, it is possible to vary the CTF between the
soft and hard thresholding functions or just to switch
from one function to another one.
4 PHT-BASED POST ROCESSING
ALGORITHM FOR SIGNAL
DENOISING
The proposed denoising algorithm belongs to the
general class of transform based denoising
algorithms described in Section 3 where we use the
Parametric Haar-like Transforms (PHT) as the
invertible transform of Step 1 (and its inverse at Step
3). The idea of the proposed algorithm is to use the
signal adapted PHTs instead of fixed orthogonal
transforms in order to better distinguish between
signal and noise in the transform domain. The main
point consists in finding the suitable generating
vectors for PHT synthesis. In an ideal case, if the
generating vectors would be taken from the original
uncorrupted signal, then the whole energy of the
corrupted signal in the transform domain would be
concentrated in only the first transform coefficient.
By zeroing out all the rest coefficients would
remove almost all the noise while would preserve
the original signal untouched. However, since in
reality the original signal is unknown, we may only
use its estimate to form the generating vectors for
PHT synthesis. As such an estimate we use the result
of wavelet denoising. It has been shown that
VisuShrink tends to oversmooth the signal, leading
to loss of details and increase estimation error.
Taking this into account we use the CTF.
The proposed algorithm (Wavelet-PHT
denoising algorithm) may be described in four steps:
1. The input signal is denoised by wavelet
transform to find an estimate of an
uncorrupted signal.
2. The input signal is transferred window by
window (which are non-overlapping) into
the transform domain by PHTs that are
synthesized on the base of the estimate of
the original signal in the corresponding
window obtained at Step 1. Thus, both the
original signal and the estimate are divided
into non-overlapping windows, for
instance, of length 8. For each window of
the estimate the PHT containing the
corresponding window content as its first
row is synthesized. Then, it is applied to the
window of the original signal at the same
location.
3. The customized thresholding is applied to
each transformed window. The parameters
α, λ and γ of the thresholding function were
determined empirically.
4. Then, each thresholded window is
transformed back with inverse PHTs. Note
that the direct and inverse PHTs may be
computed with fast algorithms in structure
similar to that of Haar transform.
5 SIMULATION RESULTS
The proposed method was tested on different
artificial test signals such as Blocks, Bumps,
HeavSine, Doppler, Cusp of length 256 taken from
Matlab’s WaveLab toolbox. The signals were
corrupted by additive Gaussian noise with SNR
(signal-to-noise-ratio) 7 and then denoised by the
proposed algorithm. In all the experiments bellow
the Daubechies asymmetric wavelet with 8
vanishing moments and 8 decomposition levels was
used at Step 1 of the algorithm. The results of the
experiments were averaged over 30 runs.
SIGNAL DENOISING BASED ON PARAMETRIC HAAR-LIKE TRANSFORMS
137
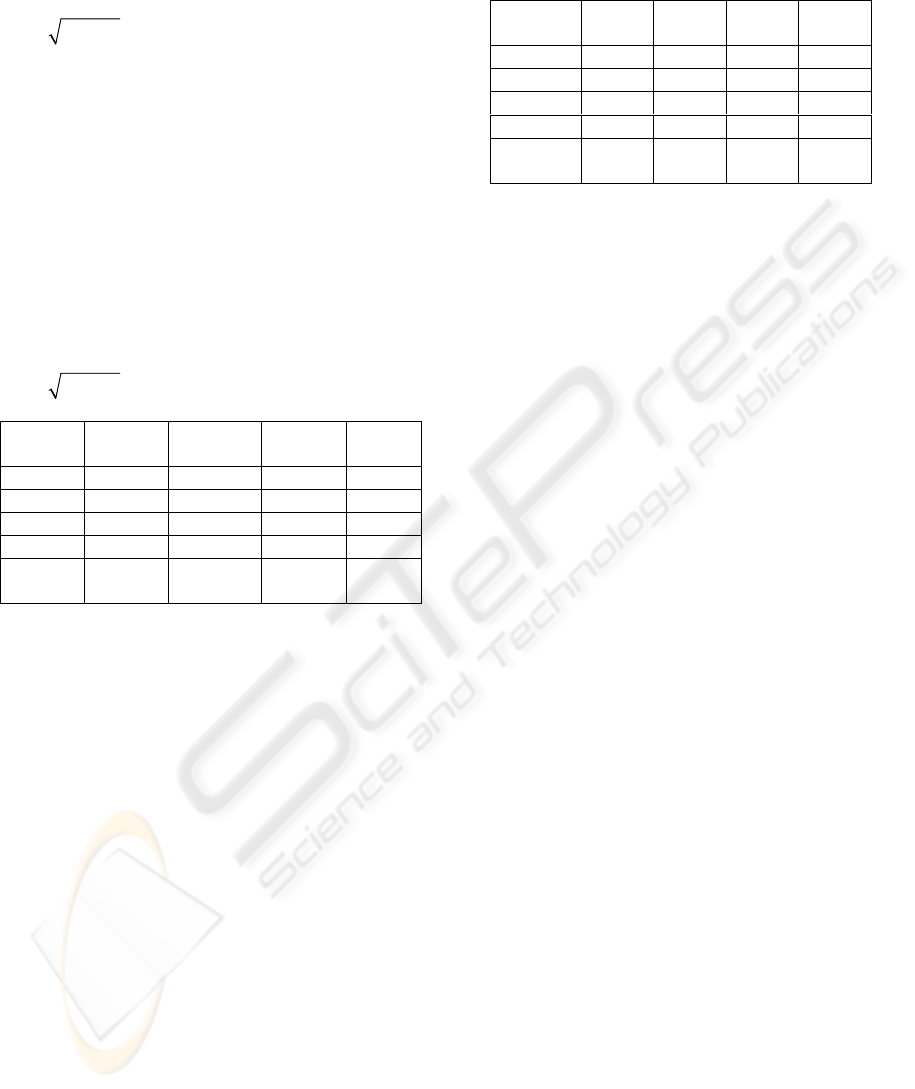
Table 1 presents the results of one set of
experiments. In this experiment soft and hard
threshoding with the universal threshold
2logNλ=σ were used both in wavelet denoising
and in PHT post-processing where N is a length of a
signal in the case of wavelet denoising and N=w=8
is a window size in PHT post-processing. The
second and third columns correspond to soft
thresholding of both wavelet coefficients and PHT
coefficients. The fourth and fifth columns
correspond to the case of hard thresholding. One can
see that in the most of the cases the proposed
method (third column) reduces significantly noise in
the sense of MSE comparing with MSE of soft
thresholded estimate.
Table 1: Comparative results of MSE averaged over 30
runs: denoising with the universal threshold
2logNλ=σ .
Table 2 presents the results of another set of
experiments where the soft and customized
thresholding functions were applied with empirically
optimized thresholding parameters in order to
explore potential of the proposed method.
The second column of Table 2 represents the
MSEw values of wavelet denoising using soft
thresholding with optimized threshold values λ
w
given in the fourth column of the table
.
In the third column the values MSEwp obtained
after PHT-based post-denoising are given. Again
window size was chosen w=8 but now CTF with
optimized parameter values
λ
wp
(see column 5), and
fixed
0.97=
α
and γ =0.9·λ were used (these values
were experimentally found as the optimal for all the
experimented signals).
Table 2: Comparative results of MSE averaged over 30
runs: denoising with empirically found optimal thresholds.
The experiments have shown that for each signal
the optimal ranges of threshold values λ
wp
which
have been used in proposed denoising method for
signals Blocks, Bumps, Doppler, Cusp and
HeaviSine are 4~7.5, 5~7, 2.5~3.5, 3~8 and 3~3.8,
respectively.
Besides, for each signal the confidence intervals
(CI) for MSEwp values were obtained during the
experiments. In particular, CI for Blocks is [0.42,
0.69], CI for Bumps is [0.38, 0.57], CI for Doppler
is [0.32, 0.66], CI for Cusp is [0.13, 0.30] and CE
for HeaviSine is [0.20, 0.53].
It can be seen that by applying the proposed
denoising the remaining noise is reduced
significantly in the sense of MSE.
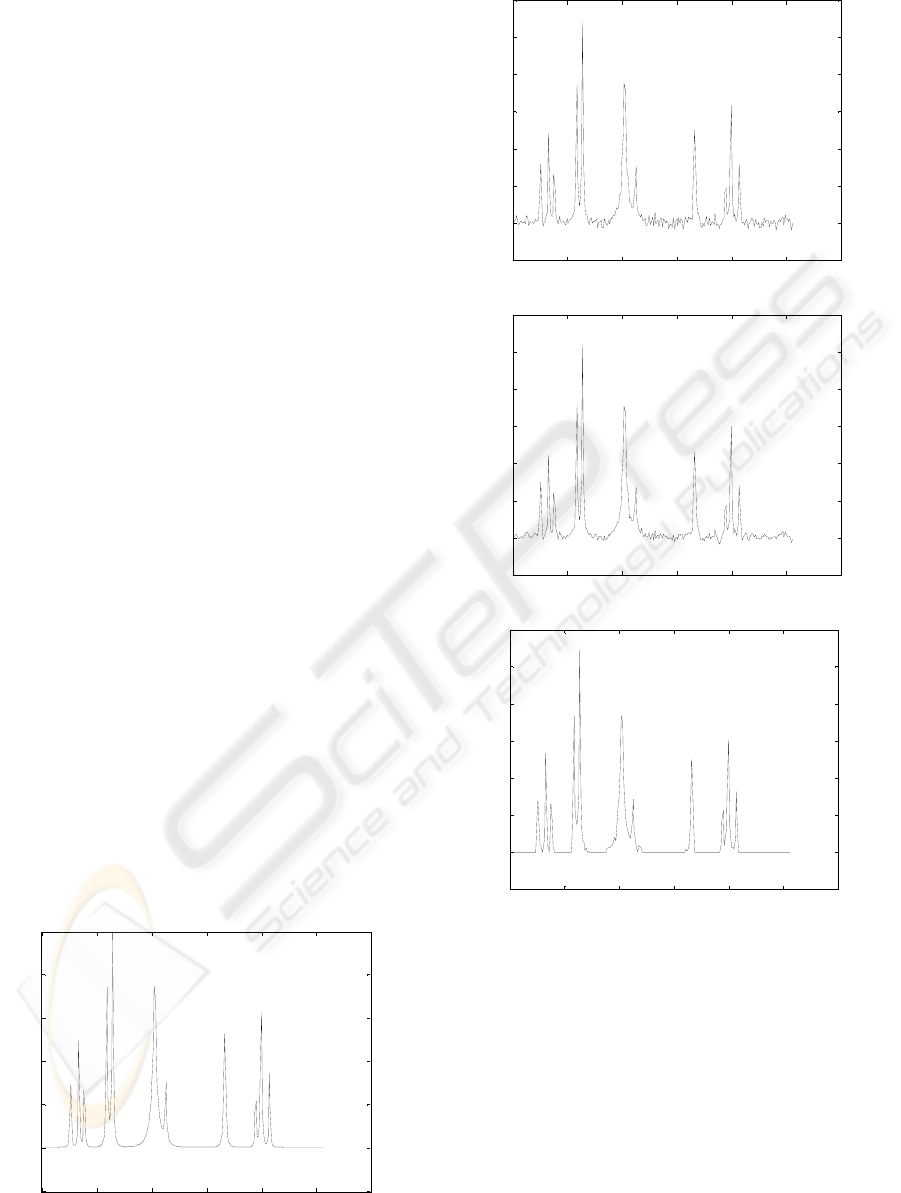
Fig. 1 illustrates the performance of the proposed
algorithm on the example of the signal Bumps. One
can see that the result of the proposed algorithm
(Fig.1,d) is significantly closer to the uncorrupted
signal (Fig.1,a) as compared to the result of the pure
wavelet denoising (Fig.1,c). Performance
improvement is similar for other signals as well.
6 CONCLUSION
A method based on parametric Haar-like transforms
for improving wavelet denoising is presented here. It
employs a parametric Haar-like transform that can
be custom designed for each part (window) of the
signal. The simulation results verify the efficiency of
the proposed method. Similar algorithm may be
extended also to image denoising application.
REFERENCES
Donoho, D.L., and Johnstone, I.M., 1994. Ideal Spatial
Adaptation via wavelet shrinkage, Biometrika.
Donoho, D.L., 1995. De-noising by soft thresholding,
IEEE Transactions on Information Theory.
Signal Soft
PHT
soft
Hard PHT
hard
Blocks 4.18 0.96 1.33 0.82
Bumps 4.62 0.94 1.16 0.76
Doppler 2.34 0.65 0.67 0.63
Cusp 0.70 0.18 0.29 0.39
Heavi
Sine
1.09 0.24 0.35 0.41
Signal MSEw
MSEw
p
λ
w
λ
wp
Blocks 0.84 0.57 0.9 6
Bumps 0.81 0.47 0.7 5
Doppler 0.63 0.48 1.3 3
Cusp 0.50 0.19 2.7 7
Heavi
Sine
0.88 0.29 3 3
SIGMAP 2006 - INTERNATIONAL CONFERENCE ON SIGNAL PROCESSING AND MULTIMEDIA
APPLICATIONS
138
Chang, S.G., Yu,B., Vetterli, M., 2000. Adaptive wavelet
thresholding for image denoising and compression,
IEEE Transactions on Image Proccessing.
Yoon, B.-J., Vaidyajnathan, P.P., 2004. Wavelet-based
de-noising by customized thresholding. In ICASSP’04.
Proc.29th IEEE International Conference on
Acoustics, Speech, and Signal Processing.
Gao, H.-Y., 1996. WaveShrink with firm shrinkage,
Technical Report 39, StatSci Division of MathSoft,
Inc.
Gao, H.-Y., 1998. Wavelet Shrinkage de-noising using the
nonnegative garrote, Journal on
Comput.Graph.Statist.
K.Egiazarian, M Helsingius, and J.Astola, 1999. Removal
of Blocking Artifacts using Transform Domain
Denoising, In ISCAS’99.
Egiazarian, K., Astola, J., Helsingius, M., Kuosmanen P.,
1999. On Adaptive Denoising and Lossy Compression
of Images in Transform Domain, Journal of Electronic
Imaging, SPIE.
Pogossova, E., Egiazarian, K., Astola, J., 2003. Signal De-
noising in Tree-Structured Haar-basis, Proc. of 3
rd
International Symposium on Image and Signal
Processing and Analysis.
Öktem,R., Yaroslavsky, L., Egiazarian, K., 1999.
Transform based Denoising Algorithms: Comparative
Study, TICSP Series #9, Tampere, Finland.
Agaian, S.S., Gevorkian, D.Z., 1992. Synthesis of a class
of orthogonal transforms. Parallel SIMD-algorithms
and specialized processors. Pattern Recognition and
Image Analysis.
Minasyan, S., Guevorkian, D., Sarukhanyan, H., 2001. On
parameterized fast Haar- and Hadamard-like
transforms of arbitrary order, In CSIT’01. Proc. of 3
rd
International Conference On Computer Science and
Information Technologies.
Minasyan, S., Astola, J., Guevorkian, D., 2005. An Image
Compression Scheme Based on Parametric Haar-like
Transform. In ISCAS’05. Proceedings of IEEE
International Symposium on Circuits and Systems.
Minasyan, S., Astola, J., Egiazarian, K., Guevorkian, D.,
2006. Parametric Haar-like Transforms in Image
Denoising. In ICIP’06. International Conference on
Image Processing.
0 50 100 150 200 250
-10
0
10
20
30
40
a)
0 50 100 150 200 250 300
-10
0
10
20
30
40
50
60
b)
0 50 100 150 200 250 300
-10
0
10
20
30
40
50
60
c)
0 50 100 150 200 250 300
-10
0
10
20
30
40
50
60
d)
Figure 1: Denoising of signal Bumps: a) Original signal, b)
noisy signal (SNR=7dB), c) wavelet denoised signal (soft
thresholded, MSEw=0.7111), and d) signal denoised by
proposed method (thresholded by CTF, w=8,
MSEwp=0.3735).
SIGNAL DENOISING BASED ON PARAMETRIC HAAR-LIKE TRANSFORMS
139
