
PACKET SCHEDULING AND PRICING BASED ON INFLICTED
DELAY
Ari Viinikainen
Department of Mathematical Information Technology, University of Jyväskylä
P.O. Box 35 (Agora)
40014 University of Jyväskylä, Finland
Keywords:
Pricing, revenue optimization, delay, Quality of Service (QoS).
Abstract:
An adaptive packet scheduling method is presented in this paper. The adaptive weights of a scheduler are
chosen based on maximizing the revenue of the network service provider. The pricing scenario is based on
the delay that a connection will inflict to other connections. The features of the adaptive weight updating
algorithm are simulated, analyzed and compared to a constant weight algorithm.
1 INTRODUCTION
Internet services should be focused more on service
alignment and revenue generation. This requires new
ideas for network management solutions. To meet
growing organizational demands, policy-based man-
agement is one solution that will allow organiza-
tions to prioritize networking resources such as band-
width, application access and security clearance based
on individual users. These policy-based manage-
ment methods will have to be self-deploying, self-
configuring and self-healing, automatically discov-
ering any changes taking place in the network in-
frastructure and dynamically building and altering
policies for accessing resources based on needs. By
combining scheduling and revenue issues together an
efficient method can be built to allocate network re-
sources in optimal and profitable way.
The packet scheduling algorithms can be classi-
fied into two categories, depending on the need for
sorting the packets in the scheduler. Those that are
based on packet sorting, need to maintain a “virtual
time”, that is used to calculate the order of the pack-
ets. These kinds of schedulers provide good fair-
ness and low latency but due to the complexity in
computation of the parameters used for sorting, they
lack efficiency. Weighted Fair Queueing (WFQ) (De-
mers et al., 1989; Parekh and Gallager, 1993) was
a first proposal of these kinds. Later other propos-
als as Self-clocked Fair Queueing (SCFQ) (Golestani,
1994), Worst-case Fair Weighted Queueing (WF
2
Q)
(Bennett and Zhang, 1996), Start-time Fair Queue-
ing (SFQ) (Goyal et al., 1997) and Frame-Based Fair
Queueing (FFQ) (Stiliadis and Varma, 1998) have
been proposed to combat the lack of efficiency.
Schedulers that handle packets in a round robin
manner, like Deficit Round Robin (DRR) (Shreed-
har and Varghese, 1996), are in the other category.
These have low complexity but they are not as good
in fairness and latency. Several algorithms have been
proposed for improving the latency and fairness in a
round robin based schemes, such as Advanced Round
Robin (ARR) (Marosits et al., 2001), Smoothed
Round Robin (SRR) (Guo, 2001), Pre-order deficit
round robin (Tsao and Lin, 2001), Nested DRR (Kan-
here and Sethu, 2001), Elastic Round Robin (ERR)
(Kanhere et al., 2002), Stratified Round Robin (Ram-
abhadran and Pasquale, 2003) and Fair Round Robin
(FRR) (Yuan and Duan, 2005).
This paper proposes a scheduling model that guar-
antees that the latencies for different service classes
are appropriate and at the same time optimizes the
network service provider’s revenue. This work con-
tinues the work in (Viinikainen et al., 2004) and (Jout-
sensalo et al., 2005) where the pricing of a connec-
tion was based on delay and bandwidth that the con-
nection itself obtains, respectively. The proposed al-
gorithm that is presented in this paper ensures less
delay for the users paying more for the connection
(i.e. higher service class) than those paying less. The
proposed method also penalizes by pricing those cus-
tomers, who induce the most delay in the network.
Thus, this approach yields a tempting scenario for
customers and the service provider. The closed form
113
Viinikainen A. (2006).
PACKET SCHEDULING AND PRICING BASED ON INFLICTED DELAY.
In Proceedings of the International Conference on e-Business, pages 113-117
DOI: 10.5220/0001424201130117
Copyright
c
SciTePress

formula for updating weights is independent on any
statistical behavior of the connections. Therefore, it is
also robust against erroneous estimates of customers’
behavior.
The rest of the paper is organized as follows. First,
in Section 2 the scheduler is discussed and the pro-
posed pricing scenario is defined, whilst experiments
justifying the analytical derivation are made in Sec-
tion 3. Section 4 contains discussion of theory and
experiments and Section 5 concludes the study.
2 THE PACKET SCHEDULER
AND DELAY
Let us consider a packet scheduler which receives
packets to be delivered from m different queues (i.e.
classes). Now, let T be the processing time of the
classifier for transmitting a data packet from one
queue to the output of a packet scheduler. For any
connection k there are N
ik
(t) packets in the queue of
class i at some time t. Total number of packets in the
queue i at the time t is therefore
N
i
(t) =
K
i
(t)
X
k=1
N
ik
(t), (1)
where K
i
(t) is the total number of connections in the
class i at time t.
Now, every packet in the queue increases delay for
the other connections in the queue so a new connec-
tion k appearing at time t in class i will increase the
delay to the other connections by a value proportional
to N
ik
(t)
d
ik
(t) =
N
ik
(t)T
w
i
(t)
=
N
ik
(t)
w
i
(t)
, (2)
where T can be scaled to T = 1 without loss of gener-
ality and w
i
(t) = w
i
, i = 1, . . . , m are weights allo-
cated for each class as a new connection in any class
will inflict delay on the other classes depending on
amount of processing time of the scheduler allotted to
each class. The overall delay in class i is then
D
i
(t) =
K
i
X
k=1
d
ik
=
K
i
X
k=1
N
ik
w
i
, (3)
where the time index t has been dropped for conve-
nience until otherwise stated. The natural constraints
for the weights are
w
i
> 0 (4)
and
m
X
i=1
w
i
= 1. (5)
For every connection the pricing is based on the rela-
tive increase in delay that it produces. Every connec-
tion induce delay and those connections that induce
more delay than the connections on average will pay
more for the connection.
Definition 1. For each service class the function
P
i
=
K
i
X
k=1
K
i
r
i
+ s
i
d
p
ik
, r
i
> 0, s
i
> 0, p > 0 (6)
is called a polynomial pricing function.
In the polynomial pricing function r
i
is a base price
of a connection in the class i, s
i
is a penalty factor
that increases the price for those connections which
induce more delay and p assures that the price does
not grow too rapidly with the delay. The total revenue
of the operator is
R =
m
X
i=1
P
i
=
m
X
i=1
K
i
X
k=1
p
ik
=
m
X
i=1
K
i
X
k=1
K
i
r
i
+ s
i
d
p
ik
.
(7)
Theorem 1. Optimal weights for the revenue R under
the polynomial pricing model is
w
i
=
s
1
p−1
i
N
p
p−1
i
P
m
j=1
s
1
p−1
j
N
p
p−1
j
. (8)
when 0 < p < 1.
Proof. By using Lagrangian approach, the revenue
can be presented in the form
R =
m
X
i=1
K
i
X
k=1
K
i
r
i
+ s
i
N
p
ik
w
p
i
+ λ(1 −
m
X
i=1
w
i
). (9)
Optimal weights are obtained from the first deriva-
tive
∂R
∂w
i
=
K
i
X
k=1
−ps
i
N
p
ik
w
p−1
i
− λ = 0. (10)
Because Lagrangian solution
∂F
∂λ
= 0 (11)
yields
P
m
j=1
w
j
= 1, then
w
i
=
−ps
i
N
p
i
λ
1
p−1
=
(−ps
i
)
1
p−1
N
p
p−1
i
λ
1
p−1
P
m
j=1
w
j
=
(−ps
i
)
1
p−1
N
p
p−1
i
λ
1
p−1
P
m
j=1
(−ps
j
)
1
p−1
N
p
p−1
j
λ
1
p−1
=
s
1
p−1
i
N
p
p−1
i
P
m
j=1
s
1
p−1
j
N
p
p−1
j
. (12)
ICE-B 2006 - INTERNATIONAL CONFERENCE ON E-BUSINESS
114
From the expression (12) it is seen that λ has the form
λ
1
p−1
=
m
X
j=1
s
1
p−1
j
N
p
p−1
j
, (13)
or
λ =
m
X
j=1
s
j
N
p
j
. (14)
Thus the first order derivative is
∂R
∂w
i
=
K
i
X
k=1
−ps
i
N
p
ik
w
p−1
i
−
m
X
j=1
s
j
N
p
j
, (15)
and so the second order derivative is
∂
2
R
∂w
2
i
=
K
i
X
k=1
−(p − 1)
−ps
i
N
p
ik
w
p−2
i
< 0 (16)
when 0 < p < 1. In that condition, R is concave with
respect to the weights w
i
, and the optimal solution is
unique.
By using optimal weights (8), revenue R can be
expressed as follows:
R =
m
X
i=1
K
i
X
k=1
K
i
r
i
+
s
i
N
i
w
i
=
m
X
i=1
K
i
r
i
+
s
i
N
i
s
1
p−1
i
N
p
p−1
i
m
j=1
s
1
p−1
j
N
p
p−1
j
=
m
X
i=1
K
i
r
i
+ s
p−2
p−1
i
N
−1
p−1
i
×
m
X
j=1
s
1
p−1
j
N
p
p−1
j
. (17)
3 EXPERIMENTS
In this section the operation of the pricing algorithm
(6) with p =
1
2
and m = 3 service classes is demon-
strated by simulation. The optimal weights (12) are
compared with a constant weight (w
1
= 1/2, w
2
=
1/3 and w
3
= 1/6) version of the algorithm.
The processing time of the server is chosen as
T = 1/1000 s/packet. The life time of a connec-
tion is exponentially distributed. The arrival rates of
the connections are Poisson distributed and they are
α
1
= 0.30, α
2
= 0.40 and α
3
= 0.50 per unit
time for the gold, silver, and bronze classes, respec-
tively. The duration parameters (i.e. "decay rates")
for the connections are β
1
= 0.015, β
2
= 0.013 and
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
0
10
20
30
40
50
60
Time[s]
Number of connections
Bronze
Silver
Gold
Figure 1: Evolution of the number of connections as a func-
tion of time.
β
3
= 0.011, where the probability density functions
for the durations are
p
i
(t) = β
i
e
−β
i
t
, , i = 1, 2, 3 t ≥ 0. (18)
The number of unit times in the experiments was τ =
2000 which is 2 seconds using T as defined above. In
the experiments the pricing factors r
i
= 0 as they only
make a shift in the revenue curves (i.e. increase the
revenues). The penalty factors were chosen as s
1
=
10, s
2
= 15 and s
3
= 20 for gold, silver and bronze
classes, respectively. So connections causing delay in
the gold class are penalized less and those in bronze
class the most.
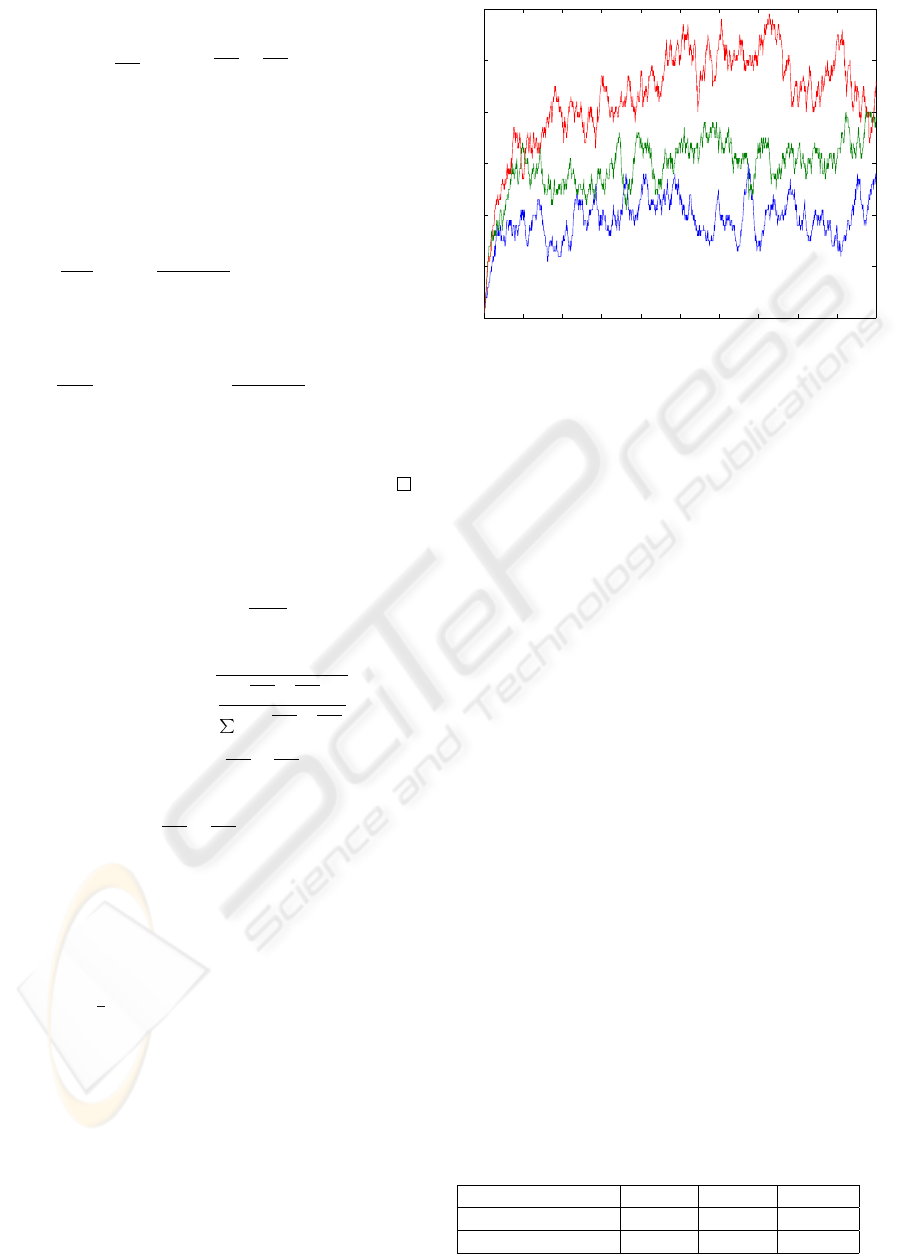
The number of connections on the average is high-
est for the bronze class and lowest for the gold class
as is seen in Fig. 1. The number of connections also
varies greatly over time. Each connection has con-
stant value of 1 to 5 packets in the queue during their
life time. The delays for the services classes when
using constant weights are shown in Fig. 2. It is ob-
served that the delays remain quite constant because
the weights are constant. By using adaptive weights a
delay critical class used for e.g. real time traffic can
be favored with respect to delay. In the experiment
the parameters s
i
were chosen so that with adaptive
weights the gold class customers get less delay with
the expense of the other classes (Fig. 4). By adjusting
the penalty factors s
i
the relative delays between the
classes can be adjusted. The values of mean delays
Table 1: Mean delays of gold, silver and bronze class for
the constant and adaptive weight algorithms.
Mean delays [s] Gold Silver Bronze
Constant weights 0.1133 0.2642 0.7712
Adaptive weights 0.0804 0.4475 1.7155
PACKET SCHEDULING AND PRICING BASED ON INFLICTED DELAY
115

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
0
0.5
1
1.5
2
2.5
3
3.5
Time[s]
Delay[s]
Bronze
Silver
Gold
Figure 2: Constant weights - Evolution of the delay as a
function of time.
for the classes in both cases are seen In Table 1.
The adaptive weights are seen in Fig. 3 and the
total revenues for both versions of the algorithm is
seen in Fig. 5. Mean revenues in case of con-
stant weights was 5273.9 and in the case of optimal
adaptive weights 7297.0. The adaptive weights give
greater total revenue and smaller delay for the gold
class.
4 DISCUSSION
In this section, we discuss the algorithm from the
point of view of theory and experiments. Analytic
forms of the revenue and the weights, that allocate
traffic to the connections of different service classes
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
Bronze
Silver
Gold
w
i
Time[s]
Figure 3: Evolution of the weights w as a function of time.
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
0
0.5
1
1.5
2
2.5
3
3.5
Time[s]
Delay[s]
Bronze
Silver
Gold
Figure 4: Adaptive weights - Evolution of the delay as a
function of time.
were defined. The updating procedure is determinis-
tic and nonparametric i.e. it does not make any as-
sumptions of the statistical behavior of the traffic and
connections. Thus it is robust against the errors that
may occur from erroneous models. The algorithm
is unique and optimal, which has been theoretically
proved by Lagrangian optimization method. Closed
form solution makes the algorithm quite simple. By
changing the penalty factor s
i
of one class higher,
the delays in other classes are decreased. Because all
penalty factors s
i
are positive, all classes obtain ser-
vice in fair way. The method always optimizes the
operator’s revenue and by knowing what kind of traf-
fic is in different service classes the parameters can
be set so that the delay for delay critical traffic can
be maintained low enough. A call admission control
mechanism could also be implemented to assure def-
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
0
2000
4000
6000
8000
10000
12000
Time[s]
Revenue
Optimal
Constant
Figure 5: Evolution of the revenue R as a function of time.
ICE-B 2006 - INTERNATIONAL CONFERENCE ON E-BUSINESS
116

inite delay limits in cases the network load increases
too much. As the delays grow the operators revenue
increases, but it cannot increase to infinity in reality.
This is because when the buffers get full and pack-
ets start to drop, connections drop also at some point.
A penalty term for the operator is under study, which
would lower the price when there is too much delay.
5 CONCLUSION
In this paper an adaptive algorithm for optimizing
the network operator revenue and ensuring delay as
a Quality of Service (QoS) requirement was pre-
sented. The closed form algorithm was derived from
a revenue-based optimization problem. The pricing
of the connection is based on the delay that it in-
flicts on other connections. The customers that in-
duce most delay to the network by large amounts of
traffic are charged the most. In the experiments we
simulated the operation of the adaptive algorithm and
compared it with a constant weight version of the
same algorithm. The obtained results show that by
using the adaptive weights the delays can be adjusted
so that the users is different QoS classes are content.
With the constant weights, the delays cannot be con-
trolled. Also, the revenue is maximized while ensur-
ing that the customers delays stay small according to
the their class. The algorithm is deterministic and
non-parametric, and thus in practical environments it
is a competitive candidate due to its robustness. Fu-
ture work shall concentrate on expanding the idea to
several nodes with more QoS parameters.
REFERENCES
Bennett, J. C. R. and Zhang, H. (1996). WF
2
Q: worst-
case fair weighted fair queueing. In Proc. 15th Annual
Joint Conference of the IEEE Computer and Commu-
nications Societies (INFOCOM’96), volume 1, pages
120 – 128.
Demers, A., Keshav, S., and Shenker, S. (1989). Analy-
sis and simulation of a fair queuing algorithm. ACM
SIGCOMM Comput. Commun. Rev., 19(4):1–12.
Golestani, S. J. (1994). A self-clocked fair queueing scheme
for broadband applications. In Proc. 13th Annual Joint
Conference of the IEEE Computer and Communica-
tions Societies (INFOCOM’94), volume 2, pages 636
– 646.
Goyal, P., Vin, H. M., and Cheng, H. (1997). Start-time fair
queueing: a scheduling algorithm for integrated ser-
vices packet switching networks. IEEE/ACM Trans.
Networking, 5(5):690–704.
Guo, C. (2001). SRR: an O(1) time complexity packet
scheduler for flows in multi-service packet networks.
ACM SIGCOMM Comput. Commun. Rev., 31(4):211–
222.
Joutsensalo, J., Viinikainen, A., Hämäläinen, T., and Wik-
ström, M. (2005). Bandwidth allocation and pricing
for telecommunications network. In Proc. Next Gen-
eration Internet Networks (NGI’05), pages 165 – 172.
Kanhere, S. S. and Sethu, H. (2001). Fair, efficient and low-
latency packet scheduling using nested deficit round
robin. In Proc. IEEE Workshop on High Performance
Switching and Routing, pages 6 – 10.
Kanhere, S. S., Sethu, H., and Parekh, A. B. (2002). Fair
and efficient packet scheduling using elastic round
robin. IEEE Trans. Parallel Distrib. Syst., 13(3):324–
336.
Marosits, T., Molnár, S., and Sztrik, J. (2001). CAC algo-
rithm based on advanced round robin method for QoS
networks. In Proc. Sixth IEEE Symposium on Com-
puters and Communications, 2001, volume 2, pages
266 – 274.
Parekh, A. K. and Gallager, R. G. (1993). A general-
ized processor sharing approach to flow control in
integrated services networks: The single-node case.
IEEE/ACM Trans. Networking, 1(3):344–357.
Ramabhadran, S. and Pasquale, J. (2003). Stratified round
robin: A low complexity packet scheduler with band-
width fairness and bounded delay. In Proc. 2003 con-
ference on Applications, technologies, architectures,
and protocols for computer communications, pages
239 – 250. ACM Press.
Shreedhar, M. and Varghese, G. (1996). Efficient fair queu-
ing using deficit round-robin. IEEE/ACM Trans. Net-
working, 4(3):375–385.
Stiliadis, D. and Varma, A. (1998). Efficient fair queueing
algorithms for packet-switched networks. IEEE/ACM
Trans. Networking, 6(2):175–185.
Tsao, S.-C. and Lin, Y.-D. (2001). Pre-order deficit
round robin: a new scheduling algorithm for packet-
switched networks. Comput. Networks, 35(2-3):287–
305.
Viinikainen, A., Joutsensalo, J., Pääkkönen, M., and
Hämäläinen, T. (2004). Packet scheduling algorithm
with weight optimization. In Proc. International Con-
ference on E-business and Telecommunication Net-
works (ICETE’04), volume 2, pages 127 – 133.
Yuan, X. and Duan, Z. (2005). FRR: a proportional
and worst-case fair round robin scheduler. In Proc.
24th Annual Joint Conference of the IEEE Computer
and Communications Societies (INFOCOM’05), vol-
ume 2, pages 831– 842.
PACKET SCHEDULING AND PRICING BASED ON INFLICTED DELAY
117
