
NONLINEAR PRIMARY CORTICAL IMAGE
REPRESENTATION FOR JPEG 2000
Applying natural image statistics and visual perception to image compression
Roberto Valerio
UNIC, CNRS, 1 Avenue de la Terrasse, 91190 Gif-sur-Yvette, France
Rafael Navarro
ICMA, CSIC-Universidad de Zaragoza, Plaza San Francisco s/n, 50009 Zaragoza, Spain
Keywords: Nonlinear models of V1 neurons, Divisive normalization, Natural image statistics, Perceptual quality
metrics, JPEG 2000.
Abstract: In this paper, we present a nonlinear image representation scheme based on a statistically-derived divisive
normalization model of the information processing in the visual cortex. The input image is first decomposed
into a set of subbands at multiple scales and orientations using the Daubechies (9, 7) floating point filter
bank. This is followed by a nonlinear “divisive normalization” stage, in which each linear coefficient is
squared and then divided by a value computed from a small set of neighboring coefficients in space,
orientation and scale. This neighborhood is chosen to allow this nonlinear operation to be efficiently
inverted. The parameters of the normalization operation are optimized in order to maximize the statistical
independence of the normalized responses for natural images. Divisive normalization not only can be used
to describe the nonlinear response properties of neurons in visual cortex, but also yields image descriptors
more independent and relevant from a perceptual point of view. The resulting multiscale nonlinear image
representation permits an efficient coding of natural images and can be easily implemented in a lossy JPEG
2000 codec. In fact, the nonlinear image representation implements in an automatic way a more general
version of the point-wise extended masking approach proposed as an extension for visual optimisation in
JPEG 2000 Part 2. Compression results show that the nonlinear image representation yields a better rate-
distortion performance than the wavelet transform alone.
1 INTRODUCTION
The human visual system (HVS) plays a key role in
the final perceived quality of compressed images.
Therefore, it is desirable to take advantage of the
current knowledge of visual perception in a
compression system. The JPEG 2000 standard
includes various tools that permit to exploit some
properties of the HVS such as spatial frequency
sensitivity, color sensitivity, and visual masking
effects (Zeng et al., 2002). The visual tools sets in
JPEG 2000 are much richer than those in JPEG,
where only spatially-invariant frequency weighting
is used. As a result, visually optimized JPEG 2000
images usually have much better visual quality than
visually optimized JPEG images at the same bit
rates. Nevertheless, the visual optimization tools in
JPEG 2000 are still simplified versions of the latest
models of human visual processing.
In recent years, various authors have shown that
the nonlinear behavior of V1 neurons in primate
visual cortex can be modeled by including a gain
control stage, known as “divisive normalization”
(e.g. Heeger, 1992), after a linear filtering step. In
this nonlinear stage, the linear inputs are squared and
then divided by a weighted sum of squared
neighboring responses in space, orientation, and
scale, plus a regularizing constant. Divisive
normalization not only can be used to describe the
nonlinear response properties of neurons in visual
cortex, but also yields image descriptors more
relevant from a perceptual point of view (Foley,
1994). More recently, Simoncelli and co-workers
519
Valerio R. and Navarro R. (2006).
NONLINEAR PRIMARY CORTICAL IMAGE REPRESENTATION FOR JPEG 2000 - Applying natural image statistics and visual perception to image
compression.
In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 519-522
DOI: 10.5220/0001377205190522
Copyright
c
SciTePress

(e.g. Schwartz and Simoncelli, 2001) presented a
statistically-derived divisive normalization model.
They demonstrated its utility to characterize the
nonlinear response properties of neurons in sensory
systems, and thus that early neural processing is well
matched to the statistical properties of the stimuli. In
addition, they showed empirically that the divisive
normalization model strongly reduces pairwise
statistical dependences between responses.
In this paper, we describe a nonlinear image
representation scheme (similar to Valerio et al.,
2003) based on a statistically-derived divisive
normalization model of V1 neurons. This scheme
could be useful in a lossy JPEG 2000 codec. Starting
with a 9/7 Daubechies wavelet decomposition, we
normalize each coefficient by a value computed
from a neighborhood. This neighborhood is
suboptimal for dependency reduction, but allows the
transform to be easily inverted. We describe the
empirical optimization of the transform parameters,
and demonstrate that the redundancy in the resulting
coefficients is substantially less than that of the
original linear ones. Compression results show that
the nonlinear representation can improve the
perceptual quality of compressed images.
2 NONLINEAR IMAGE
REPRESENTATION SCHEME
The scheme used here consists of a linear wavelet
decomposition followed by a nonlinear divisive
normalization stage.
2.1 Linear Stage
The linear stage is an approximately orthogonal
four-level wavelet decomposition based on the
Daubechies (9, 7) floating point filter bank. The 9/7
transform is nonreversible and real-to-real, and is
one of the two specific wavelet transforms supported
by the baseline JPEG 2000 codec (the other one is
the 5/3 transform, which is reversible, integer-to-
integer and nonlinear). Lacking the reversible
property, the 9/7 transform can only be used for
lossy coding.
2.2 Nonlinear Stage
The nonlinear stage consists basically of a divisive
normalization. In this stage, the responses of the
previous linear filtering stage, c
i
, are squared and
then divided by a weighted sum of squared
neighboring responses in space, orientation, and
scale,
}{
2
j
c
, plus a positive constant,
2
i
d
:
∑
+
⋅
=
j
jiji
ii
i
ced
ccsign
r
22
2
)(
(1)
Eq. 1 is similar to models of cortical neuron
responses but has the advantage that preserves sign
information. The parameters,
2
i
d
and {e
ij
}, of the
divisive normalization are fixed to the following
values (Schwartz and Simoncelli, 2001):
2
i
d
=
2
i
a
,
e
ij
= b
ij
(i ≠ j) and e
ii
= 0, where
2
i
a
and b
ij
(i ≠ j) are
the parameters of a Gaussian model for the
conditional probability . This choice of
parameters yields approximately the minimum
mutual information (MI), or equivalently minimizes
statistical dependence, between normalized
responses for a set of natural images (Valerio and
Navarro, 2003). In practice, we fix the parameters,
2
i
d
and {e
ij
}, of the divisive normalization for each
subband by using maximum-likelihood (ML)
estimation with a set of natural images (“Boats”,
“Elaine”, “Goldhill”, “Lena”, “Peppers”, and
“Sailboat” in our case). Numerical measures of
statistical dependence in terms of MI for the 6
512x512 B&W images with 8 bpp in the “training
set” show that divisive normalization decreases MI,
with most values much closer to zero. So, for
example, the mean value of MI between two
neighboring wavelet coefficients, c
i
and c
j
(c
j
is the
right down neighbor of c
i
), from the lowest scale
vertical subband is 0.10, whereas between the
corresponding normalized coefficients, r
i
and r
j
, is
only 0.04.
A key feature of the nonlinear stage is the
particular neighborhood considered in Eq. 1. We
consider 12 coefficients {c
j
} (j ≠ i) adjacent to c
i
along the four dimensions (9 in a square box in the
2D space, plus 2 neighbors in orientation and 1 in
spatial frequency). All neighbors belong to higher
levels of the linear pyramid. This permits to invert
the nonlinear transform very easily level by level (to
recover one level of the linear pyramid we obtain the
normalizing values from levels already recovered
and multiply them by the corresponding nonlinear
coefficients). Obviously, in order to invert the
nonlinear transform we need the low-pass residue of
the linear decomposition. More details can be found
in Valerio et al. (2003).
}){|(
2
ji
ccp
VISAPP 2006 - IMAGE ANALYSIS
520

3 PERCEPTUAL METRIC
From the nonlinear image representation it is
possible to define a perceptual image distortion
metric similar to that proposed by Teo and Heeger
(1994). For that, we simply add an error pooling
stage. This computes a Minkowski sum with
exponent 2 of the differences
i
rΔ
(multiplied by
constants k
i
that adjust the overall gain) between the
nonlinear outputs from the reference image and
those from the distorted image (Valerio et al., 2004):
∑
Δ⋅=Δ
i
ii
rkr
2
2
(2)
This perceptual metric has two main differences
with respect to that by Teo and Heeger (1994). First,
the divisive normalization considers not only
neighbouring responses in orientation but also in
position, and scale. Second, the parameters of the
divisive normalization are adapted to natural image
statistics instead of being fixed exclusively to fit
psychophysical data.
4 CODING RESULTS
In order to compare the coding efficiency of the 9/7
transform alone and our nonlinear transform (the 9/7
transform plus the divisive normalization), we have
conducted a series of compression experiments with
a simplified JPEG 2000 codec. Basically, the coding
is as follows. First, the input image is preprocessed
(the nominal dynamic range of the samples is
adjusted by subtracting a bias of 2
P-1
, where P is the
number of bits per sample, from each of the samples
values). Then, the intracomponent transform takes
place. This can be the 9/7 transform or our nonlinear
transform. In both cases, we use the implementation
of the 9/7 transform in the JasPer software (Adams
and Kossentini, 2000). After quantization is
performed in the encoder (we fix the quantizer step
size at one, that is, there is no quantization), tier-1
coding takes place.
In the tier-1 coder, each subband is partitioned
into code blocks (the code block size is 64x64), and
each of the code blocks is independently coded. The
coding is performed using a bit-plane coder. There is
only one coding pass per bit plane and the samples
are scanned in a fixed order as follows. The code
block is partitioned into horizontal stripes, each
having a nominal height of four samples. The stripes
are scanned from top to bottom. Within a stripe,
columns are scanned from left to right. Within a
column, samples are scanned from top to bottom.
The sign of each sample is coded with a single
binary symbol right before its most significant bit.
The bit-plane encoding process generates a sequence
of symbols that are entropy coded. For the purposes
of entropy coding, a simple adaptive binary
arithmetic coder is used. All of the coding passes of
a code block form a single codeword (per-segment
termination).
Tier-1 coding is followed by tier-2 coding, in
which the coding pass information is packaged.
Each packet consists of two parts: header and body.
The header indicates which coding passes are
included in the packet, while the body contains the
actual coding pass data. The coding passes included
in the packet are always the most significant ones
and we use a fixed-point representation with 13 bits
after the decimal point, so that we only need to store
the maximum number of bit planes of each code
block.
In tier-2 coding, rate control is achieved through
the selection of the subset of coding passes to
include in the code stream. The encoder knows the
contribution that each coding pass makes to the rate,
and can also calculate the distortion reduction
associated with each coding pass. Using this
information, the encoder can then include the coding
passes in order of decreasing distortion reduction per
unit rate until the bit budget has been exhausted.
This approach is very flexible and permits the use of
different distortion metrics.
Figs. 1 and 2 show some compression results
with the codec described above. The input image is
in both figures a 128x128 patch (this is for
simplicity, since if we use this image size there is
only one code block per subband) of the 8 bpp
“Baboon” image, and we consider only the lowest
scale vertical subband. The results are very different
depending on the distortion metric used. As we can
see in Fig. 1, if we use the classical mean squared
error (MSE) as distortion metric (note that the MSE
is not very well matched to perceived visual quality)
the 9/7 transform yields better results than the
nonlinear transform. However, the nonlinear
transform yields better perceptual quality than the
9/7 transform (see Fig. 2).
In Fig. 3 we can see that the MSE, or
equivalently the peak signal-to-noise ratio (PSNR),
is not very well matched to perceived visual quality.
So, despite their very different MSE (the PSNR
corresponding to the 9/7 transform is more than 10
dB greater than that of the nonlinear transform), the
two decoded images showed in the figure are almost
visually indistinguishable.
NONLINEAR PRIMARY CORTICAL IMAGE REPRESENTATION FOR JPEG 2000 - Applying natural image statistics
and visual perception to image compression
521
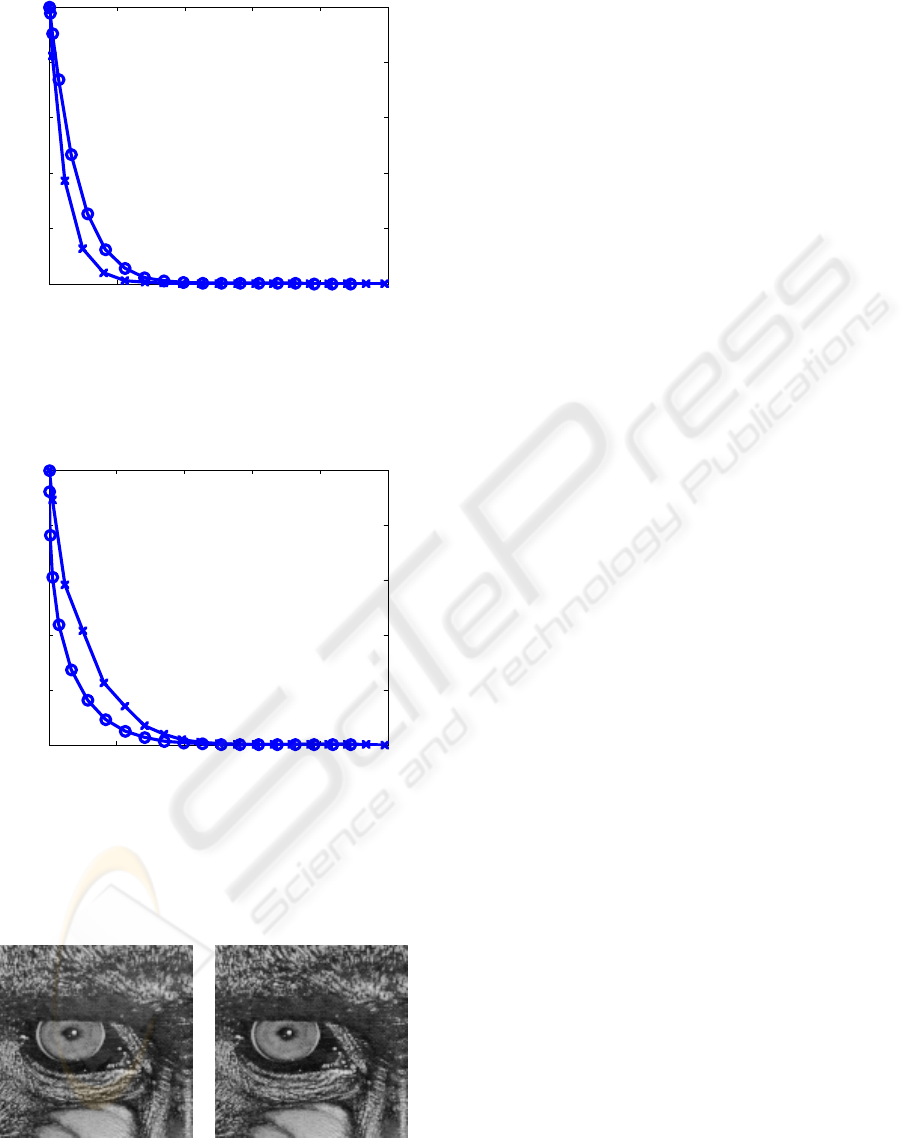
0 2000 4000 6000 8000 10000
0
0.2
0.4
0.6
0.8
1
Size (bytes)
Relative MSE
Figure 1: Relative MSE (1 denotes the MSE when any bit
plane of the considered subband is coded) as a function of
the number of bytes at the output of the encoder, for the
9/7 transform (‘x’) and the nonlinear transform (‘o’).
0 2000 4000 6000 8000 10000
0
0.2
0.4
0.6
0.8
1
Size (bytes)
Relative perceptual error
Figure 2: Relative perceptual error (1 denotes the
perceptual error when any bit plane of the considered
subband is coded) as a function of the number of bytes at
the output of the encoder, for the 9/7 transform (‘x’) and
the nonlinear transform (‘o’).
Figure 3: Decoded images corresponding to the 9/7
transform (left) and the nonlinear transform (right), when
using 7 and 10 bit planes (3395 and 3401 bytes)
respectively to code the considered subband.
5 SUMMARY AND
CONCLUSIONS
We have presented a nonlinear image representation
scheme based on a statistically-derived model of
information processing in the visual cortex. The key
feature of this image representation scheme is that
the resulting coefficients are almost statistically
independent, much more than those of the
orthogonal linear transforms (these cannot eliminate
higher-order dependencies). Such representation has
been also shown relevant to human perception.
This nonlinear image representation could be
very useful in a lossy JPEG 2000 codec. A similar
approach has been proposed in JPEG 2000 Part 2 as
an extension for visual optimisation and also similar
schemes have already been used successfully in
image compression applications. Compression
results with a simplified JPEG 2000 codec show that
the nonlinear image representation yields better
perceptual quality than the 9/7 wavelet transform
alone.
REFERENCES
Adams, M. D., and Kossentini, F., 2000. JasPer: A
software-based JPEG-2000 codec implementation.
Proc. of ICIP, 2: 53-56.
Foley, J. M., 1994. Human luminance pattern
mechanisms: Masking experiments require a new
model. Journal of the Optical Society of America A,
11: 1710-1719.
Heeger, D. J., 1992. Normalization of cell responses in cat
striate cortex. Visual Neuroscience, 9: 181-198.
Schwartz, O., and Simoncelli, E. P., 2001. Natural signal
statistics and sensory gain control. Nature
neuroscience, 4(8): 819-825.
Teo, P., and Heeger, D., 1994. Perceptual image
distortion. Proc. of ICIP, 2: 982-986.
Valerio, R., and Navarro, R., 2003. Input-output statistical
independence in divisive normalization models of V1
neurons. Network: Computation in Neural Systems,
14: 733-745.
Valerio, R., Simoncelli, E. P., and Navarro, R., 2003.
Directly invertible nonlinear divisive normalization
pyramid for image representation. In Lecture Notes in
Computer Science, Springer, 2849: 331-340.
Valerio, R., Navarro, R., and ter Haar Romeny, B. M.,
2004. Perceptual image distortion metric based on a
statistically-derived divisive normalization model. In
Early Cognitive Vision Workshop, Isle of Skye, UK.
Zeng, W., Daly, S., and Lei, S., 2002. An overview of the
visual optimization tools in JPEG 2000. Signal
Processing: Image Communication Journal, 17(1):
85-104.
VISAPP 2006 - IMAGE ANALYSIS
522
