
SYNTHESIZING FACE IMAGES BY IRIS REPLACEMENT:
STRABISMUS SIMULATION
Xiaoyi Jiang, Swenja Rothaus, Kai Rothaus
Department of Mathematics and Computer Science, University of M
¨
unster, Germany
Einsteinstrasse 62, D-48149 M
¨
unster, Germany
Daniel Mojon
Department of Strabismology and Neuro-Ophthalmology, Kantonsspital St.Gallen , Switzerland
Kantonsspital St.Gallen, CH-9007 St.Gallen, Switzerland
Keywords:
strabismus simulation, contour detection, dynamic programming, image inpainting.
Abstract:
In this paper we consider a class of face image processing operations, in which we change the position of
the iris. In particular, we present a novel technique for synthesizing strabismic face images from a normal
frontal face image. This image synthesis is needed for conducting studies in psychosocial and vocational
implications of strabismus and strabismus surgery and we are not aware of any previous work for this purpose.
The experimental results demonstrate the potential of our approach. The algorithm presented in this paper
provides the basis for two related tasks of correction of strabismic face images and gaze direction.
1 INTRODUCTION
An important application of computer vision is intelli-
gent image editing which allows users to easily mod-
ify an image with minimum amount of manual work.
Often we are faced with the need to edit/process hu-
man face images, which is in fact of considerable im-
portance in such areas like home imaging, human-
machine interface, and biometrics (Yan, 2001). An
example with huge commercial potential is to remove
red eyes commonly seen in images taken with a flash
(Smolka et al., 2003). Some previous works (Ghent
and McDonald, 2005; Liu et al., 2001) propose ap-
proaches to synthesizing facial expressions. Genera-
tion of eye appearance variations is used in (Kamgar-
Parsi et al., 2003) to artificially enlarge the training
set for person authentication purpose. As a matter
of fact, simulation of facial expressions can be of in-
terest in this context as well, although not consid-
ered in (Kamgar-Parsi et al., 2003). In (Hwang and
Lee, 2003) an approach is proposed to reconstruct
partially damaged face images. Other facial image
editing/processing tasks include eyeglasses detection
and removal (Jiang et al., 2000; Park et al., 2005; Wu
et al., 2004), simulation of aging effects (Lanitis et al.,
2002), facial weight change simulation (Danino et al.,
2004), and caricature generation (Chiang et al., 2004).
The current work is related to a class of face image
processing operations, in which the position of the iris
is changed. Several applications belong to this prob-
Figure 1: Picture of a strabismus patient.
lem class:
• synthesis of strabismic face images
• correction of strabismic face images (opposite to
the first task) with plastic surgery applications
• correction of gaze direction (for editing pho-
tographs etc.)
The emphasis of this paper is the synthesis of stra-
bismic face images; see Section 2 for the motiva-
tion of this task. We will present a novel algorithm
for synthesizing strabismic face images of an arbi-
trary angle (Section 3) and show experimental re-
sults (Section 4). In addition we will discuss the ex-
tensions/modifications for the two other related tasks
(Section 5).
41
Jiang X., Rothaus S., Rothaus K. and Mojon D. (2006).
SYNTHESIZING FACE IMAGES BY IRIS REPLACEMENT: STRABISMUS SIMULATION.
In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 41-47
DOI: 10.5220/0001376900410047
Copyright
c
SciTePress

2 MOTIVATION
Synthesizing strabismic face images, each of a dif-
ferent angle, based on a normal frontal face image
is needed for conducting studies in psychosocial and
vocational implications of strabismus and strabismus
surgery.
The presence of strabismus precludes normal eye
contact, which is a significant disability in social and
vocational settings; see Figure 1 for an example pic-
ture
1
. Strabismus can have a negative impact on an
individual’s employment opportunity, school perfor-
mance, and self-perception. The presence of strabis-
mus on a resume photograph, when compared to the
same resume with the photograph depicting straight
eyes, resulted in significantly lower ratings of the ap-
plicant’s attentiveness, competency, emotional stabil-
ity, intelligence, leadership abilities, communication
and organizational skills, sincerity and employability.
A recent study (Coats et al., 2000) for instance indi-
cates that large-angle horizontal strabismus appeared
to be vocationally significant particularly for female
applicants, reducing their ability to obtain employ-
ment. Currently, we are conducting a new, larger-
scale study in this context, in which strabismic images
of different angles of the same person are needed. In
this study a large number of persons is involved.
One possibility of synthesizing strabismic face im-
ages lies in manual image editing using standard im-
age processing packages (Coats et al., 2000). Al-
ternatively, one may ask a person to simulate differ-
ent strabismic angles. Both methods are tedious and
time-consuming, thus not applicable if many face im-
ages are needed. The latter approach has an additional
problem that it is hardly possible for a person to pre-
cisely simulate a particular desired angle.
In this work we present a novel algorithm for syn-
thesizing strabismic face images of an arbitrary an-
gle. We are not aware of any previous work for this
purpose, although there are several works on synthe-
sizing eyes, for example for automatic eye movement
model in computer graphics (Deng et al., 2005) and
generation of eye appearance variations to enhance
the training set for person authentication (Kamgar-
Parsi et al., 2003).
3 SYNTHESIZING STRABISMIC
FACE IMAGES
The input is a frontal face image. Our algorithm con-
sists of the following main steps:
1
The reader can download the PDF file of this
paper with all color figures at http://www.math.uni-
muenster.de/u/xjiang/papers/VISAPP2006.pdf.
(a) (b) (c)
(d) (e) (f)
Figure 2: Main steps of algorithm: (a) (part of) input image;
(b) detected contour of iris and reflection point; (c) removal
of iris; (d) detected eye contour; (e) rotated eye; (f) embed-
ded reflection point. The final result is given in (f).
• detection of the contour of the iris and the reflection
point
• removal of the iris
• detection of the contour of the eye
• rotation of the eye, i.e. re-insertion of the iris
• placement of the reflection point
The whole procedure of processing an input face im-
age is illustrated in Figure 2. The algorithmic details
are given in the following subsections.
3.1 Contour Detection by Dynamic
Programming
There are totally three instances of contour detection
in our task: the iris, the reflection point and the eye;
see Figure 2(b) and (d). Several approaches have been
proposed to deal with some of these detection prob-
lems (Lanitis et al., 1997; Yuille et al., 1992). In this
work we take a unified framework of dynamic pro-
gramming to detect all three contours.
Dynamic programming is a very efficient way of
finding an optimal path in a matrix of weights with
an unknown start point in the first row and an un-
known end point in the last row (Dawant and Zijden-
bos, 2000; Sonka et al., 1999). Among all possible
paths from top to bottom this optimal path minimizes
(or maximizes) the sum of weights of all elements on
the path. If the matrix represents the edge magnitude,
then the optimal path found by the dynamic program-
ming simply means the best contour which maximizes
the sum of edge magnitudes. Let S denote the weight
matrix. The optimal path is computed by means of a
cumulative weight matrix C in a row-column manner.
VISAPP 2006 - IMAGE FORMATION AND PROCESSING
42

The first row of C is initialized by the corresponding
values from S. Starting from the second row, the cu-
mulative weight at position (i, j) is computed for each
column as:
C(i, j) = min
n∈N(i,j)
[C(n)+T (n, (i, j)) + S(i, j)]
where N(i, j) is the set of possible predecessors
of (i, j) in the last row i − 1. In the case of 8-
neighborhood, N(i, j) is usually set to be {(i −1,j−
1), (i−1,j), (i−1,j+1)}. T (n, (i, j)) represents the
transition weight from the predecessor n to the cur-
rent position (i, j). In addition to computing C(i, j),
a pointer is set to the predecessor n that achieves the
minimum among all predecessors in N (i, j). To de-
termine the optimal path we follow the pointers from
the last row to first row, starting from the position in
the last row of C with the maximal value.
The standard dynamic programming can be easily
extended to handle closed contours. For this purpose
we need a point p in the interior of the contour. Then,
a polar transformation with p being the central point
brings the original image into a matrix, in which a
closed contour becomes a contour from top to bot-
tom afterwards. The optimal path is computed in this
polar space and mapped back to the original image.
Note that this approach works well for all star-shaped
contours including convex contours as a special case.
Currently, we ask the user to mark a single point
within the reflection point (although this part could be
automated as well). The contours of the iris and the
reflection point differ in the corresponding edge types.
In the polar transformed image of the eye, the con-
tour of the reflection point is lying on an edge from
bright to dark and in contrast the contour of the iris
is lying on an edge from dark to bright. The weight
matrix, which is used for the dynamic programming
algorithm to detect the contours, is computed by fi-
nite backward differences (reflection point) and finite
forward (iris), respectively.
For the iris contour an additional step is introduced
to produce a smoother contour. Based on the points
on the detected iris contour we apply the method of
least median of squares (Roth and Levine, 1993) to
obtain a circle which will be used in the subsequent
operations.
The eye contour is detected after the iris is re-
moved; see Figure 2(c) and Section 3.2. In princi-
ple exactly the same procedure as used for detecting
the contour of the iris and the reflection point could
be applied here as well. However, based on the spe-
cial structure of the eye part we combine two different
sources of edge magnitude to enhance the detection
quality. The first source is the standard edge mag-
nitude e
image
; see Figure 3(a) for an example where
the edge magnitude was computed by the Canny oper-
ator. The second source results from an edge magni-
(a) (b) (c)
Figure 3: Combined edge magnitude for detecting the eye
contour: (a) e
image
; (b) e
diff
; (c) combination.
tude computation e
diff
in an image of difference be-
tween the red and the green channel; see Figure 3(b).
These two sources are combined by a weighted sum
e
image
+3· e
diff
. The result given in Figure 3(c)
shows a more uniform appearance of the eye contour
in this combined edge magnitude. This representa-
tion is then transformed into the polar space in Fig-
ure 4(a) and the application of dynamic programming
finds the optimal contour in Figure 4(b). Mapping it
back to the original image, we finally obtain the eye
contour as shown in Figure 2(d).
3.2 Iris Removal by Inpainting
For simulating strabismus the iris has to be removed
and placed at a new position within the eye contour
according to the desired angle. At least part of the
original iris area thus must be filled with new content.
The iris removal should be done with care. Typi-
cally, the eyelashes partially interlay with the iris so
that a straightforward removal and subsequently fill-
ing this area by the eye background would produce
unnatural appearance in the eyelash (which was ac-
tually observed in the experiments done in the initial
phase of this work). Instead, we have to fill the miss-
ing background and continue the missing eyelashes in
a natural way simultaneously.
We propose to apply image inpainting techniques
for this purpose. In our current implementation the in-
painting algorithm reported in (Criminisi et al., 2000)
is used, due to its advantage of performing texture
synthesis under full consideration of the constraints
imposed by linear structures. Let Ω be the region of
the removed iris to be filled and δΩ its boundary (the
fill front). For every point p ∈ δΩ a term called prior-
ity is computed:
P (p)=C(p)D(p)
where C(p) is the confidence term and D(p) the data
term and they are defined as follows:
C(p)=
q∈ψ
p
∩(I−Ω)
C(q)
| ψ
p
|
,D(p)=
|∇I
⊥
p
· n
p
|
α
where I represents the whole image, ψ
p
a small
square neighborhood of p, n
p
the normal to the
SYNTHESIZING FACE IMAGES BY IRIS REPLACEMENT - Strabismus Simulation
43
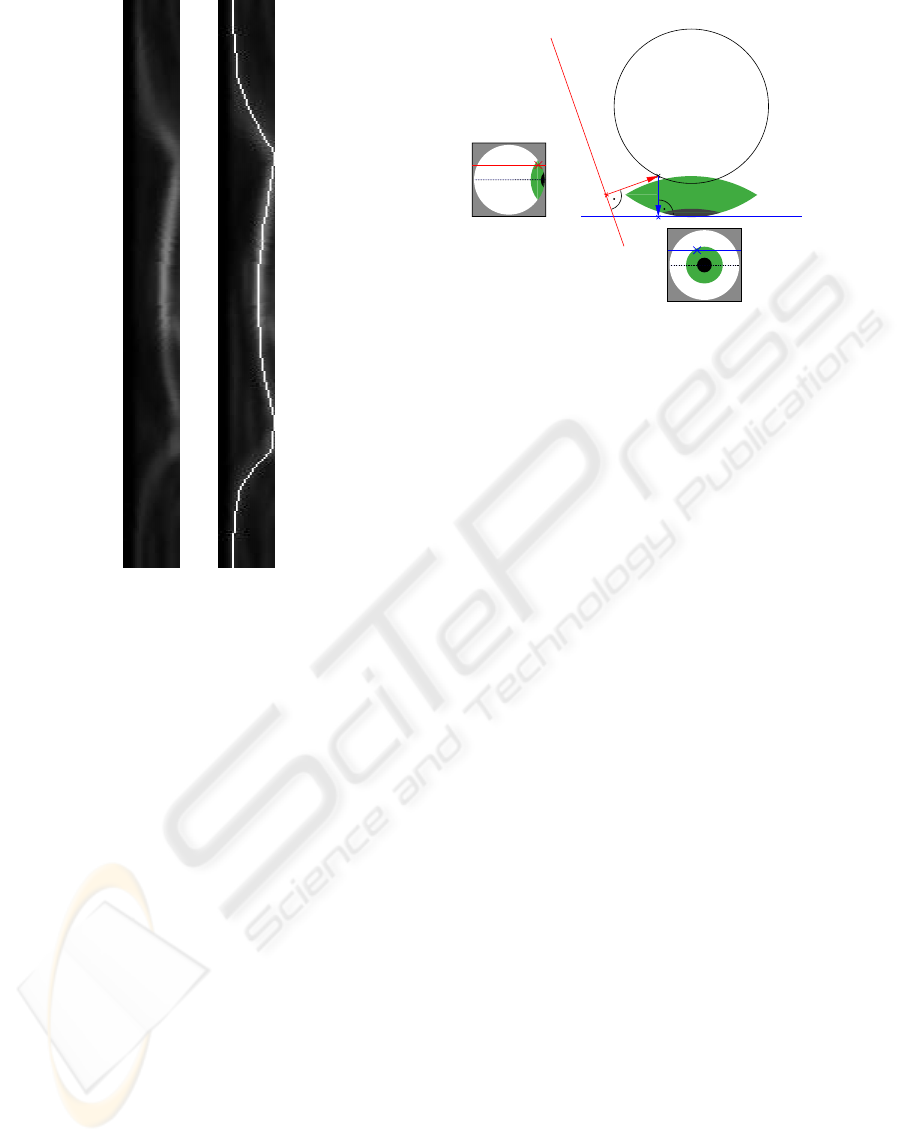
(a) (b)
Figure 4: Polar space for contour detection: (a) polar space;
(b) optimal path.
boundary δΩ, ∇I
⊥
p
the greyscale isophote at point p,
and α a normalization factor. The confidence value
reflects our confidence in the pixel value. The pri-
ority value determines the order in which Ω is filled.
During initialization the function C is set to C(p)=
0 ∀p ∈ Ω and C(p)=1∀p ∈I−Ω.
The algorithm iterates the following steps until Ω
becomes empty:
1. Identify the fill front δΩ.
2. Compute the priorities P (p), ∀p ∈ δΩ.
3. Find ˆp ∈ δΩ with the maximum priority.
4. Find the pixel ˆq ∈I−Ω most similar to ˆp (in terms
of their neighborhood ψ
ˆp
and ψ
ˆq
).
5. Copy image data from ψ
ˆq
to the unfilled part of ψ
ˆp
,
i.e., ψ
ˆp
∩ Ω.
6. Update the confidence values of newly filled pixels.
The use of this inpainting algorithm allows us to fill
the open area caused by eye rotation, in particularly
the continuation of eyelashes.
3.3 Eye Rotation
Instead of rotating the eye directly, we virtually com-
pute an image on a destination plane, which has the
~
p
d
estination image plane
eyeball
p’
p
source image pla
ne
Figure 5: Eye rotation.
desired angle (as specified by the user) with the source
image plane, see Figure 5. The intensity at p
is de-
termined by tracing the ray to the eyeball and then to
position p in the source image plane. Finally, the iris
part of the virtual image is embed to the prepared eye
image. Note that this step is subject to a clipping op-
eration such that rotated iris remains within the eye
contour.
3.4 Placement of Reflection Point
Despite of strabismus the reflection point should re-
main unchanged. Therefore, as the last operation the
detected reflection point is embedded exactly at the
same coordinates as in the input image.
Due to the same reason one additional operation is
actually performed before the eye rotation described
in Section 3.3. The reflection point has to be removed
from the source image. This is done by the same in-
painting algorithm as for the purpose of iris removal.
4 EXPERIMENTAL RESULTS
Figure 6 shows the results for four different horizontal
angles. They demonstrate that our approach is able to
synthesize strabismic face images of natural looking
(although persons not familiar with watching this kind
of faces may find them inherently unnatural). This
has been confirmed by experienced ophthalmologists
in daily contacts with strabismus patients. In addition
to the overall impression of the resulting images, we
are particularly able to reasonably fill the open area
caused by the eye rotation by inpainting techniques.
Two additional synthesized images are shown in in
Figure 7. Finally, Figure 8 demonstrates a detailed
view of the eye part for four different face images.
For each person the original face image on the top is
VISAPP 2006 - IMAGE FORMATION AND PROCESSING
44

Figure 6: Top: Input image. Middle: 20
o
and 40
o
to the
right. Bottom: 20
o
and 40
o
to the left. Only the right eye of
the person is processed.
followed by two strabismic images with 20
o
and 40
o
to the right and two strabismic images with 20
o
and
40
o
to the left.
Basically, the same algorithm could be applied to
simulate strabismus of vertical angles as well. Such
an example can be observed in Figure 9. One poten-
tial difficulty here is that we may need part of the iris
that is not visible in the original face image. Imagine,
for instance, a vertical angle in the opposite direction
as in Figure 9. In this case the bottom part of the iris
has to be artificially completed before it can be em-
bedded to the prepared eye background.
Figure 7: Two additional results.
5 EXTENSIONS TO RELATED
TASKS
Correction of strabismic face images is of great in-
terest in plastic surgery applications. This gives the
patient an approximate post-operation look of stra-
bismus surgery in the pre-operation phase. There are
several differences to synthesizing strabismic face im-
ages. The reflection point may not be in the iris any-
more. Similar to synthesizing vertical strabismus, the
iris in the input image is only partially visible and thus
has to be completed in some way. One possibility is
to make use the information from the other eye since
many patients suffer from strabismus in only one eye.
The task of gaze direction correction is related to cor-
rection of strabismic face images and the discussions
above apply here as well. Currently, we are realizing
these extensions for these two additional applications
related to synthesizing strabismic face images.
6 CONCLUSION
In this paper we have considered a class of face im-
age processing operations, in which we change the
position of the iris. In particular, a novel technique
for synthesizing strabismic face images from a nor-
mal frontal face image was presented. Compared to
manual image editing typically practiced so far, an
automatic method like ours allows researchers to con-
duct studies in psychosocial and vocational implica-
tions of strabismus and strabismus surgery by means
of a large number of strabismic face images of many
persons with little efforts. The experimental results
demonstrated the potential of our approach. Even in
the worst case where the resulting strabismic face im-
ages suffer from some (local) imperfection, a manual
correction can be done with reasonable costs and thus
such an automatic approach remains advantageous.
Note that currently, we ask the user to mark a single
SYNTHESIZING FACE IMAGES BY IRIS REPLACEMENT - Strabismus Simulation
45

Figure 8: Detailed views of four face images.
Figure 9: Strabismic image with a vertical angle.
point within the reflection point. This is in line with
many other face image editing/processing algorithms,
in which some minimum degree of human interaction
is needed. In typical applications of these editing op-
erations this is no real burden and can be safely toler-
ated.
The current state of our algorithm can be improved
in several ways. We still have some difficulties in gen-
erating vertical strabismic face images. Also, we need
the extensions discussed in the last section for the cor-
rection of strabismic face images and gaze direction.
REFERENCES
Chiang, P., Liao, W.-H., and Li, T.-Y. (2004). Automatic
caricature generation by analyzing facial features. In
Proc. of Asian Conf. on Computer Vision, Jeju Island,
Korea.
Coats, D., Paysse, E., Towler, A., and Dipboye, R. (2000).
Impact of large angle horizontal strabismus on ability
to obtain employment. Ophthalmology, 107(2):402–
405.
Criminisi, A., P
´
erez, P., and Toyama, K. (2000). Region fill-
ing and object removal by exemplar-based image in-
painting. IEEE Trans. Image Processing, 13(9):1200–
1212.
Danino, U., Kiryati, N., and Furst, M. (2004). Algo-
rithm for facial weight change. In Proc. of 11th
IEEE Int. Conf. Electronics, Circuits and Systems
(ICECS’2004), pages 318–321.
Dawant, B. and Zijdenbos, A. (2000). Image segmentation.
In Sonka, M. and Fitzpatrick, J., editors, Handbook of
Medical Imaging, Volume 2. Medical Image Process-
ing and Analysis, pages 71–127. SPIE Press.
Deng, Z., Lewis, J., and Neumann, U. (2005). Automated
eye motion using texture synthesis. IEEE Computer
Graphics and Applications, 25(2):24–30.
Ghent, J. and McDonald, J. (2005). Photo-realistic facial
expression synthesis. Image and Vision Computing,
23:1041–1050.
Hwang, B.-W. and Lee, S.-W. (2003). Reconstruction of
partially damaged face images based on a morphable
face model. IEEE Trans. PAMI, 25(3):365–372.
Jiang, X., Binkert, M., Achermann, B., and Bunke, H.
(2000). Towards detection of glasses in facial images.
Pattern Analysis and Applications, 3(1):9–18.
Kamgar-Parsi, B., Kamgar-Parsi, B., and Jain, A. (2003).
Synthetic eyes. In Kittler, J. and Nixon, M., editors,
Audio- and Video-Based Biometric Person Authenti-
cation, pages 412–420. Springer-Verlag.
Lanitis, A., Taylor, C., and Cootes, T. (1997). Automatic
interpretation and coding of face images using flexible
models. IEEE Trans. PAMI, 19(7):743–756.
Lanitis, A., Taylor, C., and Cootes, T. (2002). Toward au-
tomatic simulation of aging effects on face images.
IEEE Trans. PAMI, 24:442–455.
Liu, Z., Shan, Y., and Zhang, Y. (2001). Expressive ex-
pression mapping with ratio images. In Proc. of SIG-
GRAPH, pages 271–276.
Park, J., Oh, Y., Ahn, S., and Lee, S. (2005). Glasses re-
moval from facial image using recursive error com-
pensation. IEEE Trans. PAMI, 27(5):805–811.
VISAPP 2006 - IMAGE FORMATION AND PROCESSING
46

Roth, G. and Levine, M. (1993). Extracting geometric prim-
itives. CVGIP: Image Understanding, 58(1):1–22.
Smolka, B., Czubin, K., Hardeberg, J., Plataniotis, K.,
Szczepanski, M., and Wojciechowski, K. (2003).
Towards automatic redeye effect removal. Pattern
Recognition Letters, 24(11):1767–1785.
Sonka, M., Hlavac, V., and Boyle, R. (1999). Image
Processing, Analysis, and Machine Vision. PWS Pub-
lishing, 2nd edition edition.
Wu, C., Liu, C., Shum, H.-Y., Xu, Y.-Q., and Zhang, Z.
(2004). Automatic eyeglasses removal from face im-
ages. IEEE Trans. PAMI, 26(3):322–336.
Yan, H. (2001). Human face image processing tech-
niques. International Journal of Image and Graphics,
1(2):197–215.
Yuille, A., Hallinan, P., and Cohen, D. (1992). Feature ex-
traction from faces using deformable templates. Inter-
national Journal of Computer Vision, 8(2):99–111.
SYNTHESIZING FACE IMAGES BY IRIS REPLACEMENT - Strabismus Simulation
47
