
ADAPTIVE STACK FILTERS IN SPECKLED IMAGERY
Mar
´
ıa E. Buemi, Marta E. Mejail, Julio C. Jacobo, Mar
´
ıa J. Gambini
Departamento de Computaci
´
on. Facultad de Ciencias Exactas y Naturales. Universidad de Buenos Aires
Pabell
´
on I. Ciudad Universitaria.1428 Buenos Aires. Rep
´
ublica Argentina
Keywords:
Stack filter, sinthetic aperture radar, speckle, classification.
Abstract:
Stack filters are a special case of non-linear filters. They have a good performance for filtering images with
different types of noise while preserving edges and details. A stack filter decomposes an input image into
several binary images according to a set of thresholds. Each binary image is filtered by using a boolean
function. Adaptive stack filters are optimized filters that compute a boolean function by using a corrupted
image and ideal image without noise. In this work the behaviour of an adaptive stack filter is evaluated for the
classification of synthetic apreture radar (SAR) images, which are affected by speckle noise. With this aim
it is carried out a Monte Carlo experiment in which simulated images are generated and then filtered with a
stack filter trained with one of them. The results of their maximum likelihood classification are evaluated and
then are compared with the results of classifying the images without previous filtering.
1 INTRODUCTION
Stack filters are a special case of non-linear filters.
They have a good performance for filtering images
with different types of noise while preserving edges
and details. These filters consist of a decomposition
by thresholds of an input signal obtaining a binary sig-
nal for each threshold. Each binary signal is filtered
using a sliding window. Stack filters can be gener-
ated using an adaptive algorithm, in such a way that
the so-called stacking property holds. The stack filter
design method used in this work is based on an algo-
rithm proposed by Yoo et al. (Yoo et al., 1999). In
this paper we study the application of this type of fil-
ter to Synthetic Aperture Radar (SAR) images. SAR
images (Goodman, 1976) and (Oliver and Quegan,
1998) are generated by a coherent illumination sys-
tem and are affected by the coherent interference of
the signal backscatter by the elements on the terrain.
This interference causes fluctuations of the detected
intensity which varies from pixel to pixel. This ef-
fect is called speckle noise. Speckle noise, unlike
noise in optical images, is neither Gaussian nor ad-
ditive; it follows other distributions and is multiplica-
tive. Due to all of this it is not possible to treat these
images using the classical techniques appropiate for
optical image processing. The analysis of this type
of images has been treated in the literature using sev-
eral statistical methods, see for example (Frery et al.,
1999), (Mejail et al., 2001), (Mejail et al., 2003)
and (Mejail, 1999). Under the multiplicative model,
the returned image Z can be thought as two indepen-
dent random variables: the random variable X that
represents the backscatter and the random variable Y
that represent the speckle noise. Different statistical
distributions have been proposed in the literature. In
this work we use the Gamma distribution, Γ, for the
speckle, the reciprocal of Gamma distribution, Γ
−1
,
for the backscatter, which results in the G
0
(Frery
et al., 1996) distribution for the return. These distrib-
utions depend on three parameters: α that is a rough-
ness parameter, γ a scale parameter, and n the equiv-
alent number of looks. In this work, we classify an
image into different regions according to their homo-
geneity degree, which will be refered to section 5. Af-
ter filtering, the image data have undergone changes
in their statistical distribution functions. A study of
the kurtosis and the skewness coefficients obtained af-
ter filtering show that the image data follows a more
gaussian distribution. Then, we classify the image by
using the maximum likelihood method and consider
the normal distribution with different parameters for
each region. The structure of this paper is as follows:
section 2 gives an introduction to stack filters, sec-
33
E. Buemi M., E. Mejail M., C. Jacobo J. and J. Gambini M. (2006).
ADAPTIVE STACK FILTERS IN SPECKLED IMAGERY.
In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 33-40
DOI: 10.5220/0001376400330040
Copyright
c
SciTePress

tion 3 describes the filter design method used in this
work. In section 4 we summarises the G
0
distribution
for SAR images. In section 5 we exhibit the modifi-
cation undergone by data after applying the filter, and
also report on the results of the classification. Finally,
we present the conclusions in section 6.
2 STACK FILTERS: DEFINITIONS
AND DESIGNING
This section is dedicated to a brief synthesis of stack
filter definitions and design. For more details on this
subject, see (Lin and Kim, 1994), (Wendt et al., 1986),
(Astola and Kuosmanen, 1997), (Yoo et al., 1999),
(Coyle and Lin, 1988), (Coyle et al., 1989), (J.Lin
et al., 1990). In the first place the necessary defini-
tions are presented to explain this type of filters.
Definition 1
The threshold operator is given by T
m
:
{0, 1,...,M}→{0, 1}
T
m
(x)=
1 si x ≥ m
0 si x<m
, (1)
X
m
= T
m
(x). (2)
According to this definition, the value of a non-
negative integer number x ∈{0, 1,...,M} can be re-
constructed making the summation of its thresholded
values between 0 and M. The formula corresponding
to this operation is
x =
M
m=1
X
m
. (3)
Figure 1 shows a diagram of the threshold decom-
position of a unidimensional signal. The threshold
operator can be extended to bi-dimensional signals.
Figure 1: Example of threshold decomposition.
Definition 2
Let X=(x
0
,...,x
n−1
) and Y =(y
0
,...,y
n−1
)
be binary vectors of length n, then let us define a re-
lation ≤ given by
X ≤ Y if and only if ∀i, x
i
≤ y
i
. (4)
This relation is reflexive, anti-symmetric and transi-
tive, generating therefore a partial ordering on the set
of binary vectors of fixed length.
Definition 3
A boolean function f : {0, 1}
n
→{0, 1} , where
n is the length of the input vectors, has the stacking
property if and only if
∀X, Y ∈{0, 1}
n
,X≤ Y ⇒ f (X) ≤ f (Y ) . (5)
Definition 4
We say that f is a positive boolean function if and
only if it can be written by means of an expression
that contains only non-complemented input variables.
That is,
f (x
1
,x
2
,...,x
n
)=
K
i=1
j∈P
i
x
j
, (6)
where n is the number of arguments of the function,
K is the number of terms of the expression and the
P
i
are subsets of the interval {1,...,N} .
and
are Boolean operators AND and OR. It is possible
to proof that this type of functions has the stacking
property.
If the function f used to filter an image X fulfills
the stacking property, then from (4) and (5) it is de-
duced that, for two binary images X
i
and X
j
, ob-
tained from X as the result of the application of the
thresholds T
i
and T
j
respectively, the following im-
plication is valid
i ≥ j ⇒ X
i
≤ X
j
⇒ f
X
i
≤ f
X
j
(7)
A stack filter is defined by the function S
f
:
{0,...,M}
n
→{0,...,M}, corresponding to
the Positive Boolean function f (x
1
,x
2
,...,x
n
) ex-
pressed in the given form by (6). The function S
f
can
be expressed by means of
S
f
(X)=
M
m=1
f (T
m
(X)) (8)
In Figure 2 it can be observed a scheme of aplication
of the filter to an unidimensional signal. S
f
represents
the boolean function which filters each binary thresh-
olded signal and whose outputs are added together to
finally obtain the filtered signal.
VISAPP 2006 - IMAGE FORMATION AND PROCESSING
34

Figure 2: Scheme of the stack filter applied to an unidimen-
sional signal. S
f
represents the boolean function applied to
each level.
3 ADAPTIVE ALGORITHMS FOR
STACK FILTERS DESIGN
In this work we applied the stack filter generated with
the fast algorithm described in (Yoo et al., 1999).
This algorithm, arises as a result of studies on the
methods proposed in (Lin and Kim, 1994) and (J.Lin
et al., 1990). To construct a stack filter following
any of these methods, a training process that gen-
erates a positive boolean function that preserves the
stacking property, represented by the so-called deci-
sion vector, is carried out. In what follows, the gen-
eration and behaviour of the decision vector is ex-
plained. An image is defined as the set given by:
{(s, v):s ∈ S ⊆ Z
2
,v ∈ [0,...,M],M ∈ Z},
where s is position and v is the value of a pixel. Let
E and R be two images, where R is the noisy version
of E.AW (s) window is a subimage of R of size
b=r x r centered at position s. Let us define V as a
2
b
dimension vector, and call it the decision vector. In
the training phase of the filter design, for each s ∈ S,
the data in W (s) are decomposed in M thresholds
obtaining M windows w
i
(s), i =1,...,M, where
w
i
(s) is the ith thresholded version of W (s). Then,
for each s ∈ S in the image E ,a threshold e
i
(s) is
defined (notice that here e
i
(s) has dimension 1). If
e
i
(s)=1, then the position on V given by w
i
(s),
considered as a binary number, is increased by one, if
e
i
(s)= 0, then the same position is decremented by 1.
Periodically, V is checked to see wether the stacking
property holds. If not, the decision vector V is suit-
able modified. Finally, the decision vector is trans-
formed into a binary vector that is an implementation
of the positive boolean function f sought. In Figure 3
a filter training example for a 1D signal, is shown .
Let W (s) be a window of length 3 on the noisy sig-
nal, centered at position s, and let E(s) be the value of
the noiseless signal at the same position. In this case,
W (s)=[2, 1, 4], E(s) = [3] and thresholds varying
between 1 and 5 are considered. The decision vector
V is of size 2
3
=8and is represented by the table that
contains at the first column indices expressed in deci-
mal notation, at the second column indices expressed
in binary notation, at the third column the vector val-
ues after n iterations and at the fourth column the vec-
tor values after the n +1iteration.
Figure 3: Scheme of the generation of the stack filter.
The training of this stack filter consists of the al-
ternate application of two different stages: a stage in
which the decision vector is modified according to the
scheme indicated in Figure 3, and a stage in which the
stacking property is checked and enforced on the de-
cision vector.
4 SAR IMAGES. THE
MULTIPLICATIVE MODEL
In this section we introduce the statistical laws com-
monly used under the multiplicative model for Syn-
thetic Aperture Radar (SAR) images. The multiplica-
tive model considers the image returned by the SAR,
named Z, as a product of two independent random
variables, one corresponding to the backscattter X
and the other one corresponding to the speckle noise
Y,so
Z = XY. (9)
Where we suppose independence among the random
variables corresponding to each image pixel. We can
write formula (9) for each pixel (i, j) of an image of
size M × N as:
Z
i,j
= X
i,j
Y
i,j
, 0 ≤ i ≤ M − 1, 0 ≤ j ≤ N − 1.
(10)
The format of the SAR image (complex, amplitude or
intensity) determines the distribution followed by the
speckle noise random variables Y
i,j
. These variables
are i.i.d and the equivalent number of looks n is their
only statistical parameter. On the other hand, the type
of target each pixel belongs to (forest, pasture, crops,
ADAPTIVE STACK FILTERS IN SPECKLED IMAGERY
35

city) determines de most appropiate distribution for
each of the backscatter random variables X
i,j
.
4.1 Speckle Distribution
The speckle noise comes from the coherent addition
of individual returns produced by elements present in
each resolution cell. So, for example, in an image
corresponding to a scene of land covered by vegeta-
tion, the returns from the elements of the plants and
the ground are added taking into account the phase,
yielding as a result a complex number. In an ampli-
tude SAR image, the gray level of each pixel is the
module of the this complex number. In an intensity
SAR image, the gray level of each pixel is the square
of this magnitude.
For every pixel, the model for the speckle noise is
the Γ(n, 2n) distribution, where n is the equivalent
number of looks. Then, within this model the density
function for the speckle noise Y is given by
f
Y
(y)=
n
n
Γ(n)
y
n−1
e
−ny
,y≥ 0. (11)
In SAR images the minimun value for n is 1. This
value corresponds to images generated without mak-
ing the average of several looks. Images generated in
this manner are noiser than those generated with more
number of looks, but they have better azimuth resolu-
tion and, therefore, potencially more information. We
can suppose that the parameter n is known or that it
can be estimated at an initial stage of the image analy-
sis. Therefore, although in theory it would have to be
an integer number, in practice it is necessary to con-
sider it as a real number for the case in which it is
estimated from the data. Figure 4 shows the curves
corresponding to the speckle distribution for different
values of n. The moments of the speckle distribution
Figure 4: Curves of the Γ distribution corresponding to
speckle for number of looks equal to: 1 (solid), 2 (dashes),
3(dots), 4 (dot-dash) and 10 (dot-dot-dash).
are given by:
E[Y
r
]=
1
n
r
Γ(n + r)
Γ(n)
(12)
where r is the moment order and n ≥ 1 is the number
of looks.
4.2 Backscatter Distribution
There are several models for the backscatter, that is,
different statistical distributions exist for the random
variables X
i,j
. From the results presented in (Frery
et al., 1996) it is possible to consider the Generalised
Inverse Gaussian distribution as a general model for
the backscatter. This distribution is very general and
allows us to describe many different targets, but from
an analitical and numerical point of view the estima-
tion of its parameters is very complex and unstable.
This distribution has various particular cases, one of
which: the Inverse Gamma distribution, is of special
interest to this work. This distribution is proposed as
a universal model for SAR data and it leads to the G
0
distribution for the return. The Inverse Gamma dis-
tribution, called Γ
−1
, is characterised by the density
function given by
f
X
(x)=
2
α
γ
α
Γ(−α)
x
α−1
exp
−
γ
2x
, (13)
and its moments are expressed as
E [X
r
]=
γ
2
r
Γ(−α − r)
Γ(−α)
, (14)
where α<0 and |α| >r. In Figure 5 we can see the
curves corresponding to a Γ
−1
density function as we
vary the α parameter keeping the mean value equal to
one.
4.3 Distributions for the Return
The distribution corresponding to the return Z,is
fixed by the distribution of the backscatter X and
the distribution of the speckle Y . Given that Z =
XY and that these random variables are independent,
f
Z
(z) can be calculated as
f
Z
(z)=
R
+
f
Z|Y =y
(z) f
Y
(y) dy, (15)
where f
Z|Y =y
is the density for the return Z con-
sidering X = x constant and f
Y
the density func-
tion of the speckle Y . For the random variable corre-
sponding to the return (intensity format) we have that
Z ∼G
0
(α, γ, n), and the density function is given by
f
Z
(z)=
n
n
Γ(n − α)
γ
2
α
Γ(−α)Γ(n)
z
n−1
γ
2
+ nz
α−n
,
(16)
VISAPP 2006 - IMAGE FORMATION AND PROCESSING
36
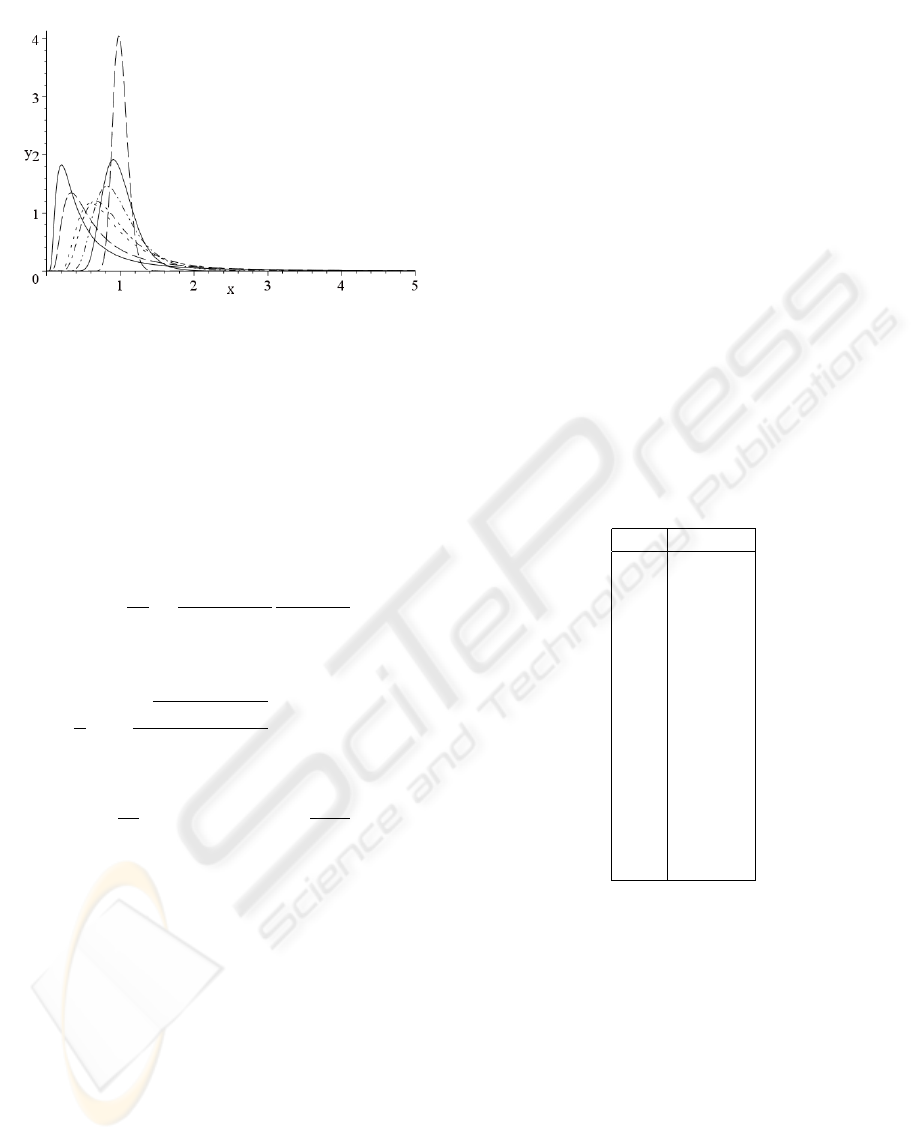
Figure 5: Curves of Γ
−1
distribution with mean value
equal to one and α equal to: −1.5 (solid), −2 (dash), −4
(dots), −5 (dot-dash), −10 (dot-dot-dash), −20 (solid) y
−100(dash).
with α<0, γ>0 and n ≥ 1. Given the indepen-
dence between the backscatter X and the speckle Y ,
the moments of the return Z are the product of the
moments of X and the moments of Y (equations (14)
and ( 12)) yielding
E [Z
r
]=
γ
2n
r
Γ(−α − r)
Γ(−α)
Γ(n + r)
Γ(n)
, (17)
recalling that this moments are finite for −α>r. The
variation coeficient is given by
C
V
=
σ
µ
= −
α (α + n +1)
α
, α<− (n +1),
where
σ
2
=
γ
2
4
α (α + n +1), µ =
−αγ
2
.
This distribution was proposed in (Frery et al., 1996)
as a model for extremely heterogeneous data, but its
utility for description of a great variety of natural and
artificial targets was verified, which resulted in its be-
ing proposed as a universal model for SAR data.
5 RESULTS
This section is dedicated to show the results of apply-
ing a stack filter to synthetic SAR images. These im-
ages are generated in such a way that their data have
different degrees of homogeneity. We consider differ-
ent values of the α parameter and we compute the γ
parameter so that the mean value of the data is unitary.
The α parameter corresponds to image roughness (or
heterogenity). It adopts negative values, varying from
−∞ to 0.Ifα is near 0, then the image data are
extremely heterogeneous (for example: urban areas),
and if α is far of the origin then the data correspond
to a homogeneous region (for example: pasture ar-
eas), the values for forests and crops lay in-between.
The parameter γ is a scale parameter. Finally, in order
to evalute the behaviour of the fiters we carried out
a maximun likelihood classification. The results are
analysed in the classified images, within this images
we compare the filtered and the non-filtered images.
5.1 Statistical Analysis
An important task in statistical analysis is the char-
acterization of the mean value and the variability of
a data set. To this end, the behaviour of some sta-
tistics for filtered and non-filtered images, are com-
pared. Fifteen 100 × 100 images of G
0
distributed
data were generated using the values of α and γ given
in Table 1. In order to design the stack filter, an im-
age formed with the mean values of each region, as
described in section 3, was used.
Table 1: Values of α and γ used in the experiment.
α γ
-1.5 1.00000
-2.0 1.62114
-2.5 2.25000
-3.0 2.88202
-3.5 3.51562
-4.0 4.15012
-4.5 4.78516
-5.0 5.42056
-5.5 6.05621
-6.0 6.69205
-6.5 7.32802
-7.0 7.96409
-7.5 8.60024
-8.0 9.23646
-8.5 9.87273
Examples of these images are shown in Figure 6.
This figure shows the results of applying a 5 × 5 win-
dow size filter to a group of images. Figures 6(a), 6(c)
and 6(e) correspond to the original speckled images
and figures 6(b), 6(d) and 6(f) correspond to the fil-
tered images.
A statistical tool for characterizing the signal to
noise ratio is the variation coefficient, defined as
the quotient between the standard deviation and the
mean value: C
V
=σ/µ. The values of this coefficient
for filtered and non-filtered images are given in Ta-
ble 2. The values corresponding to the filtered images
are lower than the values corresponding to the non-
filtered images, indicating that the effect of filtering
was a decrease in the speckle noise. It can also be
seen that the value of the variation coefficient C
V
is
ADAPTIVE STACK FILTERS IN SPECKLED IMAGERY
37

(a) α=−1.5 (b) Filtered image
(c) α=−4.0 (d) Filtered image
(e) α=−8.5 (f) Filtered image
Figure 6: Synthetic images (left) and their corresponding
filtered images (right).
lower when the α parameter is lower for both, filtered
and non-filtered images. In order to assess the nor-
mality of the data, the skewness and kurtosis statistics
were used. They are defined by
SK =
N
i=1
(Y
i
−
¯
Y )
3
(N−1)s
3
K =
N
i=1
(Y
i
−
¯
Y )
4
(N−1)s
4
where, Y
1
,Y
2
,...,Y
N
are univariate data,
¯
Y is the
mean value, s is the standard deviation, and N is the
sample size. For a normal distribution, the skewness
SK is zero (symmetric density) and the kurtosis K is
3.
The distribution of the data is modified when they
are filtered. If we consider the skewness and the kur-
tosis as a measure of asymmetry and peakedness be-
tween the data and the density, we can state that the
data are more Gaussian after filtering. This can be
seen in Tables 3 and 4 where the skewness and the
kurtosis for each α value are shown.
Table 2: Variation coefficients.
α C
V
non-filtered C
V
filtered
images images
-1.5 1.020400 0.327207
-2.0 0.803039 0.251616
-2.5 0.738860 0.256685
-3.0 0.685162 0.240635
-3.5 0.668856 0.239666
-4.0 0.637395 0.230422
-4.5 0.612268 0.223510
-5.0 0.613924 0.227741
-5.5 0.598406 0.224422
-6.0 0.591566 0.221399
-6.5 0.588123 0.217759
-7.0 0.571000 0.215808
-7.5 0.585607 0.216695
-8.0 0.577546 0.221254
-8.5 0.577740 0.216642
It can be noticed that, the more heterogeneous the
non-filtered data are, that is α closer to 0, the higher
the values for the skewness and kurtosis.
Table 3: Skewness.
α Skewness non-filtered Skewness filtered
images images
-1.5 5.79204 0.542360
-2.0 2.71243 0.452572
-2.5 2.17279 0.354620
-3.0 2.06542 0.404203
-3.5 1.79158 0.396256
-4.0 1.56213 0.287269
-4.5 1.30829 0.283221
-5.0 1.18022 0.339163
-5.5 1.15137 0.323194
-6.0 1.15225 0.261475
-6.5 1.03733 0.322413
-7.0 0.972302 0.381224
-7.5 0.990236 0.317580
-8.0 0.964581 0.381402
-8.5 0.904661 0.286144
5.2 Maximum Likelihood
Classification
Finally, ten 128 × 128 images were generated with
two regions with α = −1.5, γ =1for the left side,
α = −10, γ =1for the right side and n =1for
both sides. The influence of stack filtering on maxi-
mum likelihood classification performance was stud-
ied. Figure 7 shows an example of a classified image
with and without filtering.
VISAPP 2006 - IMAGE FORMATION AND PROCESSING
38

Table 4: Kurtosis.
α Kurtosis non-filtered Kurtosis filtered
images images
-1.5 81.5878 1.05008
-2.0 14.7974 0.797948
-2.5 9.90102 0.330502
-3.0 10.2707 0.229317
-3.5 7.36229 0.852436
-4.0 5.14167 0.117459
-4.5 3.10693 0.318509
-5.0 2.43030 0.145160
-5.5 2.35810 0.123555
-6.0 2.79451 0.297602
-6.5 1.93492 0.233789
-7.0 1.39388 0.328363
-7.5 1.66122 0.238216
-8.0 1.36633 0.299916
-8.5 0.998106 0.0621805
Table 5 shows the corresponding confusion matrix:
odd lines correspond to non-filtered images and even
lines correspond to filtered images. Data must be read
as follows: R
i
/R
j
means the percentage of pixels that
belong to region R
j
but were classified into region R
i
.
I
k
and F
k
correspond to the non-filtered image and
to the filtered imge, respectively. From these values
it can be seen that the classification performance was
better for filtered images than for non- filtered images.
(a) Original image (b) Image 7(a) classified
(c) Filtered image (d) Image 7(c) classified
Figure 7: Synthetic, filtered and classified images.
Table 5: Confusion matrix.
Imagen R
1
/R
1
R
2
/R
1
R
2
/R
2
R
1
/R
2
I
0
71.46 28.54 89.27 10.73
F
0
93.57 6.43 94.60 5.41
I
1
70.69 29.31 89.55 10.45
F
1
93.35 6.65 94.60 5.39
I
2
72.51 27.49 89.59 10.41
F
2
93.48 6.52 94.57 5.43
I
3
71.94 28.05 89.66 10.34
F
3
92.43 7.57 94.60 5.41
I
4
71.58 28.42 89.05 10.95
F
4
92.21 7.79 94.58 5.42
I
5
71.67 28.33 89.72 10.28
F
5
93.10 6.90 94.48 5.52
I
6
71.09 28.91 89.46 10.53
F
6
93.35 6.65 94.59 5.41
I
7
70.76 29.24 88.49 11.51
F
7
92.87 7.13 94.57 5.43
I
8
71.53 28.47 89.53 10.47
F
8
91.99 8.01 94.59 5.41
I
9
71.81 28.19 89.37 10.63
F
9
91.76 8.24 94.52 5.48
6 CONCLUSION
In this work, a study on the behaviour of adaptive
stack filters, applied to synthetic aperture radar (SAR)
images, was performed. The fundamentals of stack
filters were presented. These filters were applied to
simulated SAR images generated using the G
0
law
and were based on the algorithm proposed by (Yoo
et al., 1999). The statistical distribution of the fil-
tered data was studied, and it was observed that they
no longer followed the above mentioned distribution.
We could infer that it turned out to be more similar
to the Gaussian distribution. Filtered and non-filtered
images were classified according to the maximum
likelihood criterion. The classification performance
was better for filtered images than for non-filtered im-
ages.
REFERENCES
Astola, J. and Kuosmanen, P. (1997). Fundamentals of Non-
linear Digital Filtering. CRC Press, Boca Raton.
Coyle, E. J., Lin, J.-H., and Gabbouj, M. (1989). Opti-
mal stack filtering and the estimation and structural
approaches to image processing. IEEE Trans. Acoust.,
Speech, Signal Processing, 37:2037–2066.
Coyle, J. and Lin, J.-H. (1988). Stack filters and the mean
absolute error criterion. IEEE Trans. Acoust., Speech,
Signal Processing, 36:1244–1254.
ADAPTIVE STACK FILTERS IN SPECKLED IMAGERY
39

Frery, A. C., Correia, A. H., Renn
´
o, C. D., Freitas, C. C.,
Jacobo-Berlles, J., Mejail, M. E., and Vasconcellos,
K. L. P. (1999). Models for synthetic aperture radar
image analysis. Resenhas (IME-USP), 4(1):45–77.
Frery, A. C., M
¨
uller, H.-J., Yanasse, C. C. F., and
Sant’Anna, S. J. S. (1996). A model for extremely het-
erogeneous clutter. IEEE Transactions on Geoscience
and Remote Sensing, 35(3):648–659.
Goodman, J. W. (1976). Some fundamental properties of
speckle. Journal of the Optical Society of America,
66:1145–1150.
J.Lin, H., M.Sellke, T., and J.Coyle, E. (1990). Adaptive
stack filtering under the mean absolute error criterion.
IEEE Trans. Acoust., Speech, Signal Process, 38:938–
954.
Lin, J.-H. and Kim, Y. (1994). Fast algorithms for train-
ing stack filters. IEEE Trans. Signal Processing,
42(3):772–781.
Mejail, M. E. (1999). La Distribucin G
0
A
en el modelado
y Anlisis de Imgenes SAR. PhD thesis, Departamento
de Computacin, Facultad de Ciencias Exactas y Natu-
rales,Universidad de Buenos Aires.
Mejail, M. E., Frery, A. C., Jacobo-Berlles, J., and Bus-
tos, O. H. (2001). Approximation of distributions for
SAR images: proposal, evaluation and practical con-
sequences. Latin American Applied Research, 31:83–
92.
Mejail, M. E., Jacobo-Berlles, J., Frery, A. C., and Bustos,
O. H. (2003). Classification of SAR images using a
general and tractable multiplicative model. Interna-
tional Journal of Remote Sensing, 24(18):3565–3582.
Oliver, C. and Quegan, S. (1998). Understanding synthetic
aperture radar images. Artech House.
Wendt, P., Coyle, E. J., and N.C. Gallangher, J. (1986).
Stack filters. IEEE Trans. Acoust. Speech Signal
Processing, 34:898–911.
Yoo, J., Fong, K. L., Huang, J.-J., Coyle, E. J., and III, G.
B. A. (1999). A fast algorithm for designing stack
filters. IEEE Trans.on image processing, 8(8):772–
781.
VISAPP 2006 - IMAGE FORMATION AND PROCESSING
40
