IMAGE MATCHING BY RANSAC USING MULTIPLE
NON-UNIFORM DISTRIBUTIONS COMPUTED FROM IMAGES
Yasushi Kanazawa and Yoshihiro Ito
Department of Knowledge-based Information Engineering, Toyohashi University of Technology
1–1 Hibarigaoka, Tempaku, Toyohashi, Aichi 441-8580 JAPAN
Keywords:
image matching, RANSAC, multiple homographies, planar region detection, uncalibrated stereo.
Abstract:
We propose an accurate method for establishing point correspondences between two images taken by an un-
calibrated stereo. We explores the case of a scene with multiple planes and we detect the homographies of the
planes by using a RANSAC-like algorithm. For random sampling in RANSAC, we define three nonuniform
sampling weights that are computed from feature points in the images. By introducing these weights, our
method can detect more accurate matches than the usual methods. Furthermore, our method can establish the
correspondence stably irrespective of the scene is faraway or not. We demonstrate effectiveness of our method
by real image examples.
1 INTRODUCTION
Establishing point correspondences over multiple im-
ages is the first step of many computer vision appli-
cations. Therefore, various matching methods have
been proposed (Kanazawa and Kanatani, 2004b; Ma-
ciel and Costeira, 2002; Olson, 2002; Zhang et al.,
1995)
RANSAC (Fischler and Bolles, 1981) and LMedS
(Rousseeuw and Leroy, 1987) are very powerful
methods for estimating parameters over images. They
are also very robust to outliers in data. So, for estab-
lishing point correspondences, many methods based
on them have been proposed (Torr and Davidson,
2003; Torr and Zisserman, 1998; Torr and Zisserman,
2000). In those procedures, we usually use a uniform
distribution for sampling data. It is reasonable when
we want to estimate global parameters over images.
For example, for estimating the homography to make
the panoramic image from two images, RANSAC and
LMedS work very well. For estimating the funda-
mental matrix of an image pair, they also work fine.
Because these matrices are the global parameters be-
tween the two images.
When there are multiple planes in a scene, we can
compute the fundamental matrix from the homogra-
phies of the planes (Hartley and Zisserman, 2000).
Such the fundamental matrix is more accurate than
that computed from point matches and can be de-
composed into camera parameters stably (Kanazawa
et al., 2004). However, if we want to estimate the ho-
mographies for small planes in the scene, RANSAC
and LMedS with a uniform distribution do not work
well. Because the probability of the four matches,
which are chosen by a uniform distribution, being on
the same plane is very small. Then, we need many
iterations for estimating such the homographies. In
addition, we often obtain the homographies for non-
existing planes. For such the case, we need some
knowledge about the existing planes (Dick et al.,
2000), a criterion for judgment whether the region
is planar or not (Kanazawa et al., 2004), or detect-
ing special features for planar regions (Matas et al.,
2002).
In this paper, we propose an accurate method for
establishing point correspondences based on detect-
ing the homographies of multiple planes in a scene
using a RANSAC-like algorithm. Instead of using a
uniform distribution for random sampling, we intro-
duce three nonuniform sampling weights: concentrate
likelihoods, coplanarity likelihoods, and correspond-
ing likelihoods. These likelihood distributions are de-
fined from the locations of feature points and residu-
als of template matching. By introducing these likeli-
hoods, our method can detect more accurate matches
than other methods. Furthermore, our method can es-
tablish the correspondence stably irrespective of the
scene is faraway or not. We demonstrate effectiveness
of our method by real image examples.
377
Kanazawa Y. and Ito Y. (2006).
IMAGE MATCHING BY RANSAC USING MULTIPLE NON-UNIFORM DISTRIBUTIONS COMPUTED FROM IMAGES.
In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 377-382
DOI: 10.5220/0001372103770382
Copyright
c
 SciTePress

t
X
Y
Z
Y
Z
P
x
Rx
O
O
X
’
’
’
’
’
Figure 1: The camera model and the co-
ordinates systems.
Image Plane
Optical Center
3D surface
Figure 2: Coplanarity likelihood.
β
1.0
ρ
y = a x
α
index
q(Pβ|Pα)
Figure 3: Planar point likelihood.
2 COMPATIBILITY OF
FUNDAMENTAL MATRIX AND
HOMOGRAPHIES
We assume that the camera model is the pinhole
model. We take the first camera as a reference coordi-
nate system and place the second camera in a position
obtained by translating the first camera by vector t
and rotating it around the center of the lens by matrix
R. The two cameras may have different focal lengths
f and f

.
Let (x, y) be the image coordinates of a feature
point P projected onto the image plane of the first
camera, and (x

,y

) be those for the second camera.
We use the following three-dimensional vectors to
represent them (the superscript  denotes transpose):
x =(x/f
0
,y/f
0
, 1)

, x

=(x

/f
0
,y

/f
0
, 1)

.
(1)
Here, f
0
is a scale factor for stabilizing computation.
We consider the vectors x
i
and x

i
for feature points
P
i
, i =1, ..., N. As shown in Fig. 1, the vectors x
i
and x

i
must satisfy the following epipolar equation
(Hartley and Zisserman, 2000; Kanatani, 1996):
(x
i
, Fx

i
)=0. (2)
Here, (a, b) denotes the inner product of vectors a
and b. The matrix F , which is called the fundamental
matrix, is a singular matrix of rank 2.
When all the point P
i
lie on a plane Π, the vectors
x
i
and x

i
are related in the following form (Hartley
and Zisserman, 2000; Kanatani, 1996):
x

i
= Z[Hx
i
]. (3)
Here, Z[ · ] designates a scale normalization to make
the third component 1. The matrix H, which is called
the homography, is a nonsingular matrix.
When the feature points P
j
, j =1, ..., M lied on a
plane in a scene, Eqs. (2) and (3) are satisfied simulta-
neously. This time, the homography H is compatible
to the fundamental matrix F (Hartley and Zisserman,
2000) and the matrix product FH must be a skew-
symmetric matrix:
FH + H

F

= O. (4)
Using the compatibility (4), we can compute the
fundamental matrix F from two or more homogra-
phies H
1
, ..., H
K
, K ≥ 2. In addition, if we
compute the homographies by an optimal method
(Kanatani et al., 2000) and compute the fundamental
matrix from the homographies, the obtained funda-
mental matrix is more accurate than that directly com-
puted from point matches (Kanazawa et al., 2004).
3 WEIGHTS FOR RANDOM
SAMPLING
For detecting multiple planes from two images taken
by an uncalibrated stereo, we must estimate homo-
graphies for the planes from point matches between
the two images. Generally, we can robustly esti-
mate a global homography between two images by
RANSAC (Fischler and Bolles, 1981) and LMedS
(Rousseeuw and Leroy, 1987). But, if we want to es-
timate the homographies of local or small planes in
the scene, RANSAC and LMedS do not work well.
Because the probability of chosen four matches being
on the same plane is very small due to using a uni-
form distribution for random sampling. Therefore, we
need many iterations, but we may often obtain the ho-
mographies for non-existing planes. However, if we
know some knowledge about the planes in the scene
and we defined the sampling weights for random sam-
pling using the knowledge, we can efficiently choose
pairs on the same plane and can estimate the homog-
raphy for them. So, we define three weights for doing
random sampling. We compute them from the loca-
tions of feature points and the residuals of template
matching.
3.1 Coplanarity Likelihoods
First, we define coplanarity likelihood between two
feature points in an image. The same likelihoods
have been proposed by the Kanazawa and Kawakami
(Kanazawa and Kawakami, 2004), however, we add
physical interpretation to them in this paper.
Considering two points that are on a 3-D surface
(Fig. 2), we can regard the proximity two points are
VISAPP 2006 - MOTION, TRACKING AND STEREO VISION
378

on the same plane whether the surface is exactly pla-
nar or not. On the other hand, when the distance be-
tween the two points is long, we regard the two points
are not on the same plane if the surface is not planar.
So, the proximity two points on the image have high
likelihood that they are on the same plane. Then, we
define a likelihood of coplanarity with respect to the
two points by the distance between them.
Let I
1
and I
2
be the sets of all the feature points
in I
1
and I
2
, respectively. For P
α
, P
β
∈I
1
, let d
αβ
be the Euclidean distance between them. We define
the conditional likelihood p(P
β
|P
α
) by the following
equations.
p(P
β
|P
α
)=

1
Z
α
e
−s
α
d
2
αβ
··· α = β
0 ··· α = β
, (5)
where, Z
α
=

N
β=α
e
−s
α
d
2
αβ
and N is the number of
the feature points on the image I
1
. We call this like-
lihoods the coplanarity likelihoods, which indicates
a likelihood about that P
α
and P
β
are on the same
plane. Here, the parameter s
α
is determined by solv-
ing the following equations.
N

β=1
(d
αβ
−
¯
d
α
)e
−s
α
d
2
αβ
=0,
¯
d
α
=
1
N
N

β=1
d
αβ
.
(6)
3.2 Planar Point Likelihood
Next, we define a planar point likelihood of the
feature point P
α
using the coplanarity likelihood
p(P
β
|P
α
).
For each P
α
, we define the following conditional
cumulative likelihood
q(P
β
|P
α
)=
β

µ=1
p(P
µ
|P
α
), (7)
where, the p(P
µ
|P
α
) are sorted in descending order
with respect to P
µ
for each P
α
.
In the space of the cumulative likelihood q(P
β
|P
α
),
we consider a line y = a
α
x passing through the origin
and the point that q(P
β
|P
α
) = ρ (Fig.3). Using the
coefficient a
α
of the line, we define the planar point
likelihood ˆp(P
α
) for the point P
α
by
ˆp(P
α
)=
a
α

α∈I
1
a
α
. (8)
3.3 Corresponding Likelihood
Finally, we define corresponding likelihoods by the
residuals of template matching.
Correlations or residuals obtained by template
matching are often used for establishing point corre-
spondences between two images. We must not ab-
solutely trust them, because it depends on the posi-
tions and the orientations of the two cameras. How-
ever, the correct pairs usually have high correlation
values. So, we define the likelihood of correspon-
dence for each match by the residual of template
matching.
Let P
β
be a feature point in I
1
and Q
β

be a feature
point in another image I
2
. Let j
ββ

be the residual
of template matching between them. Using j
ββ

,we
define the conditional likelihoods p

(Q
β

|P
β
) as fol-
lows:
p

(Q
β

|P
β
)=
1
Z
β
e
−t
β
j
2
ββ

,Z
β
=
M

β

=1
e
−t
β
j
2
ββ

(9)
Here, M is the number of the feature points in the im-
age I
2
. We call this likelihoods the correspondence
likelihoods, which indicate that the pair {P
β
, Q
β

}
is the correct match. Here, the parameter t
β
is deter-
mined by the same way as the coplanarity likelihoods:
M

β

=1
(j
ββ

−
¯
j
β
)e
−t
β
j
2
ββ

=0,
¯
j
β
=
1
L
L

β

=1
j
ββ

(10)
Here, the residuals j
ββ

are sorted in ascending order
for each β and L is the average index number of the
correct matches (1 ≤ L ≤ M ).
3.4 RANSAC with the Three
Nonuniform Likelihoods
Using these likelihood as the weights for random sam-
pling, we can efficiently choose candidate matches
that are coplanar in the scene and have high corre-
lation values. We also can avoid combinational ex-
plosion for choosing the candidate matches.
Here, in advance, we sort the likelihoods in de-
scending order and compute cumulative likelihoods,
respectively. In each random sampling, we first gen-
erate one random number x in the range [0, 1) using a
uniform distribution, then increase β from 1 and find
β that satisfies
q
β−1
≤ x<q
β
, (11)
where q
β
is a cumulative likelihood and q
0
=0.
The procedure of our method is as follows:
1. Randomly choose a point P
α
in I
1
using the planar
point likelihood ˆp(P
α
).
2. Choose 4 points P
β
1
, P
β
2
, P
β
3
, and P
β
4
in I
1
using
the coplanarity likelihood p(P
β
|P
α
) with respect to
P
α
.
IMAGE MATCHING BY RANSAC USING MULTIPLE NON-UNIFORM DISTRIBUTIONS COMPUTED FROM
IMAGES
379

(a) (b) (c)
(d) (e) (f) (g)
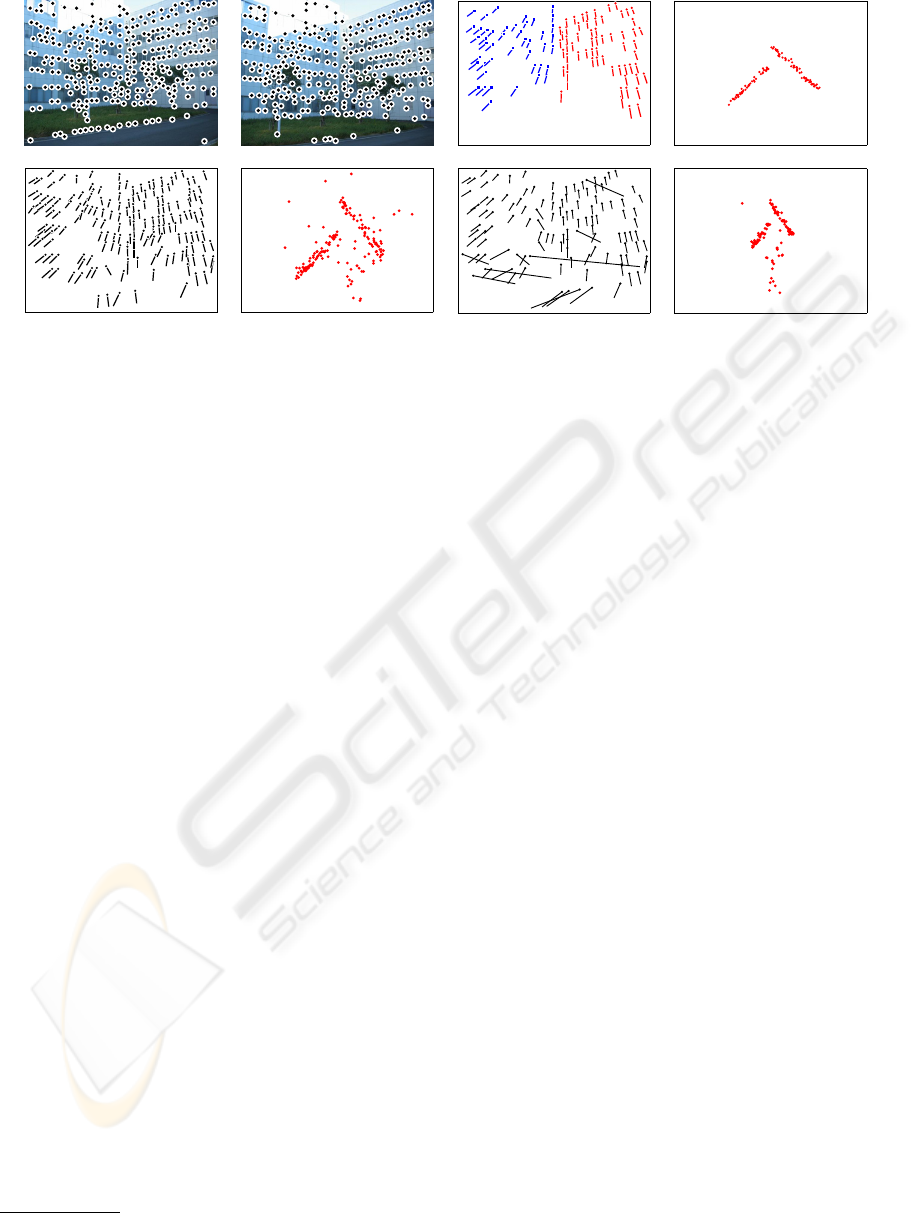
Figure 4: (a) A stereo image pair and detected feature points. (b) Correspondences and planar regions and obtained by the
proposed method. (c) 3-D shape (top view) from (b). (d) Correspondences obtained by the method of Kanazawa and Kanatani
(Kanazawa and Kanatani, 2004b). (e) 3-D shape (top view) from (d). (f) Correspondences obtained by the standard RANSAC.
(g) 3-D shape (top view) from (f).
3. Choose 4 matches {P
β
1
,Q
β

1
}, {P
β
2
,Q
β

2
},
{P
β
3
,Q
β

3
}, and {P
β
4
,Q
β

4
} using the corre-
sponding likelihoods p

(Q
β

|P
β
1
), p

(Q
β

|P
β
2
),
p

(Q
β

|P
β
3
), p

(Q
β

|P
β
4
), respectively. Here,
Q
β

1
, Q
β

2
, Q
β

3
, Q
β

4
∈I
2
.
4. Check the chosen 4 matches are skewed or not
(Kanazawa and Kawakami, 2004). If the matches
are skewed, back to the step 1.
5. Compute a homography H
α
from chosen 4
matches.
6. Let S
α
be the set of the matches {P
γ
,Q

γ
} which
satisfy
E(P
γ
,Q

γ
, H
α
) <d and p

(Q

γ
|P
γ
) <t.
where P
γ
∈I
1
and Q

γ
∈I
2
. Here, t and d
are the thresholds specified by users. The func-
tion E(P
γ
,Q

γ
, H ) is an error function (or resid-
ual) of the match {P
γ
,Q

γ
} and the homography
H
α
, which is obtained by Eq. (3). Then, let M
α
be the number of the elements of S
α
.
7. Repeat the above computation until M
α
reaches its
maximum.
8. Finally, enforce uniqueness with respect to
E(P
γ
,Q

γ
, H
α
) to the resulting S
α
and re-
compute the homography H
α
from them.
By repeating the above procedure, we can obtain one
or more homographies of the planes in the scene.
We summarize the above procedure as follows. In
the first image, by using the planar point likelihood,
we first choose a “seed” in the region that includes
many feature points. Such region can be regarded as
planar in the scene. We then choose 4 points that
are close to the seed by using the coplanarity likeli-
hood about the seed. We finally choose correspond-
ing points in the second image for the 4 points chosen
from the first image by using the correspondence like-
lihoods. After computing a homography from the 4
matches, we then make the consensus set for the com-
puted homography from the set of the matches that
have high correspondence probabilities and satisfy the
specified degree to the computed homography. By re-
peating this procedure, we can find the consensus set
that have the maximum number of the elements. So,
we can regard all the correspondences in the obtained
consensus set are in the same planar region. Finally,
we compute the homography from them by an op-
timal method (Kanatani et al., 2000). If we obtain
multiple homographies in the scene, we compute the
fundamental matrix from the obtained homographies
using the compatibility (4). Furthermore, if we need
the correspondences which original 3-D points are not
on any planes, we can check each candidate matches
using the epipolar equation (2) using the computed
fundamental matrix.
4 EXPERIMENTAL RESULTS
We show some experiments using real images.
Fig. 4 shows a real image example of a scene of
brick walls. Fig. 4 (a) shows a stereo image pair
and the feature points detected by Harris operator
(Harris and Stephens, 1988). Fig. 4 (b) shows the
correspondences and the planar regions obtained by
our method. Here, we show only the correspon-
dences on the detected planar regions. Fig. 4 (d)
shows the correspondences obtained by the method of
Kanazawa and Kanatani
1
(Kanazawa and Kanatani,
1
We used the program code placed at
http://www.img.tutkie.tut.ac.jp/programs/index-e.html
VISAPP 2006 - MOTION, TRACKING AND STEREO VISION
380

(a) (b) (c)
(d) (e) (f) (g)
Figure 5: (a) A stereo image pair and detected feature points. (b) Result by the proposed method. (c) 3-D shape (top view)
from (b). (d) Result by the method of Kanazawa and Kanatani (Kanazawa and Kanatani, 2004b). (e) 3-D shape (top view)
from (d). (f) Result the standard RANSAC. (g) 3-D shape (top view) from (f).
2004b). Fig. 4 (f) shows the result obtained by the
standard RANSAC only using the epipolar constraint.
In these results, we show the correspondences using
line segments whose endpoints are the positions of a
pair of points. We can see that the proposed method
can establish many correct matches compared with
the other methods.
Fig. 4 (c), (e), and (g) show the reconstructed 3-
D shapes from the correspondences (b), (d), and (f),
respectively. Here, we use the method of Kanatani
and Matsunaga (Kanatani and Matsunaga, 2000) for
decomposing the fundamental matrix into the camera
parameters. In these 3-D reconstructions, the angles
of the walls are about 90 degrees in Fig. 4 (c), 95 de-
grees in Fig. 4 (e), and 100 degrees in Fig. 4 (g). We
see the fundamental matrix obtained by our method is
accurate compared with the other methods.
Fig. 5 shows an example in a scene of buildings.
We see that there are many wrong matches in the re-
sults obtained by the other methods. But, we see that
there are few wrong matches in the result obtained by
our method. The angles of the walls in 3-D shapes
are about 94 degrees in Fig. 5 (c), 80 degrees in Fig. 5
(e), and 69 degrees in Fig. 5 (g). Again, we see the
3-D shape obtained by the proposed method is more
accurate than the other methods.
Fig. 6 shows an example for a faraway scene. Gen-
erally in a faraway scene, we can detect only one
plane, but we cannot compute the fundamental ma-
trix because the scene is degeneracy. So, we can-
not obtain the correspondences using the standard
RANSAC. We compare the results by our method
and the method for image mosaicing proposed by
Kanazawa and Kanatani
2
(Kanazawa and Kanatani,
2
We used the program code placed at
http://www.img.tutkie.tut.ac.jp/programs/index-e.html
2004a). Fig. 6 (b) and (c) show the correspondences
obtained by our method and the method of Kanazawa
and Kanatani. Fig. 6 (d) and (e) show panoramic
(difference) images from (b) and (c). We see our
method detect many correct matches and the gener-
ated panoramic image is also accurate.
In our method, we need not the judgment whether
the scene is degenerated or not (Kanazawa and
Kanatani, 2004b). In other words, our method can es-
tablish the correspondence stably irrespective of the
scene is faraway or not.
For these examples, we stopped the search when
no update occurred 20000 times consecutively in the
iteration in our method. The total computation times
were 335 seconds for Fig. 4, 341 seconds for Fig. 5,
and 58 seconds for Fig. 6. We used Pentium 4, 2.4
GHz for the CPU with 512 MB main memory and
Linux for the OS.
5 CONCLUSION
We have proposed an accurate method for establish-
ing point correspondences based on detecting one or
more planes by random sampling. Instead of using
a uniform distribution in random sampling, we intro-
duce three nonuniform likelihoods, which are defined
by the feature points and their correlations. By us-
ing these likelihoods, our method can choose correct
matches efficiently in random sampling. So we can
detect more correct matches than the other methods.
Furthermore, our method can establish the correspon-
dence stably irrespective of the scene is faraway or
not. By real image examples, we have demonstrated
that the proposed method is robust and accurate.
In future works, we must reduce processing times
of the method.
IMAGE MATCHING BY RANSAC USING MULTIPLE NON-UNIFORM DISTRIBUTIONS COMPUTED FROM
IMAGES
381

(a) (b) (c)
(d) (e)
Figure 6: (a) A stereo image pair and detected feature points. (b) Result by the proposed method. (c) Result by the method of
Kanazawa and Kanatani (Kanazawa and Kanatani, 2004a). (d) Panoramic image from (b). (e) Panoramic image from (c).
ACKNOWLEDGEMENTS
This work was supported in part by the Ministry of
Education, Culture, Sports, Science and Technology,
Japan, under the Grant for 21st Century COE Program
“Intelligent Human Sensing.”
REFERENCES
Dick, A., Torr, P., and Cipolla, R. (2000). Automatic 3d
modeling of architecture. In Proc. 11th British Ma-
chine Vision Conf., pages 372–381, Bristol, U.K.
Fischler, M. and Bolles, R. (1981). Random sample consen-
sus: A paradigm for model fitting with applications to
image analysis and automated cartography. Comm.
ACM, 24(6):381–395.
Harris, C. and Stephens, M. (1988). A combined corner and
edge detector. In Proc. 4th Alvey Vision Conf., pages
147–151, Manchester, U.K.
Hartley, R. and Zisserman, A. (2000). Multiple View Geom-
etry. Cambridge University press, Cambridge.
Kanatani, K. (1996). Statistical Optimization for Geometric
Computation: Theory and Practice. Elsevier Science,
Amsterdam.
Kanatani, K. and Matsunaga, C. (2000). Closed-form ex -
pression for focal lengths from the fundamental ma-
trix. In Proc. 4th Asian Conf. Comput. Vision, pages
128–133, Taipei, Taiwan.
Kanatani, K., Ohta, N., and Kanazawa, Y. (2000). Optimal
homography computation with a reliability measure.
IEICE trans. Inf. & Syst., E83-D(7):1369–1374.
Kanazawa, Y. and Kanatani, K. (2004a). Image mosaic-
ing by stratified matching. Image Vision Comput,
22(2):93–103.
Kanazawa, Y. and Kanatani, K. (2004b). Robust image
matching preserving global consistency. In Proc. 6th
Asian Conf. Comput. Vision, pages 1128–1133, Jeju
Island, Korea.
Kanazawa, Y. and Kawakami, H. (2004). Detection of pla-
nar regions with uncalibrated stereo using distribu-
tions of feature points. In Proc. 15th British Machine
Vision Conf., pages 247–256, London, U.K.
Kanazawa, Y., Sakamoto, T., and Kawakami, H. (2004).
Robust 3-d reconstruction using one or more homo-
graphies with uncalibrated stereo. In Proc. 6th Asian
Conf. Comput. Vision, pages 503–508, Jeju Island,
Korea.
Maciel, J. and Costeira, J. (2002). Robust point correspon-
dence by concave minimization. Image Vision Com-
put., 20(9/10):683–690.
Matas, J., Chum, O., Urban, M., and Pajdla, T. (2002). Ro-
bust wide baseline stereo from maximally stable ex-
tremal regions. In Proc. 13th British Machine Vision
Conf., pages 384–393, Cardiff, U.K.
Olson, C. F. (2002). Maximum-likelihood image matching.
IEEE Trans. Patt. Anal. Mach. Intell., 24(6):853–857.
Rousseeuw, P. J. and Leroy, A. (1987). Robust Regression
and Outlier Detection. Wiley, New York.
Torr, P. and Davidson, C. (2003). Impsac: Synthesis of
importance sampling and random sample consensus.
IEEE Trans. Patt. Anal. Mach. Intel., 25(3):354–364.
Torr, P. and Zisserman, A. (1998). Robust computation and
parameterization of multiple view geometry. In Proc.
6th Int. Conf. Computer Vision, pages 727–732, Bom-
bay, India.
Torr, P. and Zisserman, A. (2000). Mlesac: A new robust
estimator with application to estimating image geom-
etry. Comput. Vis. Image. Understand., 78:138–156.
Zhang, Z., Deriche, R., Faugeras, O., and Luong, Q.-T.
(1995). A robust technique for matching two uncal-
ibrated images through the recovery of the unknown
epipolar geometry. Artif. Intell., 78:87–119.
VISAPP 2006 - MOTION, TRACKING AND STEREO VISION
382