
IMPROVED RECONSTRUCTION OF IMAGES
DISTORTED BY WATER WAVES
Arturo Donate and Eraldo Ribeiro
Department of Computer Sciences
Florida Institute of Technology
Melbourne, FL 32901
Keywords:
Image recovery, reconstruction, distortion, refraction, motion blur, water waves, frequency domain.
Abstract:
This paper describes a new method for removing geometric distortion in images of submerged objects observed
from outside shallow water. We focus on the problem of analyzing video sequences when the water surface
is disturbed by waves. The water waves will affect the appearance of the individual video frames such that
no single frame is completely free of geometric distortion. This suggests that, in principle, it is possible to
perform a selection of a set of low distortion sub-regions from each video frame and combine them to form
a single undistorted image of the observed object. The novel contribution in this paper is to u se a multi-
stage clustering algorithm combined with frequency domain measurements that allow us to select the best
set of undistorted sub-regions of each frame in the video sequence. We evaluate the new algorithm on video
sequences created both in our laboratory, as well as in natural environments. Results show that our algorithm
is effective in removing distortion caused by water motion.
1 INTRODUCTION
In this paper, we focus on the problem of recovering
a single undistorted image from a set of non-linearly
distorted images. More specifically, we are interested
in the case where an object submerged in water is
observed by a video camera from a static viewpoint
above the water. The water surface is assumed to
be disturbed by waves. Figure 1 shows a sample of
frames from a video of a submerged object viewed
from above. This is an interesting and difficult prob-
lem mainly when the geometry of the scene is un-
known. The overall level of distortion in each frame
depends on three main parameters of the wave model:
the amplitude, the speed of oscillation, and the slope
of the local normal vector on the water surface. The
amplitude and slope of the surface normal affect the
refraction of the viewing rays causing geometric dis-
tortions while the speed of oscillation causes motion
blur due to limited video frame rate.
Our goal in this paper is to recover an undistorted
image of the underwater object given only a video of
the object as input. Additionally, no previous knowl-
edge of the waves or the underwater object is as-
sumed. We propose to model the geometric distor-
tions and the motion blur separately from each other.
Figure 1: An arbitrary selection of frames from our low
energy wave data set.
We analyse geometric distortions via clustering, while
measuring the amount of motion blur by analysis in
the frequency domain in an attempt to separate high
and low distortion regions. Once these regions are
acquired, we combine single samples of neighboring
low distortion regions to form a single image that best
represents the object.
We test our method on different data sets created
both in the laboratory as well as outdoors. Each
experiment has waves of different amplitudes and
speeds, in order to better illustrate its robustness. Our
current experiments show very promising results.
The remainder of the paper is organized as follows.
We present a review of the literature in Section 2. In
228
Donate A. and Ribeiro E. (2006).
IMPROVED RECONSTRUCTION OF IMAGES DISTORTED BY WATER WAVES.
In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 228-235
DOI: 10.5220/0001369202280235
Copyright
c
SciTePress

Section 3, we describe the geometry of refraction dis-
tortion due to surface waves. Section 4 describes the
details of our method. In Section 5, we demonstrate
our algorithm on video sequences acquired in the lab-
oratory and outdoors. Finally, in Section 6, we present
our conclusions and directions for future work.
2 RELATED WORK
Several authors have attempted to approach the gen-
eral problem of analyzing images distorted by wa-
ter waves. The dynamic nature of the problem re-
quires the use of video sequences of the target scene
as a primary source of information. In the discussion
and analysis that follow in this paper, we assume that
frames from an acquired video are available.
The literature has contributions by researchers in
various fields including computer graphics, computer
vision, and ocean engineering. Computer graphics
researchers have primarily focused on the problem
of rendering and reconstructing the surface of the
water (Gamito and Musgrave, 2002; Premoze and
Ashikhmin, 2001). Ocean engineering researchers
have studied sea surface statistics and light refrac-
tion (Walker, 1994) as well as numerical modeling of
surface waves (Young, 1999). The vision community
has attempted to study light refraction between water
and materials (Mall and da Vitoria Lobo, 1995), re-
cover water surface geometry (Murase, 1992), as well
as reconstruct images of submerged objects (Efros
et al., 2004; Shefer et al., 2001). In this paper, we
focus on the problem of recovering images with min-
imum distortion.
A simple approach to the reconstruction of images
of submerged objects is to perform a temporal av-
erage of a large number of continuous video frames
acquired over an extended time duration (i.e., mean
value of each pixel over time) (Shefer et al., 2001).
This technique is based on the assumption that the
integral of the periodic function modeling the water
waves is zero (or constant) when time tends to in-
finity. Average-based methods such as the one de-
scribed in (Shefer et al., 2001) can produce reason-
able results when the distortion is caused by low en-
ergy waves (i.e., waves of low amplitude and low fre-
quency). However, this method does not work well
when the waves are of higher energy, as averaging
over all frames equally combines information from
both high and low distortion data. As a result, the av-
eraged image will appear blurry and the finer details
will be lost.
Modeling the three-dimensional structure of the
waves also provides a way to solve the image recov-
ery problem. Murase (Murase, 1992) approaches the
problem by first reconstructing the 3D geometry of
the waves from videos using optical flow estimation.
He then uses the estimated optical flow field to cal-
culate the water surface normals over time. Once the
surface normals are known, both the 3D wave geom-
etry and the image of submerged objects are recon-
structed. Murase’s algorithm assumes that the water
depth is known, and the amplitude of the waves is low
enough that there is no separation or elimination of
features in the image frames. If these conditions are
not met, the resulting reconstruction will contain er-
rors mainly due to incorrect optical flow extraction.
More recently, Efros et al. (Efros et al., 2004)
proposed a graph-based method that attempts to re-
cover images with minimum distortion from videos
of submerged objects. The main assumption is that
the underlying distribution of local image distortion
due to refraction is Gaussian shaped (Cox and Munk,
1956). Efros et al., propose to form an embedding of
subregions observed at a specific location over time
and then estimate the subregion that corresponds to
the center of the embedding. The Gaussian distor-
tion assumption implies that the local patch that is
closer to the mean is fronto-parallel to the camera and,
as a result, the underwater object should be clearly
observable through the water at that point in time.
The solution is given by selecting the local patches
that are the closest to the center of their embedding.
Efros et al., propose the use of a shortest path al-
gorithm that selects the solution as the frame hav-
ing the shortest overall path to all the other frames.
Distances were computed transitively using normal-
ized cross-correlation (NCC). Their method addresses
likely leakage problems caused by erroneous shortest-
distances between similar but blurred patches by cal-
culating paths using a convex flow approach. The
sharpness of the image reconstruction achieved by
their algorithm is very high compared to average-
based methods even when applied to sequences dis-
torted by high energy waves.
In this paper we follow Efros et al. (Efros et al.,
2004), considering an ensemble of fixed local regions
over the whole video sequence. However, our method
differs from theirs in two main ways. First, we pro-
pose to reduce the leakage problem by addressing the
motion blur effect and the refraction effect separately.
Second, we take a frequency domain approach to the
problem by quantifying the amount of motion blur
present in the local image regions based on measure-
ments of the total energy in high frequencies.
Our method aims at improving upon the basic
average-based techniques by attempting to separate
image subregions into high and low distortion groups.
The K-Means algorithm (Duda et al., 2000) is used
along with a frequency domain analysis for generat-
ing and distinguishing the two groups in terms of the
quality of their member frames. Normalized cross-
correlation is then used as a distance measurement to
IMPROVED RECONSTRUCTION OF IMAGES DISTORTED BY WATER WAVES
229
find the single frame that best represents the undis-
torted view of the region being analyzed.
3 DISTORTION ANALYSIS
In the problem considered in this paper, the local im-
age distortions caused by random surface waves can
be assumed to be modeled by a Gaussian distribu-
tion (Efros et al., 2004; Cox and Munk, 1956). The
magnitude of the distortion at a given image point in-
creases radially, forming a disk in which the center
point contains the least amount of distortion. The cen-
ter subregion can be determined by a clustering algo-
rithm if the distribution of the local patches is not too
broad (i.e., the diameter of the disk is small) (Efros
et al., 2004). Our method effectively reduces the size
of this distortion embedding by removing the sub-
regions containing large amounts of translation and
motion blur. In this section, we analyze how refrac-
tion and motion blur interferes with the appearance of
submerged objects observed from outside the water.
First, we analyze the geometry of refraction and its
relationship to both the surface normals of the waves
and the distance from the camera to the water. We
then analyze the motion blur distortion caused by the
speed of oscillation of the waves, and how it can be
quantified in the frequency domain.
3.1 Refraction Caused by Waves
Consider a planar object submerged in shallow trans-
parent water. The object is observed from a static
viewpoint above the water by a video camera with
optical axis perpendicular to the submerged planar
object. In our modeling, we assume that only the
water is moving in the scene (i.e., both the camera
and the underwater object are stationary). Addition-
ally, the depth of the object is assumed to be unknown
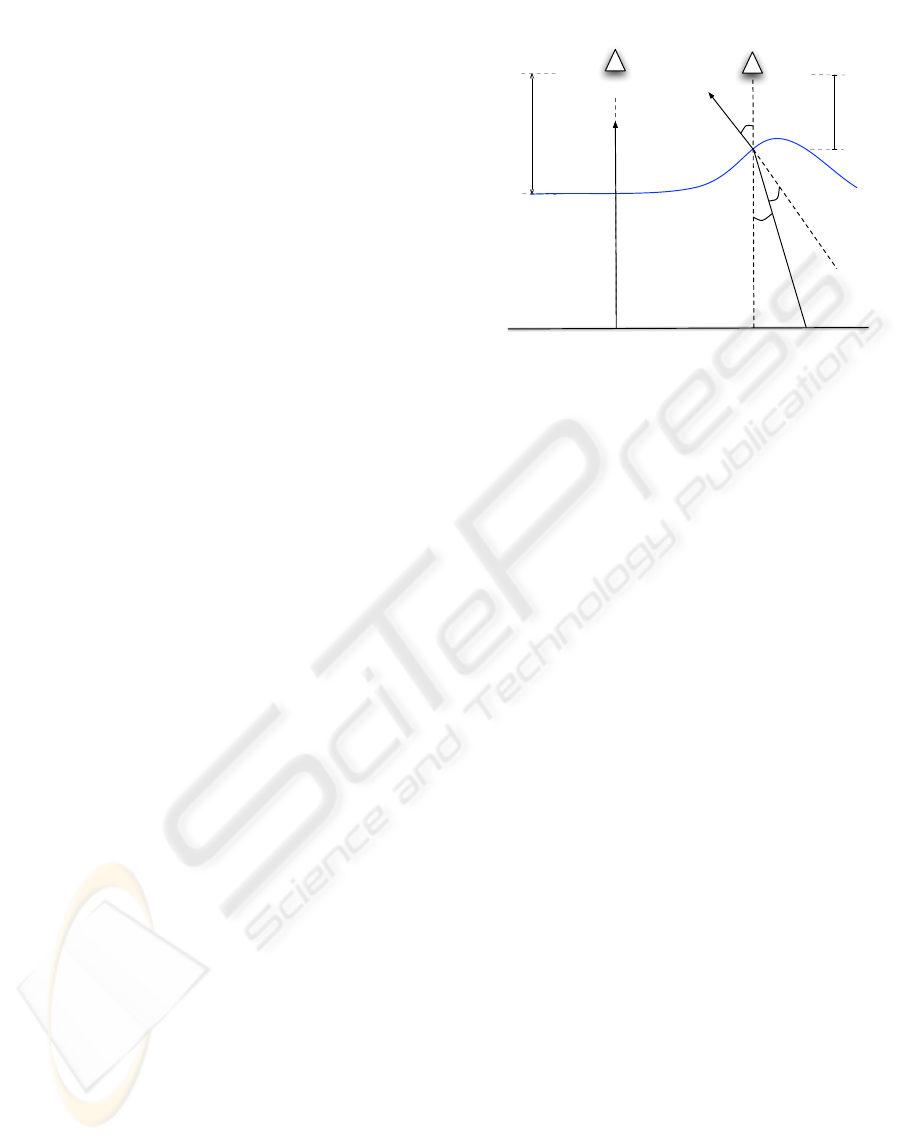
and constant. Figure 2 illustrates the geometry of the
scene. In the figure, d is the distance between the
camera and a point where the ray of light intersects
the water surface (i.e., point of refraction). The an-
gle between the viewing ray and the surface normal is
θ
n
, and the angle between the refracted viewing ray
and the surface normal is θ
r
. These two angles are
related by Snell’s law (1). The camera c observes a
submerged point p. The angle α measures the rela-
tive translation of the point p when the viewing ray is
refracted by the water waves.
According to the diagram in Figure 2, the image
seen by the camera is distorted by refraction as a func-
tion of both the angle of the water surface normal at
the point of refraction and the amplitude of the water
waves. If the water is perfectly flat (i.e., there are no
waves), there will be no distortion due to refraction.
n
c
p = p'
d
time = t
ϴ
ϴ
n
r
n
c
p p'
d
time = t + 1
o
o
Figure 2: Geometry of refraction on a surface disturbed by
waves. The camera c observes a given point p on the sub-
merged planar object. The slant angle of the surface normal
(θ
n
) and the distance from surface to the camera (d) are the
main parameters of our distortion model. When θ
n
is zero,
the camera observes the point p at its original location on
the object (i.e., there is no distortion in the image). If θ
n
changes, the apparent position of p changes by a transla-
tion factor with magnitude kp
0
− pk. This magnitude also
varies as a function of the distance from the water surface
to the camera (e.g., due to the amplitude of the waves). The
figure also illustrates the light refracting with the waves at
two different points in time. The image at time t would ap-
pear clear while the image at time t+1 would be distorted by
refraction.
However, if the surface of the water is being disturbed
by waves, the nature of the image distortion becomes
considerably more complex. In this paper, we will fo-
cus on the case where the imaged object is planar and
is parallel to the viewing plane (i.e., the planar object
is perpendicular to the optical axis of the camera).
In the experiments described in this paper, the main
parameters that model the spatial distortion in the im-
age are the slant angle of the surface normal (θ
n
) and
the distance from surface to the camera (d). The two
parameters affect the image appearance by translating
image pixels within a small local neighborhood. More
specifically, the varying slope of the waves and their
amplitude will modify the angle of refraction that will
result in the distortion of the final image. Addition-
ally, considerable motion blur can occur in each video
frame due to both the limited capture frequency of
the video system, and the dynamic nature of the liq-
uid surface. The blur will have different magnitudes
across the image in each video frame. In our experi-
ments, varying levels of motion blur will be present in
each frame depending on the speed of change in the
slant of the surface normals. Next, we show that the
translation caused by refraction is linear with respect
VISAPP 2006 - IMAGE ANALYSIS
230

to the distance d and non-linear with respect to the
slant angle of the water surface normal (θ
n
).
We commence by modeling the refraction of the
viewing ray. The refraction of light from air to water
is given by Snell’s law as:
sin θ
n
= r
w
sin θ
r
(1)
where θ
n
is the angle of incidence of light. In our
case, θ
n
corresponds to the slant angle of the wa-
ter surface normal. θ
r
is the angle of refraction be-
tween the surface normal and the refracted viewing
ray. The air refraction coefficient is assumed to be
the unit and r
w
is the water refraction coefficient (r
w
= 1.33). From Figure 2, the angle that measures the
amount of translation when θ
n
varies is given by:
α = θ
n
− θ
r
(2)
Solving for θ
r
in Equation 1 and substituting the re-
sult into Equation 2 we have:
α = θ
n
− arcsin(
sin θ
n
r
w
) (3)
Considering the triangle 4opp
0
, the magnitude of the
underwater translation is given by:
kp
i
− pk = d tan α (4)
From (3), the overall translation is:
kp
i
− pk = d tan[θ
n
− arcsin(
sin θ
n
r
w
)] (5)
Equation 5 describes the translational distortion of
underwater points caused by two parameters: the slant
angle of the surface normal and the distance between
the camera and the point of refraction. The magnitude
of translation in (5) is linear with respect to d and non-
linear with respect to θ
n
. These two variables will
vary according to the movement of the water waves.
For a single sinusoidal wave pattern model, the am-
plitude of the wave will affect d while the slope of
the waves will affect the value of θ
n
. The distortion
modeled by Equation 5 vanishes when d = 0 (i.e., the
camera is underwater), or the angle θ
n
is zero (i.e., the
surface normal is aligned with the viewing direction).
3.2 Motion Blur and Frequency
Domain
Motion blur accounts for a large part of the distortion
in videos of submerged objects when the waves are of
high energy. The speed of oscillation of the surface
waves causes motion blur in each frame due to lim-
ited video frame rate. Studies have shown that an in-
crease in the amount of image blur decreases the total
high frequency energy in the image (Field and Brady,
1997).
Figure 3: Blur and its effect on the Fourier domain. Top
row: images with increasing levels of blur. Bottom row:
corresponding radial frequency histograms. Blur causes a
fast drop in energy in the radial spectral descriptor (decrease
in high frequency content).
Figure 3 shows some examples of regions with mo-
tion blur distortion (top row) and their corresponding
radial frequency histograms after a high-pass filter is
applied to the power spectrum (bottom row). The de-
crease of energy in high frequencies suggests that, in
principle, it is possible to determine the level of blur
in images of the same object by measuring the total
energy in high frequencies.
As pointed out in (Field and Brady, 1997), mea-
suring the decay of high-frequency energy alone does
not work well for quantifying motion blur of differ-
ent types of images, as a simple reduction of the to-
tal number of edges in an image will produce power
spectra with less energy in higher frequencies but no
decrease in the actual image sharpness. Alternatively,
blur in images from different scenes can be more ef-
fectively quantified using measures such as the phase
coherence described in (Wang and Simoncelli, 2004).
In this paper, we follow (Field and Brady, 1997) by
using a frequency domain approach to quantify the
amount of motion blur in an image. We use the to-
tal energy of high-frequencies as a measure of image
quality. This measurement is able to accurately quan-
tify relative blur when images are taken from the same
object or scene (e.g., images roughly containing the
same number of edges).
In order to detect the amount of blur present in a set
of images corresponding to the same region of the ob-
ject, we first apply a high-pass filter to the power spec-
trum of each image. We express the filtered power
spectrum in polar coordinates to produce a function
S(r, θ), where S is the spectrum function, r and θ
are the variables in this coordinate system. A global
description of the spectral energy can be obtained
by integrating the the polar power spectrum function
into 1D histograms as follows (Gonzalez and Woods,
1992):
S(r) =
π
X
θ=0
S(r, θ) (6)
IMPROVED RECONSTRUCTION OF IMAGES DISTORTED BY WATER WAVES
231

Summing the high-frequency spectral energy in the
1D histograms provides us with a simple way to de-
termine changes in the level of blur when comparing
blurred versions of the same image. Figure 3 (bottom
row) shows a sample of radial frequency histograms.
The low frequency content in the histograms has been
filtered out by the high-pass filter. The decrease in the
high-frequency energy corresponds to an increase on
the level of motion blur in the images.
4 METHOD OVERVIEW
Let us assume that we have a video sequence with
N frames of a submerged object. We commence
by sub-dividing all the video frames into K small
overlapping sub-regions (R
k
= {x
1
, . . . , x
N
}, k =
1, . . . , K). The input data of our algorithm consists
of these K sets of smaller videos describing the lo-
cal refraction distortion caused by waves on the ac-
tual large image. The key assumption here is that lo-
cal regions will sometimes appear undistorted as the
surface normal of the local plane that contains the re-
gion is aligned with the optical axis of the camera.
Our goal is to determine the local region frame in-
side each region dataset that is closest to that fronto-
parallel plane. We approach the problem by assuming
that there will be two main types of distortion in the
local dataset. The distortions are described in Sec-
tion 3. The first type is the one caused by pure refrac-
tion driven by changes in both distance from the cam-
era to the water and the angle of the water surface nor-
mal. The second type of distortion is the motion blur
due to the speed of oscillation of the waves. Refrac-
tion and blur affect the local appearance of the frames
in distinct ways. The first causes the local regions
to translate across neighboring sub-regions while the
second causes edges to become blurred. The exact in-
terplay between these two distortions is complex. The
idea in our algorithm is to quantify these distortions
and select a reduced set of high-quality images from
which we will choose the best representative region
frames.
We start by clustering each local dataset into groups
with the K-Means algorithm (Duda et al., 2000), us-
ing the Euclidean distance between the frames as a
similarity measure. Since no previous knowledge of
the scene is available, the K-Means centers were ini-
tialized with a random selection of sample subregions
from the dataset. The clustering procedure mainly
separates the frames distorted by translation. We ex-
pect the frames with less translation distortion to clus-
ter together. However, some of the resulting clus-
ters will contain frames with motion blur. In our ex-
periments, the Euclidean distance measurement has
shown good results in grouping most, if not all, of the
Algorithm 1 Multi-stage clustering.
Given N video frames:
1: Divide frames into K overlapping sub-regions.
2: Cluster each set of sub-regions to group the low
distortion frames.
3: Remove the images with high level of blur from
each group of low distortion frames.
4: Select the closest region to all other regions in
that set using cross-correlation.
5: Create a final reconstructed single large image by
mosaicking all subregions.
6: Apply a blending technique to reduce tiling arti-
facts between neighboring regions.
lower distortion frames together, with some high dis-
tortion frames present. The initial number of clusters
is very important. We found that the more clusters
we could successfully split a data set into, the easier
it was for the rest of the algorithm to obtain a good
answer. To guarantee convergence, re-clustering was
performed when one of the clusters had less than 10%
of the total number of frames (e.g., in an 80-frame
data set, each of the four clusters must have at least
eight frames or we re-cluster the data). The algorithm
initially attempts to divide the data into 10 clusters. If
each cluster does not contain at least 10% of the total
number of frames after a certain number of iterations,
we reduce the number of clusters by one and repeat
the process until the data is successfully clustered.
We assume that one of the resulting clusters pro-
duced by the K-Means algorithm contains mostly low
distortion frames. To distinguish it from the other
clusters, we take a statistical approach by assuming
that the cluster containing most of the low distortion
frames has the least amount of pixel change across
frames. This is equivalent to saying that the frames
should be similar in appearance to each other. We
compute the variance of each pixel over all frames in
the cluster using
σ
2
=
1
n
Σ
n
i=1
(p
i
− ¯p)
2
(7)
where n is the number of frames in the cluster, p
i
is
the pixel value of the i-th image frame for that point,
and ¯p is the mean pixel value for that point over all
frames in the cluster. We take the sum of the vari-
ances of all the pixels for each cluster, and the clus-
ter with the minimum total variance is labeled as the
low distortion group. Our experiments show that this
technique is approximately 95% successful in distin-
guishing the best cluster. The algorithm discards all
frames that are not in the cluster with the lowest total
variance.
At this point, we have greatly reduced the number
of frames for each region. The next step of the al-
gorithm is to rank all frames in this reduced dataset
VISAPP 2006 - IMAGE ANALYSIS
232

with respect to their sharpness. As described in Sec-
tion 3, the Fourier spectrum of frames containing mo-
tion blur tend to present low energy in high frequency.
This allows us to remove the frames with high level of
blur by measuring the decay of high frequency energy
in the Fourier domain. We calculate the mean energy
of all frame regions and discard the ones whose en-
ergy is less than the mean.
Finally, the algorithm produces a subset of frame
regions which are similar in appearance to each other
and have small amounts of motion blur. We then
choose a single frame from this set to represent the
fronto-parallel region. In (Efros et al., 2004), this
was done using a graph theory approach by running
a shortest path algorithm. We take a somewhat sim-
ilar approach, computing the distances between all
the frames via normalized cross-correlation then find-
ing the frame whose distance is the closest to all the
others. This is equivalent to finding the frame clos-
est to the mean of this reduced set of frames. We
then mosaic all sub-regions and use a blending algo-
rithm (Szeliski and Shum, 1997) to produce the final
reconstructed image.
(a) (b) (c)
(d) (e) (f)
Figure 4: (a) S ubregions being compared. (b) Mean of
the 4 resulting clusters, (c) frames belonging to the chosen
sharpest cluster, (d) frames remaining after removing those
with lower high frequency values, (e) final frame choice to
represent subregion, (f) and average over all frames (shown
for comparison).
Figure 4 illustrates the steps for finding the best
frame of each set. The algorithm takes the frames in
each subregion (Figure 4a) and use K-Means to pro-
duce four clusters (Figure 4b). After variance calcu-
lations, the algorithm determined the top-left cluster
of Figure 4b to be the one with the least overall dis-
tortion. The images in this cluster are then ranked in
decreasing order of high-frequency energy and those
frames whose energy is lower than the mean are re-
moved in an attempt to further reduce the dataset. The
remaining frames are shown in Figure 4d. From this
reduced set, normalized cross correlation distances
are computed in an attempt to find the best choice.
Figure 4e shows the output, and Figure 4f shows the
temporal average of the region for comparison.
5 EXPERIMENTS
In this section we present experimental results for
video sequences recorded in the laboratory and in nat-
ural environments. Current experiments show very
promising results.
In the first experiment, we analyze an 80-frame
video sequence (Figure 1). The waves in this data
set were low energy waves, large enough to cause a
considerable amount of distortion, yet small enough
not to cause any significant separation or occlusion of
the submerged object. The level of distortion in this
dataset is similar to the one used in (Murase, 1992).
Our method provides much sharper results when com-
pared to simple temporal averaging. We extracted
the subregions with 50% overlap. A simple blend-
ing process (Szeliski and Shum, 1997) is applied to
reduce the appearance of “tiles” as observed in the fi-
nal reconstructed image. The results can be seen in
Figure 5. As expected, the blending process slightly
reduced the sharpness of the image in some cases due
to the fact that it is a weighted averaging function.
Figure 5: Low-energy wave dataset. (a) Average over all
frames. (b) Output using our method.
The next experiment shows the output of the algo-
rithm when the input video sequence contains waves
of high energy. These waves may occlude or sepa-
rate the underwater object at times, temporarily mak-
ing subregions completely blurry and unrecognizable.
IMPROVED RECONSTRUCTION OF IMAGES DISTORTED BY WATER WAVES
233

Figure 6: High-energy wave dataset. (a) Average over all
frames. (b) Output using our method.
For a few regions of the image, the dataset does not
contain a single frame in which the object is clearly
observed, making it difficult to choose a good frame
from the set. The blur and occlusion complicate the
reconstruction problem, but our algorithm handles it
well by explicitly measuring blur and using it to se-
lect high-quality frames from each cluster. Figure 6
shows our results.
Our final experiments deal with datasets obtained
in a natural outdoor environment. The videos were
acquired from the moving stream of a small creek.
The waves in this dataset are of high energy, but un-
like the previous dataset, these are of low magnitude
but very high frequency and speed, naturally gener-
ated by the creek’s stream. Figures 7 and 8 show our
results.
6 CONCLUSIONS
We propose a new method for recovering images of
underwater objects distorted by surface waves. Our
method provides promising improved results over
computing a simple temporal average. It begins by di-
viding the video frames into subregions followed by a
temporal comparison of each region, filtering out the
low distortion frames via the K-Means algorithm and
frequency domain analysis of motion blur.
In our method, we approach the problem in a way
similar to (Efros et al., 2004) as we perform a tempo-
ral comparison of subregions to estimate the center of
the Gaussian-like distribution of an ensemble of local
subregions. Our approach differs from theirs in two
main aspects. First, we considerably reduce the “leak-
age” problem (i.e., erroneous NCC correlations being
Figure 7: Creek stream data set 1. (a) Average over all
frames. (b) Output using our method.
classified as shortest distances) by clustering the sub-
regions using a multi-stage approach that reduces the
data to a small number of high-quality regions. Sec-
ond, we use frequency-domain analysis that allows us
to quantify the level of distortion caused by motion
blur in the local sub-regions. Our results show that
the proposed method is effective in removing distor-
tion caused by refraction in situations when the sur-
face of the water is being disturbed by waves. A di-
rect comparison between our method and previously
published methods (Efros et al., 2004; Murase, 1992;
Shefer et al., 2001) is difficult due to the varying wave
conditions between data sets, as well as the lack of
a method for quantifying the accuracy of the recon-
struction results.
Working with video sequences that contain high
energy waves is a complex task due to occlusion and
blurriness introduced into the image frames. Our al-
gorithm handles these conditions well by explicitly
measuring blur in each subregion. Additionally, large
energy waves introduce the problem that a given em-
bedding of subregions may not contain a single frame
corresponding, or near, to a point in time when the
VISAPP 2006 - IMAGE ANALYSIS
234

Figure 8: Creek stream data set 2. (a) Average over all
frames. (b) Output using our method.
water normal is parallel to the camera’s optical axis.
This affects the quality of our results.
Our plans for future research involve extending the
current algorithm to improve results when dealing
with high energy waves. We are currently researching
the incorporation of constraints provided by neigh-
boring patches. These constraints can, in principle,
be added by means of global alignment algorithms.
Further lines of research involve extending the cur-
rent method to use explicit models of both waves and
refraction in shallow water (Gamito and Musgrave,
2002), and the application of our ideas to the problem
of recognizing submerged objects and textures. We
are currently working on developing these ideas and
they will be reported in due course.
ACKNOWLEDGMENTS
The authors would like to thank Dr. Alexey Efros
for kindly providing us with an underwater video se-
quence which we used to initially develop and test our
algorithm.
REFERENCES
Cox, C. and Munk, W. (1956). Slopes of the sea surface
deduced from photographs of the sun glitter. Bull.
Scripps Inst. Oceanogr., 6:401–488.
Duda, R. O., Hart, P. E., and Stork, D. G. (2000). Pattern
Classification (2nd Edition). Wiley-Interscience.
Efros, A., Isler, V., Shi, J., and Visontai, M. (2004). See-
ing through water. In Saul, L. K., Weiss, Y., and
Bottou, L., editors, Advances in Neural Info rmation
Processing Systems 17, pages 393–400. MIT Press,
Cambridge, MA.
Field, D. and Brady, N. (1997). Visual sensitivity, blur and
the sources of variability in the amplitude spectra of
natural scenes. Vision Research. Dec;37(23):3367-
83., 37(23):3367–3383.
Gamito, M. N. and Musgrave, F. K. (2002). An accurate
model of wave refraction over shallow water. Com-
puters & Graphics, 26(2):291–307.
Gonzalez, R. C. and Woods, R. E. (1992). Digital Image
Processing. Addison-Wesley, Reading, MA.
Mall, H. B. and da Vitoria Lobo, N. (1995). Determining
wet surfaces from dry. In ICCV, pages 963–968.
Murase, H. (1992). Surface shape reconstruction of a non-
rigid transparent object using refraction and motion.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, 10(10):1045–1052.
Premoze, S. and Ashikhmin, M. (2001). Rendering natural
waters. Computer Graphics Forum, 20(4).
Shefer, R., Malhi, M., and Shenhar, A. (2001).
Waves distortion correction using cross corre-
lation. (http://visl.technion.ac.il/projects/2000maor/).
http://visl.technion.ac.il/projects/2000maor/.
Szeliski, R. and Shum, H.-Y. (1997). Creating full view
panoramic image mosaics and environment maps. In
SIGGRAPH ’97: Proceedings of the 24th annual con-
ference on Computer graphics and interactive tech-
niques, pages 251–258, New York, NY, USA. ACM
Press/Addison-Wesley Publishing Co.
Walker, R. E. (1994). Marine Light Field Statistics. John
Wiley & Sons.
Wang, Z. and Simoncelli, E. P. (2004). Local phase coher-
ence and the perception of blur. In Thrun, S., Saul,
L., and Sch
¨
olkopf, B., editors, Advances in Neural In-
formation Processing Systems 16. MIT Press, Cam-
bridge, MA.
Young, I. R. (1999). Wind Generated Ocean Waves. Else-
vier.
IMPROVED RECONSTRUCTION OF IMAGES DISTORTED BY WATER WAVES
235
