HIERARCHICAL ESTIMATION OF IMAGE FEATURES WITH
COMPENSATION OF MODEL APPROXIMATION ERRORS
Stefano Casadei
71 rue du Cardinal Lemoine, 75005 Paris, France
Keywords:
Model-based estimation, edge and corner detection, feature extraction, grouping, feedback, model hierarchy.
Abstract:
To facilitate the optimal estimation of the parameters of a complex image feature, the feature’s model is
fragmented into simpler approximating models. By repeating this fragmentation procedure recursively, a
hierarchy of feature models is obtained. To ensure that feature parameter values are recovered exactly in
the limit of high SNR, an algorithm is proposed to compensate for the model approximation errors between
adjacent levels of the hierarchy.
1 INTRODUCTION
The detection of local image features, such as edges,
corners and junctions, and the estimation of the as-
sociated parameters provide the basis for many com-
puter vision algorithms and systems. One approach
to carry out this task is to process the input image in
a feedforward way, constructing a hierarchy of fea-
tures in a bottom-up order (Marr, 1982; Nalwa and
Binford, 1986; Canny, 1986; Perona, 1995; Casadei
and Mitter, 1999a; Casadei and Mitter, 1998; Casadei
and Mitter, 1999b; Casadei and Mitter, 1996; K
¨
othe,
2003; W
¨
urtz and Lourens, 1997). To improve accu-
racy and to extend the applicability of the basic feed-
forward operators designed for straight-line edges,
some methods analyze the response of these operators
to more complex features, such as lines and corners
(Deriche and Giraudon, 1990; Deriche and Giraudon,
1993; Steger, 1998).
A rather different approach for feature estimation
is model-based optimization, which yields, in prin-
ciple, optimal estimates for all feature parameters.
Direct comparisions with feedforward methods have
shown the superior accuracy and detection perfor-
mance of optimization methods (Rohr, 1992; De-
riche and Blaszka, 1993; Blaszka and Deriche, 1994b;
Blaszka and Deriche, 1994a; Nayar et al., 1996;
Baker et al., 1998).
A key element of optimization methods is the use
of feedback loops to refine feature parameter esti-
mates and to validate feature hypotheses. Typically,
these feedback loops are obtained by using a paramet-
ric feature model to generate image-level reconstruc-
tions of feature hypotheses and by comparing these
reconstructions with the input data.
A disadvantage of many existing model-based op-
timization methods, which are usually based on non-
linear iterative techniques such as the Levenberg-
Marquardt algorithm, is their high computational re-
quirements. Two other difficult aspects of optimiza-
tion methods are parameter initialization and selec-
tion of the estimation window. These problems can be
addressed by representing complex features at multi-
ple levels of complexity and by integrating bottom-
up feedforward processing with top-down feedback
loops. By using of a hierarchy of feature models,
bootstrapping methods can be used to initialize the
parameters of complex features and more computa-
tionally efficient feedback loops (based, for example,
on lookup tables) can be implemented.
The paper is organized as follows. Section 2 ex-
plains the role played by intermediate features in fa-
cilitating top-down model-based feedback and intro-
duces the key definitions underlying the proposed
methodology, which is based on fragmenting com-
plex feature models into simpler approximating mod-
els and on compensating for the model discrepancies
associated with this fragmentation (see Fig. 1). Sec-
tion 3 illustrates this general methodology with an
edge detection example where a corner model is frag-
mented into straight-line edge models. Section 4 de-
scribes a particular algorithm for model discrepancy
compensation.
381
Casadei S. (2006).
HIERARCHICAL ESTIMATION OF IMAGE FEATURES WITH COMPENSATION OF MODEL APPROXIMATION ERRORS.
In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 381-388
DOI: 10.5220/0001369003810388
Copyright
c
 SciTePress

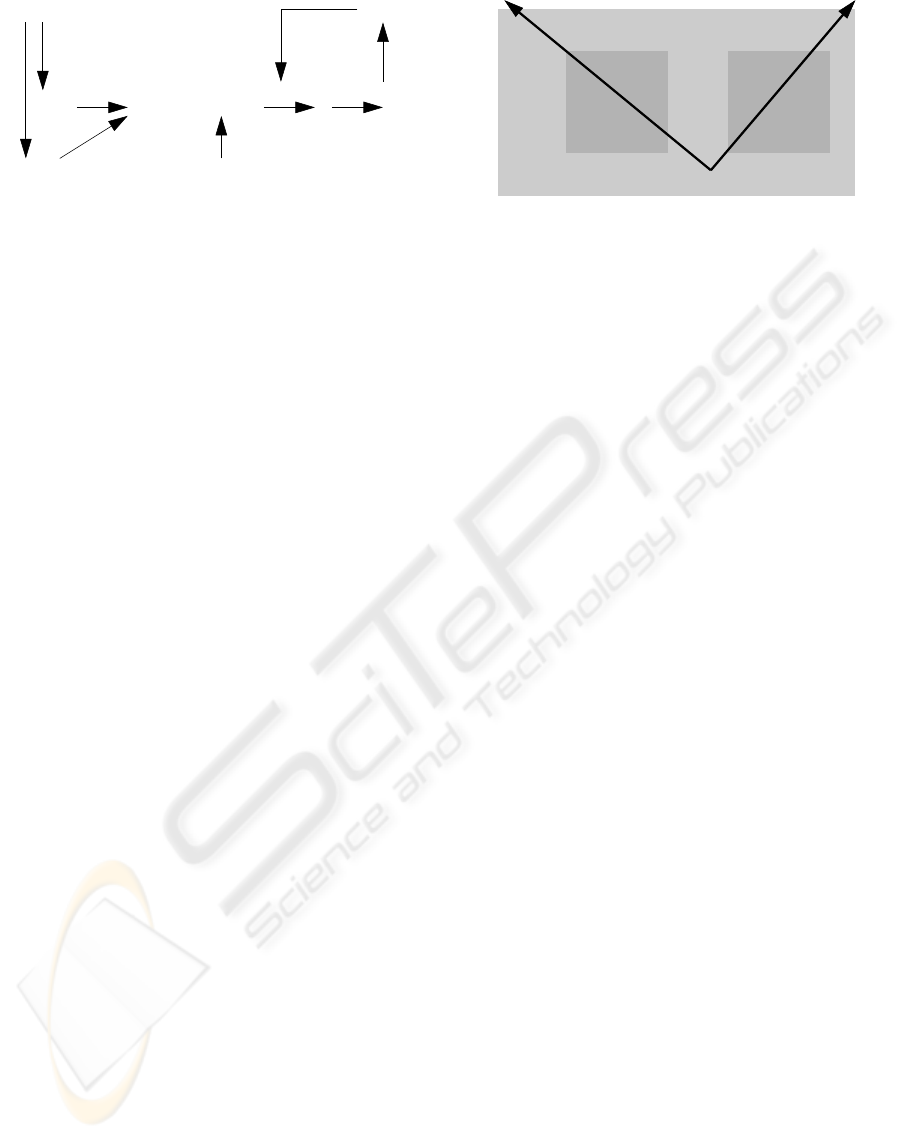
ϑ
I = H(ϑ)+ν
f
f
λ
−1
r(ϑ)+η
π
R|
ˆ
ϑ
ϕ
∗
H(ϑ)
λ
ˆ
ϑ
µ
˜r
−1
r(ϑ)
˜r
λ(ϑ)
H
Figure 1: Feature estimation with an intermediate layer of
auxiliary features. A high-level feature ϑ ∈ Θ is repre-
sented at the image level by a parametric model function
H. The same feature is represented at an intermediate level
by one or more approximating fragments, denoted λ(ϑ).
Centered estimators f for the fragments are provided which
recover the intermediate feature parameters exactly in the
limit of infinite SNR. The distortion map ˜r (see (11)) de-
scribes the effect of the discrepancy (1) between the high
level feature model H and the intermediate feature models
F
k
. The right part of the diagram describes the estimation
process, which begins with an input image I containing a
feature instance plus noise ν. The noisy intermediate fea-
tures recovered by f are r(ϑ)+η. These are projected on
R  r(Θ) according to a metric based on an estimate
ˆ
ϑ
of ϑ (see Appendix B). The result, ϕ
∗
is then compensated
for model discrepancy by inverting the distortion map ˜r. Fi-
nally, an (updated) estimate
ˆ
ϑ is obtained through λ
−1
and
a new iteration is performed.
2 INTERMEDIATE FEATURES
Parametric feature models The proposed method
for feature estimation is illustrated by the diagram in
Fig. 1, which depicts a pair of adjacent levels of a
model hierarchy and the bottom image layer. The top
layer contains the high-level feature to be estimated,
represented by a multi-dimensional feature parameter
ϑ ∈ Θ. A parametric model function, denoted H,
specifies the noiseless or ideal image level represen-
tation of this high-level feature. Specifically, for any
feature parameter ϑ ∈ Θ, H(p; ϑ) denotes the noise-
less value of the feature identified by ϑ at the image
point p ∈ R
2
. The block of feature values associated
with a finite set of image points U ⊂ R
2
is denoted
H(U; ϑ). The input image is denoted I and the image
block associated with the image region U is denoted
I(U).
Model fragmentation An approach to construct a
model hierarchy is to decompose or fragment a fea-
ture instance (ϑ, U), identified by the feature para-
meter ϑ ∈ Θ and the image domain or support U ⊂
R
2
, into one or more intermediate features (ϕ
k
, S
k
),
k =1,...,K, having feature parameters ϕ
k
∈ Φ
k
,
image domains S
k
⊂ U, and image representations
F
k
(S
k
; ϕ
k
), where F
k
are the parametric model func-
ψ
2
U q
L
2
b + a
b − a
b − a
L
1
ψ
1
S
1
S
2
Figure 2: Fragmentation of a corner feature H(U; ϑ) into
two straight-line edge features F (S
1
; ϕ
1
) and F (S
2
; ϕ
2
).
tions of the intermediate features. For example, a cor-
ner feature can be decomposed into two straight-line
features as described by (19), (20) and as shown in
Fig. 2.
Model fragmentation is carried out so that
F
k
(S
k
; ϕ
k
), k =1,...,K, are local approximations
of H(U; ϑ). The associated approximation error is
referred to as model discrepancy and is denoted ∆
k
.
For any ϑ ∈ Θ, and for a particular configuration of
the domains U and S
k
, let λ
k
(ϑ) ∈ Φ
k
be the model
parameter ϕ
k
chosen by the fragmentation procedure
to be the local approximator of the k-th fragment.
Then, the k-th model discrepancy is given by:
∆
k
(ϑ)  H(S
k
; ϑ) − F
k
(S
k
; λ
k
(ϑ)). (1)
Generally speaking, our strategy to design accu-
rate and computationally efficient feature estimators
is to construct hierarchical fragmentations of a com-
plex models into intermediate approximating models,
so that the model discrepancy between adjacent levels
of the hierarchy is sufficiently small to guarantee the
effectiveness and computational efficiency of model-
based feedback loops.
Local parametrization The functions λ
k
:Θ→
Φ
k
associated with a model fragmentation provide
a “local” parametrization for the fragmented H-
features. Indeed, model fragmentations are typically
constructed so that the joint coordinate map:
λ :Θ→ Φ  Φ
1
×···×Φ
K
(2)
given by
λ(ϑ)=(λ
1
(ϑ),...,λ
K
(ϑ)), (3)
is injective. Thus, by letting λ(Θ) ⊂ Φ be the image
of Θ under λ, which is also the set of all “consistent”
combinations of local coordinates:
λ(Θ) = {(ϕ
1
,...,ϕ
K
), ∃ϑ ∈ Θ,λ
k
(ϑ)=ϕ
k
},
(4)
one obtains the bijective coordinate map
λ :Θ→ λ(Θ), (5)
which yields a local reparametrization of the feature
model H.
VISAPP 2006 - IMAGE ANALYSIS
382

Feature estimators Let us assume that estimators
for the intermediate features are given and are repre-
sented by the maps:
f
k
: R
S
k
→ Φ
k
,k=1,...,K. (6)
That is, for a given input image I and a given image
domain S
k
, the estimated parameter of the interme-
diate feature is f
k
(I(S
k
)), where I(S
k
) is the image
block with domain S
k
.
An estimator is said to be centered if it recovers the
exact value of the feature parameter when the image
contains a noiseless instance of the feature. That is,
f
k
is centered if
f
k
(F
k
(S
k
; ϕ
k
)) = ϕ
k
, ∀ϕ
k
∈ Φ
k
. (7)
Note that the property of being centered is relative
to a particular feature model. For example, Canny’s
edge detector is centered only for edges with zero
curvature (see (Deriche and Giraudon, 1990; Deriche
and Giraudon, 1993; Steger, 1998) and Fig. 6). In
general, feedforward estimators are centered only for
very simple feature models. An objective of the pro-
posed method is to construct centered estimators for
complex feature models by using feedback and hier-
archical representations.
Hierarchical feedback loops In a standard, non-
hierarchical model-based approach for feature esti-
mation, a feedback loop is obtained by comparing an
input image block I(U) with the image representa-
tion H(U;
ˆ
ϑ) of the current feature estimate
ˆ
ϑ. The
error signal ||I(U) − H(U;
ˆ
ϑ)|| and its derivatives
are used iteratively to obtain better feature estimates,
for example, through gradient descent, Gaussian-
Newton, or Levenberg-Marquardt methods.
In a model-based hierarchical approach, feedback
loops, rather than connecting directly high-level com-
plex features to their image level representations, are
mediated through one or more layers of intermediate
features. One type of feedback loop, which can be
used to compensate for model discrepancies and the
mutual interference between nearby features, is ob-
tained by comparing high-level predictions of the in-
termediate features with low-level predictions of the
same intermediate features. Specifically, the high
level predictions, denoted r
k
(ϑ), are obtained by ap-
plying the estimators f
k
, k =1,...,K to the high-
level model H(U; ϑ):
r
k
(ϑ)=f
k
(H(S
k
; ϑ)) (8)
or, more compactly,
r(ϑ)=f(H(U; ϑ)), (9)
where
f =(f
1
,...,f
K
),
r =(r
1
,...,r
K
),
(10)
and f
k
(H(U; ϑ)) = f
k
(H(S
k
; ϑ)).
The low-level predictions are obtained by applying
the estimators f
k
to the feature models F
k
, to yield
f
k
(F
k
(S
k
; λ
k
(ϑ))). By assuming that f
k
are cen-
tered estimators for the parametric models F
k
(or by
designing them to be so), the low-level prediction of
the k-th intermediate feature is simply λ
k
(ϑ) and the
joint low-level prediction is λ(ϑ). Note that to each
low-level prediction µ ∈ λ(Θ) there corresponds one
high-level prediction given by the map:
˜r : λ(Θ) → r(Θ)
˜r(µ)=f(H(U; λ
−1
(µ))).
(11)
This map describes the distortion in the intermedi-
ate feature parameter due to model discrepancy. In-
deed, notice that if all the model discrepancies ∆
k
(ϑ)
vanish then ˜r is the identity map.
By assuming that the map r is injective, it follows
that ˜r is bijective. Then the inverse ˜r
−1
exists and
can be used to compensate for model discrepancy, as
described in Section 4.
Parameter displacements If the space Φ in which
both λ(Θ) and r(Θ) are embedded is linear, then one
can represent the distortion map ˜r by means of the
parameter displacement map:
s(µ)  ˜r(µ) − µ, µ ∈ λ(Θ), (12)
which represents the error in predicting the intermedi-
ate features due to the discrepancy between the high-
level “integrated” model H and the elementary mod-
els F
k
. A more general definition (for the case where
the estimators f are not necessarily centered) is given
by:
s
k
(ϑ)  f
k
(H(S
k
; ϑ)) − f
k
(F
k
(S
k
; λ
k
(ϑ))). (13)
The parameter displacements can be learnt during
an offline setup stage by simulating the estimators f
on the appropriate feature instances. They can then
stored in a memory and accessed through a lookup
table during the image processing stage to compen-
sate for model discrepancies, as described in Section
4. Fig. 3 illustrates the parameter displacements due
to the discrepancy between a corner feature model and
a straight-line edge model.
3 EDGE DETECTION
3.1 A Hierarchy of Edge Models
The model hierarchy of the edge detector we have de-
veloped contains first order (P1) and third order (P30)
polynomial models, blurred straight-line edges (SE)
HIERARCHICAL ESTIMATION OF IMAGE FEATURES WITH COMPENSATION OF MODEL APPROXIMATION
ERRORS
383

0 1 2 3
0
.05
0.1
0
.15
0.2
0
.25
0.3
Orientation
0 1 2 3
−0.6
−0.5
−0.4
−0.3
−0.2
−0.1
Position
0 1 2 3
0
0.005
0.01
0.015
0.02
0.025
0.03
Scale
0 1 2 3
−0.14
−0.12
−0.1
−0.08
−0.06
−0.04
−0.02
0
Stepsize
0 1 2
3
−0.04
−0.02
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
Offset
Figure 3: Parameter displacement of an SE feature due to
the discrepancy with a corner feature. The x-axis represents
the distance between the vertex of the corner point q and
the edge-line center q
k
of the SE feature (see Fig. 5). Each
curve is for a given value of the bending angle β, ranging
between 0 and π/2. From left to right are the displacement
of orientation and position of L
2
; σ, a and b. The value of
a is 1.
and corners (Co). The parametric model functions for
the three lowest levels are given by:
H
P1
(p; ϑ
P1
)=b + aX
ψ
(p), (14)
H
P30
(p; ϑ
P30
)=b +
3
2
a
σ
X
L
(p) −
a
2σ
3
X
L
(p)
3
,
(15)
H
SE
(p; ϑ
SE
)=(b − a)+
2a
√
2π

X
L
(p)
σ
−∞
e
−
t

2
2
dt

,
(16)
where
• ϑ
P1
=(ψ, a, b); L
ψ
is a straight line with ori-
entation ψ orthogonal to the gradient and passing
through a reference point (e.g., the center of the
feature domain); X
ψ
(p) is the signed distance from
this line to the point p;
• ϑ
P30
=(L, a, b, σ); L is a straight line and X
L
(p)
is the signed distance from this line to the point p;
• ϑ
SE
=(L, a, b, σ), where L is the edge line.
Note that H
SE
-features are obtained by blurring step-
edge features with a gaussian filter.
To illustrate the proposed method and the defini-
tions of the previous section, we focus now on the two
layers containing respectively H
SE
-features (playing
the role of intermediate features) and H
Co
-features
(playing the role of high-level features). A common
model for corner features is given by:
H(p; L
1
,L
2
,a,b,σ)=b − a +2aC
σ
(p; L
1
,L
2
),
(17)
where (see Fig. 4, right panel): (L
1
,L
2
,a,b,σ) is
the 7D parameter of corner features, henceforth de-
noted ϑ ∈ Θ; L
1
,L
2
are oriented straight lines in
the image plane forming angles ψ
1
,ψ
2
∈ [0, 2π[,
ψ
1
<ψ
2
with a reference line; b ∈ R is the “as-
ymptotic” image value (as the distance from the cor-
ner point approaches infinity) on the edge lines L
1
C(L
1
,L
2
)
U
L
b − a
b + a
L
2
b + a
−L
1
C(−L, L)
S
b − a
q
ψ
Figure 4: Left: an SE feature with image domain S, rep-
resenting a blurred step edge with image model F (S; ϕ),
as given by (18) or, equivalently, (18). C(−L, L) is the
half-plane lying on the right of L and C(·; −L, L) is its
indicator function. Right: a corner feature with image do-
main U. The cone C(L
1
,L
2
), whose indicator function is
C(·; L
1
,L
2
), lies on the right of the polygonal line obtained
by connecting the lower half of −L
1
with the upper half of
L
2
, as shown. The function C
σ
(·; L
1
,L
2
) is obtained by
convolving C(·; L
1
,L
2
) with a Gaussian filter.
and L
2
; 2a =0is the (signed) image value change
across the edge lines, from the left side to right side;
σ>0 is a blur parameter; C(·; L
1
,L
2
) is the indica-
tor function of the cone C(L
1
,L
2
) delimited by the
lines L
1
,L
2
as shown in Fig. 4; and C
σ
(·; L
1
,L
2
) is
obtained by convolving C(·; L
1
,L
2
) with a Gaussian
filter with variance σ
2
. To facilitate the comparison
between H
SE
-features and H
Co
-features, we rewrite
the former as (see Fig. 4, left panel):
F (p; L, a, b, σ)=b − a +2aC
σ
(p; −L, L). (18)
3.2 Fragmenting Corner Features
A corner feature H(U; ϑ) is decomposed into two
blurred step-edge features F (S
1
; ϕ
1
), F (S
1
; ϕ
2
),
whose domains S
1
and S
2
are roughly bisected by
the two branches of the corner, as shown in Fig. 2.
For any ϑ =(L
1
,L
2
,a,b,σ), the local parameters
λ
1
(ϑ) and λ
2
(ϑ), which characterize the approximat-
ing straight-line edge features, are chosen as follows:
λ
1
(ϑ)=(L
1
, −a, b, σ), (19)
λ
2
(ϑ)=(L
2
,a,b,σ). (20)
With this choice, the discrepancies (1) between the
corner feature and the approximating straight-line
edge features vanish as the distances between S
k
,
k =1, 2 and the corner point q increases.
The parameter displacements of ϕ
2
can be stored in
a lookup table indexed by the parameters L
2
,σ,β,d,
where d is the longitudinal coordinate of the corner
point q along the line L
2
, as shown in Fig. 5, and β is
the deviation of the corner from a straight-line. The
values of these parameter displacements as β and d
vary while L
2
and σ are held fix, are shown in Fig. 3.
VISAPP 2006 - IMAGE ANALYSIS
384

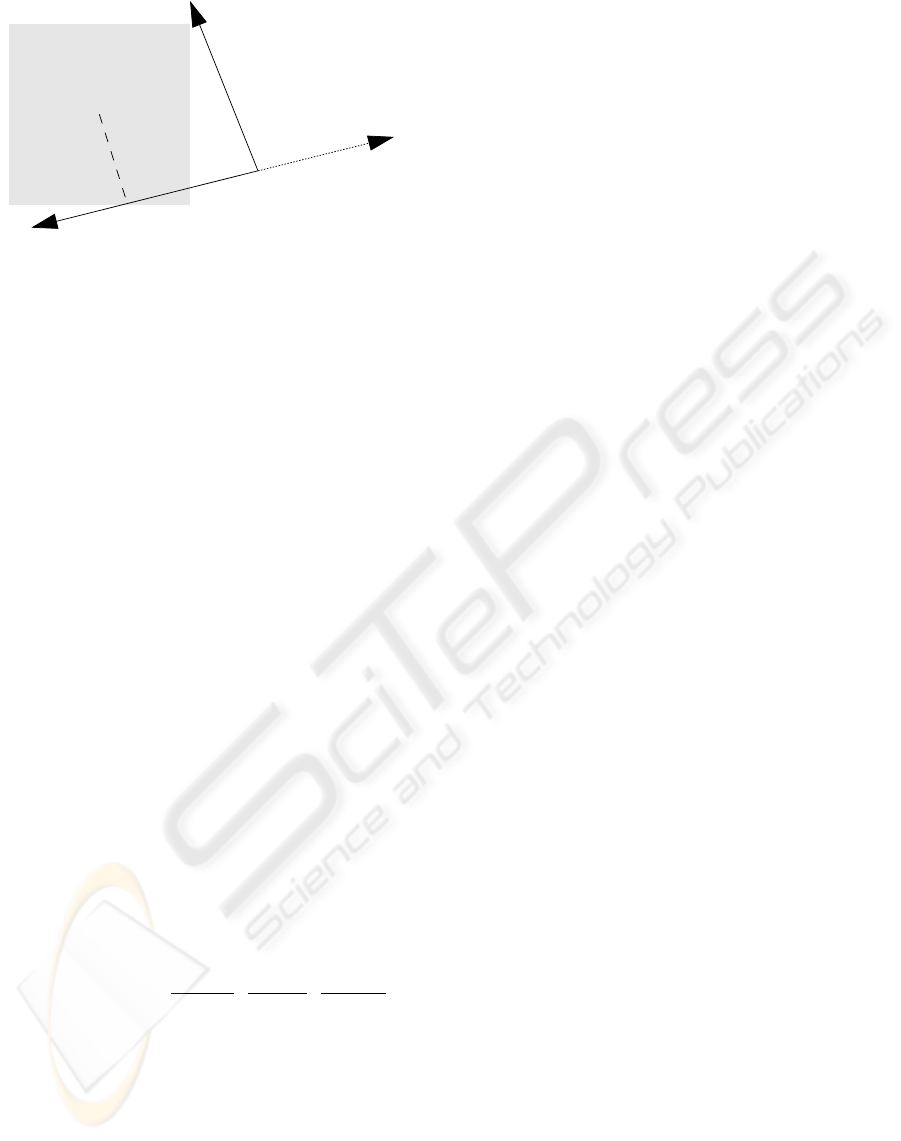
β
q
ψ
1
ψ
2
+ π
−L
2
q
2
S
2
L
2
ψ
2
L
1
Figure 5: The displacement of the SE parameter ϕ
2
(esti-
mated in the domain S
2
) induced by a corner feature with
vertex q and orientations ψ
1
, ψ
2
, depend on the following
variables: the edge line L
2
; the blur parameter σ; the signed
distance from q
2
to q; and the bending angle β, given by
the orientation of L
1
relative to −L
2
, and representing the
deviation of the corner’s polygonal line (−L
1
,L
2
) from a
straight line.
3.3 Grouping Projectors
To utilize model-based feedback, it is necessary to
provide an initial estimate of the high-level model pa-
rameter ϑ. This initial estimate can be obtained from
the local parameter values ϕ =(ϕ
1
,...,ϕ
K
) ∈ Φ
calculated by the estimators f on the input image,
ϕ = f (I(U)). Formally, the operation of mapping
ϕ to an initial estimate for ϑ can be represented by an
operator
π :Φ→ λ(Θ). (21)
The initial estimate for ϑ is then λ
−1
(π(ϕ)). It will
be assumed that a local parameter ϕ that is the local
coordinate λ(ϑ
0
) of some high-level parameter ϑ
0
is
treated by π as such so that π is a projector from Φ to
λ(Θ):
π(µ)=µ, ∀µ ∈ λ(Θ). (22)
In our corner example, the following projector π is
used:
π
k
(ϕ
1
,ϕ
2
)=

s
k
L
k
,
a
1
+ a
2
2
,
b
1
+ b
2
2
,
σ
1
+ σ
2
2

,
(23)
where ϕ
k
=(L
k
,a
k
,b
k
,σ
k
), k =1, 2 and the signs
s
k
are chosen depending on the relative geometric
configuration of L
1
,L
2
, S
1
, S
2
. Notice that this oper-
ator describes the basic grouping operation of form-
ing a corner feature by simply intersecting the two
straight-lines L
1
and L
2
and averaging the other pa-
rameters a
k
, b
k
, and σ
k
. Notice that this simple op-
eration does not yield, in general, the correct value of
the corner feature parameter ϑ in response to a noise-
less corner feature given by (17).
3.4 Estimation Algorithm
A detection algorithm that simultaneously estimates
straight-line edges and corners has been implemented
and the results of an experiment are shown in Fig.
6. The proposed method of fragmenting the feature
model and inverting the associated distortion map ˜r is
utilized twice: once to estimate SE features from P30
features and once to estimate corners from SE fea-
tures. P1 features, calculated from 2x2 image blocks,
are used to provide an initial estimate for edge ori-
entation. P30 features are calculated by least-square
fitting a third order polynomial, varying only in the
direction perpedicular to the initial P1 orientation es-
timate, to all 4x4 image blocks where the P1 image
gradient is above a threshold. SE features are ob-
tained from P30 features by means of a 3D lookup
table that compensates for the SE-P30 discrepancy.
Finally, corner features are obtained by means of the
compensation method described in the next section,
applied to the corner fragmentation (19)-(20).
4 MODEL DISCREPANCY
COMPENSATION
This section describes a method to mitigate the model
discrepancies arising in a hierarchical estimation ap-
proach. Random disturbances, such as additive i.i.d.
noise, the mitigation of which is briefly discussed in
Appendix B, are neglected here. Instead, note that
structured disturbances, such as those caused by the
interference of nearby features, are clearly addressed
by the method described here. Indeed, in a hierar-
chical approach, interference can be compensated for
by introducing a more global, higher level, composi-
tional model comprising the interfering elements and
modeling their mutual interference. For example, a
corner edge model describes the interference between
its two constituent straight-line edges and compen-
sating the discrepancy between corner and straight-
line features amounts to mitigating the interference
between these straight-line features.
To compensate for model discrepancy (and feature
interference) a centered estimator must be constructed
for the high-level feature parameter ϑ. If, by recur-
sion, it is assumed that centered estimators f
k
for the
low-level feature parameters ϕ
k
are available, then a
centered estimator h for ϑ can be obtained by invert-
ing the distortion map ˜r given in (11). More precisely,
let the input image be given by:
I(U)=H(U; ϑ), (24)
and let ϕ
0
be the intermediate feature parameters es-
timated through the estimators f:
ϕ
0
= f(I(U)). (25)
HIERARCHICAL ESTIMATION OF IMAGE FEATURES WITH COMPENSATION OF MODEL APPROXIMATION
ERRORS
385

4 6 8 10 12 14
4
6
8
10
12
14
4 6 8 10 12 14
4
6
8
10
12
14
4 6 8 10 12 14
4
6
8
10
12
14
4 6 8 10 12 14
4
6
8
10
12
14
4 6 8 10 12 14
4
6
8
10
12
14
4 6 8 10 12 14
4
6
8
10
12
14
Figure 6: The results of an experiment performed with an image containing a corner feature, given by (17), with σ =1. Left
panels, with (row,column) equal to (1,1) and (2,1): result of Canny’s algorithm. The ground truth lines L
1
and L
2
are shown
in blue in the panel (2,1). Notice that Canny’s edge detector is not centered near the corner point due to the “interference”
between the straight-line edges. Center panels (1,2) and (2,2): the SE features (the ground truth lines are shown in (2,2)).
Notice that the ground truth lines cover all the SE features except for the two nearest to the corner point. Panel (1,3) shows
the result of applying the operator π, defined in (23), to a pair of SE features near to the corner point. The blue circle indicates
the true position of the corner. Notice that the bottom part of the corner feature is not aligned with the SE edges. Finally,
panel (2,3) shows the edge representation after two iterations of the 0-th order compensation algorithm (32)-(33) applied to
the corner feature in panel (3,1). The bottom segment of the corner feature is now much closer to the ground truth.
Then, the estimate for ϑ given by:
ˆ
ϑ = λ
−1
(˜r
−1
(ϕ
0
)) (26)
satisfies
˜r(λ(
ˆ
ϑ)) = ϕ
0
, (27)
f(H(U;
ˆ
ϑ)) = ϕ
0
(28)
(using (11)). Since f ◦H was assumed to be injective,
it follows that
ˆ
ϑ = ϑ, so that the estimator h given by:
h(I(U)) = λ
−1
(˜r
−1
(f(I(U)))), (29)
is centered for the model function H.
Zero order algorithm By letting µ = λ(
ˆ
ϑ), (26) is
equivalent to the equation
˜r(µ)=ϕ
0
(30)
in the unknown µ. If the map ˜r can be written in the
form (12), then (30) becomes:
µ = ϕ
0
− s(µ), (31)
which has a solution µ ∈ λ(Θ) if ϕ
0
∈ r(Θ).An
initial estimate for µ can be obtained through a pro-
jector π: µ
0
= π(ϕ
0
). This estimate can be plugged
into the right hand side of (31), to yield an updated
value µ
1
= ϕ
0
− s(µ
0
) which, under the 0-th order
approximation that s(µ
0
)  s(µ
1
), satisfies (approx-
imately) Eq. (31). If s(µ
1
) = s(µ
0
) then, in general,
ϕ
0
− s(µ
0
) does not belong to λ(Θ) so that the pro-
jector π needs to be applied again. By iterating this
procedure we get
ˆµ
t
= π(ˆϕ
t
) (32)
ˆϕ
t+1
=ˆϕ
0
− s(ˆµ
t
), (33)
with initialization ˆϕ
0
= ϕ
0
. In the more general case
where ϕ
0
is not in r(Θ) (due to additive noise ν, see
Fig. 1) ϕ
0
must be projected onto r(Θ). This case is
not considered in depth here (see however Section B).
Notice that (32) represents a bottom-up “grouping”
step (compare with (23)) and (33) represents a top-
down feedback correction based on the predicted pa-
rameter displacement s(ˆµ
t
) (which can be precom-
puted and accessed through a lookup table). To em-
VISAPP 2006 - IMAGE ANALYSIS
386

phasize the latter point, note that (33) can be written
also as:
ˆϕ
t+1
=ˆµ
t
+

ˆϕ
0
− ˜r(ˆµ
t
)

, (34)
where ˆϕ
0
− ˜r(ˆµ
t
) is also a feedback correction.
If a fixed point ˆµ of the iterative system (32)-(33)
can be found, then it yields a centered estimate for ϑ,
given by λ
−1
(ˆµ) (see Appendix A).
The results of this algorithm on a particular image
containing a corner feature are shown in Fig. 6.
First order algorithm To solve iteratively equation
(31) with a first order approximation of the distortion
map ˜r, let us calculate its Taylor expansion from ˆµ
t
to
ˆµ
t+1
(we assume that the f
k
are centered):
˜r(ˆµ
t+1
)=˜r(ˆµ
t
)+
˜
R(ˆµ
t
) · (ˆµ
t+1
− ˆµ
t
), (35)
where
˜
R(·) is the derivative matrix of ˜r(·). The equa-
tion ˜r(ˆµ
t+1
)=ϕ
0
, where ϕ
0
k
= f
k
(I(S
k
)), then be-
comes:
˜r(ˆµ
t
)+
˜
R(ˆµ
t
)(ˆµ
t+1
− ˆµ
t
)=ϕ
0
. (36)
From this, by replacing ˆµ
t+1
with ˆϕ
t+1
, we get the
iterative system:
ˆµ
t
= π(ˆϕ
t
) (37)
ˆϕ
t+1
=ˆµ
t
+
˜
R
−1
(ˆµ
t
) ·

ϕ
0
− ˜r(ˆµ
t
)

. (38)
Notice that while the 0-th order corrections (33) for
the k-th fragment depend only on the the parame-
ter displacement s
k
for that fragment, each first-order
correction (38) involves the parameter displacement
of all the fragments, because the matrix
˜
R
−1
is not
block diagonal in general.
5 CONCLUSIONS
Estimation of the parameters of complex features
by means of a model hierarchy, where bottom-up
bootstrapping is coupled with top-down feedback
across adjacent layers, yields better accuracy than
purely bottom-up feedforward methods, and with less
computational requirements than direct optimization
methods that do not utilize intermediate representa-
tions. A method has been described to construct
a model hierarchy by fragmenting complex features
into simpler approximating models and to carry out
parameter estimation by compensating for the asso-
ciated model approximation errors (model discrepan-
cies). When multiple fragments are present, this com-
pensating amounts to correcting the parameter distor-
tions due to the interference between the fragments.
These are some task items to be addressed by future
work: evaluate the method with more complex syn-
thetic images and with real data; compare with other
methods, such as those in (K
¨
othe, 2003; W
¨
urtz and
Lourens, 1997); investigate the effect of random ad-
ditive noise and develop suitable mitigation methods;
use linearization techniques to represent high dimen-
sional distortion maps as linear superpositions of low
dimensional maps, so that the method can be applied
to more complex features (e.g., N -junctions); reduce
memory requirements further by means of more so-
phisticated multidimensional interpolation methods.
ACKNOWLEDGEMENTS
Many thanks to Prof. Sanjoy Mitter for pointing out
the role of feedback and for other useful remarks and
suggestions.
A Correctness of the Algorithm
In order to prove the correctness of the algorithm
given by the iterative system (32)-(33), the following
definition is needed. Fix µ
0
∈ λ(Θ) and consider a
displacement δ ∈ Φ from the point µ
0
∈ λ(Θ) to
µ
0
+ δ ∈ Φ. A displacement δ is said to be in the null
set of π at µ
0
, denoted δ ∈N(µ
0
),ifπ(µ
0
+δ)=µ
0
.
We say that the pair (π, f) discriminates the feature
model H if the displacement between the responses
of f to a pair of H-features with local coordinates
µ
0
,µ
1
is never in the null set of π at µ
0
, that is, if for
any µ
0
,µ
1
∈ λ(Θ):
µ
0
= µ
1
⇒ ˜r(µ
1
) − ˜r(µ
0
) ∈N(µ
0
).
Proposition. If f
k
is centered for all k =
1,...,K; (π, f) discriminates the feature model H;
and the system (32)-(33) always converges, then the
resulting estimator is centered for the feature model
H.
Proof. We can assume:
I(S
k
)=H(S
k
; ϑ),
for some ϑ ∈ Θ, so that
ˆϕ
0
k
= f
k
(H(S
k
; ϑ)) = ˜r
k
(µ), (39)
where µ = λ(ϑ). First, let us show that µ is a fixed
point, that is, ˆϕ
t
=ˆϕ
t+1
=ˆµ
t
= µ satisfies both
(32) and (33). (32) is clearly satisfied because π is a
projector on λ(Φ) (see (22)). As for (33), we need to
show that the right hand side is equal to µ. Indeed, by
using (12) and (39) we have:
ˆϕ
0
k
− s
k
(µ)=˜r
k
(µ) − ˜r
k
(µ)+µ
k
= µ
k
.
Now, let us show that µ is the only fixed point. If ˆµ
is a fixed point then, for some ˆϕ ∈ Φ,
ˆµ = π(ˆϕ) (40)
ˆϕ =˜r(µ) − ˜r(ˆµ)+ˆµ. (41)
HIERARCHICAL ESTIMATION OF IMAGE FEATURES WITH COMPENSATION OF MODEL APPROXIMATION
ERRORS
387

From (40) we have that ˆϕ − ˆµ is a null displacement
for π at ˆµ: ˆϕ − ˆµ ∈N(ˆµ); combining this with (41):
˜r(µ) − ˜r(ˆµ)= ˆϕ − ˆµ ∈N(ˆµ). Since (π, f) discrim-
inates the feature model H, this implies ˆµ = µ.
B Mitigation of Additive iid Noise
If the image contains an H-feature instance corrupted
by unstructured noise, that is,
I(U)=H(U; ϑ)+ν (42)
where ν represents a block of identically indepen-
dently distributed random variables, then the estima-
tors f
k
, when applied to the input image I, yield the
intermediate feature ϕ ∈ Φ given by:
ϕ = f (I(U)) = f(H(U; ϑ)+ν)=r(ϑ)+η, (43)
where η is a random variable. If f can be linearized:
ϕ  f (H(ϑ)) + ∇f (H(ϑ)) · ν, (44)
where, for notational simplicity, we let f (H(ϑ)) ≡
f(H(U; ϑ)), then the covariance of ϕ, conditional on
the image containing an H-feature with model para-
meter ϑ, is:
Σ
Φ
(ϑ)=(∇f(H(ϑ)))

· Σ
iid
·∇f(H(ϑ)), (45)
where Σ
iid
= σ
2
n
1 is the covariance of ν. If an esti-
mate of ϑ is available, denoted
ˆ
ϑ, then ϕ can be pro-
jected to r(Θ) based on the metric Σ
Φ
(ϑ) given by
(45), which amounts to a maximum-likelihood (ML)
filtering of the noise signals ν and η, to yield
ϕ
∗
= π
R|
ˆ
ϑ
(ϕ), (46)
where π
R|ϑ
denotes the projector from Φ to R 
r(Θ) based on the metric Σ
Φ
(ϑ).
REFERENCES
Baker, S., Nayar, S., and Murase, H. (1998). Parametric
feature detection. IJCV, 27:27–50.
Blaszka, T. and Deriche, R. (1994a). A model based method
for characterization and location of curved image fea-
tures. Technical Report 2451, Inria-Sophia.
Blaszka, T. and Deriche, R. (1994b). Recovering and
characterizing image features using an efficient model
based approach. Technical Report 2422, INRIA.
Canny, J. (1986). A computational approach to edge detec-
tion. PAMI, 8:679–698.
Casadei, S. and Mitter, S. K. (1996). A hierarchical ap-
proach to high resolution edge contour reconstruction.
In CVPR, pages 149–153.
Casadei, S. and Mitter, S. K. (1998). Hierarchical image
segmentation – part i: Detection of regular curves in a
vector graph. IJCV, 27(3):71–100.
Casadei, S. and Mitter, S. K. (1999a). Beyond the unique-
ness assumption : ambiguity representation and re-
dundancy elimination in the computation of a cover-
ing sample of salient contour cycles. Computer Vision
and Image Understanding.
Casadei, S. and Mitter, S. K. (1999b). An efficient and prov-
ably correct algorithm for the multiscale estimation of
image contours by means of polygonal lines. IEEE
Trans. Information Theory, 45(3).
Deriche, R. and Blaszka, T. (1993). Recovering and charac-
terizing image features using an efficient model based
approach. In CVPR.
Deriche, R. and Giraudon, G. (1990). Accurate corner de-
tection: An analytical study. ICCV, 90:66–70.
Deriche, R. and Giraudon, G. (1993). A computational
approach for corner and vertex detection. IJCV,
10(2):101–124.
K
¨
othe, U. (2003). Integrated edge and junction detection
with the boundary tensor. In ICCV ’03, page 424.
Marr, D. (1982). Vision. W.H.Freeman & Co.
Nalwa, V. S. and Binford, T. O. (1986). On detecting edges.
PAMI, 8:699–714.
Nayar, S., Baker, S., and Murase, H. (1996). Parametric
feature detection. In CVPR, pages 471–477.
Perona, P. (1995). Deformable kernels for early vision.
PAMI, 17:488–499.
Rohr, K. (1992). Recognizing corners by fitting parametric
models. IJCV, 9(3).
Steger, C. (1998). An unbiased detector of curvilinear struc-
tures. PAMI, 20(2):113–125.
W
¨
urtz, R. P. and Lourens, T. (1997). Corner detection
in color images by multiscale combination of end-
stopped cortical cells. In ICANN ’97: Proceedings of
the 7th International Conference on Artificial Neural
Networks, pages 901–906, London, UK. Springer-
Verlag.
VISAPP 2006 - IMAGE ANALYSIS
388