STRATEGIES FOR FAST TRUE MOTION BLOCK MATCHING

Hendrik van der Heijden, Fabian Wenzel, Rolf-Rainer Grigat

Hamburg University of Technology

Vision Systems, 4-08/1

Harburger Schlossstr. 20

21079 Hamburg, Germany

Keywords:

fast block matching, motion estimation, true motion.

Abstract:

Block matching is a widely used method for fast motion estimation. Although using a very simple motion

model, which does not ﬁt most real world video material, many motion compensating video compression

algorithms use block matching because of its speed. Applications based on true motion vector estimates often

use an optical ﬂow algorithm because of their higher need for accuracy at the expense of increased computing

time. This paper presents a modiﬁed block matching algorithm suitable for true motion applications. A

modiﬁed full search will be used on a cost function consisting of SAD and a vector ﬁeld smoothing term.

Several strategies as search center prediction, spiral search, early search termination and multilevel successive

elimination are implemented to keep the computational demand low. This way, high-quality estimates can be

computed in real-time.

1 INTRODUCTION

Motion Estimation (ME) is the basis for many digital

image processing applications. In video coding, the

objective of a ME algorithm is to minimize the resid-

ual intensity difference after motion compensation.

Mostly block matching ME algorithms are used here

because of speed. Typically, ME through minimiz-

ing intensity differences is not identical to determin-

ing true motion, which is deﬁned as the physical 3D

motion projected onto the image plane. If true motion

estimates are required, ME is usually done by an op-

tical ﬂow (OF) algorithm, which tend to be time con-

suming. This paper adopts a motion smoothness con-

straint, as it is an essential aspect of optical ﬂow algo-

rithms, to be used in block matching. As search space

subsampling algorithms like three step search are not

suitable for true motion estimation, an adapted full

search is used. Several techniques are implemented

to keep computational demands low on today’s desk-

top PCs. While the resulting motion ﬁeld still has

block resolution, correctness of estimates may im-

prove from this added constraint, making it useful

for some applications which otherwise would need a

computational intensive optical ﬂow approach.

2 BLOCK MATCHING

Block matching algorithms calculate a motion vector

ﬁeld, which consists of one vector for each block in

the current frame pointing to its correspondence in a

reference frame. The current frame I

is divided into

non-overlapping square blocks of size B × B, typi-

cally 16 × 16 pixels. For each block B

i,j

at position

(x, y) a corresponding block of the same size at posi-

tion (x + v

,y + v

) in the reference image I

t+1

determined by solving the following equation:

v =(v

) = argmin

)∈S

(x,y )

) (1)

Hence, a matching error C

(x,y )

is minimized over

a set S of search positions. The resulting displace-

ment vector v is assumed to represent the motion of

the block. Typically, a cost function like the sum of

absolute differences (SAD) is chosen.

SAD

(x,y )

B−1



j=0

B−1



i=0

(x + i, y + j) − I

t+1

(x + v

+ i, y + v

+ j)|

(2)

359

van der Heijden H., Wenzel F. and Grigat R. (2006).

STRATEGIES FOR FAST TRUE MOTION BLOCK MATCHING.

In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 359-363

DOI: 10.5220/0001368503590363

 SciTePress

2.1 Construction of the Search Space

The search space S is a set of discrete search positions

with integer coordinates, as the SAD function deﬁnes

no ﬁner resolution. A full search deﬁnes S as the set

containing every position within a rectangle with size

2sw +1(sw: search window size).

S = {(v

)|−sw ≤ v

≤ sw} (3)

Other algorithms like Three Step Search (Wang and

Mersereau, 1999) or 2D Logarithmic Search (Jain and

Jain, 1981) reduce the number of initial search posi-

tions to 9 resp. 5 and add more positions near the min-

imum position in several steps. As, due to their con-

struction, a best match is not guaranteed to be found,

only full search is used in the following.

Solving (1) is done by evaluating the SAD for

every position in S. The SAD calculation can be

aborted early, if the partial SAD already is above the

lowest SAD found so far.

Further speedup is possible by reducing the number

of search positions (early abort of search), the com-

plexity of SAD calculation (using estimates for the

SAD) and optimizing the visiting order of the search

positions. All of these possibilities are used in this

work and described in the following sections.

2.2 Multilevel Successive

Elimination Algorithm

The Multilevel Successive Elimination Algorithm

(MSEA) (Gao, 2003) speeds up SAD calculation.

It deﬁnes several lower bounds SAD

on the SAD

with decreasing quality and computational demands

to speed up SAD calculation.

Consider P

as the set of all pixel positions in

a block. P

l,i

is the level-l quad-tree partition i of

, it contains all pixels of sub-block i with size

. Vectors a and b contain all pixels of the

two blocks to be compared. The evaluation of a new

search position consists of subsequently computing

SAD

, SAD

L−1

... SAD

, and is aborted as soon

as SAD

>SAD

∗

, SAD

∗

being the lowest SAD

found so far.

SAD ≤ SAD



0≤j≤l





i∈P

l,j

−



i∈P

l,j



(4)

The sums over block partitions are precalculated

for every position in the reference image I

t+1

and

every level, taking additional memory of 2(L +1)

times the size of a single input image. Precalculation

time for B=16 and 2 levels equals that of 4.5 SAD

calculations per block. In this case, most positions

with sub-optimal SAD values can be eliminated with

of the operations a regular SAD would take.

2.3 Prediction and Search Position

Order

It can be seen in section 2.2 that MSEA performes

well if a good search position is known as early as

possible. This fact can be utilized as neighboring

blocks tend to have highly correlated motion vectors

(MVs). In our approach MVs of three adjacent blocks

(left, top and top-right, which have already been com-

puted), three temporally adjacent block MV (same

block, bottom-left and bottom-right in the previous

motion ﬁeld) and the zero motion MV are evaluated

ﬁrst. This choice of neighbors is taken from (Tourapis

et al., 2001) and extended by the two diagonal tempo-

ral candidates from (de Haan et al., 1993) to allow

better prediction of upward motion.

The MV having the lowest SAD deﬁnes the search

center. As this prediction most of the time leads to the

global minimum SAD being near the search center,

the remaining positions of S are visited in expanding

spiral order starting from the search center. The ef-

fective size of the search window will be larger than

that of a static search center, because the search win-

dow size now limits the maximum detectable accel-

eration instead of the maximum speed. The search is

aborted, if n rings have been completed without ﬁnd-

ing a lower cost position. n can be adjusted to favor

speed or quality of the algorithm. In the following

experiments n =3is used.

2.4 Modiﬁcation Towards True

Motion

Optical ﬂow algorithms often incorporate a motion

ﬁeld smoothness constraint so that local variations in-

crease cost (Brox et al., 2004). Equations determining

MVs usually include image intensities of just a few

pixels directly, which barely is a sound measure of im-

age part similarity, even in strongly textured regions.

Constraining adjacent MVs to be similar adds indi-

rect inﬂuence of more pixels, expanding the effective

image area used for similarity measurement, which

lowers noise sensitivity. As a second effect, uniform

image regions adopt MVs of surrounding textured re-

gions.

While block matching directly includes enough

pixels for textured regions, the SAD measure is not

meaningful in poorly textured regions, regions with

non-zero gradient in only one direction or when cal-

culated on periodic image content. In this cases, tak-

ing adjacent MVs into account may improve correct-

ness of determined motion vectors. In our work, we

combine the SAD with an additive term increasing

with MV distance from its surrounding MVs, leading

to a modiﬁed cost function (5).

VISAPP 2006 - MOTION, TRACKING AND STEREO VISION

360

C(u, v)=SAD(u, v)+dB

f(min

(u, v) − N

)

(5)

f(x)=



if x ≤ 1

x else

(6)

are the left, top and top-right neighbor block

MVs, the distance to the nearest MV is embedded in

a function f which reduces damping for small (sub-

pixel) deviations. As only the distance to the nearest

MV is considered, the damping term penalizes posi-

tions which do not have at least one similar neighbor

MV. A neighbour MV reliability based weighting of

inﬂuence would be preferable, but was not considered

here. Damping factor d can be adjusted to the proper-

ties of the input images. In our experiments d =0.5

is a good value for most cases with B =16.

2.5 Subpixel Resolution

After determining the best matching pixel position for

a block, a second search is done around this location

reﬁning the MV to subpixel resolution. A 2D loga-

rithmic search with an initial search distance of 1/2

pixel evaluates the cost function on the current block

and a linearly interpolated block from the reference

image. MSEA is only applicable at full-pixel posi-

tions, so subpixel reﬁnement can take more time than

all other ME components together.

2.6 Motion Field Upsampling

In order to provide motion vectors for every pixel

in an image, the block-based vector ﬁeld is upsam-

pled with one of three algorithms: constant and lin-

ear interpolation as well as hierarchical block ero-

sion(de Haan et al., 1993). The latter divides each

block in four sub-blocks and assigns the vector me-

dian of its parents vector and the vectors of its two

directly adjacent blocks of parent size to each sub-

block. This ﬁlter is applied iteratively down to sub-

blocks of size 2 ×2 pixels, then constant interpolation

is applied to save time.

3 EVALUATION

We evaluated our proposed algorithm with respect to

computing time (on an Athlon64 3000+) and accu-

racy. In order to evaluate the true error, the synthetic

yosemite sequence (Quam, 1984) with known cor-

rect motion ﬁeld (ground truth) has been used. A

simple 3 × 3 smoothing ﬁlter kernel is applied to

decrease aliasing effects. Figure 1 shows a sample

frame, ground truth and motion estimates.

(a) Frame 2 (b) Ground truth

polation, B=16

(d) estimate, block ero-

sion, B=8

Figure 1: Yosemite sequence, velocity ﬁelds of correct mo-

tion (ground truth) and two estimates.

Table 1: AAE improvement when using our smoothness

constraint. For d =0, our cost function degrades to stan-

dard SAD. Other parameters are B =16, sw =16,

1/32 pixel MV resolution, linear interpolation. Computa-

tion times are given for the whole sequence.

Sequence d AAE time

Yosemite with 0 3.84

◦

± 6.91

◦

399ms

black sky

0.71 3.43

◦

± 5.71

◦

389ms

Yosemite with 0 2.80

◦

± 3.72

◦

328ms

sky cropped

0.5 2.52

◦

± 2.19

◦

351ms

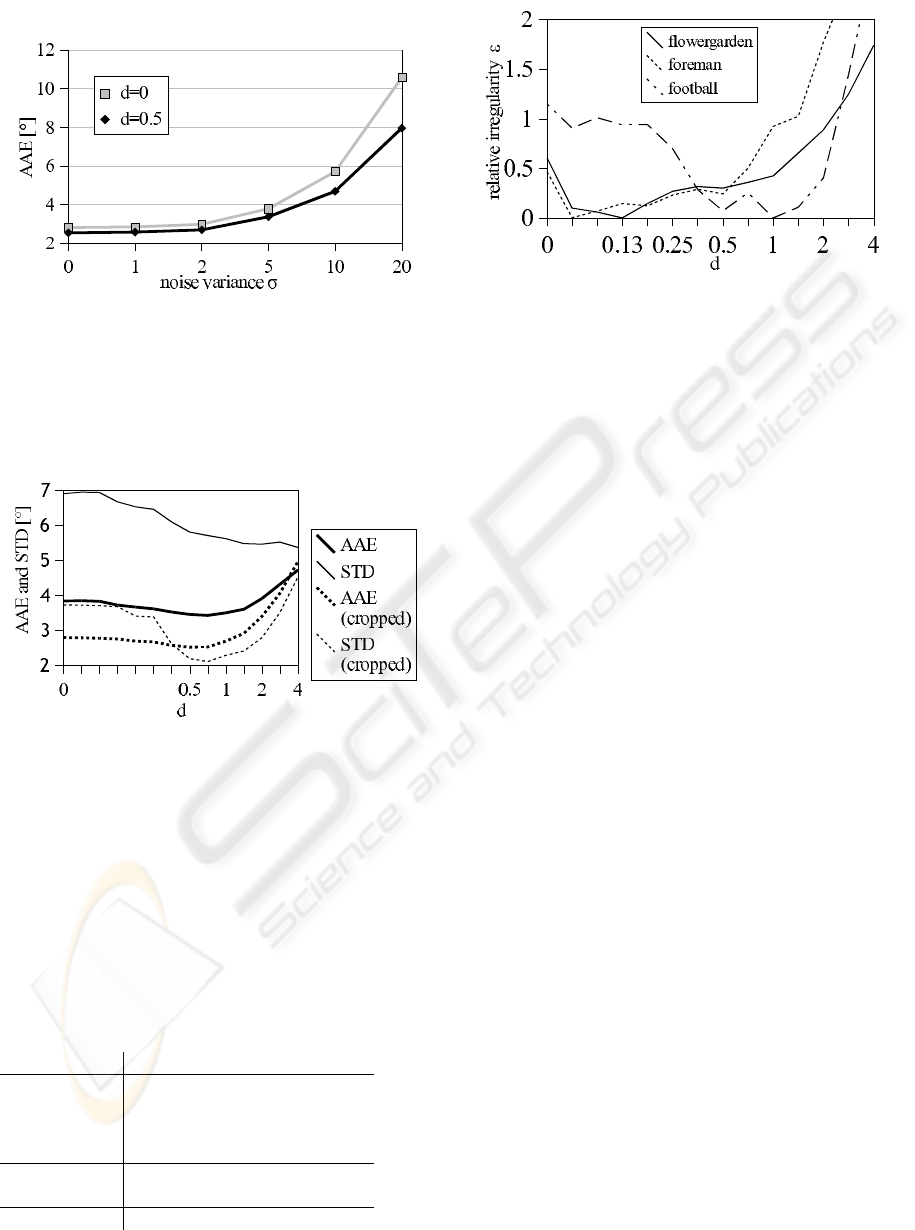
Figure 3 displays the average angular error (Horn

and Schunck, 1981) and its standard deviation at dif-

ferent damping factors. As the boundary between sky

and land cannot be modeled adequately with blocks,

a second measurement is taken with the top 72 pixel

lines cropped. Results of these tests in table 3.1 show

slight improvements of angular error and standard de-

viation when using our motion ﬁeld smoothness con-

straint. While computation gets a bit faster due to

the large black area in the ﬁrst test, our extension in-

creases computation time by 7% in the second test.

3.1 Noise Sensitivity

To evaluate noise sensitivity in textured regions,

we added gaussian noise with variance σ ∈

[0, 1, 2, 5, 10, 20] to the Yosemite sequence with

cropped sky and measured the AAE with and with-

out our damping extension. Results in ﬁgure 2 shows

some improvement in noisy cases.

STRATEGIES FOR FAST TRUE MOTION BLOCK MATCHING

361

(a) Frame 2

Figure 2: Noise sensitivity, average angular error of motion

estimates on Yosemite sequence (sky cropped) with added

gaussian noise.

Figure 3: Yosemite sequence, average angular error (AAE)

and standard deviation (STD) of full image with black sky

and with sky cropped at different damping factors, B=16,

upsampling via linear interpolation. Minimum values are

3.43 ± 5.71 (full) resp. 2.53 ± 2.11 (cropped).

Table 2: Yosemite sequence, linear interpolation, B =16,

sw =16, d =0.71 (optimal). For a block size of B =8

two additional results are given. For comparison, a good

100% density 2D OF result (Farneb

ack, 2000) is listed, its

computing time is 16s per frame on a 360MHz Sun Ultra

60.

resolution AAE time/frame

1 pixel 8.94

◦

± 8.94

◦

11.9ms

1/2

5.02

◦

± 6.08

◦

14.7ms

1/8

3.55

◦

± 5.73

◦

23.0ms

1/32

3.43

◦

± 5.71

◦

32.6ms

1 (BS=8) 9.10

◦

± 9.35

◦

24.9ms

1/32 (BS=8)

3.54

◦

± 5.31

◦

53.7ms

OF 1.40

◦

± 2.57

◦

see caption

Figure 4: Relative irregularity at different damping factors,

minimum set to zero, block erosion, B=16.

3.2 Real World Sequences

In a second experiment, real world sequences with un-

known ground truth, a motion ﬁeld irregularity mea-

sure ε (7) is used, which is deﬁned as the average an-

gular error (AAE) between a forward ME to the next

image and a backward ME to the previous image.

ε(I

)=AAE(−BM(I

t+1

),BM(I

t−1

)) (7)

This measure yields low values when computed

correspondences are stable. False correspondences

result in motion vectors jumping from one frame to

another, i.e. in large values of . Experiments with

various parameters on several synthetic image se-

quences indicate an approximately linear connection

between ε and ground truth AAE.

Figure 4 shows the irregularity of three stan-

dard sequences, ﬂowergarden (uniform fore-

gound/background motion), foreman (ﬁrst 70 frames

only, medium motion) and football (fast, turbulent

motion).

3.3 Computation Time

Table 3 gives computation times for three standard se-

quences for pixel resolution and the additional time

per subpixel bit, which has shown to be nearly con-

stant independent of subpixel resolution, for block

sizes B =8and B =16. The impact of MSEA

on computation time was also measured in a short ex-

periment. While a spiral full search speeds up by a

factor of two, our described search algorithm gains

only about 10% speed for d =0and loses up to 4%

with d =0.5 in the ﬂowergarden sequence. In the lat-

ter case, the overhead introduced by MSEA is larger

than the time it saves. MSEA gives best speedup on

sequences with poor motion predictabiliy, which usu-

ally are one taking the most time.

VISAPP 2006 - MOTION, TRACKING AND STEREO VISION

362

Table 3: Computing times per frame for three sequences

(block erosion, sw=16, d=0.5).

block sequence time for additional time

size

pixel res. per subpixel bit

ﬂowergarden 29.1ms 7.6ms

foreman 31.3ms 8.3ms

football 33.1ms 8.3ms

ﬂowergarden 14.4ms 5.5ms

foreman 16.6ms 6.6ms

football 19.8ms 6.7ms

As can be calculated from table table 3, CIF

(352x288) sized image sequences can be processed

in real time (25Hz, below 40ms per frame) with 1/8

pixel resolution, even when containing turbulent mo-

tion like in the football sequence. As processing time

is data dependent, subpixel resolution or the early ter-

mination criterion can be adaptively adjusted to meet

real time requirements for every frame. Only one vec-

tor per block is computed, so our results have lower

resolution than optical ﬂow estimates. On compara-

ble hardware, a recent OF implementation (Bruhn and

Weickert, 2005) takes about 150ms per 160x120 pixel

frame.

4 CONCLUSION

We presented strategies for fast true motion block

matching. Our damping extension improves block

matching results towards optical ﬂow estimation and

reduces noise sensibility. Block erosion upscaling

of motion estimates to pixel resolution removes vis-

ible block structure. Prediction and MSEA have been

adopted to keep computational demands low enough

for real time processing. As motion discontinuities

are rather badly modeled by the block structure used,

there is a desire for better edge treatment. This can

be done in several ways, for example weighting the

SAD cost with a windowing function and ﬁnding cor-

respondences for overlapping blocks as in the exper-

imental BBC Dirac video codec. Another approach

would be recognizing blocks containing more than

one motion domain and determining a decomposi-

tion of block content and motion vectors with mini-

mal SAD for each part (Orchard, 1993).

REFERENCES

Brox, T., Bruhn, A., Papenberg, N., and Weickert, J. (2004).

High accuracy optical ﬂow estimation based on a the-

ory for warping. In Proceedings of the 8th European

Conference on Computer Vision.

Bruhn, A. and Weickert, J. (2005). Towards ultimate motion

estimation: Combining highest accuracy with real-

time performance. To appear in Proc. 10th Interna-

tional Conference on Computer Vision (ICCV 2005).

de Haan, G., Biezen, P., Huijgen, H., and Ojo, O.

(1993). True-motion estimation with 3d recursive

search block matching. IEEE Trans. on Circuits and

Systems for Video Tech., 3(5).

Farneb

ack, G. (2000). Fast and accurate motion estima-

tion using orientation tensors and parametric motion

models. In Proceedings of 15th IAPR International

Conference on Pattern Recognition, September 2000.

Gao, Duanmu, Z. (2003). A multilevel successive elimina-

tion algorithm for block matching motion estimation.

IEEE Trans. on Image Processing, 9(3).

Horn, B. and Schunck, B. (1981). Determining optical ﬂow.

Artiﬁcial Intelligence, 17(1-3):185–203.

Jain, J. and Jain, A. (1981). Displacement measurement

and its application in interframe image coding. IEEE

Trans. Commun., COM-29:1799–1808.

Orchard, M. (1993). Predictive motion-ﬁeld segmentation

for image sequence coding. IEEE Trans. on Circuits

and Systems for Video Tech., 3:54–70.

Quam, L. (1984). Yosemite image sequence.

Tourapis, A. M., Au, O. C., and Liou, M. L. (2001). Pre-

dictive motion vector ﬁeld adaptive search technique

(PMVFAST) - enhancing block based motion estima-

tion. In Proceedings of Visual Communications and

Image Processing 2001 (VCIP’01).

Wang, H. and Mersereau, R. (1999). Fast algorithms for the

estimation of motion vectors. IEEE Transactions on

Image Processing, 8(3).

STRATEGIES FOR FAST TRUE MOTION BLOCK MATCHING

363