
COGNITIVE VISION AND PECEPTUAL GROUPING BY
PRODUCTION SYSTEMS WITH BLACKBOARD CONTROL:
An example for high-resolution SAR-images
Eckart Michaelsen, Wolfgang Middelmann
FGAN-FOM, Gutleuthausstrasse 1, 76275 Ettlingen, Germany
Uwe Sörgel
Institute of Photogrammetry and GeoInformation, University of Hanover, Nienburger Satrasse 1, 30167 Hannover,
Germany
Keywords: Cognitive vision, Perceptual grouping, Production systems, Blackboard control, SAR images.
Abstract: The laws of gestalt-perception play an important role in human vision. Psychological studies identified
similarity, good continuation, proximity and symmetry as important inter-object relations that distinguish
perceptive gestalts from arbitrary sets of clutter objects. Particularly, symmetry and continuation possess a
high potential in detection, identification, and reconstruction of man-made objects. This contribution
focuses on coding this principle in a full automatic production system. Such systems capture declarative
knowledge. The procedural details are defined as control strategy for an interpreter. Often an exact solution
is not feasible while approximately correct interpretations of the data with the production system are
sufficient. Given input data and a given production system the control acts accumulative instead of
reducing. The approach is assessment driven features any-time capability and fits well into the recently
discussed paradigms of cognitive vision. An example from the automatic extraction of groupings and
symmetry in man-made structure from high resolution SAR-image data is given. The contribution also
discusses the relations of such endeavour to the “mid-level” of what is today proposed as “cognitive vision”.
1 INTRODUCTION
A human subject can recognize and distinguish
important gestalts even from pictorial data that he or
she is not familiar with. Looking e.g. at the very
high-resolution SAR-image displayed in Fig. 1
everyone will almost immediately perceive the
important building features although only a minority
of people is aware of the special properties of this
kind of imagery. Yet SAR-experts have little success
trying to code automatic building detection from
such data. Partly, this results from the sheer size of
these images – this one has decimetre resolution
with an area of several hundred meters covered –
partly from the particular nature of noise in
RADAR-data (Klausing & Holpp 2000). The
important building features that humans perceive are
of non-local nature; they disappear when only a
small window of say 49x49 pixels is shown (such as
is done in the lower part of Fig.1). Recall that most
iconic operations operate on much smaller window
sizes such as 7x7 pixels or even less. One may well
argue that before processing these data should be
scaled down. However, the antenna construction and
the SAR-processing may well resolve fine structures
of this size (Ender & Brenner 2003) and we should
not throw away possibly important information that
has been measured.
Numerous machine vision contributions rely on
scale pyramid processing instead (e.g. Laptev et al.
2000). This repeats the methods on several scale
levels of the image usually obtained by downscaling
with factor 2 at each level. However, a line structure
in these data may appear at a very fine scale –
broken by gaps and yielding only small line
segments at this scale, while it may disappear in
noise in coarser scale completely. A considerable
alternative is the large variety of Hough transform
methods (Leavers 1993).
109
Michaelsen E., Middelmann W. and Sörgel U. (2006).
COGNITIVE VISION AND PECEPTUAL GROUPING BY PRODUCTION SYSTEMS WITH BLACKBOARD CONTROL: - An example for high-resolution
SAR-images.
In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 109-115
DOI: 10.5220/0001368101090115
Copyright
c
SciTePress

Figure 1: X-band SAR image with a building and small
section from it.
Being aware of the trouble that automatic
systems have, we find that humans perform
remarkably well. We emphasize that this holds for
almost any kind of noisy high resolution pictorial
data also including those from many kinds of e.g.
medical sensors. In the literature this striking
capabilities of human observers are known as the
“gestalt perception” borrowing the word “Gestalt”
from German language. It is now almost a hundred
years that this topic is being studied. Psychological
investigations identified the relations similarity,
good continuation, proximity and symmetry as
important inter-object relations that distinguish
perceptive gestalts from arbitrary sets of clutter
objects almost hundred years ago (Wertheimer
1927). Of these only proximity is of local nature.
Research in incorporating perceptive capabilities
based on these relations into machine vision also has
a quite remarkable history (Marr 1982, Lowe 1985)
There is joint work from psychologists, artificial-life
researchers, neurophysiologists, Darwinists and
computer vision experts to derive these principles
from co-occurrence statistics of natural images and
the principles of evolution of species (Guo et al.
2003). Yet much of the latest work on perceptive
grouping concentrates on the implementation of
local gap-filling techniques like tensor voting
(Medioni et al. 2000).
This contribution focuses on automatically
identifying symmetry and repetitive structure by a
production system. To this end a multistage
assessment driven process is set up. The first stage
described in section 2 transforms the iconic image
information into sets of structural objects like spots
and short line segments. These primitive objects are
combined to scatters, long lines, salient rows, and
angles taking the laws of gestalt-perception into
account, see section 3. The last stage of the
production system consists of identifying and
assessing the symmetry of angle pairs. Section 4
describes the methodology for efficient processing
the production system. As result strong hypotheses
of symmetry axes and scatterer rows are determined
in section 5. Throughout the paper we discuss the
relation to what is recently being discussed as
“cognitive vision”. This is particularly emphasized
in the concluding section 6.
2 TRANSFORMING ICONIC
INFORMATION TO SETS OF
STRUCTURAL OBJECTS
The image neighbourhood is closely connected to
just one relation (proximity) among many others that
interest us. Large image regions may contain
nothing of interest just homogenous returns with
some noise multiplied to it. Therefore the image
matrix is not an appropriate representation. Instead
we use sets of objects that are extracted from the
image by feature extraction methods. Fig. 2 shows a
set of spot pixel objects P with 7173 elements and
Fig. 3 shows a set of short line objects L with 4404
elements. In comparison to the 2400x2300 grey
value pixels of the original image this is a significant
reduction, while the major building features remain
in this representation..
VISAPP 2006 - IMAGE UNDERSTANDING
110

Figure 2: Set of primitive objects spot pixel – P.
Figure 3: Set of primitive objects line – L.
Objects P are constructed using a spot-filter
(Michaelsen et al. 2002) on a reduced version of the
image by factor 4. The procedure has two
parameters a window radius (set to 8 pixels) and a
decision threshold (set to 10%) which is a factor of
the maximal value found by the filter in the present
image section. They are labelled with subpixel-
accurate x- and y-coordinate and the strength above
threshold. The latter gives their assessment. It is
visualised as grey-value in Fig. 2. White means that
there is no object P in that location. Each object P
states evidence for a bright spot in that position.
Objects L are constructed using the squared
averaged gradient filter (Foerstner 1994) on versions
of the image reduced by factors 2, 4, 8 and 16. This
filter gives a symmetric 2x2 matrix for each image
position. Matrices with a big eigenvalue and a small
one indicate evidence for an edge or for a line at the
associated position. For the filter there is a radius σ
(set to 1 pixel here). It makes sense to prolong these
very short line segments in each scale version of the
image separately before joining the whole set for
subsequent processing. This is done by running a
trivial system containing only the production P
2
described in the next section for a fixed number of
cycles. Thus the basis objects for structural analysis
are computed.
The resulting set of primitive objects may be
significantly improved (i.e. contain less noise but the
same information) if sophisticated a iconic filter
operation precedes the extraction process
(Michaelsen et al. 2005). For simplicity we have
omitted this step for this work
3 CODING COGNITIVE VISION
AND GESTALT RELATIONS IN
PRODUCTIONS
Gestalt psychology teaches certain geometric
relations as the key to perception. A set of parts
fulfilling these constraints forms a whole that is
described more briefly and distinctively. A straight
forward way to code this for machines is to use
production rules (or short productions). Such
productions have occasionally been used for remote
sensing and computer vision (Draper et al., 1989,
Stilla et al. 1996). Main benefits from the use of
production systems are modularity of knowledge
and clear separation of the declarative knowledge –
i.e. the productions - from the procedural decisions –
i.e. the control. Each production P consists of an
input side Σ, a constraint relation π, an output side
Λ, and a function φ. The set of productions used for
a given task is called production system. Compared
to rule-based systems discussed in the AI and vision
community long time ago (e.g. Matsuyama and
Hwang, 1990) the system presented here contains
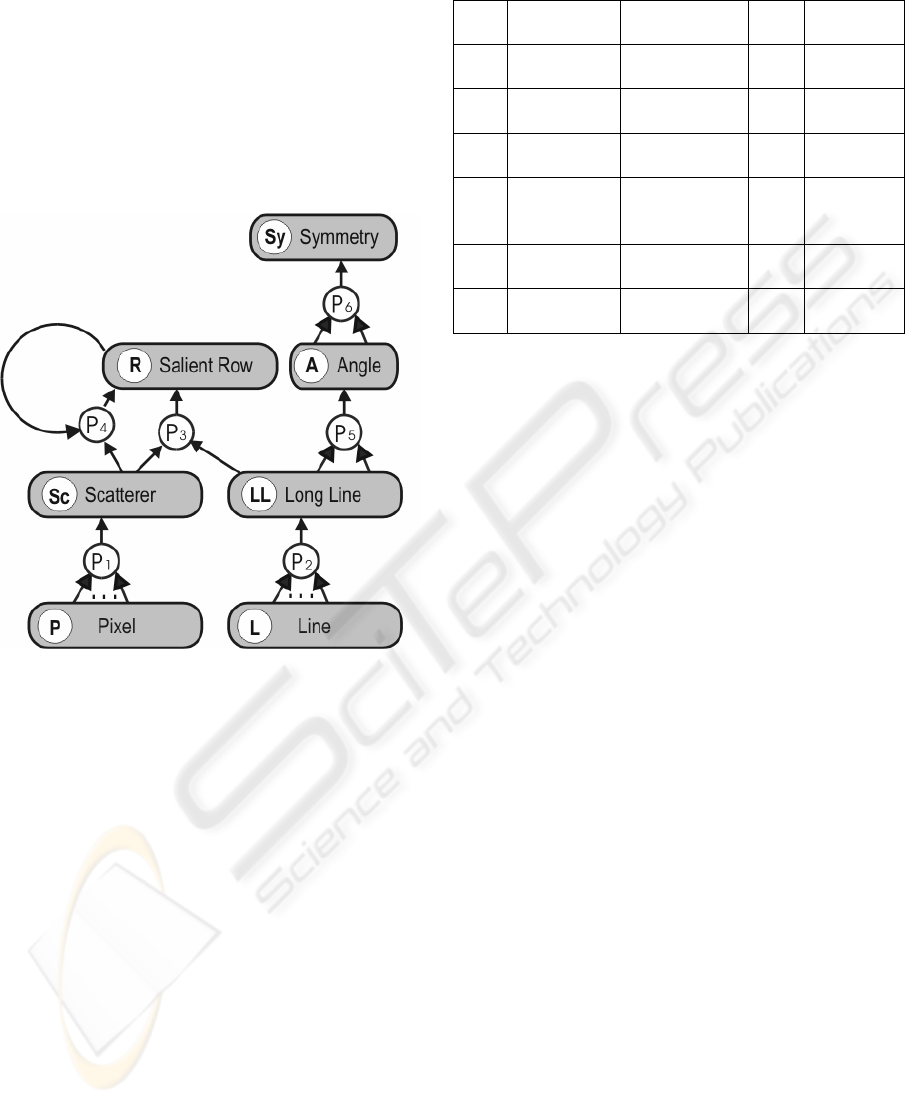
only few productions. In Fig. 4 it is presented as
production net. Circular nodes represent the
productions while elongated nodes represent object
concepts. Object names are short symbols, so there
is one or two words with each object node to explain
what kind of object it is.
The output side Λ most often only consists of a
single symbol whereas the input side Σ may consist
of a fixed tuple (P
3,…,6
) or a set of objects (P
1,2
) of
the same type. Of most interest are productions P
4
COGNITIVE VISION AND PECEPTUAL GROUPING BY PRODUCTION SYSTEMS WITH BLACKBOARD
CONTROL - An example for high-resolution SAR-image
111
and P
6
. P
4
consecutively adds one scatterer object
Sc after the other to row objects R. This recursive
process is initialised using the direction of a
neighbouring long line object LL. P6 constructs
symmetry axis from pairs of angle objects A. This
alone is a non-local constraint and thus may cause
excessive computational effort. For building
detection we can further restrict one leg of one angle
object A to be collinear with the other leg of the
other angle object A. This makes the search more
robust.
Figure 4: Production-net visualisation.
The cognitive vision paradigm – as it has been
formulated in the research roadmap (ECVision,
2005) emphasize automatic acquiring of such
knowledge from large corpi of data. However, for
many tasks – such as working towards automatic
vision for SAR-sensors of the next generation –
there are only some few sample images available.
There also is no need to (machine-) learn the
principles of perceptual grouping from large samples
of data. They are known from nearly hundred years
of psychological research. There is probably a
potential for fostering robustness through adaptation
of the thresholds and parameters inherent in the
constraint relations π. We have proposed statistical
calculus for this with models for background and
target structure (Michaelsen & Stilla 2002). This
needs a far bigger data corpus than is available now,
and it requires tremendous human labour for the
labelling of a learn set – and a test set for
verification.
Table 1: Productions listed as table.
4 THE ACCUMULATIVE
CONTROL A PARADIGM FOR
COGNITIVE PECEPTION
The objective for the control of the production
system is to handle robustly many thousand objects.
Two possibilities for the control are discussed here.
Reduction: Standard interpretation of
production systems following e.g. Matsuyama and
Hwang (1990) works reductively: Given a set of
productions and a set of data the productions are
performed serially. For a system like the one
presented above the interpreter would select a
production and a subset that symbolically fits into
the input side (e.g. a pair of objects (LL, LL) for P
5
)
test the constraint relation (in the example proximity)
and carry out the production in case of success.
Reduction means that the original object pair is
removed and replaced by the new object A. Since
selection of pairs is of quadratic computational
complexity it is good advice to have one element of
the input side triggering a search for partners that
fulfil the constraint without listing all objects that
are far away. We call such a pair of an object and a
production to be tested with it a “working element”.
The main problem with this reduction technique is
the administration of the control. It has to keep track
of every step it took. Recall that there may be
alternative possibilities for the selection step. The
control may have to “undo” a sequence of steps and
then try again with other selections. Thus the
computational complexity of the search is bounded
by no less than O(2
n
) where n is the maximal serial
Σ
π
Λ φ
P
1
{P,…,P} proximity Sc mean
P
2
{L,…,L} colinearity LL regres-
sion
P
3
(SC,LL) proximity R copy
P
4
(SC,R) good
continuation
∧ similarity
R mean
P
5
(LL,LL) proximity A intersect
P
6
(A,A) symmetry
∧ colinearity
Sy mid axis
VISAPP 2006 - IMAGE UNDERSTANDING
112
depth of the search. If the production net contains
cycles (like the one presented above) the serial depth
will only be bounded by the number of objects (each
reduction removes at least one object). Such control
may be semantically correct but it will not be very
robust concerning the computational effort
dependence on the data. Particularly for recognition
from image data it is necessary to trade the 100%
semantic correctness for more robustness in the
control. However, these approaches are still being
pursued today e.g. using PROLOG (Cohn et al.
2003). Of particular interest today for the cognitive
vision issue is the logical structure best suited for
vision tasks. The question is raised whether one
should utilize deductive, inductive or even abductive
logics. All of these attempts scale badly with rising
number of data instances.
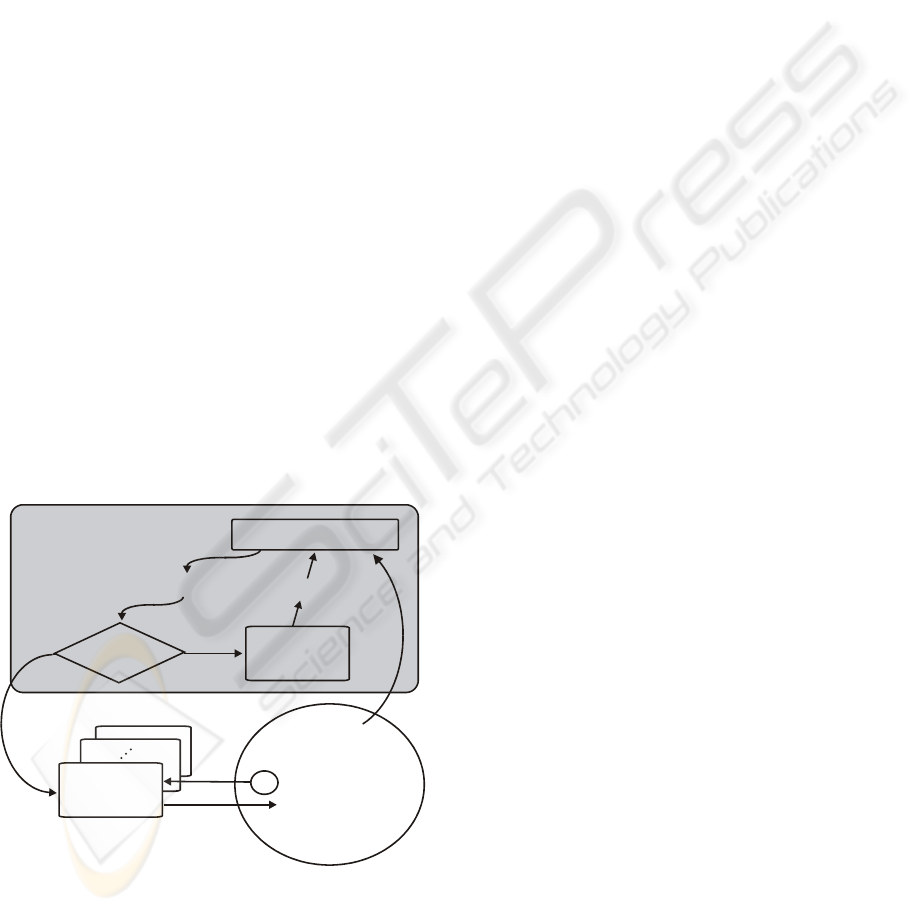
The Accumulating Interpretation Cycle: This
follows the well known AI-paradigm of blackboard
architecture. Given a production system P ={S, A,
P} a working element is defined as quadruple e=(s, i,
as, pm) where s is a symbol from S, i is an object
instance index, as is an assessment and pm is a
production module index. Assessments are taken
from the continuous ordered interval [0, 1]. A
production module is always triggered by a
particular object instance. It contains code that
queries the database for partner instances which
fulfil the constraint relation π of the production
given the triggering object instance.
e
pm=nil
?
sorted queue
yes
connectivity
of prod.-net
{e,...,e}
no
set of
accumulated
objects
production
module
dispatcher
Figure 5: The accumulative interpretation cycle.
Usually search regions are constructed (e.g. a
long stripe shaped region with the triggering Line
instance in the centre for P
2
). If the query results in a
non-empty set the module will create new instances
according to the functional part φ of the production.
Some productions need more than one module (e.g.
p4 may be triggered by a Row instance or by a Spot
instance requiring different queries). The set of
module indices is expanded by nil. Always when a
new object instance is created – either by an external
feature-extraction process or by one of the
production modules – also a corresponding new
working element is added using this module index
nil (meaning that there is no module assigned yet).
The set of working elements is called the queue. It is
sorted occasionally (e.g. every 100 interpretation
cycles) with respect to the assessments. The central
control unit (AI-people call it dispatcher) always
picks working elements from the queue. If the
module index of an element is nil it will be replaced
by new working elements with appropriate module
indices (recall that each connection from a symbol to
a production in the production-net corresponds to a
production module, i.e. a possibility to be tested). If
there is a non-nil module index attached the
dispatcher will trigger the indicated module by the
corresponding object instances. The whole
interpretation cycle is indicated in Fig. 5.
Modules may be run in parallel on different
processors. The dispatcher can start picking
elements from the queue the moment the first
primitive instances are inserted. It terminates
inevitably when the queue happens to run empty.
But usually it will be terminated before, either by
external processes or the user, or by limiting the
number of cycles or time. Obviously the
accumulative control features any-time capability.
The advantages of the accumulating interpretation
cycle have been originally described in the context
of syntactic pattern recognition by Michaelsen
(1998a, 1998b)
There is good evidence that a large portion of the
remarkable visual capabilities of man is due to the
visual motor system and its elaborated control. For
the SAR-application we do not need to move
physical sensors during recognition. The data
provide high resolution everywhere and our control
shifts the focus of attention around freely, because
the data are organized as sets. The eye saccade
control of a human observer is replaced by the
assessment driven control of our blackboard. This
stresses the importance of further research on the
assessment functions.
COGNITIVE VISION AND PECEPTUAL GROUPING BY PRODUCTION SYSTEMS WITH BLACKBOARD
CONTROL - An example for high-resolution SAR-image
113
5 EXPERIMENTAL RESULTS
FOR STRONG BUILDING
HYPOTHESES
This is a methodological contribution meant to
stimulate discussion on how to organize
intermediate processes in computer vision. Human
subjects are usually not aware of these intermediate
processes – while performing them. This obviously
presents a remarkable cognitive achievement. The
system presented does not extract buildings from
high resolution SAR-images. These higher level
decisions are preserved for later work based on the
results presented here.
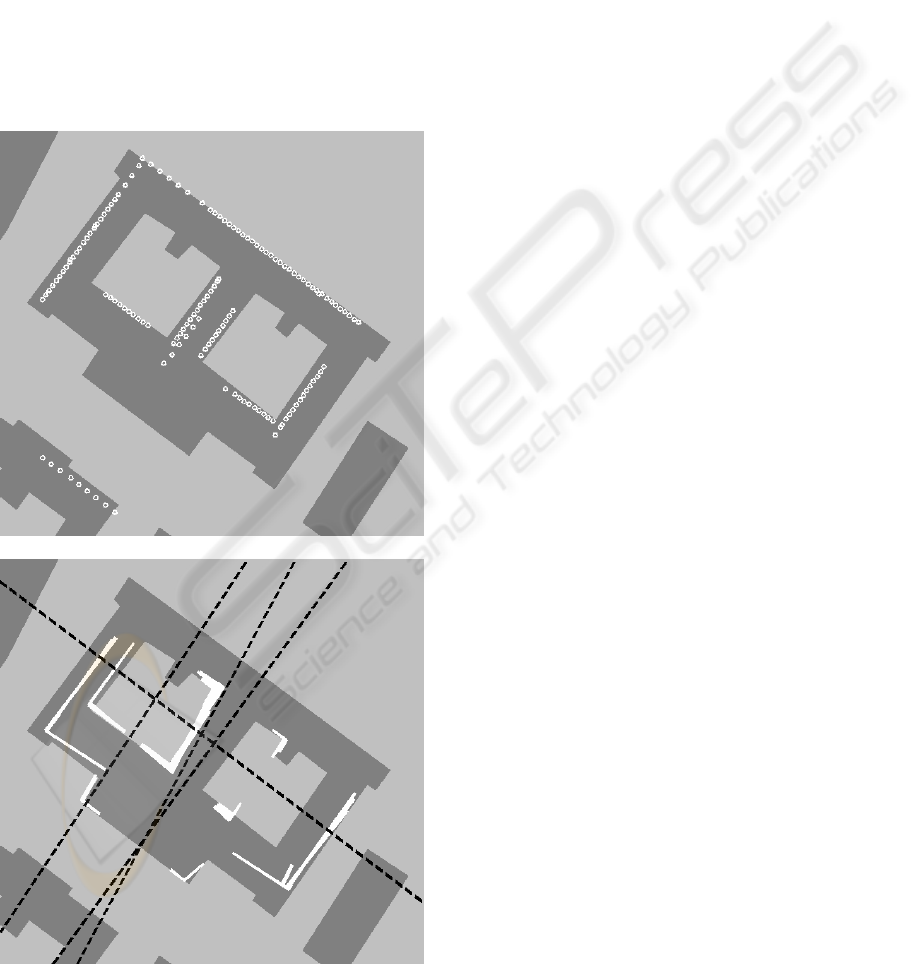
Figure 6: Results overlayed to a GIS-building layer ground
truth.
Assessments on the issue of appropriateness for
remote sensing tasks need systematic testing and
comparison with other methods on a representative
dataset and definition of goals. There simply is not
enough such high resolution SAR imagery around to
start this yet.
To demonstrate any-time capability the search
run was terminated after 40000 interpretation cycles.
At that stage the queue was still filled with many
thousand working elements and growing. Fig. 6
shows the encouraging results. These results confirm
the assessment driven ansatz as appropriate tool for
perceptive building cue detection.
For better judgement the building layer of a GIS-
base of the imaged campus area was chosen as
background for the figures. All major rows of strong
scatteres have been detected. Symmetry objects were
clustered after the search using homogenous straight
representation for the axis. The main symmetry axis
of the building are detected (dashed black lines).
Moreover, even all symmetries of the left yard are
present. Objects A participating in the objects Sy
are coloured white.
3 DISCUSSION AND
CONCLUSION
Citing form the research roadmap (ECVision, 2005)
we affirm that: “... The very essence of the
cognitivist approach is that cognition comprises
computational operations defined over symbolic
representations and these computational operations
are not tied to any given instantiation. ...” (Section
6.1.2, page 29). This is what production-nets are
about.
For next generation SAR-data an intermediate
grouping process seems appropriate between feature
extraction and final decision or description for
automatic vision. Particularly the very high
resolution devices generate imagery for which this is
essential. Standard grouping techniques like
clustering for local constraints like proximity and
Hough transform or tensor voting for good
continuation lack the flexibility and
cooperative/competitive structure of the method
presented here. On the other hand complex high-
level AI reasoning schemes may not be capable of
handling large amounts of data in a robust and quick
way. The accumulative production-net search turns
out a reasonable alternative for such tasks.
Repetitive structure and symmetry constitute
strong relations that improve building detection
VISAPP 2006 - IMAGE UNDERSTANDING
114

significantly. The proposed production system with
its accumulative control enables modular and robust
utilization of these perceptive properties. Objectives
of future work include symmetry of more complex
objects e.g. generic descriptions of building parts.
This leads also to theoretic investigations concerning
decision theoretic inference of the constraint
relations, computational complexity estimation and
stop criteria.
ACKNOWLEDGEMENTS
We thank Dr. J. H. G. Ender and Dr. A. R Brenner
from FGAN-FHR for providing us with the PAMIR
SAR-data.
REFERENCES
Cohn, A. G., Magee, D., Galata, A., Hogg, D., Hazarika,
S. 2003. Towards an architecture for cognitive vision
using qualitative spatio-temporal representations and
abduction. In: Freksa, C., Brauer, W., Habel, C.,
Wender, K. F. (eds.) Spatial Cognition III, Routes and
Navigation, Human Memory and Learning, Spatial
Representation and Spatial Learning, Springer, Berlin
pp. 232-248.
Ender, J. H. G., Brenner, A. R., 2003. PAMIR - a
wideband phased array SAR/MTI system. In: IEE
Proceedings - Radar, Sonar, Navigation, Vol. 150, no.
3, pp. 165-172.
Foerstner, W., 1994. A framework for low level feature
extraction. In: Eklundh, J.-O. (ed). Computer Vision –
ECCV 94. Vol. II, B1, pp. 383-394.
Guo, C.-E., Zhu, S.C., Wu, Y. N. 2003. Modelling visual
patterns by integrating descriptive and generative
methods, IJCV, Vol. 53, No. 1, pp. 5-29.
Draper, B., Collins, R., Brolio, J., Hanson, A., Riseman, E.
1989. The Schema System, IJCV, Vol. 2, pp. 209-250.
Klausing, H., Holpp, W., 2000. Radar mit realer und
synthetischer Apertur, Oldenburg Verlag, München.
Laptev, I., Mayer, H., Lindeberg, T., Eckstein, W., Steger,
C., Baumgartner, A., 2000. Automatic Extraction of
Roads from Aerial Images Based on Scale Space and
Snakes, Machine Vision and Applications, Vol. 12,
No. 1, pp. 22-31.
Leavers, V. F., 1993. Which Hough transform? CVGIP,
Image Understanding, Vol. 58, No. 2, pp. 250-264.
Lowe, D., G., 1985. Perceptual organization and visual
recognition, Kluwer, Boston.
Marr, D., 1982. Vision, Freeman, San Francisco.
Matsuyama, T., Hwang, V. S.-S., 1990. Sigma a
knowledge-based image understanding system,
Plenum Press, New York.
Medioni, G., Lee, M., Tang, C., 2000. A computational
framework for segmentation and grouping. Elsevier,
Amsterdam.
Michaelsen E. 1998a. Über Koordinaten Grammatiken zur
Bildverarbeitung und Szenenanalyse. Diss., Univ. of
Erlangen, available online as
www.exemichaelsen.de/Michaelsen_Diss.pdf
Michaelsen E., Stilla U. 1998b. Remark on the notation of
coordinate grammers. In: Armin A., Dori D., Pudil P.,
Freeman H. (eds.) Advances in pattern recognition,
JOINT IAPR Int. Workshop SPR-SSPR. Springer,
Berlin, pp. 421-428
Michaelsen E., Stilla U. 2002. Probabilistic Decisions in
Production Nets: An Example from Vehicle
Recognition. In: Caelli T., Amin A., Duin R. P. W.,
Kamel M., Ridder D. de (eds): Structural, Syntactic
and Statistical Pattern Recognition SSPR/SPR 2002,
LNCS 2396, Springer, Berlin, pp. 225-233.
Michaelsen, E., Soergel, U. Stilla, U., 2002. Grouping
salient scatterers in InSAR data for recognition of
industrial buildings. In: Kasturi, R., Laurendeau, D.,
Sun, C. (eds). 16th Int. Conf. on Pattern Recognition,
ICPR 2002. Vol. II, pp. 613-616.
Michaelsen, E., Middelmann, W., Sörgel, U.,
Thönnessen, U. 2005. On the improvement of
structural detection of building features in high-
resolution SAR data by edge preserving image
enhancement.
Pattern Recognition and Image
Analysis, MAIK, NAUKA, Moscow, Vol. 15, No. 4, pp.
686-689.
Stilla U., Michaelsen E., Lütjen K. 1996. Automatic
Extraction of Buildings from Aerial Images. In: F.
Leberl, R. Kalliany, M. Gruber (eds.), Mapping
Buildings, Roads and other Man-made Structures from
Images, IAPR-TC7, Wien, Oldenburg, pp. 229-244.
Wertheimer, M., 1923. Untersuchungen zur Lehre von der
Gestalt II. Psychol. Forsch., Vol. 4. Translated as
‘Principles of Perceptual Organization’ In: Beardslee,
D., Wertheimer M., 1958 (eds.), Princeton, N. J. pp
115-135.
ECVision: European research network for cognitive vision
systems, 2005. A research roadmap of cognitive
vision. www.ecvision.org.
COGNITIVE VISION AND PECEPTUAL GROUPING BY PRODUCTION SYSTEMS WITH BLACKBOARD
CONTROL - An example for high-resolution SAR-image
115
