
RECONSTRUCTION OF ELLIPSOIDS ON ROLLERS FROM
STEREO IMAGES USING OCCLUDING CONTOURS
Sudanthi N.R. Wijewickrema and Andrew P. Papli
´
nski
Clayton School of Information Technology
Monash University, Victoria, 3800, Australia
Charles E. Esson
Colour Vision Systems Pty Ltd
11 Park Street, Bacchus Marsh, Victoria, 3340, Australia
Keywords:
Quadric Reconstruction, Ellipsoid Modelling, Occluding Contours, Fruit Sorting.
Abstract:
We describe the reconstruction of quadric surfaces with special attention on ellipsoids, using two different
views from calibrated cameras, given that they rest on known objects in space. The technique proposed
focuses basically on speed and efficiency and is suitable to be used in resource constrained environments in
real time.
We model the quadric in dual space and introduce a method of including application specific information in
the reconstruction. We also discuss a novel and fast way of adjusting the occluding contours to fit the epipolar
tangency constraints before the reconstruction. We further apply this to a real-life application where ellipsoidal
fruits are modelled in 3d. Then, we analyze the error of fit for the reconstructed quadrics. Although this paper
focuses on ellipsoids, it can be easily extended to incorporate the modelling of other non-degenerate quadrics
using two occluding contours in dual space.
1 INTRODUCTION
Reconstruction of quadric surfaces from occluding
contours is essential when dealing with non-textured
smooth surfaces where correspondence between fea-
tures cannot be obtained. Early works of this kind in-
clude (Giblin and Weiss, 1987) where the profiles of
a smooth surface was used in the reconstruction given
that the motion of the camera was small, known and
coplanar. Another approach to surface reconstruction
was later developed that could incorporate large vari-
ations of camera motion between views (Ma and Li,
1996; Mendonca et al., 2000). These were further
developed to include unknown camera motion (Cross
et al., 1999; Mendonca et al., 2000).
(Ma and Chen, 1994) introduced a non-linear re-
construction method for quadrics using perspective
views. (Ma and Li, 1996) builds on (Ma and Chen,
1994) and (Karl et al., 1994), which discusses the
reconstruction of ellipsoid surfaces from the silhou-
ettes of its orthographic projections. Both (Karl et al.,
1994) and (Ma and Li, 1996) investigate the special
case of reconstructing ellipsoids and the former shows
how this can be done with three or more orthogonal
views. The latter uses three perspective views and for
calibrated cameras, it is a linear calculation.
Techniques such as (Cross and Zisserman, 1998)
use the duality property of points and planes in the
homogeneous coordinate system. (Cross, 2000) dis-
cusses 3d surface reconstruction in detail for sin-
gle and multiple view cases and explains the use of
occluding contours in dual space and/or additional
points/planes in the calculation. (Kang et al., 2001;
Kang et al., 2003) use occluding contours to calcu-
late the tangent planes to the surface and perform the
fitting of a dual quadric in the space of planes.
The aim of this paper is to discuss a method of
quadric surface reconstruction using occluding con-
tours of two perspective images focusing on the spe-
cial case of ellipsoids. Among others, we build on
the work of (Cross and Zisserman, 1998) and (Cross,
2000). The main focus of this algorithm is to maxi-
mize efficiency. Hence, it avoids non-linear iterative
methods and searching techniques (e.g. finding corre-
spondence). The desired application requires higher
speed, that leads to resource constraints. The solu-
tions obtained here are suitable for such an environ-
ment.
370
N. R. Wijewickrema S., P. Papli
´
nki A. and E. Esson C. (2006).
RECONSTRUCTION OF ELLIPSOIDS ON ROLLERS FROM STEREO IMAGES USING OCCLUDING CONTOURS.
In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 370-376
DOI: 10.5220/0001366903700376
Copyright
c
SciTePress

2 OVERVIEW
This section gives an overview of the method used
in the quadric reconstruction and how the paper is
structured. The algorithm uses images taken from
two non-concentric, calibrated cameras, fits conics to
them and reconstructs the quadric with the use of ad-
ditional information. The technique can be summa-
rized as follows:
• Fit conics to the projections (images)
• Align the two fitted conics so that they adhere to
the epipolar geometry
• Reconstruct the family of quadrics in dual space
• Select a quadric that sits on one or more known
quadric surfaces
The rest of the paper explains this method in detail.
Section 3 discusses quadrics and the duality princi-
ple and then goes on to explain how the reconstruc-
tion is done in dual space. Section 4 discusses how
to introduce application specific information into the
calculation. Section 5 addresses the implementation
specific problem of the conics not fitting epipolar tan-
gency constraints. It introduces an algorithm to ad-
just them accordingly. Then, experimental results are
given in Section 6 where the algorithm is applied to
data obtained from fruit sorting applications.
3 QUADRICS AND DUAL SPACES
A quadric is a surface in 3d, represented by a 4 × 4
symmetric matrix Q. For each point X on the sur-
face, represented by a homogeneous coordinate vec-
tor X = [x y z 1]
T
, the following condition should
be satisfied.
X
T
QX = 0 (1)
The pole-polar relationship for a quadric is defined as
follows. If X is a point anywhere in space, then there
exists a plane π satisfying the condition in eqn (2).
Then, X is the pole and π is the corresponding polar
plane with respect to the quadric Q. If the pole X lies
on the surface of the quadric, the polar plane π be-
comes the tangent plane to the quadric at X (Hartley
and Zisserman, 2003).
π = QX (2)
Duality in 3d is expressed as the interchangeability
of points and planes (Bruce, 1992; Hartley and Zis-
serman, 2003). Considering the equation of a plane
π
T
X = 0, we can see that interchanging the 4 ele-
ment vectors would not change the equation. So, by
using eqns (1) and (2), we get the dual quadric Q
∗
which is defined by a set of planes and satisfies the
constraint π
T
Q
∗
π = 0.
Q
∗
= Q
−1
(3)
Alternatively, the dual can be defined as the ad-
joint of the quadric Q
∗
= adj(Q) since adj(Q) =
det(Q)Q
−1
and the scale factor does not affect the
quadric equation.
A conic can be defined in 2d space similar to a
quadric by a 3× 3 symmetric matrix, C. For a point in
2d x represented as a homogeneous vector of three el-
ements lying on the conic, the constraint x
T
Cx = 0
is satisfied. The pole-polar relationship is similar to
the case of a quadric where the pole is a point in 2d
and the polar is a line. l = Cx gives the relationship
between a pole and its polar line and if x is on C,
the polar line is tangent to the conic. Duality between
points and lines exists and a line conic can be defined
as C
∗
= C
−1
or C
∗
= adj(C) with l
T
C
∗
l = 0
The outline of the projection of a quadric (occlud-
ing contour) is the projection of its contour generator.
The contour generator is the curve formed by the tan-
gency between the quadric and the cone of light rays
leading to the camera center. Since the contour gen-
erator arises from tangency, it is more convenient to
use the dual quadric of Q in the determination of the
projected conic. Under the camera matrix P , the pro-
jection of the quadric Q is the conic C given by eqn
(4). Here, Q
∗
and C
∗
are the duals of the quadric and
the conic respectively. Proof of this can be found in
(Hartley and Zisserman, 2003).
C
∗
= P Q
∗
P
T
(4)
A conic and a quadric have 5 and 9 degrees of
freedom respectively. Hence, one projection of the
quadric would impose 5 constraints on the recon-
struction. In other words, the dual of the occluding
contour conic defines 5 independent planes that the
dual quadric has to be tangent to. In the case of two
cameras though, epipolar tangency constraints dictate
that the two tangent cones generated by the two cam-
eras share two planes. Hence, in the case of two
views only 8 constraints are imposed on the quadric.
This indicates that given two views from two non-
concentric cameras, we can obtain a family of dual
quadrics as shown in eqn (5), where λ is a parame-
ter and Q
∗
1
and Q
∗
2
are known. Details of this can be
found in (Cross and Zisserman, 1998; Cross, 2000).
Q
∗
(λ) = Q
∗
1
+ λQ
∗
2
(5)
4 TANGENCY INFORMATION
Section 3 explains the reconstruction of a family of
quadrics. To remove the ambiguity, we need to intro-
RECONSTRUCTION OF ELLIPSOIDS ON ROLLERS FROM STEREO IMAGES USING OCCLUDING CONTOURS
371

duce additional information such as another tangent
plane or points on the surface. If point information is
introduced, eqn (5) has to be inverted to get the family
of quadrics in real space giving us a cubic equation in
λ. Hence, solving the ambiguity in dual space is much
simpler and more efficient.
We use the fact that most quadric surfaces in real
life would rest on some known surface, be it a plane
or another quadric in space. If the surface is a plane
(say π
k
), the unique quadric could be reconstructed
easily by using π
T
k
Q
∗
π
k
= 0, giving us a value for λ
as follows:
λ
k
= −
π
T
k
Q
∗
1
π
k
π
T
k
Q
∗
2
π
k
(6)
But in most situations, we might just know one or
more other quadric surfaces that the quadric to be re-
constructed is tangent to. We discuss a simple cal-
culation to be used in such situations. For example,
we consider a case where the quadric lies on a set of
rollers (cylinders or cones).
In such cases, we use the fact that the quadric must
rest on some plane parallel to the xy plane between a
range of heights. The range of heights should be de-
termined from the size and orientation of the known
quadrics. For each of these heights, we calculate the
plane π
k
parallel to the xy plane and using eqn (6),
get a unique dual quadric. Then for each of these dual
quadrics, we check for tangency with one or more
known quadrics in space. The following section de-
scribes how this is done in a fast and efficient manner.
4.1 Tangency Between Quadrics
Let the quadric to be reconstructed be Q
w
and the
known surface in space be Q
k
. For the scope of this
calculation, Q
k
could be any non-degenerate or de-
generate quadric while Q
w
should be non-degenerate.
Let X be any pole with respect to both quadrics and
π be the respective polar plane. Then, the relation-
ships in eqn (7) holds. Note that both equations give
the same plane since the scale factor µ does not affect
the equation of the plane.
π = µQ
w
X
π = Q
k
X
(7)
(µQ
w
− Qk)X = 0 =⇒ (µI − P )X = 0 (8)
Where,
P = Q
−1
w
Q
k
and I is the 4 × 4 identity matrix
This is an eigensystem which has four solutions that
gives the common poles (values of X) to the two
quadrics Q
w
and Q
k
. By substituting them in eqn
(7), we get the respective polar planes.
Tangent Quadrics
Coincident
Polar Planes
Coincident
Poles
Figure 1: Tangent Quadrics and coinciding Poles/Polar
Planes.
It was observed that if the quadrics are tangent to
each other, out of these four solutions, two poles (and
hence, the respective polar planes) coincide. In this
case, the coincident poles lie on the surfaces of both
Q
w
and Q
k
fulfilling the tangency requirement given
in eqn (2). Figure 1 shows how two poles and polar
planes coincide in a case of tangency.
5 CONIC ADJUSTMENT
To obtain the occluding contour of the projection,
conics have to be fitted to the projected images. For
this, any suitable conic fitting algorithm could be
used. We use the ellipse specific algorithm discussed
in (Wijewickrema and Papli
´
nski, 2005) as it is more
suited for the type of application this is aimed for.
It does not require edge detection (but only a sim-
ple segmentation of the object from the background)
and uses a subset of points inside the object making it
more robust against outliers.
In real applications, the fitted conics may not ad-
here to epipolar tangency constraints due to errors in
fitting and the fact that the objects may not be ideal
ellipsoids. Hence, a conic correction algorithm has to
be applied on the fitted conics before the reconstruc-
tion. (Cross, 2000) discusses a method of non-linear
optimization using the Levenberg-Marquardt method
for this adjustment. Alternatively, we use a more ef-
ficient algorithm for conic adjustment using frontier
points as discussed in the following section.
5.1 Frontier Points
The concept of frontier points was first introduced in
(Rieger, 1986), and was interpreted in (Porril and Pol-
lard, 1991) as the fixed point on the surface of the
VISAPP 2006 - MOTION, TRACKING AND STEREO VISION
372

Tangent Plane at P
s
P
n
n
Cones
Quadric
L
R
O
O
Figure 2: Tangent Plane at a Frontier Point.
quadric, corresponding to the intersection of two cor-
responding contour generators. Frontier points lie on
the epipolar planes shared by the two tangent cones.
This is explained in the Occluding Edge Theorem
given in (Collins et al., 2004). It states that at the
frontier points, the tangents to the two cones and the
quadric coincide. Figure 2 shows this relationship.
We further this theorem by using the following corol-
lary.
Corollary 1: The tangent plane at a frontier point
P to the cones and the quadric, contains the vector
s joining the two cameras and the rays passing from
either camera center to P. Hence, the normal n, to
the tangent plane at P and s are orthogonal. That is:
s
T
n = 0 (9)
A cone is a degenerate quadric and hence could be
represented using a 4 × 4 symmetric matrix that sat-
isfies eqn (1). If it is represented by the matrix R, the
normal n to the cone at a point X would be as shown
in eqn (10), where
¯
R is a 3 × 4 matrix consisting of
the first three rows of R.
n = 2
¯
RX (10)
Hence, at a frontier point X
f
, the normals n
L
and n
R
to the two tangent cones R
L
and R
R
would satisfy
eqn (9), giving us eqn (11).
AX
f
= 0 with A =
s
T
¯
R
L
s
T
¯
R
R
(11)
A is a 2 × 4 matrix, the (right) null space of which
gives a one-parameter family of solutions for X
f
as
given in eqn (12). Here X
f1
and X
f2
are four element
vectors and γ is a scalar parameter.
X
f
= X
f1
+ γX
f2
(12)
Since the frontier points lie on the surface of the
cones, eqn (12) has to satisfy eqn (1) which would
yield a quadratic equation in γ. Solving for γ and
substituting in eqn (12) gives the two frontier points.
Since the plane under consideration is tangent to
the quadric, its projection on the image plane would
be tangent to the projected conic (occluding contour).
The point of contact of the conic and the tangent line
is the projection of the frontier point. The epipole
lies on this same tangent line because the tangent
plane contains the camera center of the other cam-
era as shown above. Hence, the tangents drawn from
the epipole to the conics should correspond over the
two images (same plane projected on the two image
planes). That is, they should adhere to the epipolar
geometry (Hartley and Zisserman, 2003). This is the
epipolar tangency constraint that the conics have to
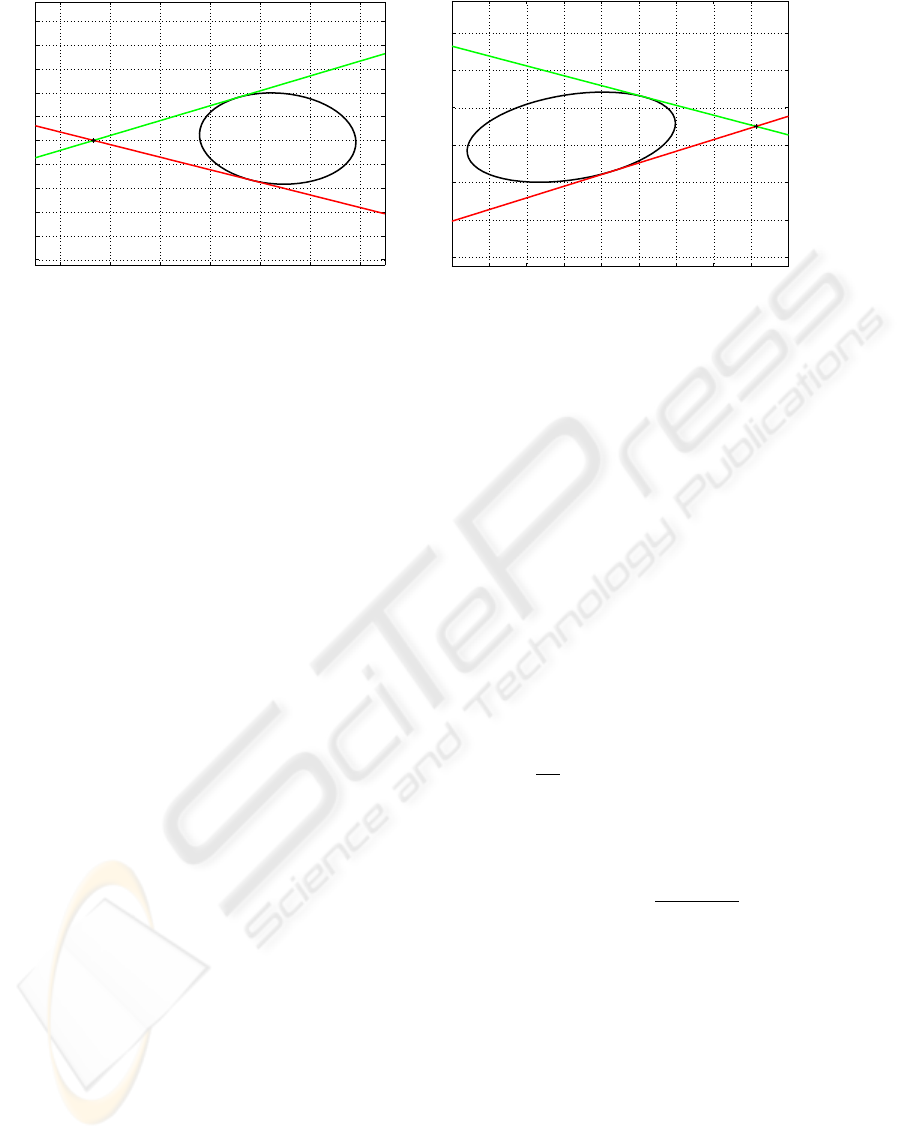
satisfy. Figure 3 shows this relationship where e
L
and
e
R
are the epipoles and l
L1
, l
L2
, l
R1
and l
R2
are the
corresponding epipolar tangents.
It could be seen that, if the projected conics satisfy
this constraint, the points obtained from substituting
the values of γ to either cone would yield the same
results. If not, they would essentially be different.
5.1.1 Conic Adjustment Algorithm
As mentioned above, if the projected conics do not
satisfy the epipolar tangency constraints, we get dif-
ferent sets of values for the frontier points when sub-
stituting to the equations of the two cones. For the
scope of our application, where the deviation is not
large enough to warrant iterative optimization meth-
ods, we assume that the mean of the two sets gives a
reasonable approximation.
Thus, we have two points in space that (we assume)
lie on both contour generators and hence we know
that they would be on the projected conic contours
as well. Further they would be on the common tan-
gent plane and hence the epipolar lines drawn through
these projected points should be tangent to the conic
as well. We use this property in the adjustment of the
conics.
We need to find the conic that goes through the pro-
jected frontier points p
1
and p
2
while being tangent
to the epipolar lines l
1
and l
2
at the same points. The
tangents to the conic C can be written as shown in eqn
(13), where α
i
are scalars constants.
α
1
l
1
= Cp
1
α
2
l
2
= Cp
2
(13)
By row scanning the conic matrix C, and using only
its unique elements, we get a vector c. Let the points
and lines be represented by p
i
= [p
i1
p
i2
p
i3
] and
l
i
= [l
i1
l
i2
l
i3
] respectively, with i = 1, 2. They
RECONSTRUCTION OF ELLIPSOIDS ON ROLLERS FROM STEREO IMAGES USING OCCLUDING CONTOURS
373
−20 −10 0 10 20 30 40
−20
−15
−10
−5
0
5
10
15
20
25
30
e
L
C
L
l
l
p
p
L1
L2
L1
L2
−60 −50 −40 −30 −20 −10 0 10 20 30
−30
−20
−10
0
10
20
30
R
l
l
C
p
p
R
e
R2
R2
R1
R1
Figure 3: The Epipolar Tangency Constraints.
can then be represented in matrix form, P
i
so that eqn
(13) could be written as α
i
l
i
= P
i
c.
c = [c
11
c
12
c
13
c
22
c
23
c
33
]
T
P
i
=
"
p
i1
p
i2
p
i3
0 0 0
0 p
i1
0 p
i2
p
i3
0
0 0 p
i1
0 p
i2
p
i3
#
Then, we can rewrite eqn (13) in the following
form, with ¯α
i
= −α
i
.
Nu = 0
Where,
N =
P
1
l
1
0
P
2
0 l
2
and u =
"
c
¯α
1
¯α
2
#
N is a 6 × 8 matrix of rank 6. Solving for the null
space of N , we get a one-parameter family of vectors.
By considering only the elements related to c, we get
the unique elements of this conic family. Here, c
1
and
c
2
are 6 element vectors and β is a scalar parameter.
c = c
1
+ βc
2
By rearranging the vector c to get the matrix form of
C, we get the family of conics that satisfy the epipolar
tangency constraints.
C = C
1
+ βC
2
(14)
The next step is to select the conic from this family
that suits the fitted conic best. For this, from the equa-
tion of the fitted conic, we generate a set of points
x
i
= [x
i
y
i
1] where x
i
is the i
th
point. We can
also use the set of edge points in this calculation in-
stead of points generated from the fitted conic. Let
the number of points generated be n. First, we calcu-
late the algebraic distance d
i
= x
T
i
Cx
i
of each point
from the family of conics C. From eqn (14), we get:
d
i
= a
i
+ βb
i
Where,
a
i
= x
T
i
C
1
x
i
and b
i
= x
T
i
C
2
x
i
The error e is defined as the sum of squares of alge-
braic distances for all points x
i
.
e =
n
X
i=1
d
2
i
=
n
X
i=1
a
2
i
+ 2β
n
X
i=1
a
i
b
i
+ β
2
n
X
i=1
b
2
i
We need to find the value of the parameter β that min-
imizes the error e. Hence, the following has to be sat-
isfied.
∂e
∂β
= 2(
n
X
i=1
a
i
b
i
+ β
n
X
i=1
b
2
i
) = 0
This gives us the value for β that can be plugged into
eqn (14) to get the best adjusted conic.
β = −
P
n
i=1
a
i
b
i
P
n
i=1
b
2
i
(15)
By applying this to both projected conics, we get a
pair of conics that adhere to the epipolar tangency
constraints. They also ensure that the adjusted conics
are as close to the originally fitted conics as possible.
6 EXAMPLE APPLICATION
We apply our algorithm to data from a real-life appli-
cation: namely fruit sorting. Here the fruits are placed
on rollers whose dimensions and orientation in space
are known. Each fruit rests on four conic rollers and
images are captured by two cameras placed on either
side of the rollers. Images taken from the two cameras
VISAPP 2006 - MOTION, TRACKING AND STEREO VISION
374

50 100 150 200 250 300 350
0
50
100
150
200
250
Adjusted
Ellipse
Fitted
Ellipse
50 100 150 200 250 300 350
0
50
100
150
200
250
Ellipse
FittedAdjusted
Ellipse
Figure 4: Images captured by two cameras with the fitted and adjusted conics.
Reconstructed
Ellipsoid
Rollers (Cones)
Figure 5: Reconstructed Ellipsoid.
along with the fitted and adjusted conics are shown in
figure 4.
The roller information and the adjusted conics are
then used to reconstruct the quadric as explained in
section 3. Such a reconstructed quadric is shown in
figure 5.
6.1 Error Analysis
For the analysis of error, we use two measures: re-
projection error and volume error. The re-projection
error by itself is not a full measure of the error
involved. Any quadric selected from the family
of quadrics reconstructed using eqn (5) would be
projected on the image plane as the same conic.
Hence, the error that is calculated by comparing the
re-projection and the original fitted conic (or edge
points) would just give a measure of the error involved
in conic fitting and adjustment.
Hence, to get a true feel for the reconstruction
error, we need to introduce another measurement.
This is done by comparing the dimensions of the
actual ellipsoid with its reconstructed counter-part.
By calculating the volume of the actual and recon-
structed ellipsoids, we obtain this second error mea-
sure, which along with the re-projection error gives a
more rounded view of the reconstruction error.
For this experiment, we used spheres and ellipsoids
of different dimensions and placed them at different
positions and orientations. Then we calculated the re-
projection and volume errors.
The re-projection error was measured as the nor-
malized sum of squares of algebraic distances from
the fitted conic to the re-projected conic. For n points
on the fitted conic (or edge points), we calculate the
error as given in eqn (16).
e
rep
=
1
n
n
X
i=1
d
2
i
(16)
Where, d
i
is the algebraic distance from the i
th
point
to the re-projected conic.
The volume error was calculated as the percentage
error between the volumes of the actual and recon-
structed ellipsoids. The results are summarized in ta-
ble 1. The re-projection error indicates the mean of
the errors calculated for the left and right images.
7 CONCLUSION
We proposed an algorithm for reconstructing ellip-
soids given two occluding contours of views obtained
from non-concentric cameras. First we adjusted the
conics using a simple calculation as a prerequisite
to the quadric fitting. Then, we discussed how the
method introduced in (Cross and Zisserman, 1998)
RECONSTRUCTION OF ELLIPSOIDS ON ROLLERS FROM STEREO IMAGES USING OCCLUDING CONTOURS
375

Table 1: Error Analysis.
Re-projection Volume
Error(10
−5
) Error(%)
Sphere 1 0.0563 3.1084
Sphere 2 2.0596 3.3040
Sphere 3 2.5063 2.6390
Ellipsoid 1 1.5880 3.4664
Ellipsoid 2 1.3303 3.1677
Ellipsoid 3 1.4047 3.2808
Ellipsoid 4 1.0186 4.8704
could be used to construct a family of quadrics in dual
space. Then we use additional application specific in-
formation so that a unique quadric can be obtained.
The basic advantage of the proposed algorithm is
that it avoids non-linear calculations. This is particu-
larly important in the type of application this is aimed
for. As shown in section 6.1, the errors involved are
quite acceptable and part of that could be contributed
to human errors involved in the obtaining of experi-
mental measurements.
The drawback in this method is that the additional
quadric surface(s), which the quadric to be recon-
structed is tangent to, must be known. This may not
be possible in some situations, making the algorithm
unsuitable. Further, the errors in the measurements
(for example, the distance of the known quadric from
the origin of the world coordinate system), account
for a large percentage of the reconstruction error. This
makes the reconstruction sensitive to human errors.
Future work related to this research is to incorpo-
rate forward movement and rotation of the quadrics
and to model the motion as well as the shape, location
and orientation. Another avenue of research would be
to come up with more accurate representations of the
surfaces and to include texture information as well.
ACKNOWLEDGEMENTS
The authors would like to thank Mr. G.C. De Silva of
Tokyo University, Japan for his invaluable input.
REFERENCES
Bruce, J. W. (1992). Lines, surfaces and duality. Mathe-
matical Proceedings of the Cambridge Philosophical
Society, 112:53–61.
Collins, S., Kozera, R., and Noakes, L. (2004). Shape re-
covery of a strictly convex solid from n-views. In
2nd International Conference on Computer Vision and
Graphics, pages 57–65, Warsaw, Poland.
Cross, G. (2000). Surface Reconstruction from Image Se-
quences: Texture and Apparent Contour Constraints.
PhD thesis, University of Oxford.
Cross, G., Fitzgibbon, A. W., and Zisserman, A. (1999).
Parallax geometry of smooth surfaces in multiple
views. In 7th International Conference on Computer
Vision, pages 323–329, Kerkyra, Greece.
Cross, G. and Zisserman, A. (1998). Quadric reconstuction
from dual-space geometry. In 6th International Con-
ference on Computer Vision, pages 25–31, Bombay,
India.
Giblin, P. and Weiss, R. (1987). Reconstruction of sur-
faces from profiles. In 1st International Conference
on Computer Vision, pages 136–144, London, Eng-
land.
Hartley, R. and Zisserman, A. (2003). Multiple View Geom-
etry in Computer Vision. Cambridge University Press.
Kang, K., Tarel, J.-P., and Cooper, D. (2003). A unified lin-
ear fitting approach for singular and non-singular 3d
quadrics from occluding contours. In 1st International
Workshop on Higher-Level Knowledge in 3D Model-
ing and Motion Analysis, Nice, France.
Kang, K., Tarel, J.-P., Fishman, R., and Cooper, D. (2001).
A linear dual-space approach to 3d reconstruction
from occluding contours using algebraic surfaces. In
8th International Conference on Computer Vision,
pages 136–144, Vancouver, Canada.
Karl, W. C., Verghese, G. C., and Willsky, A. S. (1994).
Reconstructing ellipsoids from projections. CVGIP:
Graphical Model and Image Processing, 56(2):124–
139.
Ma, S. and Chen, X. (1994). Quadric surface reconstruc-
tion from its occluding contours. In 12th Interna-
tional Conference on Pattern Recognition, pages 27–
31, Jerusalem, Israel.
Ma, S. and Li, L. (1996). Ellipsoid reconstruction from
three perspective views. In 13th International Confer-
ence on Pattern Recognition, pages 344–348, Vienna,
Austria.
Mendonca, P. R. S., Wong, K.-Y. K., and Cipolla, R. (2000).
Camera pose estimation and reconstruction from im-
age profiles under circular motion. In 6th Euro-
pean Conference on Computer Vision, pages 864–877,
Dublin, Ireland.
Porril, J. and Pollard, S. (1991). Curve matching and stereo
calibration. Image and Vision Computing, 9(1):45–50.
Rieger, J. (1986). Three dimensional motion from fixed
points of a deforming profile curve. Optics Letters,
11(3):123–125.
Wijewickrema, S. N. R. and Papli
´
nski, A. P. (2005). Prin-
cipal component analysis for the approximation of an
image as an ellipse. In Proceedings of the 13th Con-
ference in Central Europe on Computer Graphics and
Visualization, pages 69–70, Plzen, Czech Republic.
VISAPP 2006 - MOTION, TRACKING AND STEREO VISION
376
