
A FAST ALGORITHM FOR N D POLYHEDRAL SCENE
PERCEPTION FROM A SINGLE 2D LINE DRAWING
Hongbo Li
Key Laboratory of Mathematics Mechanization
Chinese Academy of Sciences, Beijing 100080, China
Lei Huang
Key Laboratory of Mathematics Mechanization
Chinese Academy of Sciences, Beijing 100080, China
Keywords:
nD Perception, Polyhedral Scene, Structural Cognition, 2D Line Drawing, Face Identification.
Abstract:
In this paper, we study the problem of reconstructing the polyhedral structures of a general nD polyhedral
scene from its single 2D line drawing. With the idea of local construction and propagation, we propose a
number of powerfultechniques for general face identification. Our reconstruction algorithm, called “nDView”,
is tested by all the 3D examples we found in the literature, plus a number of 4D and 5D examples we devised.
Our algorithm does not prerequire the dimension n of the object nor the dimension m of its surrounding space
be given, and allows the object to be a non-manifold in which neighboring faces can be coplanar. Another
striking feature is its efficiency: our algorithm can handle 3D solids of over 10,000 faces, with a speed 100
times as fast as the fastest existing algorithms on 2D polyhedral manifold reconstruction.
1 INTRODUCTION
Representing and perceiving an nD object has been
a very fascinating problem in both science and art
(Miyazaki, 1983). For n = 3, the simplest represen-
tation is a line drawing which is the 2D projection of
the wireframe of the object, like drafting in geometric
design and mathematical diagram. To perceive an nD
object one needs to rebuild the nD structure from its
2D projection.
How can the n dimensions be recovered from a rep-
resentation in which almost all dimensions are lost?
To start with, let us analyze how a solid in 3D space
is perceived. No one can direct his eyesight to pierce
through the solid. The only perceived object is the
boundary of the solid, which is a 2D closed manifold.
It is the closedness that allows us to fill the bound-
ary with solid content to achieve one more dimension.
When we watch a line drawing of the wireframe of a
solid, which is essentially one dimensional, we ex-
tract each cycle of edges, either fill it by a plane or by
some other surface to improve its dimension by one.
Then we detect if any closed manifold is formed by
the planes and surfaces, and if so, gain one more di-
mension by filling the closed manifold with solid con-
tent. The closedness of a manifold and a pattern to fill
it are the two essential things in our 3D perception
from low dimensional data. The following concept
generalizes this observation to nD object perception.
The wireframe model of an nD object consists of
(1) a set of edges connecting a finite set of points,
called vertices of the object, (2) a subset of rD cycles
for 0 < r < n, called boundary rD cycles, which are
the boundaries of the (r+1)D pieces of the object, (3)
a set of filling patterns, each for a boundary rD cycle.
The simplest fillings are affine flats. The correspond-
ing wireframe models are called polyhedral scenes.
They can be used to approximate other shapes and
thus are among the most thoroughly studied models.
In this paper we consider only such models.
A transparent line drawing of a wireframe model
is the image of a perspective or parallel projection
from the surrounding mD affine space of the wire-
frame model to the image plane, such that all the
edges and vertices are revealed, and if three vertices
are not collinear in the mD space, nor should their
images.
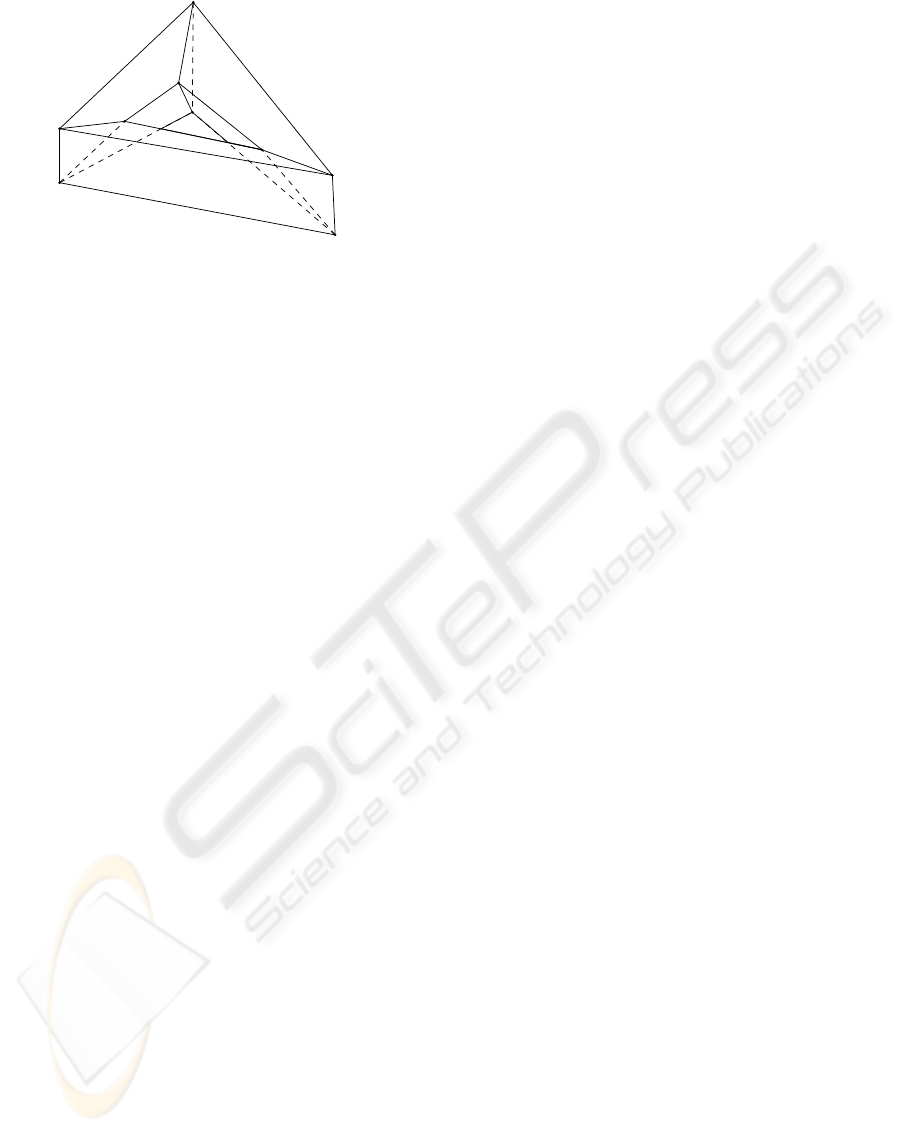
Figure 1 shows a (transparent) line drawing of a
torus in 3D space. It has 6 triangular cycles and 9
square cycles of edges. If all the 15 cycles of edges
are interpreted as polyhedral faces, then the 2D faces
form 6 cycles of faces which are the boundaries of 6
triangular columns. If the 6 cycles of faces are inter-
preted as triangular columns then they form a cycle of
3D faces, which is the boundary of a 4D ball, i.e., the
cycle of 3D faces forms a 3D sphere. So if the object
69
Li H. and Huang L. (2006).
A FAST ALGORITHM FOR N D POLYHEDRAL SCENE PERCEPTION FROM A SINGLE 2D LINE DRAWING.
In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 69-76
DOI: 10.5220/0001363100690076
Copyright
c
SciTePress
F3"
F3
F2"
F2
F1"
F1’
F3’
F2’
F1
V1
V2
V3
V2"
V3"
V1’
V2’
V3’
V1"
Figure 1: A torus in 3D space.
is required to be a 3D manifold, then the line draw-
ing has a unique interpretation which is a 3D sphere.
On the other hand, if the object is required to be a 2D
manifold, then the line drawing has another unique in-
terpretation, which is a torus in which the 6 triangular
cycles are hollow instead of being filled.
This example shows that the problem of wireframe
reconstruction from a single line drawing is rather
“ill-posed”: without a priori knowledge on the shape
and dimension, any cycle can be either filled up or
hollow, and the result is always a solution. What is
the criterion for a “most plausible solution”?
There are three cases each with its own criterion.
The first case is on a single 2D manifold in 3D space
(Liu et al., 2002). Most applications, e.g., the drafting
of machine parts, belong to this case. The criterion
is that all given vertices and edges must be included
in a 2D manifold such that the neighborhood of every
vertex and edge is homeomorphic to a disc. The sec-
ond case is on objects in 3D world in which no two
neighboring faces are coplanar. The criterion for an
optimal solution is that it should be most likely iden-
tified by a human being. Quantitatively this criterion
is described as follows (Shpitalni and Lipson, 1996):
There should be as many faces as possible passing
through as many edges as possible. The third case is
the most general one: we consider polyhedral scenes
of maximal dimension n in an mD surrounding space
in which neither m nor n is given, the objects need
not be a single manifold and two neighboring faces
can be coplanar. In Section 2 of this paper, a principle
of psychological selection is proposed as the criterion
for optimal solution in this case.
For several decades, the study of wireframe models
and their reconstructions has been an active research
topic in computer-aided design, computer graphics
and computer vision (Agarwel and Waggenspack,
1992), (Ganter and Uicker, 1983), (Courter and
Brewer, 1986), (Hanrahan, 1982), (Marill, 1991). In
the literature, all algorithms for 3D reconstruction
consist of two steps: searching for all the cycles in the
wireframe which are face candidates, and then iden-
tifying faces from the candidates. Each step has ex-
ponential complexity, so the reconstruction from 2D
to 3D has double exponential complexity. Since the
problem is NP-complete theoretically, most research
focuses on improving the practical efficiency by re-
ducing the number of potential faces produced in the
first step, i.e., in cycle searching. However, all the al-
gorithms in the literature are global in that the search-
ing is within the whole wireframe. A consequence
is that the number of potential faces is usually much
larger than the number of real faces. There remains a
lot of room for further improvement in efficiency.
In this paper, we first extend the study of polyhe-
dral scene reconstruction from 3D to nD, under the
most general assumption that neither the dimension
n of the object nor the dimension m of its surround-
ing space is given, and whether or not the object is a
manifold is unknown. We then propose several pow-
erful new techniques for face identification, and de-
sign an algorithm for fast and general face identifica-
tion. Among the new techniques, the most prominent
one is localization, i.e., the cycle searching and face
identification are carried out locally and the results are
propagated locally. In the classical case m = n = 3,
our algorithm can handle complicated 3D objects of
over 10,000 faces, outperforming all other algorithms
in both speed and range of application. For the exam-
ples in (Liu and Lee, 2001), (Liu et al., 2002), (Sh-
pitalni and Lipson, 1996), our algorithm can generate
all the solutions for ambiguous wireframes, and pro-
duces much fewer redundant cycles which are not real
faces.
The study of general nD scene reconstruction from
a single line drawing is valuable at least in scien-
tific visualization and high-dimensional animation in
entertainment industry: scientists and artists may be
very much excited to find that their conceptual and
spiritual nD object be readily embodied in, perceiv-
able and recognizable from a single 2D line drawing.
2 N D POLYHEDRAL SCENE
COGNITION
2.1 Constraints on Line Drawings
A perspective projection from mD to 2D is the com-
position of m − 2 successive perspective projec-
tions whose projective centers are linearly indepen-
dent vectors, and at least one center is an affine point.
A parallel projection from mD to 2D is the compo-
sition of m − 2 successive parallel projections whose
projective centers are linearly independent directions.
A naive way of visualizing such a projection is to
imagine watching a TV program, in which there is
VISAPP 2006 - IMAGE UNDERSTANDING
70
a guy watching another TV program, and in that TV
program there is still another guy watching still an-
other TV program, etc. If each TV program is ob-
tained by a pinhole camera through perspective pro-
jection, then the m − 2 successive perspective projec-
tions transforms the mD world into a 2D image.
The reconstruction is the inverse procedure of the
above sequence of projections: the input is the 0D
and 1D information displayed in a 2D space: vertices
and edges of the polyhedral scene; the reconstruction
from 2D to 3D is to identify the real 2D faces of the
scene; going this way, the reconstruction from (m −
1)D to mD is to identify the real (m − 1)D faces.
In a wireframe model, a 0D face is a vertex, a 0D
cycle is the two vertices of an edge, and a 1D face is an
edge. For r > 0, an rD cycle is a set of rD faces such
that (1) if two faces intersect, the intersection belongs
to their iD faces for 0 ≤ i < r, (2) any (r − 1)D face
of one rD face is shared by exactly one other rD face
in the set. For r > 1, an rD face is an (r − 1)D cycle
filled by the rD affine flat surrounded by it.
If two rD faces share at least two (r − 1)D faces
which are in different (r − 1)D planes, then the two
rD faces must be in the same rD affine plane, i.e.,
coplanar. The union of a set of rD coplanar faces
is called an rD polyface, and the faces are said to be
merged together. An advantage of this concept is that
usually we do not need to decompose a polyface into
non-overlapping faces.
Some geometric constraints must be satisfied for
an (r − 1)D cycle to be eligible for being an rD face.
In previous work on face identification, it is gener-
ally assumed that any two neighboring faces are not
coplanar. We feel that this is too strong a constraint to
include many interesting models, so we discard it.
A
B
C
D
E
F
G
H
I
J
K
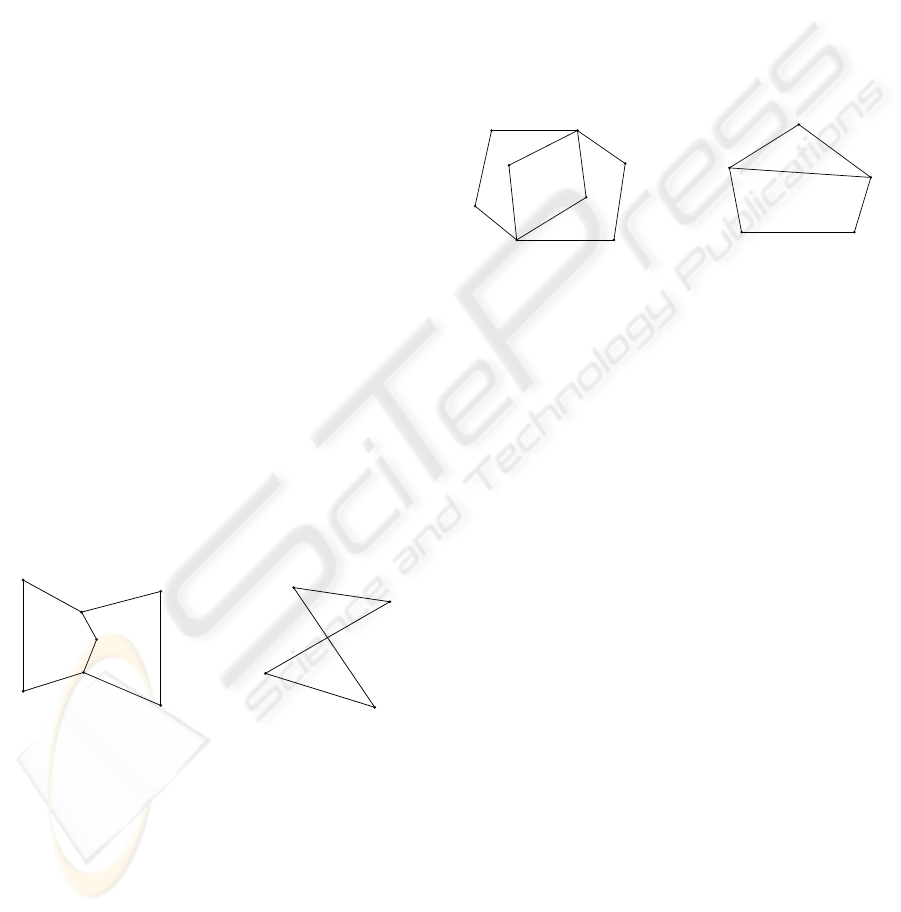
Figure 2: Face adjacency constraint (left: if both ACDEB
and F CDEG are 2D faces then they must be coplanar);
Non-self-intersection constraint (right: since edges HI and
J K intersect not at a vertex, cycle H I JK cannot be the
projection of a 2D face).
The polyhedral setting imposes a strong constraint,
called the rD face adjacency constraint (Shpitalni and
Lipson, 1996): if two rD faces share two (r − 1)D
faces which are in different (r − 1)D affine planes,
then the two rD faces must be in the same rD affine
plane, i.e., are coplanar.
In a line drawing of an mD polyhedral scene, if two
edges are collinear, so are they in the mD scene; if
two edges cross not at a vertex, they do not intersect
in the mD scene. By a perspective projection, a 2D
face is projected onto a 2D region of the image plane
whose boundary does not intersect itself. The 2D non-
self-intersection constraint says that if two edges in-
tersect not at a vertex, then they cannot belong to the
same 1D cycle.
The 2D non-interior-intersection constraint (Liu
et al., 2002) says that if two 1D cycles intersect at
only two vertices and the line segment between the
two vertices intersects both the enclosed regions of
the 1D cycles in the image plane, then either the two
cycles form a polyface, i.e., are coplanar, or at most
one can be assigned as a face.
A
B
C
D
E
F
G
H
I
J
K
L
M
Figure 3: Non-interior-intersection constraint (left: If both
ABC DE and H GC F E are 2D faces then they must be
coplanar, otherwise their intersection CE must be a visible
edge); Chordless constraint (right: cycle IJ LM K contains
a chord J K, so it is not assigned as a face, instead, I JK
and J LM K can be assigned as faces).
If an rD face F does not belong to an rD cycle C
but its intersection with C is exactly the boundary of
F , then F is called a chord of C. A face with chord
can always be decomposed along its chord into two
coplanar faces, and can thus be replaced by the two
faces sharing the chord. However, the two faces need
not be coplanar any more. To gain more degree of
freedom in the reconstruction, an rD cycle with chord
is not assigned as a face. This is the rD chordless
constraint.
2.2 Principle of Psychological
Selection
For a general object in an unknown environment, a
human tends to choose a face identification in which
there are as many edges as possible participating in
as many faces as possible, which is the guideline for
the algorithms in (Liu and Lee, 2001) and (Shpitalni
and Lipson, 1996). If the dimension is unknown, the
most important goal should be to find the highest di-
mension n, for which the above guideline may not be
helpful.
Our principle of psychological selection is that for
r > 1, the rD face identification should make as
many (r − 1)D faces as possible participating in as
many rD faces as possible, such that the sequence of
A FAST ALGORITHM FOR ND POLYHEDRAL SCENE PERCEPTION FROM A SINGLE 2D LINE DRAWING
71

numbers of non-coplanar iD faces is maximal lexico-
graphically, for i from n down to r.
For example, if a line drawing has two explana-
tions, one is two 3D faces together with fifty 2D faces
not belonging to the 3D faces, the other is one 3D face
together with one hundred 2D faces not belonging to
the 3D face, such that any two faces of the same di-
mension are not coplanar, then it is the former expla-
nation that is chosen as the optimal solution. Thus,
our principle of psychological selection is different
from that in (Liu and Lee, 2001) and (Shpitalni and
Lipson, 1996). Its goal is to find first the highest di-
mension n, second as many as possible nD faces that
are non-coplanar.
2.3 Principle of Rigidity
To improve the speed for finding the first optimal so-
lution, it is very important to arrange the face can-
didates in such an order that the most plausible ones
come first. We classify the cycles according to their
rigidity so that they have different levels of priority in
face identification.
By the definition of a cycle, the supporting affine
plane of an (r − 1)D cycle has dimension at least r.
If in the geometric reconstruction from rD to (r +
1)D, for a given (r −1)D cycle in the rD affine plane,
the dimension of the configuration space of the lifted
cycle is k + r + 1, then the rigidity of the cycle is
defined to be −k, and the flexibility of the cycle is
defined to be k. A cycle of rigidity 0, or −1, or < −1
is said to be rigid, or elastic, or plastic respectively.
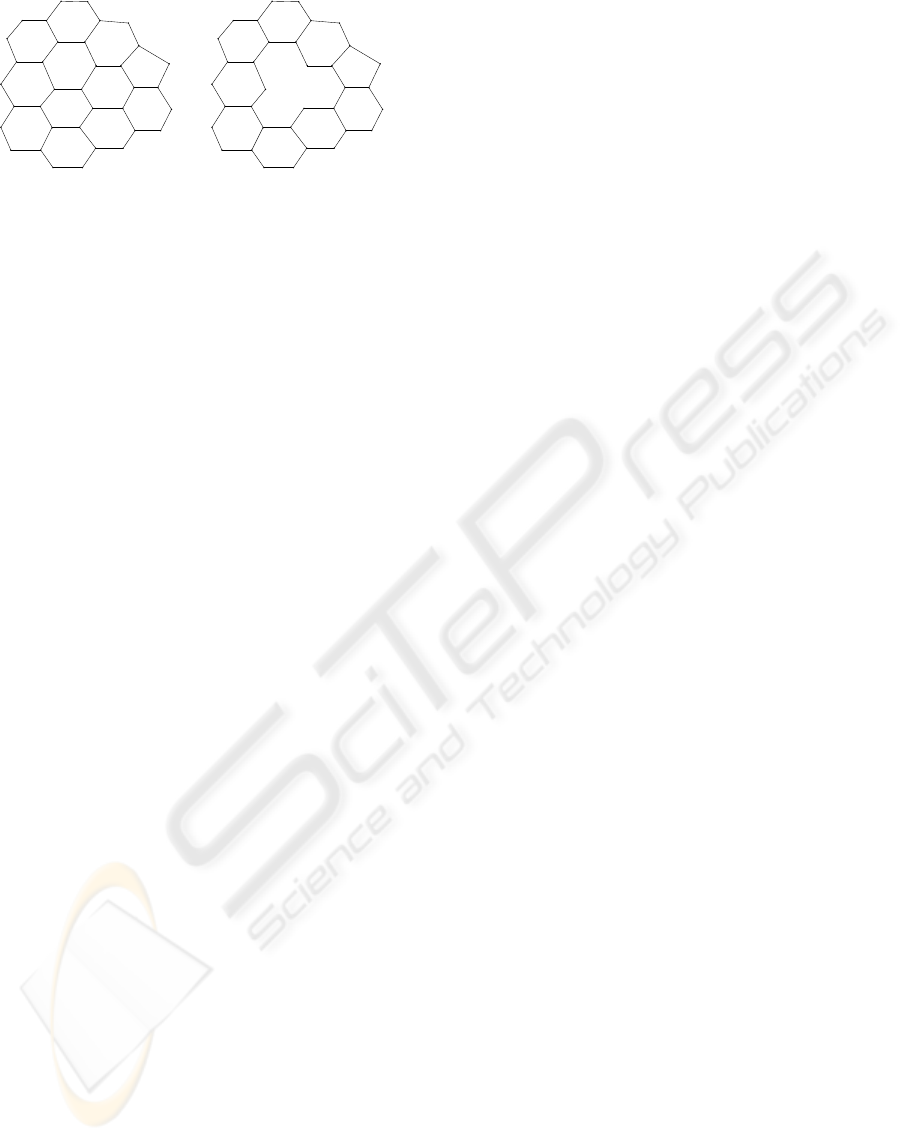
For example, if r = 2, a 1D cycle of k + 3 non-
collinear vertices has rigidity −k, see Figure 4. How-
ever, most rigid cycles are not boundaries of sim-
plices. For example, the boundary of any column or
wedge is a 2D rigid cycle.
A
B
C
D
E F
G
H
I
J K
L
Figure 4: Rigidity of 1D cycles: rigid (left), elastic (middle)
and plastic (right).
Our principle of rigidity is that rigid cycles are al-
ways identified as faces, and elastic cycles are more
likely to be faces than plastic ones. The explanation
is as follows:
1. Rigid cycles are boundaries of either real or interior
faces of the object. If they are all assigned as faces,
they never force any two faces of different planes
to be coplanar. If the object is not assumed to be a
manifold, then taking all rigid cycles as real faces
conforms to the principle of psychological selec-
tion.
If the object is required to be a manifold, then tak-
ing all rigid cycles as real faces induce a decompo-
sition of the object into smaller ones of the same di-
mension, and by our manifold assembly algorithm
to be introduced in the next section, all interior
faces can be removed.
2. Elastic cycles are next to rigid ones in simplicity.
Experiments show that they are the next most plau-
sible face candidates.
3 NEW TECHNIQUES AND
ALGORITHM FOR
COGNITION
Below we propose several new techniques for struc-
tural reconstruction based on the above perception
principles. Without loss of generality, we only de-
scribe the classical case of finding 1D cycles in 2D
face identification.
3.1 Localization
To speed up the finding of the highest dimension, we
propose to search for the cycles locally in the wire-
frame, then propagate the result to construct more cy-
cles. This technique proves to be effective also in re-
ducing the number of redundant cycles.
Let C be a wireframe model. A local wireframe
model of C is a subset of the vertices of C together
with all the higher dimensional faces formed by the
subset of vertices. A localization filter, or localiza-
tion, of C is a sequence of local wireframe models
S
1
⊂ S
2
⊂ . . . ⊂ S
k
= C in which each successor
introduces more vertices than its predecessor. With
the introduction of new vertices, all the edges among
them and the existing vertices are introduced.
Localization is often realized by propagation
through edges. Starting from a vertex called the ori-
gin, we localize the wireframe by considering only
the subgraph of the origin and its neighboring ver-
tices. Within the local wireframe we identify the
faces. Then we set the origin to be the current local
wireframe, and repeat the localization and identifica-
tion procedure. By introducing new vertices accord-
ing to the closeness of their relations with the existing
ones and the rigidity of the cycles formed by them,
the complexity of cycle searching can be reduced.
In Figure 5(a), a localization goes as follows:
{1} ⊂ {1, 2, 3, 4} ⊂ {1, 2, 3, 4, 5, 6, 7, 8, 9, 0}
⊂ {1, 2, 3, 4, 5, 6, 7, 8, 9, 0, a, b, c}.
VISAPP 2006 - IMAGE UNDERSTANDING
72
2
6
b 7
3
1
8
c
94
5
a
0
(a)
2
6
b 7
3
8
c
94
5
a
0
(b)
Figure 5: Localization, deletion and blocking.
3.2 Deletion
To further control the number of face candidates,
we propose two techniques deletion and blocking, to
reduce the scope of cycle searching by deleting or
blocking the branches that do not produce any new
face candidates.
For a general object, the criterion for an edge to be
deletable is that the deletion does not influence the fi-
nal identification of 2D faces and polyfaces. By our
principle of psychological selection, an edge E in the
procedure of localization can be deleted if by assign-
ing any new cycle through it as a face, (1) the num-
ber of non-coplanar faces does not increase, (2) if any
new vertex V is to be added into the polyface con-
taining the face, there is always a cycle of edges in
the polyface that passes through V but not E, i.e.,
deleting E does not prevent V from joining the poly-
face via a cycle of edges. The following theorem can
be proved within graph theory.
Deletion Theorem. In cycle searching, if for an
edge E not collinear with any other edge, all its
neighboring edges are already in faces containing
edge E, then E can be deleted. Such an edge is said
to be saturated.
In Figure 5(a), if three cycles 125a04, 138c94
and 126b73 are already assigned as faces, then edges
12, 13, 14 are saturated and can be deleted. Then ver-
tex 1 is no longer connected to any other vertex and
can be deleted. See Figure 5(b).
3.3 Path Blocking
In Figure 5(b), the vertices in the localization form
a big cycle 25a049c837b6. This cycle cannot be a
face, otherwise all three constructed faces have to
be merged. In searching for more face candidates
passing through a fixed vertex, those faces having
been identified can block off some search branches
by avoiding identified faces to merge, according to
our principle of psychological selection. This tech-
nique is extremely useful in reducing the number of
branches in cycle searching.
For a general object, if a branch of edges intersects
a face at least at three vertices which are not collinear,
then the branch is blocked by the face. The block is
called a face block. If a branch meets two different
face blocks, then it is blocked permanently. If along a
branch there is only one face block, then the branch of
edges can be merged with the face to form a polyface.
In Figure 5(b), suppose we want to find a new cy-
cle passing through vertex 2. From 2 to 6, the path
is blocked by face 62137b. From 2 to 5, the path
is blocked by face 04125a. The two different face
blocks permanently block any new cycle from pass-
ing through branch 625.
In (Liu et al., 2002), the models are 2D manifolds in
which no two neighboring faces are coplanar. If a cy-
cle is identified as a face then no other branch passing
through two edges of it can generate a face. Here one
face suffices to block off the branch permanently. For
a general object, this single blocking does not work.
There are other types of blocks. The 2D non-self-
intersection constraint can block some branches per-
manently. The blocks are called intersection blocks.
The 2D non-interior-intersection constraint can block
some branches from including the interior of an exist-
ing face. The blocks are called interior blocks. The
2D chordless constraint can permanently block some
branches from generating cycles with chords. The
blocks are called chord blocks.
3.4 Manifold Assembly
In many applications it is required that the object be a
2D manifold. For this special purpose, there are two
alternatives to revise our general-purposed structural
reconstruction algorithm:
Anterior Approach: Employ the a priori constraints
of a 2D manifold in the general algorithm from
the start, by revising the localization, deletion and
blocking techniques accordingly (Liu et al., 2002).
Posterior Approach: Use the general algorithm to
produce a set of 3D faces which are themselves 2D
manifolds. Assemble the 3D faces into a single 2D
manifold. This approach, called manifold assem-
bly, appears to be more efficient than the previous
one.
Our manifold assembly algorithm follows a local
propagation approach, and employs the following 2D
manifold assembly principles:
Principle 1. (Face assembly) If two 3D faces inter-
sect at a 2D face whose edges are of degree greater
than two, then the 3D faces can be assembled at the
2D face by removing it; if one edge has degree two,
then one 3D face must be deleted.
Remark: For a set of rD faces, the degree of an
(r − 1)D face with respect to the set is the number
A FAST ALGORITHM FOR ND POLYHEDRAL SCENE PERCEPTION FROM A SINGLE 2D LINE DRAWING
73
1
2
3
4
6
7
8
5
A
B
C
D
H
E
F
G
a
b
c
(a)
A
B
C
D
E
F
G
H
I
J
K
L
N
O
P
Q
R
S
(b)
Figure 6: Manifold assembly principles.
of elements in the set passing through the (r − 1)D
face.
For example, in Figure 1 we can assemble columns
F
1
F
1
′
F
1
′′
and F
1
′′
F
2
′′
F
3
′′
, and denote the result by
O. Then face F
1
′′
is deleted, and its neighbors
F
1
, F
1
′
, F
2
′′
, F
3
′′
each have a degree-2 edge. The
four neighbors disallow the other four columns to be
annexed to O. As a result, vertex V
1
′′
is absent from
O. Although O itself is a 2D manifold, it does not
provide the whole line drawing with such an explana-
tion.
Principle 2. (Edge assembly) If two 3D faces inter-
sect at an edge E but not at any 2D face, then they
can be assembled at the edge if and only if within
the line drawing, a 2D face F
1
at E in one 3D face
is within the 2D region of a 2D face F
2
at E in
the other 3D face. If no such two 2D faces then
one 3D face must be deleted; else the assembling
is realized by replacing the two 2D faces by their
difference in the polyface generated by them.
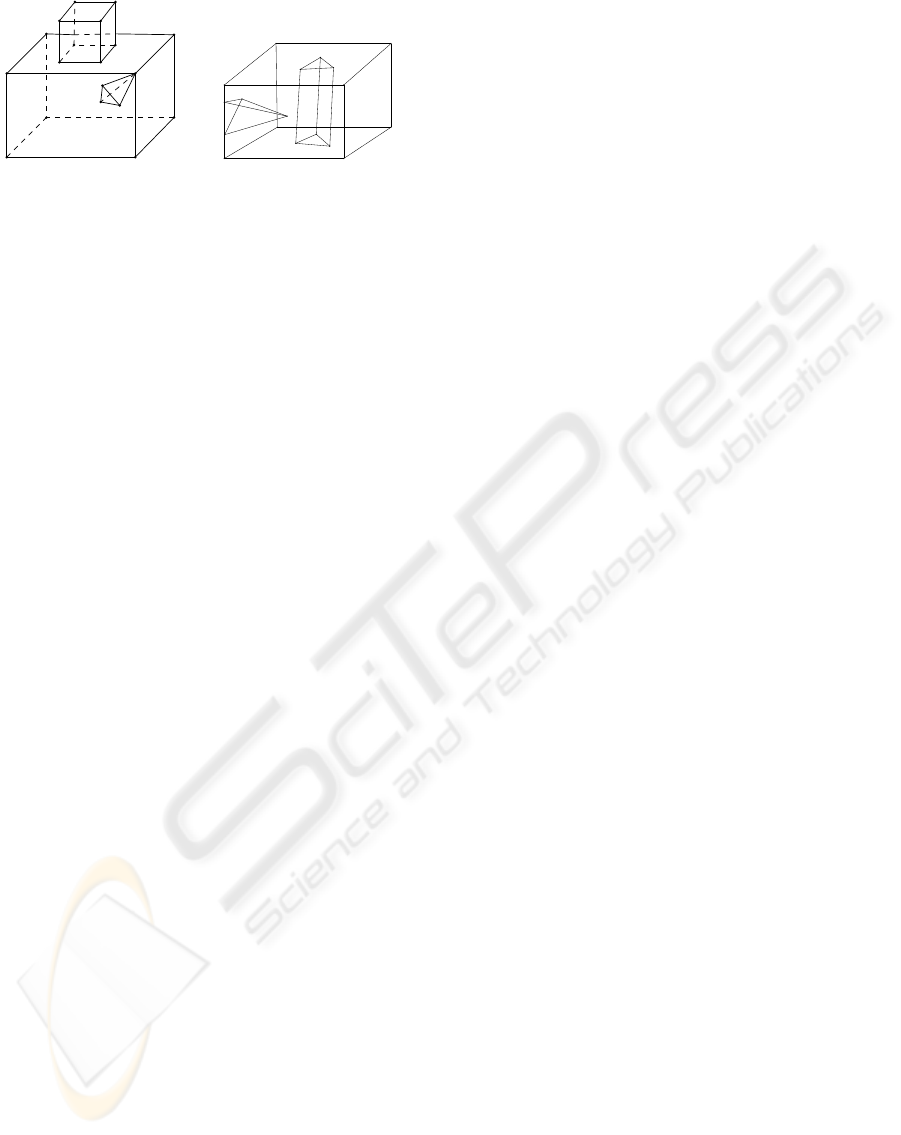
For example, in Figure 6(b) cube ABCDEF GH
and tetrahedron IJ KL share a common edge IJ.
Face IJK can be merged into either face BCEG or
face ABGH. On the other hand, face IJL can only
be merged into face BCEG. As a result, face IJK
can only be merged into face ABGH.
Principle 3. (Vertex assembly) If two 3D faces in-
tersect at a vertex V but not at any 2D face or edge,
then they can be assembled at the vertex if and only
if within the line drawing, a 2D face F
1
at V in
one 3D face is within the 2D region of a 2D face
F
2
at V in the other 3D face. If no such two 2D
faces then one 3D face must be deleted; else the
assembling is realized by replacing the pair of 2D
faces by their difference in the polyface generated
by them.
For example, in Figure 6(a) cube 12345678 and
tetrahedron 3abc intersect at vertex 3. Face 2376 can
be merged with either face 3ab, or face 3ac, or face
3bc, leading to three different manifold structures.
Principle 4. (Empty assembly) If two 3D faces do
not intersect, then they can be assembled at two 2D
faces if and only if one 2D face is within the 2D
region of the other 2D face. To assemble the two
3D faces is to replace the pair of 2D faces by their
difference in the polyface generated by them.
For example, in Figure 6(a) cube 12345678 and
cube ABCDEF GH can be assembled at either the
pair of faces (1234, ABCD), or the pair of faces
(1584, ABCD), leading to two different manifolds.
Principle 5. (Orientation assembly) If two 3D
faces are assembled then their orientations must be
compatible at their common 2D faces.
For example, in Figure 6(b) cube ABCDEF GH
and column NOP QRS can be assembled in four dif-
ferent ways:
(1) (ABCD, N OP ) and (EF GH, QRS),
(2) (ADF H, NOP ) and (EF GH, QRS),
(3) (ABCD, N OP ) and (BCEG, QRS),
(4) (ADF H, NOP ) and (BCEG, QRS).
In assemblings (2) and (3) the orientations of the
cube and the column are incompatible at their com-
mon faces, so only assemblings (1) and (4) are al-
lowed.
3.5 The Main Algorithm – nDView
Input: (1) a 2D line drawing composed of vertices
and edges. A vertex is represented by its 2D coor-
dinates, an edge by two vertices.
(2) A set of lines. A line is represented by a se-
quence of collinear edges.
(3) A vertex as the origin of localization.
Output: Objects of dimension > 1: faces and poly-
faces.
Initialization: Find all pairs of edges intersecting not
at a vertex.
Step 1. Localization start: Start from the origin,
use localization to generate a set of new vertices.
Step 2. Cycle searching: Generate faces by the
depth-first cycle searching strategy, together with
the deletion and blocking techniques.
Step 3. Dimension upgrading: Start from the 2D
local wireframe constructed so far, construct higher
dimensional faces in a hierarchical order, following
a procedure similar to Steps 1 to 3.
Step 4. Assembling: It occurs if the result is re-
quired to be a manifold of given dimension. The
assembling is also local.
Step 5. Localization end: Go back to Step 1 for an-
other round of localization. Terminate after all ver-
tices are included.
Step 6. More solutions and completeness: Explore
the state-space trees to get more (or all) solutions.
The vertices of the rD state-space tree are rD
VISAPP 2006 - IMAGE UNDERSTANDING
74
non-rigid cycles with their states. A vertex here
has two states: either the cycle is identified as a
face, or not allowed to be a face. A descendent
of a vertex in the tree is a cycle found after the
vertex (cycle with a state) has been found in the
localization.
Remark. (1) Although a specific set of 2D co-
ordinates are given in the input, they are used
only to test the inequalities occurring in the 2D
non-self-intersection constraint, the 2D non-interior-
intersection constraint and the 3D assembly. A solu-
tion based on these coordinates is acceptable as long
as the polyhedral structures are compatible, no matter
if the coordinates satisfy the realizability conditions
for nD geometric reconstruction. This is true for all
face identification algorithms in the literature.
(2) The main algorithm above improves the practi-
cal efficiency but not the theoretical one. Step 6 is a
procedure having double exponential complexity for
a fixed dimension r. For the examples tested in our
experiments, the algorithm can always find a solution
reaching the maximal dimension without resorting to
Step 6. if a different solution is needed, then chang-
ing the origin of localization in the imput is usually a
better option than carrying out Step 6.
3.6 Experiments
We have implemented nDView in VC++ 6.0,
have tested all the examples in (Agarwel and
Waggenspack, 1992), (Liu and Lee, 2001), (Liu et al.,
2002), (Shpitalni and Lipson, 1996), etc., in addition
to a dozen higher dimensional ones designed by our-
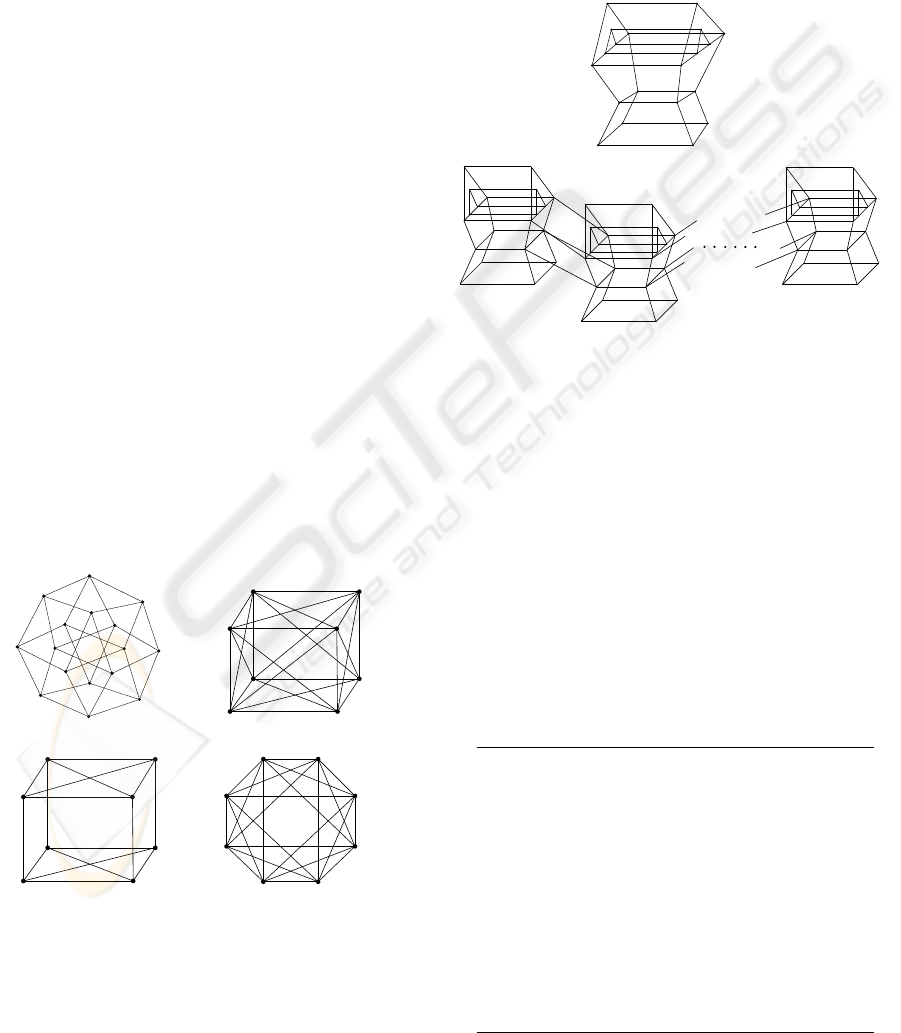
selves, e.g. the line drawings in Figure 7.
(a)
1
2
4
3
6
7
8
5
(b)
1
2
4
3
6
7
8
5
(c)
1
6
2
3
4 7
8
5
(d)
Figure 7: 4D cube (a); 5D polytope (b); 4D polytope (c);
5D polytope (d).
For the classical case m = n = 3, we make com-
parison between our algorithm and the existing fastest
algorithm for face identification of 2D manifolds (Liu
et al., 2002), using the steam box model shown in
Figure 8(a) and a sequence of N steam boxes con-
nected by cubes as typical 2D manifolds of genus N.
The reason for this choice is that Figure 8(a) is the
most complicated example in (Liu et al., 2002) and
about half of the cycles constructed there are redun-
dant ones, in sharp contrast to all other examples in
that paper.
4
1
3
2
5
8
7
6
a b
9
0
c
f
e
d
g
j
h
i
(a)
(b)
Figure 8: Face identification.
The following table collects some data from our ex-
periment. In the table, by “global search” we mean
the algorithm in (Liu et al., 2002), by “local search”
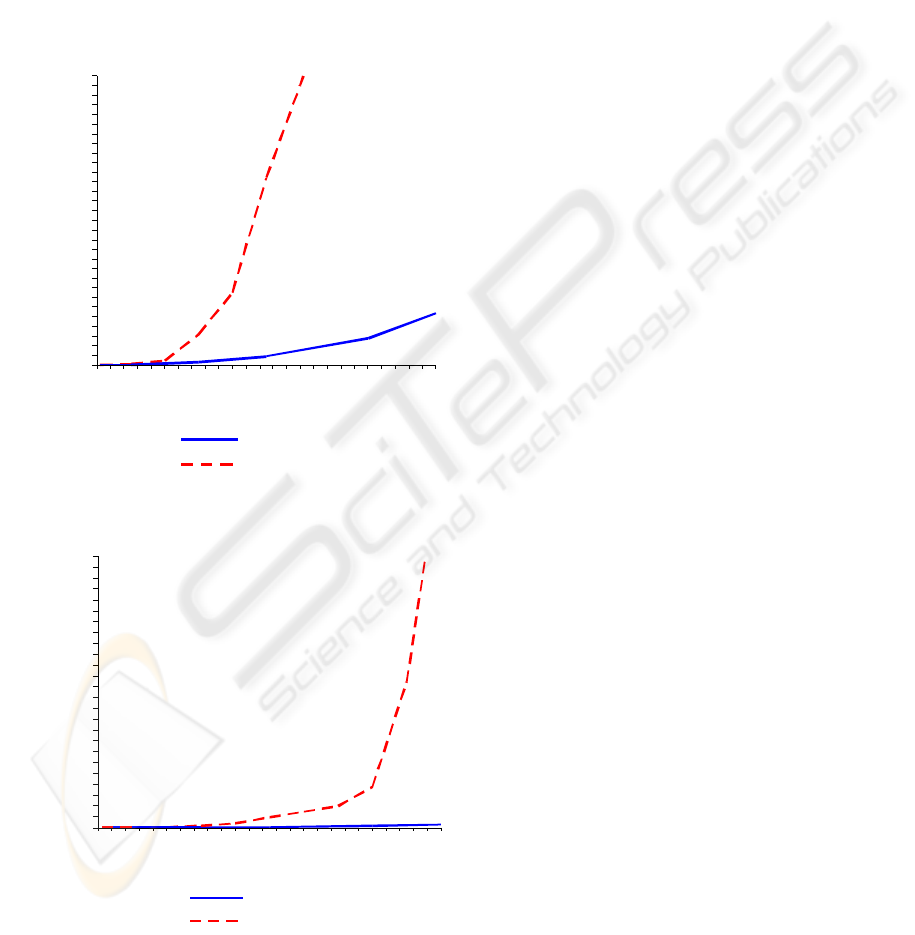
we mean our algorithm nDView. The table reveals
that for very small N our algorithm runs a little bit
slower, but very soon with the growth of N, our algo-
rithm runs much faster. For n = 100 our algorithm
runs more than 100 times faster than the algorithm in
(Liu et al., 2002). Figure 9 in the next page shows the
comparison of the computing time graphically. The
tests are made on an HP Desktop PC of Intel 3.40GHz
CPU and 1GB RAM.
N Global search Local search G : L
time G (sec.) time L (sec.)
1 0.006 0.025 0.24
10 6.172 1.890 3.26
20 23.796 7.094 3.35
30 189.589 16.687 11.36
40 450.031 31.687 14.20
50 1165.547 53.077 21.96
60 1745.013 81.578 21.39
70 2383.511 118.328 20.14
80 4513.983 165.358 27.29
90 16148.985 230.562 70.04
100 41327.325 320.765 128.83
A FAST ALGORITHM FOR ND POLYHEDRAL SCENE PERCEPTION FROM A SINGLE 2D LINE DRAWING
75
4 CONCLUSION
In this paper, we study the problem of machine per-
ception of nD polyhedral scenes from a single 2D line
drawing. We propose a number of efficient techniques
for the structural reconstruction. By testing them with
classical 3D examples, we find their superiority over
existing ones. The work should prove to be valuable
for high-dimensional scientific and artistic visualiza-
tions.
N: number of steam boxes
10080
time
(minutes)
60
30
40
25
20
20
15
0
5
10
0
Local Search
Global Search
N: number of steam boxes
100806040200
time
(minutes)
500
300
400
200
100
0
Local Search
Global Search
Figure 9: Comparison of computing time: local search
(solid line) vs global search (dashed line).
REFERENCES
Agarwel, S. and Waggenspack, C. (1992). Decomposition
method for extracting face topologies from wireframe
models. In Computer Aided Design. 24(3): 123–140.
Courter, S. and Brewer, J. (1986). Automated conversion
of curvilinear wireframe models to surface boundary
models. In Comput. Graph. 20(4): 171–178.
Ganter, M. and Uicker, J. (1983). From wireframe to solid
geometric: Automated conversion of data representa-
tions. In Computer in Mechanical Eng. 2(2): 40–45.
Hanrahan, P. (1982). Creating volume models from edge-
vertex graphs. In Computer Graphics. 16(3): 77–84.
Liu, J. and Lee, Y. (2001). A graph-based method for face
identification from a single 2d line drawing. In IEEE
Trans. on PAMI. 23(10): 1106–1119.
Liu, J., Lee, Y., and Cham, C. (2002). Identifying faces in
a 2d line drawing representing a manifold object. In
IEEE Trans. on PAMI. 24(12): 1579–1593.
Marill, T. (1991). Emulation the human interpretation of
line drawings as 3d objects. In International J. of
Computer Vision. 6(2): 147–161.
Miyazaki, K. (1983). An Adventure in Multidimensional
Space: The Art and Geometry of Polygons, Polyhedra,
and Polytopes. Wileyinterscience Publ.
Shpitalni, M. and Lipson, H. (1996). Identification of faces
in a 2d line drawing projection of a wireframe object.
In IEEE Trans. on PAMI. 18(10): 1000–1012.
VISAPP 2006 - IMAGE UNDERSTANDING
76
