POINT CLOUD DENOISING USING ROBUST PRINCIPAL

COMPONENT ANALYSIS

Esmeide A. Leal Narváez, Nallig Eduardo Leal Narváez

Faculty of Engineering, University of Antioquia, Cl 67 No 53 – 108, Medellín, Colombia

Keywords: Point Cloud Denoising, PCA, Robust Estimation, Shrinkage, Smoothing.

Abstract: This paper presents a new method for filtering noise occurring in point cloud sampled data. The method

smoothes the data set whereas preserves sharp features. We propose a new weighted variant of the principal

component analysis method, which instead of using exponential weighting factors inversely proportional to

the Euclidean distance to the mean, which is computationally expensive, uses weighting factors assignment

by inversely proportional repartition of the sum of distance to the mean. The determination of weighted

factors by means of inverse proportional repartition makes our variant robust to outliers. Additionally, we

propose a simple solution to the problem of data shrinkage produced by the linear local fitting of the

principal component analysis. The proposed method is simple, easy to implement, and effective for noise

filtering.

1 INTRODUCTION

Data filtering is a task of vital importance in areas

like signal processing, statistical analysis, computer

vision and 3D object reconstruction. In these areas

there is a huge information quantity, represented by

discrete samples, which need to be processed for

reducing the noise produced by devices in the

acquisition process. Though 3D reconstruction

applications have been growing due to the

improvements in the 3D scanner technology, there is

a remaining problem: the raw data produced by 3D

scanners are noisy and are far away of being used

directly into the 3D reconstruction process without a

previous processing.

The development of robust point clouds

denoising algorithms has received much attention in

last years. The goal of such algorithms is either to

remove or to reduce the noise in the data, whereas

preserving sharp features on the original surface

model. So far, researches in the field of digital image

filtering have been adapted for point clouds filtering

algorithms. Nevertheless, the adaptation of

algorithms for digital image filtering to point clouds

filtering is not direct, due to three main reasons:

irregularity, shrinkage, and drifting. The irregularity

refers to the irregular sampling density of the point

clouds. The shrinkage and the drifting refer to the

volume reduction and the spatial displacement

suffered by the points, which are produced by the

use of the mean instead of the data points

(Fleishman, 2003).

Principal Component Analysis (PCA), initially

used for digital image processing, has been adapted

for point clouds processing (Gumhold, 2001, Pauly,

2002). This adaptation has a drawback: PCA is

highly sensitive to the outliers present in the point

clouds. There are several variants that fix this

drawback (Rousseeuw, 1999, De la Torre, 2001,

Skokal, 2002, Hubert, 2005), almost all of them are

based on robust statistics (Huber, 1981). Such

variants, called robust or weighted PCA, improve

the PCA, making it less sensitive to the outliers.

However, the robust PCA variants use exponential

weighting factors to correct the outlier problem,

which is computationally expensive.

This paper presents a new method for point

clouds denoising. Our method first calculates a

weighted mean. The weighting factors assignment of

the mean is achieved by inversely proportional

distributing the sum of distances to the mean. Then,

using the weighting factors and the mean, the

method constructs a covariance matrix and realizes

an eigen-analysis of such matrix. In this way it is

obtained a fitting plane expanded by the

eigenvectors corresponding to the largest

eigenvalues, and a normal vector to the plane, which

A. Leal Narváez E. and Eduardo Leal Narváez N. (2006).

POINT CLOUD DENOISING USING ROBUST PRINCIPAL COMPONENT ANALYSIS.

In Proceedings of the First International Conference on Computer Graphics Theory and Applications, pages 51-58

DOI: 10.5220/0001358900510058

 SciTePress

is oriented in the direction of the third eigenvector

corresponding to the smallest eigenvalue. Then, a

displacement of the neighbourhood mean along the

normal vector is achieved in order to preserve sharp

features.

The main contributions of this work are: i) a

simple method for point clouds denoising that does

not require a either previous mesh representation,

nor local polynomial fitting, ii) a simple approach to

prevent the shrinkage problem, and iii) a mechanism

for bias reduction. Our method is robust to outliers,

fast and easy to implement.

The remainder of this paper is organized as

follows. In section 2, related work dealing with

mesh and point clouds denoising algorithms are

presented. In section 3, a short review of principal

component analysis is presented. In section 4, the

stages of our method are explained. In section 5, the

results of our method are shown. In section 6,

conclusions and future work are discussed.

2 RELATED WORK

Point clouds have become a primitive for surface

representation and geometric modelling; however

such point clouds are noisy due to the inherent noise

of the acquisition devices. Point clouds should be

noise free for using in 3D reconstruction. Recently, a

great research effort has been done in mesh and

point clouds denoising and smoothing, producing

numerous algorithms.

Taubin (Taubin, 1995) applies in mesh

smooting a discrete version of the Laplacian

Operator, which is taken from signal processing. The

method is linear in both time and memory.

Desbrum et al. (Desbrum, 1999, Desbrum,

2000) and Bajaj (Bajaj, 2003) successfully use

anisotropic diffusion over meshes, in order to

improve the smoothing in reasonable time.

Peng et al. (Peng, 2001) use locally adaptive

Wiener filtering for denoising geometric data

represented as semiregular mesh. The algorithm

allows interactive local denoising.

Pauly and Gross (Pauly, 2001) apply Wiener

filtering to restore surfaces from point clouds in

presence of blur and noise.

Fleishman et al. (Fleishman, 2003) and Jones et

al. (Jones, 2003) have independently proposed the

use of Bilateral filtering based on robust statistics for

features preserving and mesh smoothing.

Mederos et al. (Mederos, 2003) follows the

same approach that Fleishman and Jones, by

modifying a high order fitting method, called

Moving Least Squares (MLS), to preserve sharp

features. Their approach also considers optimization

techniques for reducing the execution time of the

algorithm.

Choudhury and Tumblin, (Choudhury, 2003)

present a single-pass nonlinear filter for edge

preserving and smoothing. The method is called

Trilateral filtering and it is an evolution of the

Bilateral filtering. The filter produces better outlier

rejection and strong noise reduction than Bilateral

filtering.

Schall et al. (Schall, 2005) have proposed a

probabilistic method which consists of using a

kernel density estimation technique. It associates to

each point a local measure of probability to locate

the point into the surface. The method achieves

effectiveness result in filtering and robustness in

outliers detection.

3 PRINCIPAL COMPONENT

ANALYSIS

Principal Component Analysis (PCA) is a statistical

method that tries to explain the covariance structure

of data by means of various components expressed

as linear combinations of the original variables

(Hubert, 2005).

The first component of PCA corresponds to the

direction in which the projected data have the largest

variance. The second component is orthogonal to the

first component, and maximizes the variance of the

data points projected on it.

PCA is applied widely in bias identification into

data sets. It is used for data dimensionality reduction

and visualization (Jolliffe, 1986), data clustering

(Pauly, 2002) and pattern recognition (De la Torre,

2001). Despite the versatility of PCA, it is sensitive

to outliers present in data. Figure 1a shows a set of

points mainly concentrated at the low part of the

figure. Three of them, which are considered outliers,

are enclosed in red circles. The first component of

PCA, blue line, should indicate the main direction of

data dispersion, but it is observed a bias produced by

the outliers. Figure 1b shows the correction by

robust PCA.

The PCA, first take a set of neighbors

)(

around a point

, next the neigborhood mean

is

estimated using (1). Finally, using (2), the

covariance matrix

is obtained from the points

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

(a) (b)

Figure 1: Principal components of a dataset. (a) PCA (b)

Robust PCA.

and the neigborhood mean.

∑

)(

pNp ∈

(1)

∑

−−=

pppp

))((

(2)

It is observed that CM is a symmetric positive semi-

definite 3x3 matrix. The CM eigen-decomposition

produce the principal components with their

associated three eigenvectors

321

,, vvv

 and three

real eigenvalues

321

≤≤

. The eigenvalues

measure the variation of the points in the

neighborhood along of the directions of their

corresponding eigenvectors. The orthogonal

eigenvectors

,vv

define the directions of highest

variation and expand a fitting plane on the

neighborhood. The eigenvector

approximates the

normal vector

at

.

4 PROPOSED METHOD

The method has four stages: weights assignment for

the PCA by inversely proportional repartition,

features preservation, shrinkage prevention and bias

correction.

Starting from a noisy point set

}{

RpP

∈=

,

close to an unknown and smooth two dimensional

manifold boundary surface S, we want to determine

a noise free point set P’ that preserves the sharp

features of the surface from which they were

sampled. The main idea is to use a robust version of

PCA, which allows determining a local fitting plane

to a neighbourhood

)(

, close enough to the

surface S. Such fitting plane is not influenced by the

outliers due to the weights assignment by inversely

proportional repartition. In addition, the PCA

establish an orthogonal unit vector to the plane in the

point

, which is an estimation of the true normal at

. Once we have the normal vector and the fitting

plane, we apply the operator

tnpp +='

(Alexa,

2001, Fleishman, 2003) to preserve sharp features of

S. Then, our method prevents the shrinkage and the

drifting by shifting the neigborhood mean projection

along the tangent plane. The bias produced by the

linear approximation of PCA is reduced by applying

the bootstrap method.

4.1 PCA and Inverse Repartition

The weights assignment by inversely proportional

repartition is the key of the robustness of our robust

PCA variant. The weights assignment is done

according to (3). In that way, we punish with small

weights the points farthest respect to the mean and

we recompense with large weights the points near to

the mean. Using inversely proportional repartition,

the outliers influence over the mean is reduced and

the principal components are not biased by them.

This weights estimation is neither computationally

expensive nor dependent of user parameters.

⎪

⎩

⎪

⎨

⎧

⋅

∑

cases other in ,

jmeani

pNDd

))((

(3)

In (3)

∑

))((

jmean

pND is the sum of the

distances between the points in the neighborhood of

(including

) and the neighborhood mean,

is the Euclidian distance between the neighborhood

mean and a point

in the neighborhood. To

estimate the weighted mean

, robust to outliers,

we use (4). The weights are estimated for each point

)(

, and we use this weights and the

weighted mean to compute the weighted covariance

matrix, using (5).

∑

(4)

Wpppp

wiwiw

∑

−−=

))((

(5)

POINT CLOUD DENOISING USING ROBUST PRINCIPAL COMPONENT ANALYSIS

where CM

is the weighted covariance matrix,

{

}

wwW ,...,

, are the weighs associated to

each point



)(

pNp ∈

.

Once we have already estimated the covariance

matrix, its eigen-analysis produces a robust PCA.

Figure 1b, shows the correction of the problem using

our PCA variant, including the inverse repartition.

These variations let our algorithm detect outliers and

made it robust to noise.

4.2 Features Preservation

To prevent over smoothing of the point cloud and, in

consequence, the lost of sharp features, we apply a

shift to the mean along of the normal direction. We

obtain the new position of the mean using (6).

pmw

ntpp

(6)

where

, is the new position of the mean,

is the

original weighted mean estimated by (4),

is the

normal approximation to the plane at

, given by

the robust PCA, and

is the displacement

calculated by (7).

∑

∈

−=

)(

pNp

ipm

ppnmeant

(7)

The above quantity, under the constraint

, is taken as the minimal height needed for

displacing the mean along of the normal direction.

4.3 Shrinkage Prevention

Linear fitting algorithms are based on the mean of

the neighborhood around a point

, this produce

data shrinkage, because these algorithms use the

neighborhood centroid

(free of noise) instead of

the original point

. We correct this problem by

applying a shift to the centroid

, in the direction

of the projection of the vector

'pp −

onto the

tangent plane to the neighborhood. The centroid

is on the tangent plane and

is on the point cloud,

as it is shown Figure 2.

Figure 2: Data shrinkage prevention.

The new centroid

dis

is calculated using (8).

'' pOrthop

dis

(8)

TTppOrtho ),( −=

(9)

where Ortho, is the orthogonal projection of the

vector

'pp −

onto the neighbourhood tangent plane

T in

, and

⋅

is the dot product operator. Figure

3a shows data points sampled from a synthetic curve

(blue dots) and its corresponding noisy data (red

dots). Figure 3b shows the smoothed noisy data

without shrinkage prevention (green dots) and

Figure 3c shows the correction of the shrinkage

problem after applying (8). It is important to note

that for a correct application of (8), the surface must

be sufficiently sampled in regions with high

curvatures.

4.4 Bias Correction

An additional problem introduced by the linear

fitting is the bias between the original point and the

neighborhood mean. We correct this problem using

bootstrap bias correction (Martinez, 2002). We first

perform a pass using our PCA variant; then, we

perform a second pass including the bootstrap bias

correction according to (10). Figure 4 shows the bias

problem and its correction. Figure 4a shows data

points sampled from a synthetic curve (blue dots)

and its corresponding noisy data (red dots). Figure

4b shows the smoothed noisy data with bias (green

dots) and Figure 4c shows the bias reduction (the

green dots are closer to the blue dots) after the

application of the bootstrap. The bootstrap is an

iterative method, but in our experimental test, a

single iteration was sufficient.

−= pp biasCorr

(10)

where

∑

, is the new neighborhood

mean after the second pass.

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

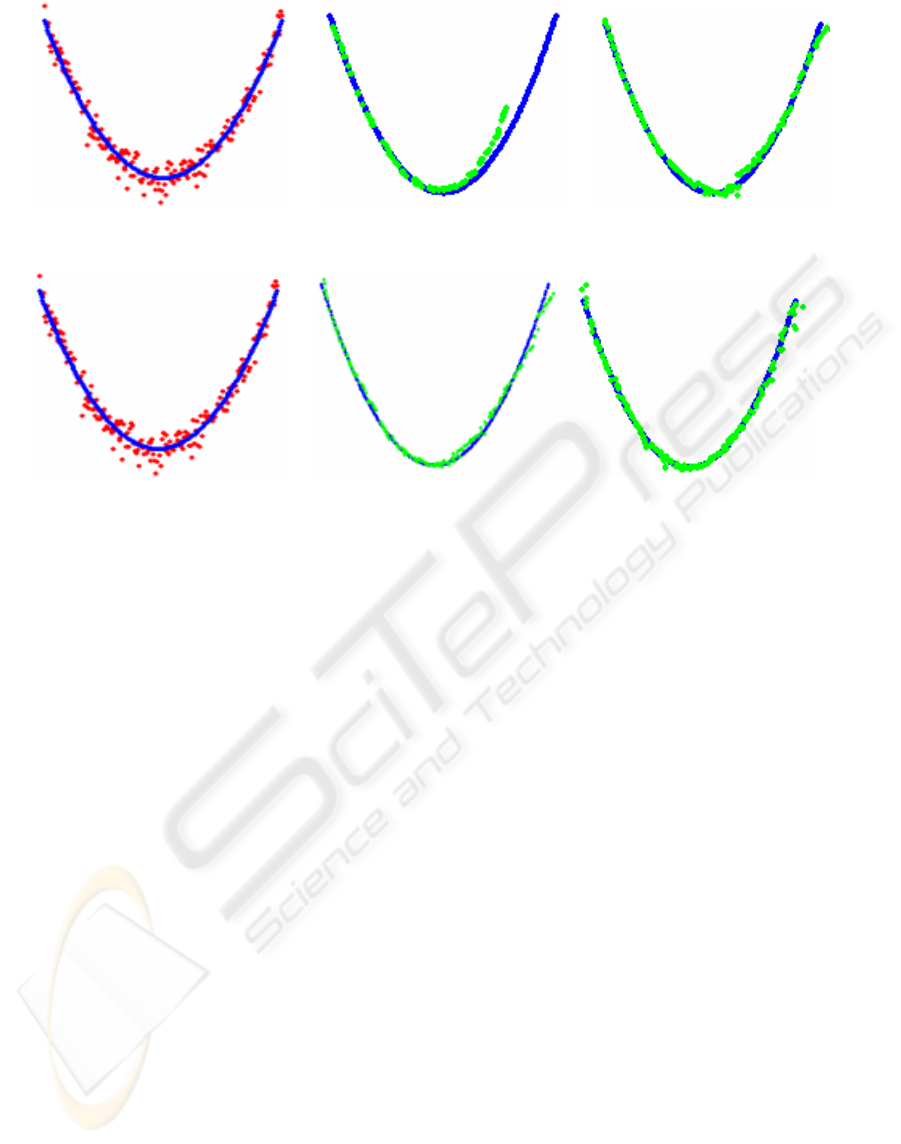
(a) (b) (c)

Figure 3: Shrinkage problem. (a) Noisy data represented by red dots (b) Smoothed data with shrinkage problem, represented

by green dots (c) Smoothed data with shrinkage prevention using (8).

(a) (b) (c)

Figure 4: Bias correction (a) Noisy data represented by red dots (b) Smoothed data with bias problem, represented by green

dots (c) Smoothed data with bias reduction prevention using (10).

5 ANALYSIS AND RESULTS

The proposed method has been tested in 2D and 3D

data sets. The tests were run on a 1.5 GHz Athlon

AMD, with 512 MB of RAM. The result shows that

our algorithm has a good behaviour with different

noise levels. Figure 3, used to illustrate the

shrinkage problem correction, shows a synthetic data

set corrupted with Gaussian noise (

= 1% of the

average spacing between the points). The points

were sampled from a parabola in the interval [-1, 1].

We observe how the algorithm controls the data

shrinkage by applying (8), as shows Figure 3c (green

points), in contrast with shown in Figure 3b, where

the shrinkage prevention has not been applied (green

points). The data shrinkage problem is more evident

at the extremes. In our tests, the proposed method

for preventing the shrinkage problem allowed to

reduce the relative error, between the real and the

approximated volume, from 34% to 10%.

The parabola data set (Figure 4) is also used to

illustrate de bias problem. In one hand we observe

the bias between the data points mean (green dots)

and the original data points (blue dots). In the other

hand, we observe in Figure 4c, the result of applying

the bootstrap bias correction (green dots are closer to

the blue dots). In our tests, after applying (10) the

bias reduction reaches a 57%, i.e. the distance

between the real data points and the smoothed data

points after applying the bootstrap technique was

reduced until a 43% of the initial distance.

The data sets used to illustrate the result of our

method for point cloud denoising were corrupted

with Gaussian noise (zero mean and variance

)

along of the normal direction. We specified the noise

magnitude as a percentage of the average z

coordinate or the diagonal of the bounding box of

the point cloud.

Figure 5 shows a cube model corrupted with

Gaussian noise (

= 5% of z coordinate average).

We observe how our algorithm preserves sharp

features (corners and edges) while smoothes the

point cloud.

In Figures 6 the Max Planck model (50k points)

corrupted with Gaussian noise (

= 0.08% of

diagonal of the bounding box) is shown. The model

was smoothed in 13 seconds. Figures 7 and 8 show

the Venus model (70k points) corrupted with

Gaussian noise (

= 0.05% and

= 0.025% of the

diagonal of the bounding box respectively). The

model was smoothed in 19 seconds. In Figure 9 a

bird model was corrupted with Gaussian noise (

0.1% of z coordinate average) to illustrate the model

detail before and after applying our algorithm. It is

observed the effectiveness of the method eliminating

the noise and preserving the features.

POINT CLOUD DENOISING USING ROBUST PRINCIPAL COMPONENT ANALYSIS

(a) (b) (c)

Figure 5: Sharp features preservation. (a) Original cube model (b) Cube model corrupted model with Gaussian noise (c)

Corrupted cube model after filtering.

(a) (b) (c)

Figure 6: Max Planck model. (a) Original Max Planck model. (b) Max Planck model corrupted with Gaussian noise (c)

Corrupted Max Planck model after filtering.

(a) (b) (c)

Figure 7: Venus model left view. (a) Original Venus model. (b) Venus model corrupted with Gaussian noise (c) Corrupted

Venus model after filtering.

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

(a) (b) (c)

Figure 8: Venus model right view. (a) Original Venus model. (b) Venus model corrupted with Gaussian noise (c) Corrupted

Venus model after filtering.

(a) (b)

Figure 9: Bird model. (a) Bird model corrupted with Gaussian noise (b) Corrupted bird model after filtering.

6 CONCLUSION AND FUTURE

WORK

In this paper we have presented a new and robust

method for point clouds denoising. The method is a

PCA variant that preserves sharp features of the

original surface. In contrast with previous work, our

method does not require high order local fitting

algorithms (like MLS), or global approximation to

surface (like triangular meshes or graphs). The

proposed method operates directly on the points and

does not require neither nonlinear optimization

algorithms nor parameters provided by users. The

method is computationally efficient and easy to

implement.

There is a way to improve our method using an

adaptive neighborhood size instead fixed size. The

neighborhood size should depend on the local

characteristics like curvature and density, this will

allow a better normal estimation and, in

consequence, would improve the application of the

operator

tnpp

. Taking into account the local

curvature, we can reduce the bias between the

neighborhood mean and the data point, in this way,

we are closer to the point of the original surface.

REFERENCES

Alexa, M., Behr, J., Cohen-Or, D., Fleishman, S., Levin,

D., and Silva, C.T., 2001. Point set surfaces. In

Proceedings of the Conference on Visualization, pages

21-28. IEEE Computer Society.

POINT CLOUD DENOISING USING ROBUST PRINCIPAL COMPONENT ANALYSIS

Bajaj, C., L., and XU, G. 2003. Anisotropic diffusion of

subdivision surfaces and functions on surfaces. ACM

Transactions on Graphics (TOG) 22, 1, 4–32.

Choudhury, P., and Tumblin, J., 2003. The Trilateral Filter

for High Contrast Images and Meshes. Eurographics

Symposium on Rendering, pp. 1.11

De la Torre, F., and Black, M.J., 2001. Robust principal

component analysis for computer vision. In ICCV’01,

I: 362–369.

Desbrun, M., Meyer, M., Schroder, P., and Barr, A. H.

1999. Implicit Fairing of Irregular Meshes Using

Diffusion and Curvature Flow. In Proceedings of

SIGGRAPH, 317–324.

Desbrun, M., Meyer, M., Schroder, P., and Barr, A. H.

2000. Anisotropic Feature-Preserving Denoising of

Height fields and Bivariate Data. In Graphics

Interface, 145–152.

Fleishman, S., Drori, I., and Cohen-Or, D., 2003. Bilateral

mesh denoising. ACM Transactions on Graphics

(TOG), 22(3):950-953.

Gumhold, S., Wang, X., and MacLeod, R., 2001. Feature

extraction from point clouds. In 10th International

Meshing Roundtable, Sandia National Laboratories,

pages 293-305, October.

Huber, P. J., 1981. Robust Statistics. John Wiley and Sons.

Hubert, M., Rousseuw, P.J., and Branden, K.V., 2005.

ROBPCA: A New Approach to Robust Principal

Component. Analysis.Technometrics, February, VOL.

47, NO. 1.

Jolliffe, I., 1986. Principal Component Analysis. New

York:Springer-Verlag.

Jones, T. R., Durand, F., and Desbrun, M., 2003. Non-

iterative, feature-preserving mesh smoothing. ACM

Transactions on Graphics (TOG), 22(3):943-949.

Martinez, W.L., and Martinez, A.R., 2002. Computational

statistics handbook with Matlab. Chapman &

Hall/CRC.

Mederos, B., Velho L., and De Figueiredo L. H., 2003.

Robust smoothing of noisy point clouds. In Proc.

SIAM Conference on Geometric Design and

Computing (Seattle, USA), Nashboro Press.

Pauly, M., Gross, M., and Kobbelt, L., 2002. Efficient

simplification of point-sampled surfaces. IEEE

Vizualization, pp. 163–170.

Pauly, M., and M. Gross., 2001. Spectral processing of

point-sampled geometry. Proc. ACM SIGGRAPH, pp.

279–386.

Peng, J., Strela, V., and Zorin, D. 2001. A Simple

Algorithm for Surface Denoising. In Proceedings of

IEEE Visualization, 107–112.

Rousseeuw, P. J., and Driessen, K.V., 1999. A Fast

Algorithm for the Minimum Covariance Determinant

Estimator. Technometrics, 41, 212–223.

Skocal, D., and Leonardis, A., 2002. Weighted

Incremental Subspace Learning. Proceedings of

Workshop on Cognitive Vision. Zurich, Sep.

Schall, O., Belyaev, A., and Seidel, H., 2005. Robust

Filtering of Noisy Scattered Point Data. Eurographics

Symposium on Point-Based Graphics.

Taubin, G., 1995. A Signal Processing Approach to Fair

Surface Design. In Proceedings of SIGGRAPH, 351–

358.

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS