MESH RETRIEVAL BY COMPONENTS
Ayellet Tal
∗
Department of Electrical Engineering
Technion
Emanuel Zuckerberger
Department of Electrical Engineering
Technion
Keywords:
3D shape retrieval, 3D shape matching.
Abstract:
This paper examines the application of the human vision theories of Marr and Biederman to the retrieval of
three-dimensional objects. The key idea is to represent an object by an attributed graph that consists of the
object’s meaningful components as nodes, where each node is fit to a basic shape. A system that realizes this
approach was built and tested on a database of about 400 objects and achieves promising results. It is shown
that this representation of 3D objects is very compact. Moreover, it gives rise to a retrieval algorithm that is
invariant to non-rigid transformations and does not require normalization.
1 INTRODUCTION
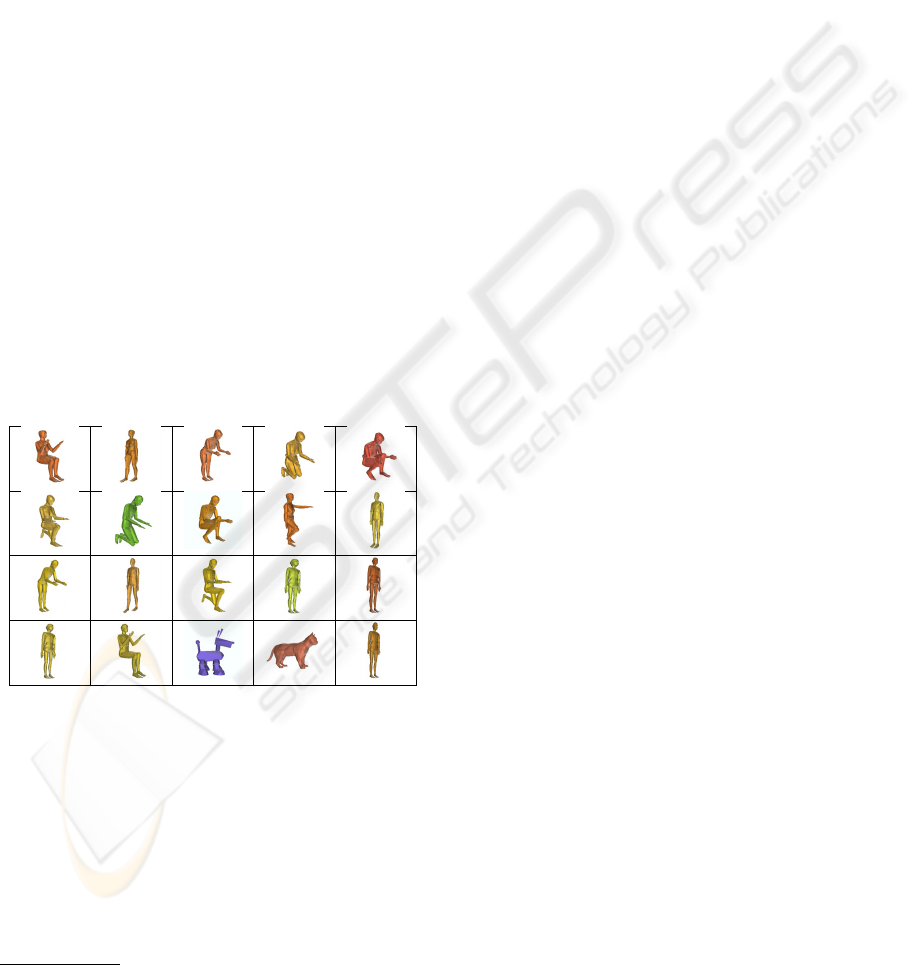
Figure 1: Retrieval of the top 20 objects similar to to the top
left-most human figure.
In his seminal work (Marr, 1982), Marr claims
that the human brain constructs a 3D viewpoint-
independent model of the image seen. This model
consists of objects and spatial inter-relations between
them. Every 3D object is segmented into primitives,
which can be well approximated by a few simple
shapes. Biederman’s Recognition-By-Components
(RBC) theory (Biederman, 1987; Biederman, 1988)
∗
This work was partially supported by European FP6
NoE grant 506766 (AIM@SHAPE) and by the Smoler Re-
search Funds.
claims that the human visual system tends to segment
complex objects at regions of deep concavities into
simple basic shapes, geons. The simple attributed
shapes along with the relations between them form
a stable 3D mental representation of an object.
The current paper proposes a retrieval approach
that attempts to succeed these theories. The key idea
is to decompose each object into its “meaningful”
components at the object’s deep concavities, and to
match each component to a basic shape. After de-
termining the relations between these components,
an attributed graph that represents the decomposition
is constructed and considered the object’s signature.
Given a database of signatures and one specific signa-
ture, the latter is compared to other signatures in the
database, and the most similar objects are retrieved.
Retrieving 3D objects has become a lively topic of
research in recent years (Veltkamp, 2001). A common
practice is to represent each object by a few prop-
erties – a signature – and base the retrieval on the
similarity of the signatures. Some signatures consist
of local properties of the shapes such as histograms
of colors and normals (Paquet et al., 2000), probabil-
ity shape distributions (Osada et al., 2001), reflective
symmetry (Kazhdan et al., 2003a), spherical harmon-
ics (Vranic and Saupe, 2002; Kazhdan et al., 2003b)
and more. Other papers consider global properties,
such as shape moments (Elad et al., 2001) or sphere
projection (Leifman et al., 2005). In these cases, the
objects need to be normalized ahead of time.
142
Tal A. and Zuckerberger E. (2006).
MESH RETRIEVAL BY COMPONENTS.
In Proceedings of the First International Conference on Computer Graphics Theory and Applications, pages 142-149
DOI: 10.5220/0001352001420149
Copyright
c
SciTePress

Our global approach is mostly related to graph-
based algorithms. The Reeb graph is a skeleton deter-
mined using a scalar function, which is chosen in this
case to be the geodesic distance (Hilaga et al., 2001).
In (Sundar et al., 2003; Cornea et al., 2005), it is pro-
posed to represent an object by its skeleton and an
algorithm for comparing shock graphs is presented.
Our approach succeeds these methods, yet differs in
several ways. First, the graphs are constructed differ-
ently, focusing on segmentation at deep concavities,
following (Marr, 1982; Biederman, 1995). Second,
each node and edge in the graph is associated with
properties, resulting in an attributed graph. Third, a
different graph matching procedure is utilized.
Our proposed signature has a few important proper-
ties. First, it is invariant to non-rigid-transformations.
For instance, given a human object, we expect its sig-
nature to be similar to signatures of other humans,
whether they bend, fold their legs or point forward,
as illustrated in Figure 1. In this figure, all the 19
humans in a database consisting of 388 objects, were
ranked among the top 21 objects, and 17 among the
top 17. Invariance to non-rigid-transformations is
hard to achieve when only geometry is considered.
Second, normalization is not required, since the
signature is a graph that is invariant to rigid transfor-
mations.
Third, the signature tolerates degenerated meshes
and noise. This is so because the object is represented
by its general structure, ignoring small features.
Finally, the proposed signature is very compact.
Thus, signatures can be easily stored and transfered.
The remaining of the paper is structured as follows.
Section 2 outlines our approach. Sections 3–4 address
the main issues involved in the construction of a sig-
natures. In particular, Section 3 discusses mesh de-
composition into meaningful components while Sec-
tion 4 describes the determination of basic shapes.
Section 5 presents our experimental results. Section 6
concludes the paper.
2 SYSTEM OVERVIEW
Given a database of meshes in a standard represen-
tation consisting of vertices and faces (e.g., VRML)
and one specific object O, the goal is to retrieve from
the database objects similar to O.
This section starts by outlining the signature com-
putation technique. This is the main contribution of
the paper and thus the next sections elaborate on the
steps involved. Then, the section briefly describes the
graph matching algorithm used during retrieval.
S
IGNATURE COMPUTATION: Let S be an orientable
mesh.
Definition 2.1 Decomposition: S
1
,S
2
,...S
k
is a de-
composition of S iff (i) ∀i,1 ≤ i ≤ k, S
i
⊆ S, (ii) ∀i, S
i
is connected, (iii) ∀i = j,1 ≤ i, j ≤ k, S
i
and S
j
are
face-wise disjoint and (iv) ∪
k
i=1
S
i
= S.
Definition 2.2 Decomposition graph: Given a de-
composition S
1
,S
2
,···S
k
of a mesh S, a graph G(V,E)
is its corresponding decomposition graph iff each
component S
i
is represented by a node v
i
∈ V and
there is an arc between two nodes in the graph iff the
two corresponding components share an edge in S.
Definition 2.3 Attributed decomposition
graph: Given a decomposition graph G(V, E),
G =(V,E,
µ
,
ν
) is an attributed decomposition graph
if
µ
is a function which assigns attributes to nodes
and
ν
is a function which assigns attributes to arcs.
For each object in the database, its attributed de-
composition graph, the object’s signature, is com-
puted and stored. Signature computation is done in
three steps. First, the object is decomposed into a
small number of meaningful components. Second,
a decomposition graph is constructed. Third, each
node and arc of the decomposition graph is given
attributes, following (Biederman, 1987; Biederman,
1988). Specifically, each component is classified as
a basic shape: a spherical surface, a cylindrical sur-
face, a cone surface or a planar surface. The corre-
sponding graph node is given the appropriate shape
attribute. Each graph arc is attributed by the relative
surface area of its endpoint components (i.e., greater,
smaller, equal). We elaborate on signature construc-
tion in the next couple of sections.
R
ETRIEVAL: Given a specific object by the user, the
goal of the system is to retrieve from the database the
most similar objects to this object.
This step requires the comparison of graphs. Graph
matching and subgraph isomorphism has been ap-
plied to many problems in computer vision and pat-
tern recognition e.g., (Rocha and Pavlidis, 1994;
Wang et al., 1997; Lee et al., 1990; Pearce et al., 1994;
Wong, 1992). In the current paper, we follow (Mess-
mer, 1995), which uses error-correcting subgraph iso-
morphism.
The key idea of error correction algorithm is as fol-
lows. A graph edit operation is defined for each pos-
sible error type. Possible operations are deletion, in-
sertion and substitution (i.e., changing attributes) of
nodes and arcs. A cost function is associated with
each type of edit operation. Given a couple graphs,
the algorithm aims at finding a sequence of edit op-
erations with a minimal cost, such that applying the
sequence to one graph results in a subgraph isomor-
phism with the other.
Formally, the algorithm is given two graphs, G =
(V, E,
µ
,
ν
) and G
=(V
,E
,
µ
,
ν
), where V (V
)is
the set of nodes of G (G
), E (E
) is its set of arcs,
MESH RETRIEVAL BY COMPONENTS
143

µ
(
µ
) is a function which assigns attributes to nodes
and
ν
(
ν
) is a function which assigns attributes to
arcs. It is also given a set of graph edit operations
and their corresponding cost functions. The goal is
to find the optimal error-correcting subgraph isomor-
phism (∆,g), where ∆ is a sequence of edit operations
and g is an isomorphism, such that there is a subgraph
isomorphism g from ∆(G) to G
and the cost C(∆) of
∆ is minimal.
The algorithm maintains a search tree. The root
of the search tree contains an empty mapping and is
associated with cost 0. At the next level of the search
tree, the first node of G is mapped onto nodes in G
.
Each such mapping, along with its corresponding cost
of the relevant edit operation, is a node in the search
tree. The generation of the next nodes is guided by the
cost of the edit operations. The node representing the
mapping with the lowest cost in the current search tree
is explored by mapping a new node of G onto every
node of G
that has not yet been used in the path and
the corresponding costs are calculated.
When the first mapping
γ
describing a complete
subgraph isomorphism from G to G
is found, a
threshold parameter is set to the cost C(
γ
) of
γ
.A
node having a cost greater than the threshold is never
explored. Other nodes are explored until a mapping
with the minimal cost is found.
This procedure is applied to the graph representing
the query object against each graph in the database. It
returns a corresponding error value for each pair. The
lower the error, the less edit operations are required
(or the “cheaper” these operations are), and thus the
more similar the objects are. The objects are therefore
retrieved in an ascending order of their error values.
3 MESH DECOMPOSITION
The first step in signature construction is mesh de-
composition into its meaningful components. In re-
cent years, there have been several papers addressing
this problem, e.g. (Katz and Tal, 2003; Li et al., 2001;
Lee et al., 2005; Shamir, 2004; Katz et al., 2005).
These techniques produce very nice decompositions.
However, we will show below that simpler, linear al-
gorithms are sufficient for retrieval.
Our approach follows Biederman’s observation that
“the human visual system tends to segment complex
objects at regions of deep concavities into simple ba-
sic shapes”. Thus, algorithms that generate rough de-
compositions at deep concavities are used.
In (Chazelle et al., 1997), a sub-mesh is called con-
vex if it lies entirely on the boundary of its convex
hull. It is proved that the optimization problem is
NP-complete. Nevertheless, linear greedy flooding
heuristics are used for generating convex decompo-
sitions. These heuristics work on the dual graph H of
mesh S, where nodes represents facets and arcs join
nodes associated with adjacent facets. The algorithm
starts from some node in H and traverses H, collect-
ing nodes along the way as long as the associated
facets form a convex sub-mesh. When no adjacent
nodes can be added to the current component, a new
component is started and the traversal resumes.
Another simple linear decomposition algorithm
is Watershed decomposition (Mangan and Whitaker,
1999) which decomposes a mesh into catchment
basins,orwatersheds. Let h : E → R be a discrete
height function defined over E, the set of elements
(vertices, edges or faces) of the mesh. A watershed
is a subset of E, consisting of elements whose path
of steepest descent terminates in the same local mini-
mum of h. In our implementation, the height function
is defined over the edges and is a function of the dihe-
dral angle.
The key idea of the Watershed decomposition algo-
rithm is to let the elements descend until a labeled re-
gion is encountered, where all the minima are labeled
as a first step.
The major problem with watershed as well as with
convex decomposition is over-segmentation (i.e., ob-
taining a large number of components), due to many
small concavities. The goal of our application, how-
ever, is to obtain only a handful of components.
To solve over-segmentation, it is proposed in (Man-
gan and Whitaker, 1999) to merge regions whose wa-
tershed depth is below a certain threshold. A cou-
ple of other possible solutions are studied in (Zucker-
berger et al., 2002) and described below.
First, since small components are less vital to
recognition (Biederman, 1987), the components are
merged based on their surface areas. Thus, a small
component is merged with a neighboring component
having the largest surface area. This process is done
in ascending order of surface areas and continues until
all the components become sufficiently large.
The drawback of merging is that it might result
with complex shapes, which might not fit any basic
shape.
Another solution is to ignore the small components
altogether. Only the original large components are
taken into account both in the construction of the
decomposition graph and in determining the compo-
nents’ basic shapes. The small components are used
only to determine the adjacency relations between the
large components.
Figure 2 presents an example of the results, ob-
tained by four variants of the general scheme: Convex
vs. Watershed decomposition and merging vs. ignor-
ing small components. As can be seen, even when
the small components are ignored, there is still suffi-
cient information to visually recognize the rook. Fig-
ures 2(c) demonstrates the drawback of merging – the
GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS
144

red component does not resemble any basic shape.
Convex Convex Watershed Watershed
merging ignoring merging ignoring
Figure 2: Decompositions of a rook.
In summary, the first step in constructing a sig-
nature of an object is to decompose it into a hand-
ful of meaningful components. This can be done by
augmenting linear algorithms – the watershed decom-
position and a greedy convex decomposition – with
a post-processing step which either eliminates small
components or merges them with their neighbors.
4 BASIC SHAPE
DETERMINATION
The second issue in the construction of a signature is
basic shape determination. Given a sub-mesh, which
basic shape better fits this component? In this paper
four basic shapes are considered – a spherical surface,
a cylindrical surface, a cone surface and a planar sur-
face.
Our problem is related to the problem of fit-
ting implicit polynomials to data and using polyno-
mial invariants to recognize three-dimensional ob-
jects. In (Taubin, 1991), a method based on mini-
mizing the mean square distance of the data points to
the surface is described. A first-order approximation
of the real distance is used. In (Keren et al., 1994),
a fourth-degree polynomial f(x,y,z) is sought, such
that the zero set of f(x,y,z) is stably bounded and
approximates the object’s boundary. A probabilistic
framework with an asymptotic Bayesian approxima-
tion is used in (Subrahmonia et al., 1996).
In order to fit a basic shape to a component, the
given component is first sampled. A non-linear least-
squares optimization problem, which fits each basic
shape to the set of sample points, is then solved. The
approximate mean square distance from the sample
points to each of the basic surfaces is minimized with
respect to a few parameters specific for each basic
shape. The basic shape with the minimal fitting error
represents the shape attribute of the component. The
algorithm for fitting the points to a surface is based on
(Taubin, 1991). We formalize it below.
Let f : R
n
→ R
k
be a smooth map, having continu-
ous first and second derivatives at every point. The set
of zeros of f, Z( f)={Y| f(Y)=0}, Y ∈ R
n
is defined
by the implicit equations f
1
(Y)=0,··· , f
k
(Y)=0
where f
i
(Y) is the i-th element of f,1≤ i ≤ k.
The goal is to find the approximate distance from
a point X ∈ R
n
to the set of zeros Z( f) of f.In
the linear case, the Jacobian matrix Jf(X) of f with
respect to X is a constant Jf(X)=C, and f (Y)=
f(X)+C(Y − X). The unique point
ˆ
Y that minimizes
the distance Y − X, constrained by f(Y)=0, is
given by
ˆ
Y = X − C
†
f(X), where C
†
= C
T
(CC
T
)
−1
is the pseudo-inverse (Duda et al., 2000). If C is in-
vertible then C
†
= C
−1
. Finally, the square of the dis-
tance from X to Z( f) is given by
dist (X, Z( f))
2
=
ˆ
Y − X
2
= f(X)
T
(CC
T
)
−1
f(X).
For the nonlinear case, Taubin (Taubin, 1991) pro-
poses to approximate the distance from X to Z( f)
with the distance from X to the set of zeros of a lin-
ear model of f at X,
˜
f : R
n
→ R
k
, where
˜
f is de-
fined by the truncated Taylor series expansion of f,
˜
f(Y)= f(X)+Jf(X)(Y − X). But,
˜
f(X)= f(X),
J
˜
f(X)=Jf(X), and the square of the approximated
distance from a point X ∈ R
n
to the set of zeros Z( f)
of f is given by
dist (X, Z( f))
2
≈ f(X)
T
(Jf(X)Jf(X)
T
)
−1
f(X).
Specifically, for the basic shapes we are considering,
n = 3, k = 1, and the set of zeros Z( f) of f is a surface
in three-dimensions. The Jacobian Jf(X) has only
one row and Jf(X)=(∇ f(X))
T
, where ∇ f(X) is the
gradient of f(X).
In this case, the approximated distance becomes
dist (X, Z( f))
2
≈ f(X)
2
/∇ f(X)
2
.
Moreover, we are interested in maps described
by a finite number of parameters (
α
1
,··· ,
α
r
). Let
φ
: R
n+r
→ R
k
be a smooth function, and consider
maps f : R
n
→ R
k
, which can be written as f(X) ≡
φ
(
α
,X), where
α
=(
α
1
,··· ,
α
r
)
T
, X =(X
1
,,··· ,X
n
)
and
α
1
,··· ,
α
r
are the parameters.
The approximated distance from X to Z(
φ
(
α
,X))
is then
dist (X, Z(
φ
(
α
,X)))
2
=
δ
φ
(
α
,X)
2
≈
φ
(
α
,X)
T
(J
φ
(
α
,X)J
φ
(
α
,X)
T
)
−1
φ
(
α
,X).
In particular, in three-dimensional space
δ
φ
(
α
,X)
2
≈
φ
(
α
,X)
2
/∇
φ
(
α
,X)
2
.
We can now formalize the fitting problem. Let P =
{p
1
,··· , p
m
} be a set of n-dimensional data points
and Z(
φ
(
α
,X)) the set of zeros of the smooth func-
tion
φ
(
α
,X). In order to fit P to Z(
φ
(
α
,X)) we need
to minimize the approximated mean square distance
∆
2
P
(
α
) from P to Z(
φ
(
α
,X)):
∆
2
P
(
α
)=
1
m
m
∑
i=1
δ
φ
(
α
, p
i
)
2
MESH RETRIEVAL BY COMPONENTS
145

with respect to the unknown parameters
α
=
(
α
1
,··· ,
α
r
)
T
.
This is equivalent to minimizing the length of the
residual vector Q =(Q
1
,··· ,Q
m
)
T
Q(
α
)
2
=
m
∑
i=1
Q
i
(
α
)
2
= m∆
2
P
(
α
)
where Q
i
(
α
)=
δ
φ
(
α
, p
i
), i = 1, ··· , m.
The Levenberg-Marquardt algorithm can be used to
solve this nonlinear least squares problem (Bates and
Watts, 1988). This algorithm iterates the following
step
α
n+1
=
α
n
−(JQ(
α
n
)JQ(
α
n
)
T
+
µ
n
I
m
)
−1
JQ(
α
n
)
T
Q(
α
n
),
where JQ(
α
) is the Jacobian of Q with respect to
α
:
J
ij
Q(
α
)=
∂
Q
i
∂α
j
(
α
), for i = 1,··· ,m, and j = 1,··· ,r,
and
µ
n
is a small nonnegative constant which makes
the matrix JQ(
α
n
)JQ(
α
n
)
T
+
µ
n
I
m
positive defined.
At each iteration, the algorithm reduces the length
of the residual vector, converging to a local minimum.
4.1 Distance 3D Point – Basic Shape
We can now explicitly define the square of the dis-
tance
δ
φ
(
α
,X) from a three-dimensional point X to
the set of zeros Z(
φ
(
α
,X)) of
φ
(
α
,X) for our ba-
sic shapes, three of which are quadrics (i.e., sphere,
cylinder, cone) and the fourth is linear (i.e., plane).
A quadric, in homogeneous coordinates, is given
by X
T
MX = 0 in the global coordinate system, where
M is a 4 × 4 matrix and X is a vector in R
4
. In its
local coordinate system, it is given by X
T
M
X
= 0,
where X = T
r
R
x
R
y
R
z
S
c
X
, T
r
is a translation matrix,
R
x
,R
y
,R
z
are rotation matrices and S
c
is a scale ma-
trix.
If M
is known, M can be calculated and the equa-
tion of the quadric in the global coordinate system can
be obtained.
φ
(t
x
,t
y
,t
z
,
θ
x
,
θ
y
,
θ
z
,s
x
,s
y
,s
z
,X)=X
T
MX = 0,
where the parameters are the translation, rotation and
scale.
Then, for each basic quadric, the square of the ap-
proximated distance
δ
φ
(t
x
,t
y
,t
z
,
θ
x
,
θ
y
,
θ
z
,s
x
,s
y
,s
z
,X
p
)
from a three-dimensional point X
p
to the quadric can
be determined by
δ
φ
(t
x
,t
y
,t
z
,
θ
x
,
θ
y
,
θ
z
,s
x
,s
y
,s
z
,X
p
)
2
≈ (1)
≈
φ
(t
x
,t
y
,t
z
,
θ
x
,
θ
y
,
θ
z
,s
x
,s
y
,s
z
,X
p
)
2
∇
φ
(t
x
,t
y
,t
z
,
θ
x
,
θ
y
,
θ
z
,s
x
,s
y
,s
z
,X
p
)
2
=
=
φ
(t
x
,t
y
,t
z
,
θ
x
,
θ
y
,
θ
z
,s
x
,s
y
,s
z
,X
p
)
2
(
∂φ
∂
x
)
2
+(
∂φ
∂
y
)
2
+(
∂φ
∂
z
)
2
Hereafter we use the above equation to calculate
δ
φ
for each quadric basic shape, which are all special
cases of the above.
For a spherical surface with radius r
0
= 1, defined
in its local coordinate system centered at the center of
the sphere, we have
M
=
⎛
⎜
⎝
100 0
010 0
001 0
000−1
⎞
⎟
⎠
.
φ
(t
x
,t
y
,t
z
,r, x,y, z)=(x−t
x
)
2
+(y−t
y
)
2
+(z−t
z
)
2
−r
2
= 0.
For a cylindrical surface with radius r
0
= 1, defined
in its local coordinate system, where the z axis is the
axis of the cylinder,
M
=
⎛
⎜
⎝
100 0
010 0
000 0
000−1
⎞
⎟
⎠
.
The implicit equation in the global coordinate sys-
tem is
φ
(t
x
,t
y
,t
z
,
θ
x
,
θ
y
,r,x, y,z)= (2)
= D
1
(x−t
x
)
2
+ D
2
(y−t
y
)
2
+ D
3
(z−t
z
)
2
+
+2C
1
(x−t
x
)(y−t
y
)+2C
2
(x−t
x
)(z−t
z
)+
+2C
3
(y−t
y
)(z−t
z
) − r
2
= 0
where
D
1
= cos
2
θ
y
,
D
2
= cos
2
θ
x
+ sin
2
θ
x
sin
2
θ
y
,
D
3
= sin
2
θ
x
+ cos
2
θ
x
sin
2
θ
y
,
C
1
= sin
θ
x
sin
θ
y
cos
θ
y
,
C
2
= − cos
θ
x
sin
θ
y
cos
θ
y
,
C
3
= sin
θ
x
cos
θ
x
cos
2
θ
y
,
B
1
= −t
x
D
1
−t
y
C
1
−t
z
C
2
,
B
2
= −t
x
C
1
−t
y
D
2
−t
z
C
3
,
B
3
= −t
x
C
2
−t
y
C
3
−t
z
D
3
.
Note that (t
x
,t
y
,t
z
) can be any point on the cylinder
axis, thus the cylinder is over parameterized. This can
be solved by setting one of these three parameters to
zero.
For a cone surface with g
0
= r
0
/h
0
= 1, where r
0
is the radius and h
0
is the height, defined in its local
coordinate system, where the z axis is the axis of the
cone and the origin of the coordinate system is the
apex of the cone,
M
=
⎛
⎜
⎝
10 0 0
01 0 0
00−10
00 0 0
⎞
⎟
⎠
.
The implicit equation in the global coordinate sys-
tem is
φ
(t
x
,t
y
,t
z
,
θ
x
,
θ
y
,g,x, y,z)= (3)
= D
1
(x−t
x
)
2
+ D
2
(y−t
y
)
2
+ D
3
(z−t
z
)
2
+
+2C
1
(x−t
x
)(y−t
y
)+2C
2
(x−t
x
)(z−t
z
)+
+2C
3
(y−t
y
)(z−t
z
)=0
GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS
146

where
D
1
= cos
2
θ
y
− g
2
sin
2
θ
y
,
D
2
= cos
2
θ
x
+ sin
2
θ
x
sin
2
θ
y
− g
2
sin
2
θ
x
cos
2
θ
y
,
D
3
= sin
2
θ
x
+ cos
2
θ
x
sin
2
θ
y
− g
2
cos
2
θ
x
cos
2
θ
y
,
C
1
=(1+ g
2
)sin
θ
x
sin
θ
y
cos
θ
y
,
C
2
= −(1+ g
2
)cos
θ
x
sin
θ
y
cos
θ
y
,
C
3
=(1+ g
2
)sin
θ
x
cos
θ
x
cos
2
θ
y
,
B
1
= −t
x
D
1
−t
y
C
1
−t
z
C
2
,
B
2
= −t
x
C
1
−t
y
D
2
−t
z
C
3
,
B
3
= −t
x
C
2
−t
y
C
3
−t
z
D
3
.
Finally, a plane is defined by the equation ax+by+
cz + d = 0. The square of the distance from a point
p =(x
p
,y
p
,z
p
) to the plane is simply
δ
φ
(a,b,c,d,x
p
,y
p
,z
p
)
2
=
(ax
p
+ by
p
+ cz
p
+ d)
2
a
2
+ b
2
+ c
2
.
5 EXPERIMENTAL RESULTS
Our goal is to examine whether Biederman’s observa-
tion, claiming that recognition can be accurate even if
only a few geons of a complex object are visible (Bie-
derman, 1995), is indeed feasible.
We tested our retrieval algorithm on a database con-
sisting of 388 objects. Among the 388 objects we
identified six classes: 19 models of human figures, 18
models of four-legged animals, 9 models of knives, 8
models of airplanes, 7 models of missiles and 7 mod-
els of bottles. The other models are unclassified.
Four different decomposition techniques were used
in our experiments: (1) Greedy convex decomposi-
tion, where small patches are ignored; (2) Greedy
convex decomposition, where small patches are
merged with their neighbors; (3) Watershed decom-
position, where small patches are ignored; (4) Water-
shed decomposition, where small patches are merged
with their neighbors.
Based on these four decomposition techniques,
four signature databases were built. Identical retrieval
experiments were applied to each database. In each
experiment, a test object was chosen and the system
was queried to retrieve the most similar objects to this
test object in ascending order. At least one member
from each of the six classes was used as a test object.
Figures 3– 6 demonstrate some of our results. In
each figure, the test object is the left-most, top ob-
ject, and the objects retrieved are ranked from left to
right. In particular, Figure 3 presents the most similar
objects to Detpl (at the top-left), as retrieved by our
algorithm. All the eight airplanes of the class were
retrieved among the top eleven. Figure 4 presents
the results of retrieving objects similar to Cat2. Six-
teen out the eighteen members of the 4-legged animal
class were retrieved among the top twenty. Figure 5
presents the retrieved most similar objects to Knifech.
Eight out of the nine knifes of the class were retrieved
among the top ten. Figure 6 demonstrates the most
similar objects to the missile at the top left, as re-
trieved by our algorithm. Six out of the the seven class
members were retrieved among the top nine. Note
that in all the above cases the members of each class
differ geometrically. Yet, their decomposition graphs
are similar and therefore they were found to be simi-
lar.
Figure 3: The most similar objects to Detpl (top left).
Figure 4: The most similar objects to Cat2.
Figure 5: The most similar objects to Knifech.
On the class of bottles, the algorithm does not per-
form as well. This class contains seven members (see
Figure 7). Though the objects seem similar geomet-
rically, their connectivity differs. The Beer, Ketchup
and Tabasco bottles consist each of 4-8 disconnected
components while Bottle3, Champagne, Whiskey and
Plastbtl consist each of only one or two components.
MESH RETRIEVAL BY COMPONENTS
147
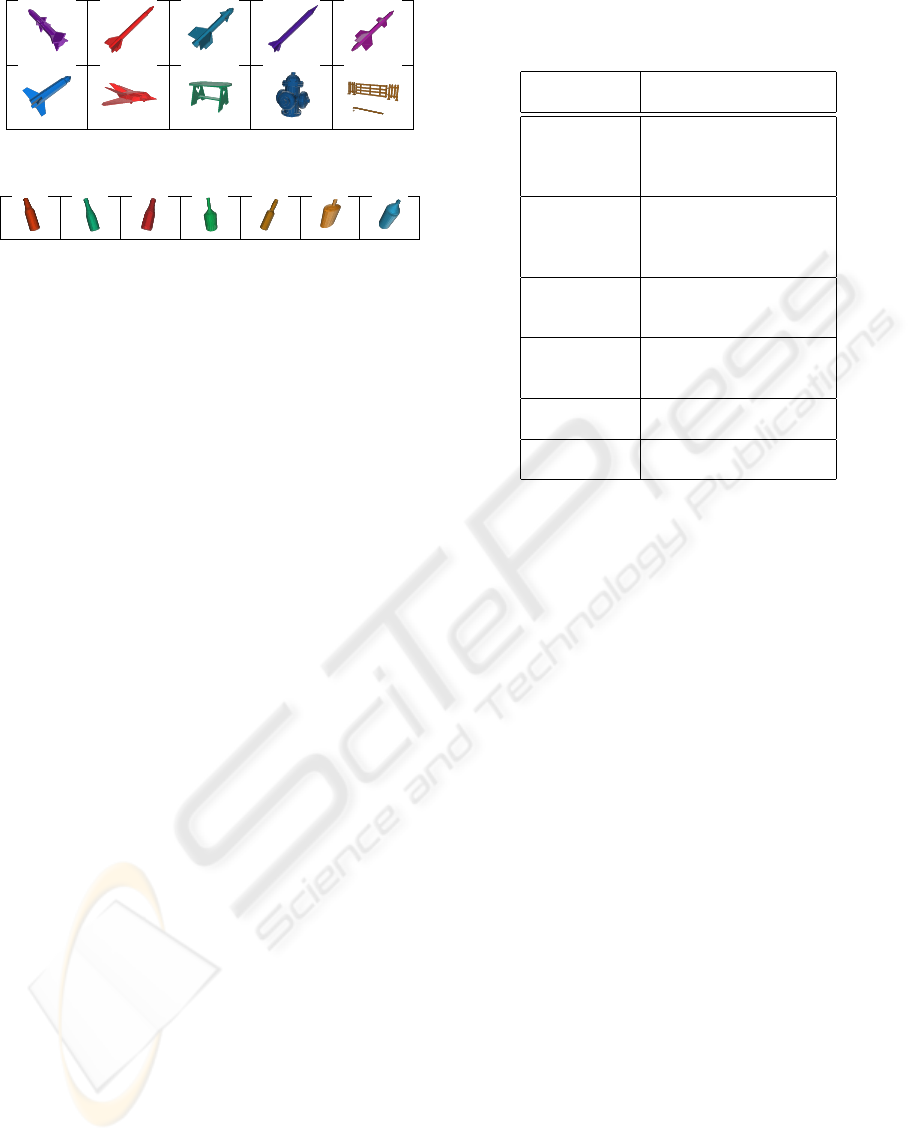
Figure 6: The most similar objects to Aram.
Figure 7: The bottle class.
Since connectivity determines the graph structure and
the graphs differ, the results of the retrieval experi-
ments are inferior to the other classes.
All four sub-methods performed well. The Wa-
tershed decomposition performed slightly better than
convex decomposition. This fact might be surprising
since convexity is the main factor in human segmen-
tation. This can be explained by the fact that optimal
convex decomposition cannot be achieved. Moreover,
the height function used in the Watershed algorithm
considers convexity as well.
Considering only the original large components
and ignoring the small ones performs better than
merging small components with their neighbors, both
for watershed decomposition and for convex decom-
position. This can be explained by the fact that merg-
ing results in complex shapes which might cause a
failure of the basic shape determination procedure.
Table 1 shows some of our results for one sub-
method – Watershed, ignoring small components.
The first column shows the classes and the test ob-
jects. For each class, the number of members of the
class N is shown. The next column of the table sum-
marizes the results obtained for each test object. Each
result (n/m) represents the number of the members of
the same class n retrieved among the top m objects.
6 CONCLUSION
This paper examines the adaptation of the human vi-
sion theories of Marr and Biederman to three dimen-
sions. According to these theories, an object is repre-
sented by an attributed graph, where each node repre-
sents a meaningful component of the object, and there
are arcs between nodes whose corresponding compo-
nents are adjacent in the model. Every node is at-
tributed with the basic shape found to best match the
component, while each arc is attributed with the rela-
tive surface area of its adjacent nodes.
It was demonstrated that simple and efficient de-
composition algorithms suffice to construct such a
Table 1: Summary of the experimental results for the Wa-
tershed / ignore sub-method.
Class(N)/
Object Retrieved / Top results
Airplanes(8)
Detplane 5/6 7/9 8/16
Worldw 6/6 6/9 8/16
747 5/6 5/9 7/16
Animals(18)
Cat2 6/8 11/14 14/20
Tiger3 7/8 11/14 13/20
Deer 8/8 11/14 15/20
Humans(19)
Woman2 10/10 17/17 19/24
Child3y 10/10 15/17 19/24
Knives(9)
Knifech 6/6 8/8 8/15
Knifest 6/6 6/8 8/15
Missiles(7)
Aram 3/6 5/10
Bottles(7)
Beer 1/3 1/6
signature. We examined a couple of post-processing
steps on top of well-known segmentation algorithms,
in order to get only a handful of components. More-
over, a technique was presented for finding the best
match between a given sub-mesh and pre-defined ba-
sic shapes. An error-correcting subgraph isomor-
phism algorithm was used for matching.
The experimental results presented in the paper are
generally good. The major benefits of the signature
is being invariant to non-rigid transformations and
avoiding normalization as a pre-processing step. In
addition, the algorithm for generating signatures is
simple and efficient and produces very compact sig-
natures.
The technique has a couple of drawbacks. First,
the signature depends on the connectivity of the given
objects, which might cause geometrically-similar ob-
jects to be considered different. Second, the graph
matching algorithm we use is relatively slow. While
the first drawback can be solved by fixing the models,
the second problem is inherent to graph-based repre-
sentations. More efficient graph matching algorithms
should be sought.
REFERENCES
Bates, D. and Watts, D. (1988). Nonlinear Regression and
Its Applications. John Wiley & Sons, New York.
Biederman, I. (1987). Recognition-by-components: A the-
ory of human image understanding. Psychological Re-
view, 94:115–147.
GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS
148

Biederman, I. (1988). Aspects and extensions of a theory
of human image understanding. Pylyshyn Z. editor,
Computational Processes in Human Vision: An Inter-
disciplinary Perspective, pages 370–428.
Biederman, I. (1995). Visual object recognition. S. Koss-
lyn, D. Osherson, editors. An Invitation to Cognitive
Science, 2:121–165.
Chazelle, B., Dobkin, D., Shourhura, N., and Tal, A. (1997).
Strategies for polyhedral surface decomposition: An
experimental study. Computational Geometry: The-
ory and Applications, 7(4-5):327–342.
Cornea, N., Demirci, M., Silver, D., Shokoufandeh, A.,
Dickinson, S., and Kantor, P. (2005). 3D object re-
trieval using many-to-many matching of curve skele-
tons. In IEEE International Conference on Shape
Modeling and Applications, pages 368–373.
Duda, R., Hart, P., and Stork, D. (2000). Pattern Classifica-
tion. John Wiley & Sons, New York.
Elad, M., Tal, A., and Ar, S. (2001). Content based retrieval
of vrml objects - an iterative and interactive approach.
EG Multimedia, 39:97–108.
Hilaga, M., Shinagawa, Y., Kohmura, T., and Kunii, T.
(2001). Topology matching for fully automatic sim-
ilarity estimation of 3D shapes. SIGGRAPH, pages
203–212.
Katz, S., Leifman, G., and Tal, A. (2005). Mesh segmen-
tation using feature point and core extraction. The Vi-
sual Computer, 21(8-10):865–875.
Katz, S. and Tal, A. (2003). Hierarchical mesh decompo-
sition using fuzzy clustering and cuts. ACM Trans.
Graph. (SIGGRAPH), 22(3):954–961.
Kazhdan, M., Chazelle, B., Dobkin, D., and Funkhouser,
T. (2003a). A reflective symmetry descriptor for 3D
models. Algorithmica, page to appear.
Kazhdan, M., Funkhouser, T., and Rusinkiewicz, S.
(2003b). Rotation invariant spherical harmonic rep-
resentation of 3D shape descriptors. In Symposium on
Geometry Processing.
Keren, D., Cooper, D., and Subrahmonia., J. (1994). De-
scribing complicated objects by implicit polynomials.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, 16(1):38–53.
Lee, S., Kim, J., and Groen, F. (1990). Translation-
, rotation-, and scale-invariant recognition of hand-
drawn symbols in schematic diagrams. Int. J. Pattern
Recognition and Artificial Intelligence, 4(1):1–15.
Lee, Y., Lee, S., Shamir, A., Cohen-Or, D., and Seidel, H.-
P. (2005). Mesh scissoring with minima rule and part
salience. Computer Aided Geometric Design.
Leifman, G., Meir, R., and Tal, A. (2005). Semantic-
oriented 3D shape retrieval using relevance feedback.
The Visual Computer, 21(8-10):649–658.
Li, X., Toon, T., Tan, T., and Huang, Z. (2001). Decompos-
ing polygon meshes for interactive applications. In
Proceedings of the 2001 symposium on Interactive 3D
graphics, pages 35–42.
Mangan, A. and Whitaker, R. (1999). Partitioning 3D sur-
face meshes using watershed segmentation. IEEE
Transactions on Visualization and Computer Graph-
ics, 5(4):308–321.
Marr, D. (1982). Vision - A computational investigation into
the human representation and processing of visual in-
formation. W.H. Freeman, San Francisco.
Messmer, B. (1995). GMT - Graph Matching Toolkit. PhD
thesis, University of Bern.
Osada, R., Funkhouser, T., Chazelle, B., and Dobkin, D.
(2001). Matching 3D models with shape distribu-
tions. In Proceedings of the International Conference
on Shape Modeling and Applications, pages 154–166.
Paquet, E., Murching, A., Naveen, T., Tabatabai, A., and
Rioux, M. (2000). Description of shape information
for 2-D and 3-D objects. Signal Processing: Image
Communication, pages 103–122.
Pearce, A., Caelli, T., and Bischof, W. (1994). Rulegraphs
for graph matching in pattern recognition. Pattern
Recognition, 27(9):1231–1246.
Rocha, J. and Pavlidis, T. (1994). A shape analysis model
with applications to a character recognition system.
IEEE Trans. Pattern Analysis and Machine Intelli-
gence, 16:393–404.
Shamir, A. (2004). A formalization of boundary mesh seg-
mentation. In Proceedings of the second International
Symposium on 3DPVT.
Subrahmonia, J., Cooper, D., and Keren, D. (1996). Practi-
cal reliable bayesian recognition of 2d and 3D objects
using implicit polynomials and algebraic invariants.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, 18(5):7505–519.
Sundar, H., Silver, D., Gagvani, N., and Dickinson, S.
(2003). Skeleton based shape matching and retrieval.
In Shape Modelling and Applications.
Taubin, G. (1991). Estimation of planar curves, surfaces,
and nonplanar space curves defined by implicit equa-
tions with applications to edge and range image seg-
mentation. IEEE Transactions on Pattern Analysis
and Machine Intelligence, 13(11):1115–1138.
Veltkamp, R. (2001). Shape matching: Similarity measures
and algorithms. In Shape Modelling International,
pages 188–197.
Vranic, D. and Saupe, D. (2002). Description of 3D-shape
using a complex function on the sphere. In Proceed-
ings IEEE International Conference on Multimedia
and Expo, pages 177–180.
Wang, Y.-K., Fan, K.-C., and Horng, J.-T. (1997). Genetic-
based search for error-correcting graph isomorphism.
IEEE Trans. Systems, Man, and Cybernetics, 27:588–
597.
Wong, E. (1992). Model matching in robot vision by sub-
graph isomorphism. Pattern Recognition, 25(3):287–
304.
Zuckerberger, E., Tal, A., and Shlafman, S. (2002). Poly-
hedral surface decomposition with applications. Com-
puters & Graphics, 26(5):733–743.
MESH RETRIEVAL BY COMPONENTS
149
