
A NEW NON-UNIFORM LOOP SCHEME
Sandrine Lanquetin, Marc Neveu
LE2I, UMR CNRS 5158, UFR des Sciences et Techniques,
Université de Bourgogne, BP 47870
21078 DIJON Cedex, France
Keywords: Adaptive subdivision, non uniform scheme, Loop scheme.
Abstract: In this paper, we introduce a new non-uniform Loop scheme. It refines selected areas which are chosen
manually or automatically according to the precision of the control mesh compared to the limit surface. Our
algorithm avoids cracks and generates a progressive mesh with a difference of at most one subdivision level
between two adjacent faces. As adaptive subdivision is repeated, subdivision depth changes gradually from
one area of the surface to another area. Moreover generated meshes remain a regular valence. Results
obtained from our scheme are compared to those of the T-algorithm and the incremental algorithm.
1 INTRODUCTION
Subdivision surfaces were introduced in 1978 by
Catmull-Clark (Catmull et al., 1978) and Doo-Sabin
(Doo et al., 1978) as an extension of the Chaikin
algorithm (Chaikin, 1974)]. These surfaces are
widely used in character animation (such as Geri's
Game © or Finding Nemo ©) to smooth models.
Indeed, from a coarse mesh, successive refinements
give finer meshes. A sequence of subdivided meshes
converges towards a smooth surface called limit
surface. Since the beginning of subdivision surfaces
in 1978, many subdivision schemes were proposed.
Some are approximating and others are interpolating
(i.e. control vertices of successive meshes belong to
the limit surface). We focus on Loop subdivision
(Loop, 1987) for this research. This scheme is
approximating and can only be applied on triangular
meshes.
Most of schemes were first uniform. In uniform
schemes, the subdivision rules are the same for the
whole input model. For example, the Loop scheme
splits each face of the input mesh into four. The
number of faces quickly increases whereas there is
generally no need to smooth the model everywhere.
Indeed, subdivisions do not bring much geometric
modification into flat areas; faces which are not
visible do not need many subdivisions. Other
geometric criteria can be used such as accuracy or
curvature. Or more simply, users can manually
choose faces or vertices to be subdivided.
Non uniform subdivision (also called adaptive
subdivision) can be decomposed into two parts.
First, an area to be subdivided has to be chosen by
different ways such as in (Amresh et al., 2003),
(Dyn et al., 1990), (Meyer et al., 2002), (Zorin et al.,
1998). Secondly, topological rules have to be
determined such as in (Amresh et al., 2003), (Pakdel
et al., 2004), (Seeger et al., 2001), (Zorin et al.,
1998). These rules aim to generate a new mesh
without the cracks that can be caused by a difference
between the subdivision levels of two adjacent faces.
In the case of Loop’s triangular scheme, rules have
to preserve triangular faces.
In this paper, we focus on the topological problem.
Some algorithms already deal with this subject.
Thus, the algorithm of Seeger et al. splits adjacent
faces into two if they present a crack and into four
otherwise (Seeger et al., 2001). Amresh et al.
similarly propose to split faces into two, three or
four faces according to the number of cracks created
by the face subdivision (Amresh et al., 2003). From
these algorithms, Pakdel and Samavati extend the
rules to produce a smooth surface with visually
pleasing connectivity (Pakdel et al., 2004).
Our contribution consists in new topological rules
for non-uniform Loop subdivision. The algorithm
we propose takes advantages of the above mentioned
algorithms. Indeed, our algorithm produces meshes
with progressive changes between faces of different
subdivision level but without subdividing a too large
134
Lanquetin S. and Neveu M. (2006).
A NEW NON-UNIFORM LOOP SCHEME.
In Proceedings of the First International Conference on Computer Graphics Theory and Applications, pages 134-141
DOI: 10.5220/0001350301340141
Copyright
c
SciTePress
surrounding area. Obviously, the more extended the
area is, the higher the number of generated faces is.
The paper is organized as follows. Section 2 is an
overview of uniform and non-uniform Loop
schemes. In section 3, we explain disadvantages and
advantages of existing adaptive schemes and how
our algorithm works. Finally, we compare our
algorithm with the others on some examples in
section 4.
2 BACKGROUND
2.1 Loop Scheme
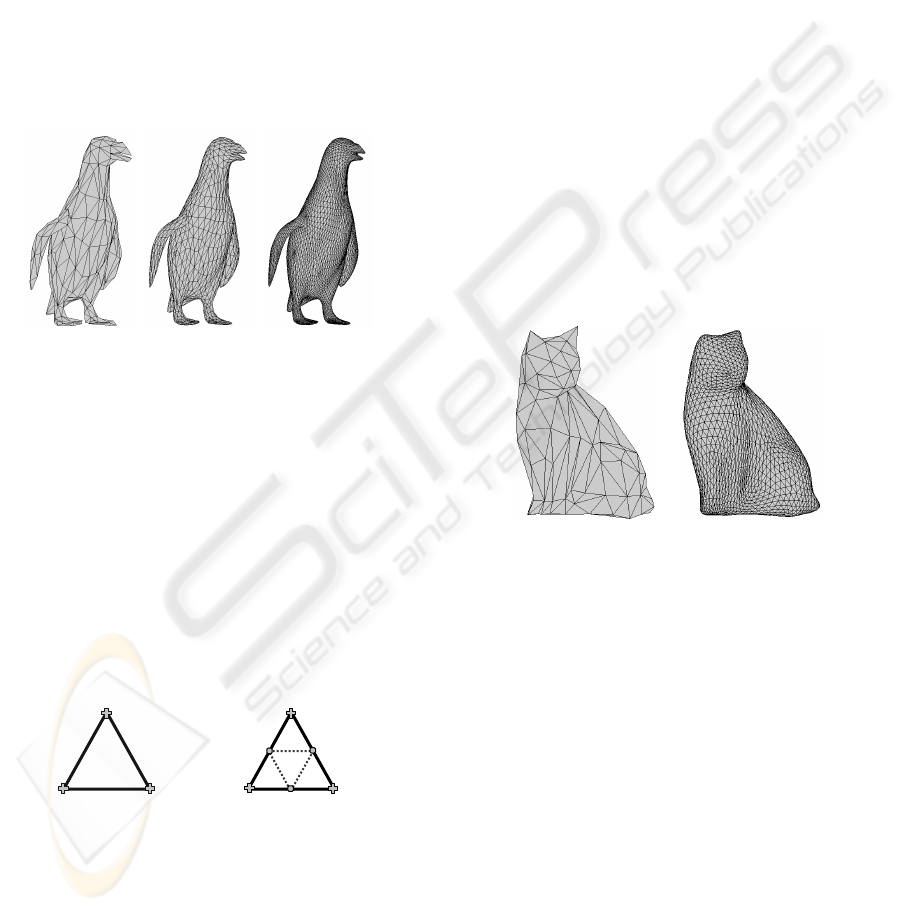
Figure 1: From left to right: the initial penguin mesh and
two successive levels of Loop subdivision.
Subdivision surfaces are defined by an initial control
mesh and a set of refinement rules. The application
of refinement rules generates a sequence of
increasingly fine control meshes. Control meshes are
often referred to as polygonal meshes or
polyhedrons. The sequence of control meshes
converges to a smooth surface called the limit
surface. There are two sorts of subdivision schemes:
schemes which rely on interpolation (e.g. Butterfly
scheme (Dyn et al., 1990)) or approximation (e.g.
Catmull-Clark (Catmull et al., 1978), Doo-Sabin
(Doo et al., 1978), Loop (Loop, 1987) schemes…).
Figure 2: Left, an initial face. Right, the 4 new faces.
A particularity of approximation schemes is that
control meshes approach the limit surface at each
step of refinement. Figure 1 shows three successive
meshes obtained by applying Loop scheme.
The Loop scheme generalizes quadratic triangular
B-splines and the obtained limit surface is a quartic
Box-spline. This scheme is based on face splitting:
each face of the control mesh at refinement level
k
is subdivided into four new triangular faces at level
1k
+
. This first step is illustrated in Figure 2.
Consider a face: new vertices -named odd vertices-
are inserted in the middle of each edge, and those of
the initial face are named even vertices. In the
second step, all vertices are displaced by computing
a weighted average of the vertex and its
neighbouring vertices. These averages can be
substituted by applying different masks according to
vertex properties: even/odd, interior/boundary
2.2 Adaptive Subdivision
When the same rules are applied on the whole input
mesh, the number of faces quickly increases. Indeed,
for Loop scheme, a face produces four faces after
one subdivision,
2
4 after 2 subdivisions and 4
n
after
n subdivisions. Thus, the cat model introduced in
Figure 3 has 224 faces at the initial level (Figure 3,
left) and 3584 after two subdivisions (Figure 3,
right).
Figure 3: Left: the initial cat model. Right: the cat mesh
after two subdivisions.
However, there is often no need to smooth the
model in the same way everywhere according to
surface properties or specific applications. For
example, if a surface is flat, there is no need to
subdivide it anymore. Indeed, in this case, new
generated faces do not improve quality of the mesh.
In a similar way, an area of the mesh which already
looks smooth will not change anymore after new
subdivision levels. Another idea is to smooth only
visible parts of the mesh. The mesh can also be
subdivided only where the mesh does not
approximate the limit surface with enough precision.
Thus, only some areas of the input mesh can be
subdivided to generate an optimal mesh with a
smaller number of faces.
When the surface is not entirely subdivided,
cracks appear between faces with different
subdivision levels as shown in Figure 4.
A NEW NON-UNIFORM LOOP SCHEME
135
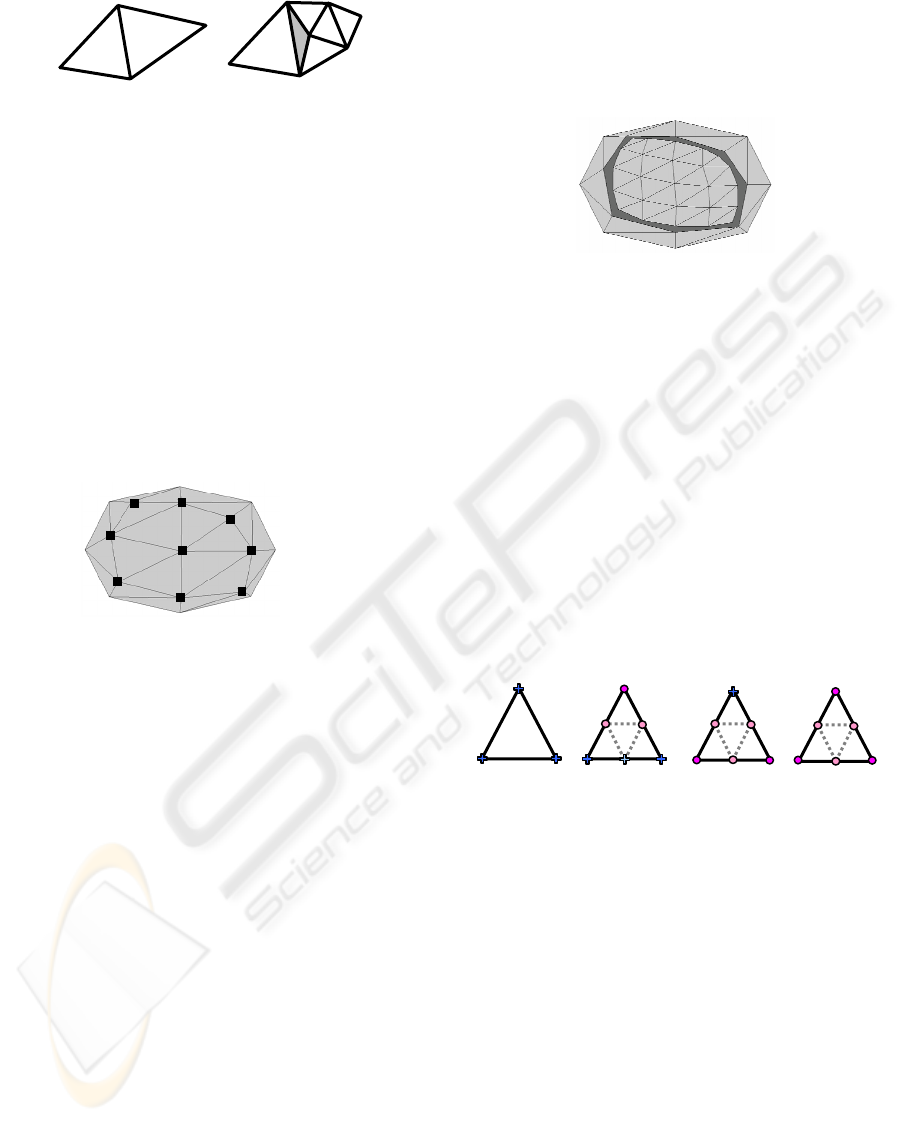
Figure 4: Left: two adjacent faces of the mesh. Right: one
face is subdivided and not the other, the crack between the
faces is represented in grey.
To avoid cracks, topological rules have to be
modified. As rules are different according to
subdivision areas, this kind of scheme is called non-
uniform or adaptive.
Selection criteria. The area to be subdivided can be
selected by different ways.
First, users can manually choose faces or vertices
they want to subdivide. This choice can be done
arbitrarily or according to the required details in a
specific area. Figure 5 illustrates a mesh with
selected vertices to be subdivided in dark grey.
Figure 5: Example of manual selection.
Another criterion for adaptive subdivision, which
is often used, is the surface curvature. In this case,
the model is refined where the model has high
curvatures. Thus, Dyn et al. (Dyn et al., 2000)
automatically determine the area to subdivide
according to the discrete curvature and apply it on
the butterfly scheme. Meyer et al. compute Gaussian
curvature from its sums of Voronoi area (Meyer et
al., 2002). Others works are based on
approximations of the surface curvatures which are
easier to compute. Xu and Kondo (Xu et al., 1999)
and Amresh et al. (Amresh et al., 2003) use the
dihedral angle criterion (the angle between normals
of adjacent faces). Müller and Havemann (Müller et
al., 2000) propose another approximation of the
surface curvature by computing, for each vertex of
the mesh, the normal cone (the angle between
normals of adjacent faces to a vertex). Another
criterion can be the accuracy of the control mesh
compared to the limit surface (Lanquetin, 2004). In
(Isenberg et al., 2003), Isenberg et al. generalizes
adaptive subdivision algorithms by introducing an
application-dependent Degree of Interest function.
Topological rules. To avoid cracks which appear
when the surface is not entirely subdivided, there
exist different methods. Figure 6 shows these cracks
on a mesh for which only faces selected in Figure 5
are subdivided with Loop scheme.
Figure 6: Example of cracks.
Various topological rules were already proposed in
(Amresh et al., 2003), (Lanquetin, 2004), (Pakdel et
al., 2004), (Seeger et al., 2001) and (Zorin et al.,
1998). We will describe them in section 3.
3 TOPOLOGICAL RULES
3.1 Existing Topological Rules
A simple method presented in (Lanquetin, 2004) and
used in (Lanquetin et al., 2004) generates a
minimum number of faces. The surface is only
subdivided where the distance is greater than a given
threshold.
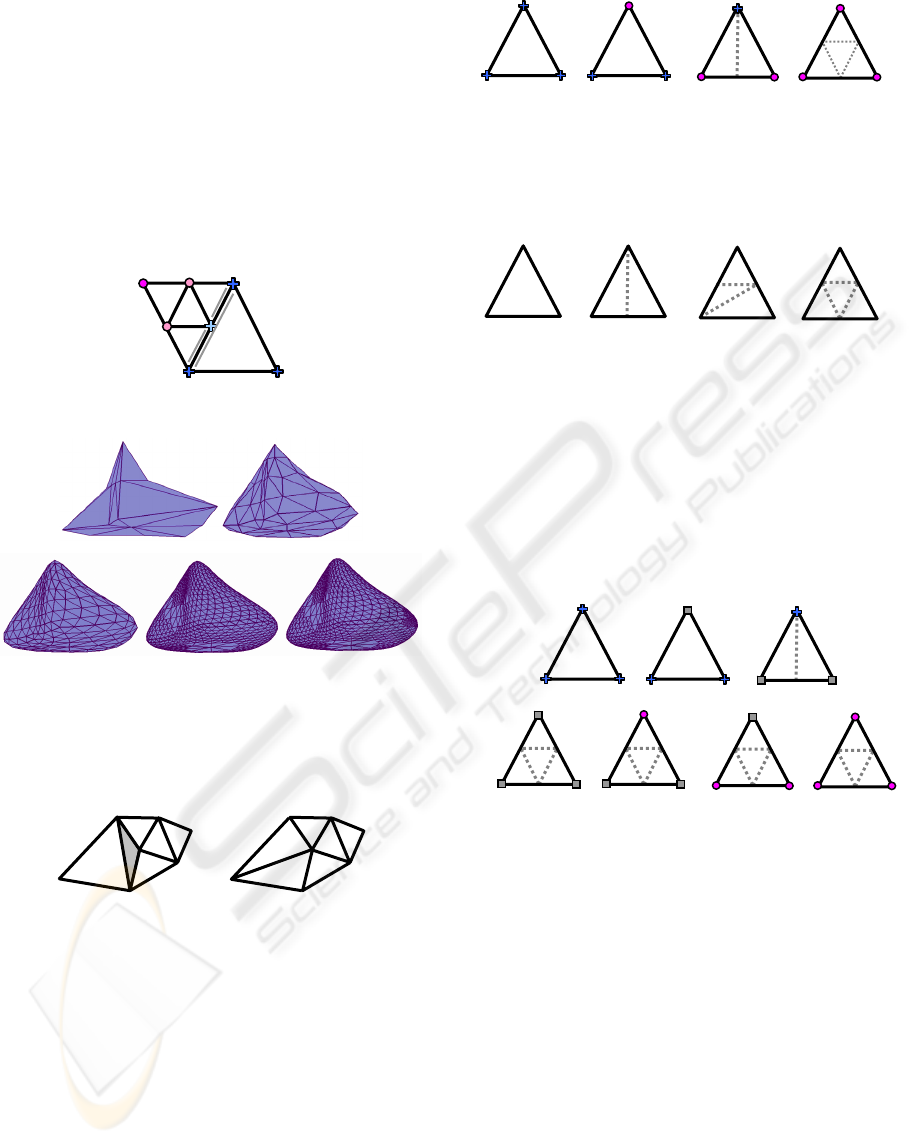
Figure 7: Different cases of subdivision in the simple
adaptive subdivision.
Let us first define the terms used to explain how
faces are subdivided in this adaptive subdivision: a
vertex which is not displaced is called static and a
vertex which is displaced is called mobile. Faces are
classified into 4 categories according to the number
of mobile vertices. Mobile vertices are depicted by
circles in Figure 7. When all vertices are static, the
face is not subdivided (Figure 7.a.). Figure 7.b.
illustrates the case where only one vertex is mobile;
only two among the three new vertices are then
mobile in order to avoid cracks. When there are two
mobile vertices, face subdivision is almost normal
except for the fact that one of the old vertices is
static (Figure 7.c.). Finally when all vertices are
mobile, subdivision is carried out in a normal way
(Figure 7.d.).
a.
c. d. b.
GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS
136
This scheme generates a minimum number of
faces because faces which have 3 static points are no
more subdivided. This adaptive subdivision scheme
avoids cracks but the resulting mesh is not
conformal (Figure 9). Indeed, the case shown in
Figure 8 appears between subdivided faces and not.
The edge of the face which is not subdivided
corresponds to two edges of subdivided faces. In
Figure 8, vertices represented by crosses are no more
subdivided and those represented by circles are still
subdivided.
Figure 8: New neighbourhood.
Figure 9: Successive mesh subdivisions with without
proper neighbourhood.
Following methods reconstruct a proper mesh
after successive subdivisions.
Figure 10: Left: one face is subdivided and not the other,
the crack between faces is represents in grey. Right:
bisection of adjacent faces by an edge to avoid cracks.
Zorin et al. (Zorin et al., 1998) and Amresh et al.
(Amresh et al., 2003) remove cracks in subdividing
chosen faces and bisecting adjacent faces by an
edge. The bisection is done in connecting the vertex
with the incomplete structure to the opposite vertex
of the adjacent face as shown in Figure 10.
In Figure 11, mobile vertices are denoted by
circles and others by crosses. In the following, this
scheme will be called T-algorithm.
Figure 11: Topological rules for the T-algorithm.
Seeger et al. (Seeger et al., 2001) focus on the
butterfly scheme. Their algorithm, called red-green
triangulation, splits faces into two, three or four
faces as illustrated in Figure 12.
Figure 12: Different cases of face splitting used in the red-
green algorithm.
Pakdel and Samavati (Pakdel et al., 2004) extend
the method introduced in (Amresh et al., 2003) to
remove cracks after adaptative subdivision. To
maintain a restricted mesh (Zorin et al., 1998) during
subdivision, they select a larger subdivision area
than the specified one. They call their algorithm
incremental algorithm. They introduce progressive
vertices, denoted by squares in Figure 13.
Figure 13: Topological rules for the incremental
algorithm.
Each vertex in the 1-neighbourhood of the
selected area is tagged as progressive. Then,
according to the vertex tag: mobile (circle),
progressive (square) or static (cross), faces are
subdivided as illustrated in Figure 13.
A NEW NON-UNIFORM LOOP SCHEME
137
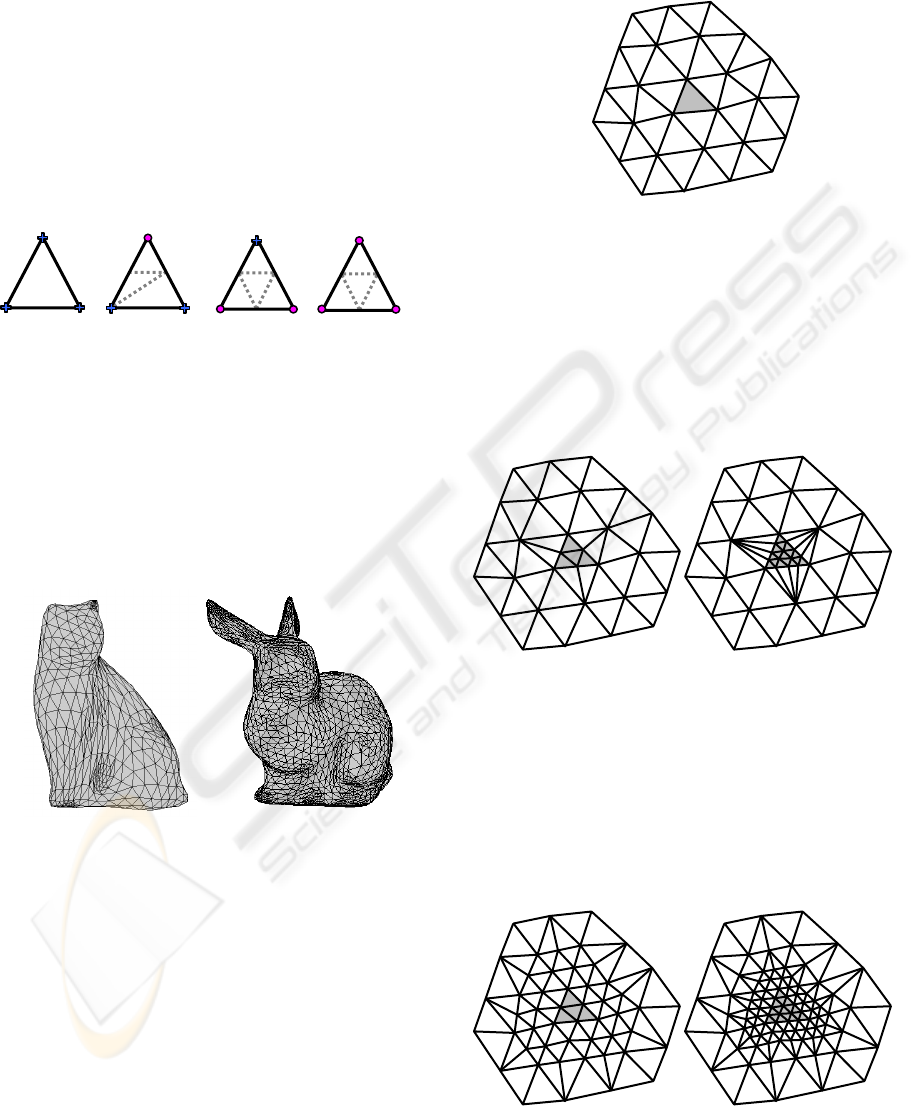
3.2 Our Topological Rules
Our algorithm takes advantages of both T-algorithm
and incremental algorithm. In the following this
scheme will be called diagonal algorithm. It selects a
larger subdivision area than the T-algorithm but a
smaller one than the incremental algorithm. Faces
selected are normally subdivided. Then, adjacent
faces by an edge are split into four and adjacent
faces by a vertex are split into three as shown in
Figure 14. Vertices to be subdivided are denoted by
circles and others by crosses.
Figure 14: Topological rules for the diagonal algorithm.
In contrast with the T-algorithm, the diagonal
algorithm removes cracks outside the selected area
so that the subdivision is progressive and new
valences are not too high. Indeed, adjacent faces are
at most one subdivision depth apart, so the
connectivity between faces does not abruptly
change. As vertices where trisection is applied once
are no more subdivided, the valence of this vertex no
more increases. This avoids generating too high
valences.
Figure 15: Subdivision of the cat and the bunny models
with the diagonal adaptive algorithm.
Moreover, contrary to incremental algorithm, the
additional selected area is smaller so that the final
mesh has less faces. Indeed the goal of adaptive
subdivision is to generate meshes with less faces.
Meshes obtained on the cat and the bunny models
are shown in Figure 15.
3.3 Successive Subdivisions
Differences between the T-algorithm, the
incremental algorithm and the diagonal algorithm
are now shown on an example. Let the initial mesh
be the mesh drawn in Figure 16 and the selected area
be the face in grey.
Figure 16: The selected face to subdivide is in grey.
The three algorithms will now be applied on the
mesh in Figure 16. Figure 17 shows two subdivision
levels obtained with the T-algorithm. The number
of faces is 43 after one subdivision and 61 after two.
So there are few generated faces. However, at the
second subdivision level, some introduced valences
are extraordinary and become higher and higher with
successive subdivisions.
Figure 17: Two subdivisions of the grey face with the T-
algorithm.
To avoid this problem of high valences, the
incremental algorithm takes a larger area around the
selected faces. Results of one and two subdivisions
are illustrated in Figure 18.
The number of faces is very high from the first
subdivision: 85 at the first subdivision and 159 at the
second. Nevertheless valences are almost regular as
vertex valences are five, six or seven.
Figure 18: Two subdivisions of the grey face with the
incremental algorithm.
GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS
138
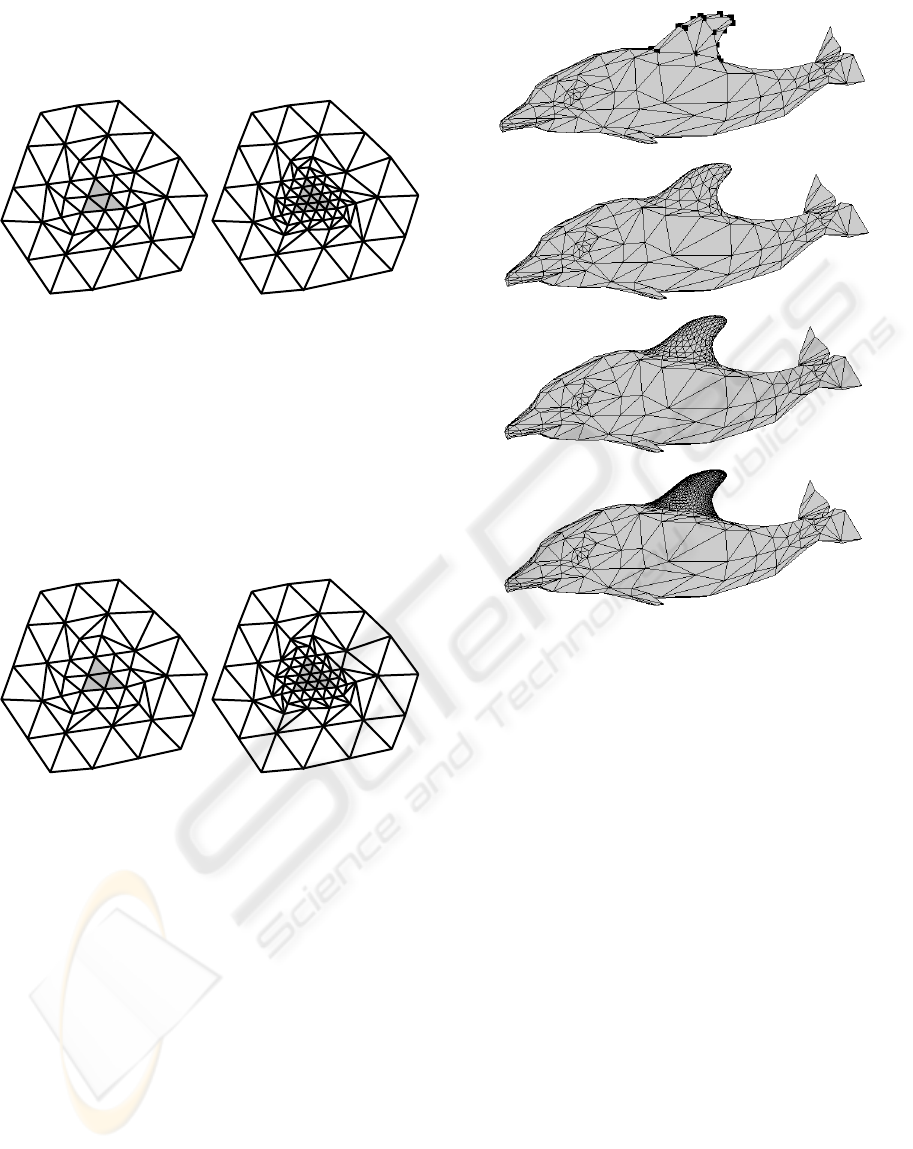
The diagonal algorithm gives an intermediate
number of faces: 67 at the first level and 121 at the
second level as shown in Figure 19.
Figure 19: Twice subdivision of the grey face with the
diagonal algorithm.
Like incremental algorithm, valences are almost
regular: six or seven. Moreover the subdivision
depth between faces is progressive. However, the
diagonal of the trapezium (during trisection) gives a
spiral appearance. To improve this, we can take one
diagonal of the trapezium at a subdivision level and
the other at the next subdivision level as shown in
Figure 20.
Figure 20: Two subdivisions of the grey face with a
variant of the diagonal algorithm.
4 RESULTS AND COMPARISON
In Figure 21, the selected area is the fin of the
dolphin model. Vertices from the faces to subdivide
are tagged by black squares (top). Then, the diagonal
algorithm is applied three times and resulting
meshes are represented in Figure 21.
Figure 21: From top to bottom, three adaptive subdivisions
of the selected dolphin fin.
The cat model automatically subdivided
according to the accuracy of the mesh approximation
in relation to the limit surface with the three
algorithms is shown in Figure 22. The initial cat
model consists in 224 faces (Figure 3). In
Figure 22,
the left mesh obtain with the T-algorithm has 898
faces, the incremental algorithm generates 1444
faces (center) and the diagonal algorithm produces
1226 faces (right).
On the left mesh in
Figure 22, two extraordinary
valences appear but the result is correct. Moreover
incremental algorithm and the diagonal algorithm
give similar results in number of faces.
A NEW NON-UNIFORM LOOP SCHEME
139

Figure 22: Meshes obtained respectively with the T-algorithm, the incremental algorithm and the diagonal algorithm.
We now compare results of the three algorithms
on a bigger mesh. The initial bunny mesh has 592
faces and we choose a smaller accuracy. In
Figure 23,
meshes are represented as follows. From top to
bottom and from left to right: the initial mesh, the T-
algorithm mesh, the incremental algorithm mesh and
the mesh generated by the diagonal algorithm. The
T-algorithm still gives the smaller mesh with 3094
faces but degenerated valences appear. For the
second time, incremental algorithm and the diagonal
algorithm give correct meshes but this time, the
incremental algorithm creates 5426 faces whereas
the diagonal algorithm generates 4282 faces.
Figure 23: Initial mesh and meshes obtained respectively
with the T-algorithm, the incremental algorithm and the
diagonal algorithm.
5 CONCLUSION
In uniform schemes, the subdivision rules are the
same for the whole input model. As there is often no
need to subdivide the whole mesh, non-uniform
subdivision is used such as the T-algorithm or the
incremental algorithm. The algorithm we introduced
in this paper takes advantages of both the T-
algorithm and the incremental algorithm. It refines
selected areas which are chosen manually or
automatically according to the accuracy of the
control mesh compared to the limit surface.
Subdivision rules avoid cracks and generate a
progressive mesh with at most one subdivision level
between two adjacent faces and proper connectivity.
Moreover valences remain regular on most of the
vertices.
REFERENCES
Amresh A., Farin G. and Razdan A., Adaptive subdivision
schemes for triangular meshes, in Hierarchical and
Geometric Methods in Scientific Visualization, H.H.
G. Farin, and B. Hamann, editors, Editor. 2003. p.
319-327.
Catmull E. and Clark J., Recursively generated B-spline
surfaces on arbitrary topological meshes. Computer
Aided Design, 1978. 9(6): p. 350-355.
Chaikin G. (1974). "An algorithm for High Speed Curve
Generation." CGIP 3, p. 346 - 349.
Doo D. and Sabin M., Behaviour of recursive subdivision
surfaces near extraordinary points. Computer Aided
Design, 1978. 9(6): p. 356-360.
Dyn N., Levin D., and Gregory J.A., A butterfly
subdivision scheme for surface interpolation with
tension control. ACM Transactions on Graphics, 1990.
9: p. 160-169.
Dyn N., Hormann K., Kim S. and Levin D. (2000).
"Optimizing 3D triangulations using discrete curvature
analysis, Oslo." Mathematical Methods for Curves and
Surfaces, p. 135-146.
Isenberg T., Hartmann K. and König H., Interest value
driven adaptive subdivision. In T. Schulze, S.
GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS
140

Schlechtweg, and V. Hinz, editors, Simulation und
Visualisierung, pages 139–149. SCS European
Publishing House, March 2003.
Lanquetin S., Etude des surfaces de subdivision :
intersection, précision et profondeur de subdivision.
PhD thesis, University of Burgundy, France, 2004.
Lanquetin S. and Neveu M., A priori computation of the
number of surface subdivision levels.Proceedings of
Computer Graphics and Vision (GRAPHICON 2004),
pp. 87-94, September 6-8, 2004, Moscow, Russia.
Loop C., Smooth Subdivision Surfaces Based on
Triangles. Department of Mathematics: Master's
thesis, University of Utah, 1987.
Meyer M., Desbrun M., Schröder P., and Barr A., Discrete
differential-geometry operators for triangulated 2-
manifolds. VisMath, 2002.
Müller K. and Havemann S., Subdivision Surface
Tesselation on the Fly using a Versatile Mesh data
Structure. Eurographics'2000, 2000. 19(3): p. 151-159.
O'Brien, D.A. and D. Manocha, Calculating Intersection
Curve Approximations for Subdivision Surfaces.
2000.
Pakdel H. and Samavati F., Incremental adaptive Loop
subdivision. ICCSA 2004, LNCS 3045, pp. 237-246,
2004.
Seeger S., Hormann K., Häusler G., and Greiner G., A
sub-atomic subdivision approach. In T. Ertl, B. Girod,
G. Greiner, H. Niemann, and H. P. Seidel, editors,
Proceedings of the Vision Modeling and Visualization
Conference 2001 (VMV-01), pages 77–86, Berlin,
November 2001. Aka GmbH.
Xu Z. and Kondo K. (1999). "Adaptive renements in
subdivision surfaces." Eurographics '99, Short papers
and demos, p. 239-242.
Zorin D., Schröder P., and Sweldens W., Interactive
multiresolution mesh editing. SIGGRAPH'98
Proceedings, 1998: p. 259-268.
A NEW NON-UNIFORM LOOP SCHEME
141
