
COMBINING METAHEURISTICS FOR THE JOB SHOP
SCHEDULING PROBLEM WITH SEQUENCE DEPENDENT SETUP
TIMES
Miguel A. Gonz
´
alez, Mar
´
ıa R. Sierra, Camino R. Vela, Ramiro Varela, Jorge Puente
Artificial Intelligence Center, Dept. of Computing, University of Oviedo,
Campus de Viesques, 33271 Gij
´
on, Spain
Keywords:
Metaheuristics, Genetic Algorithms, Local Search, Job Shop Scheduling.
Abstract:
The Job Shop Scheduling (J SS) is a hard problem that has interested to researchers in various fields such
as Operations Research and Artificial Intelligence during the last decades. Due to its high complexity, only
small instances can be solved by exact methods, while instances with a size of practical interest should be
solved by means of approximate methods guided by heuristic knowledge. In this paper we confront the Job
Shop Scheduling with Sequence Dependent Setup Times (SDJSS). The SDJSS problem models many
real situations better than the JSS. Our approach consists in extending a genetic algorithm and a local search
method that demonstrated to be efficient in solving the JSS problem. We report results from an experimental
study showing that the proposed approaches are more efficient than other genetic algorithm proposed in the
literature, and that it is quite competitive with some of the state-of-the-art approaches.
1 INTRODUCTION
The Job Shop Scheduling Problem with Sequence De-
pendent Setup Times (SDJSS) is a variant of the
classic Job Shop Scheduling Problem (JSS) in which
a setup operation on a machine is required when the
machine switches between two jobs. This way the
SDJSS models many real situations better than the
JSS. The SDJSS has interested to a number of re-
searchers, so we can find a number of approaches in
the literature, many of which try to extend solutions
that were successful to the classic JSS problem. This
is the case, for example, of the branch and bound al-
gorithm proposed by Brucker and Thiele in (Brucker
and Thiele, 1996), which is an extension of the well-
known algorithms proposed in (Brucker et al., 1994),
(Brucker, 2004) and (Carlier and Pinson, 1994), and
the genetic algorithm proposed by Cheung and Zhou
in (Cheung and Zhou, 2001), which is also an ex-
tension of a genetic algorithm for the JSS. Also,
in (Zoghby et al., 2005) a neighborhood search with
heuristic repairing is proposed that it is an extension
of the local search methods for the JSS.
In this paper we apply a similar methodological
approach and extend a genetic algorithm and a local
search method that we have applied previously to the
JSS problem. The genetic algorithm was designed
by combining ideas taken from the literature such
as for example the well-known G&T algorithm pro-
posed by Giffler and Thomson in (Giffler and Thom-
son, 1960), the codification schema proposed by Bier-
wirth in (Bierwirth, 1995) and the local search meth-
ods developed by various researchers, for example
Dell’ Amico and Trubian in (Dell’ Amico and Tru-
bian, 1993), Nowicki and Smutnicki in (Nowicki and
Smutnicki, 1996) or Mattfeld in (Mattfeld, 1995). In
(Gonz
´
alez et al., 2006) we reported results from an
experimental study over a set of selected problems
showing that the genetic algorithm is quite competi-
tive with the most efficient methods for the JSS prob-
lem.
In order to extend the algorithm to the SDJSS
problem, we have firstly extended the decoding al-
gorithm, which is based on the G&T algorithm.
Furthermore, in our local search method, we have
adapted the neighborhood structure termed N
1
in
the literature to obtain a neighborhood that we have
termed N
S
1
.
The experimental study was conducted over the
set of 45 problem instances proposed by Cheung and
Zhou in (Cheung and Zhou, 2001) and also over the
set of 15 instances proposed by Brucker and Thiele
in (Brucker and Thiele, 1996). We have evaluated the
genetic algorithm alone and then in conjunction with
211
A. González M., R. Sierra M., R. Vela C., Varela R. and Puente J. (2006).
COMBINING METAHEURISTICS FOR THE JOB SHOP SCHEDULING PROBLEM WITH SEQUENCE DEPENDENT SETUP TIMES.
In Proceedings of the First International Conference on Software and Data Technologies, pages 211-218
DOI: 10.5220/0001312402110218
Copyright
c
SciTePress
local search. The results show that the proposed ge-
netic algorithm is more efficient than the genetic al-
gorithm proposed in (Cheung and Zhou, 2001) and
that the genetic algorithm combined with local search
improves with respect to the raw genetic algorithm
when both of them run during similar amount of time.
Moreover, the efficiency of the genetic algorithm is
at least comparable to the exact approaches proposed
in (Brucker and Thiele, 1996) and (Artigues et al.,
2004).
The rest of the paper is organized as it follows.
In section 2 we formulate the SDJSS problem. In
section 3 we outline the genetic algorithm for the
SDJSS. In section 4 we describe the extended lo-
cal search method. Section 5 reports results from the
experimental study. Finally, in section 6 we summa-
rize the main conclusions.
2 PROBLEM FORMULATION
We start by defining the JSS problem. The clas-
sic JSS problem requires scheduling a set of N jobs
J
1
, . . . , J
N
on a set of M physical resources or ma-
chines R
1
, . . . , R
M
. Each job J
i
consists of a set of
tasks or operations {θ
i1
, . . . , θ
iM
} to be sequentially
scheduled. Each task θ
il
having a single resource re-
quirement, a fixed duration pθ
il
and a start time stθ
il
whose value should be determined.
The JSS has two binary constraints: precedence
constraints and capacity constraints. Precedence con-
straints, defined by the sequential routings of the tasks
within a job, translate into linear inequalities of the
type: stθ
il
+ pθ
il
≤ stθ
i(l+1)
(i.e. θ
il
before θ
i(l+1)
).
Capacity constraints that restrict the use of each re-
source to only one task at a time translate into dis-
junctive constraints of the form: stθ
il
+pθ
il
≤ stθ
jk
∨
stθ
jk
+ pθ
jk
≤ stθ
il
. Where θ
il
and θ
jk
are opera-
tions requiring the same machine. The objective is to
come up with a feasible schedule such that the com-
pletion time, i.e. the makespan, is minimized.
In the sequel a problem instance will be represented
by a directed graph G = (V, A ∪ E). Each node in
the set V represents a operation of the problem, with
the exception of the dummy nodes start and end,
which represent operations with processing time 0.
The arcs of the set A are called conjunctive arcs and
represent precedence constraints and the arcs of set
E are called disjunctive arcs and represent capacity
constraints. Set E is partitioned into subsets E
i
with
E = ∪
i=1,...,M
E
i
. Subset E
i
corresponds to resource
R
i
and includes an arc (v, w) for each pair of oper-
ations requiring that resource. The arcs are weighed
with the processing time of the operation at the source
node. The dummy operation start is connected to the
first operation of each job; and the last operation of
θ
θ
θ
θ
θ
θ
θ
θ
θ
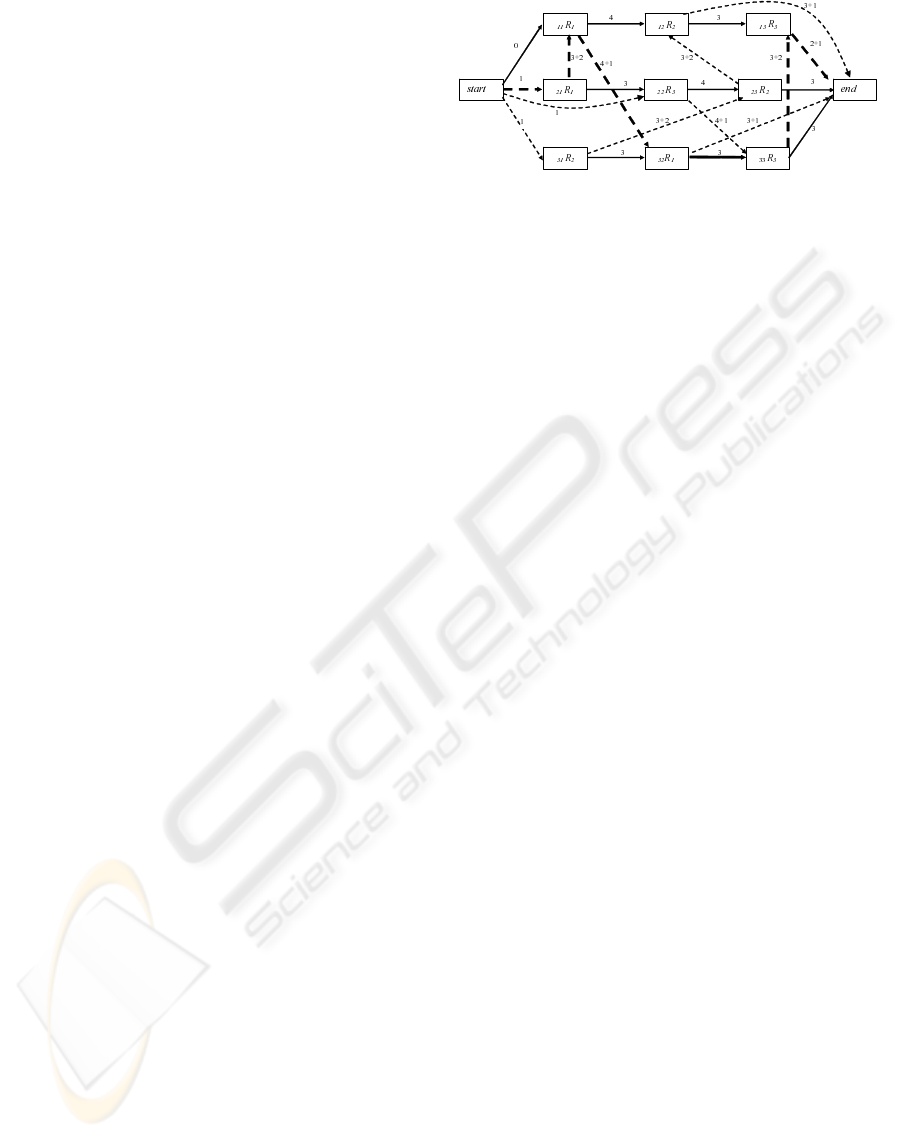
Figure 1: A feasible schedule to a problem with 3 jobs and 3
machines. Bold face arcs show a critical path whose length,
i.e. the makespan, is 22.
each job is connected to the node end.
A feasible schedule is represented by an acyclic
subgraph G
s
of G, G
s
= (V, A ∪ H), where H =
∪
i=1..M
H
i
, H
i
being a hamiltonian selection of E
i
.
Therefore, finding out a solution can be reduced to
discovering compatible hamiltonian selections, i.e.
orderings for the operations requiring the same re-
source or partial schedules, that translate into a solu-
tion graph G
s
without cycles. The makespan of the
schedule is the cost of a critical path. A critical path
is a longest path from node start to node end. The crit-
ical path is naturally decomposed into subsequences
B
1
, . . . , B
r
called critical blocks. A critical block
is a maximal subsequence of operations of a critical
path requiring the same machine.
In the SDJSS, after an operation v of a job leaves
machine m and before entering an operation w of an-
other job on the same machine, a setup operation is
required with duration S
m
v w
. The setup operation can
be started as soon as operation v leaves the machine
m, hence possibly in parallel with the operation pre-
ceding w in its job sequence. The setup time S
m
v w
is
added to the processing time of operation v to obtain
the cost of each disjunctive arc (v, w). S
m
0v
is the setup
time of machine m if v is the first operation scheduled
on m and S
m
v0
is the cleaning time of machine m if v
is the last operation scheduled on m.
Figure 1 shows a feasible solution to a problem
with 3 jobs and 3 machines. Dotted arcs represent the
elements of set E included in the solution, while con-
junctive arcs are represented by continuous arrows.
3 GENETIC ALGORITHM FOR
THE SDJSS PROBLEM
The JSS is a paradigm of constraint satisfac-
tion problems and was confronted by many heuris-
tic techniques. In particular genetic algorithms
(Bierwirth, 1995),(Mattfeld, 1995),(Varela et al.,
2003),(Gonz
´
alez et al., 2006) are a promising ap-
proach due to their ability to be combined with other
ICSOFT 2006 - INTERNATIONAL CONFERENCE ON SOFTWARE AND DATA TECHNOLOGIES
212

Algorithm 1 Conventional Genetic Algorithm.
input: a JSS problem P
output: a schedule H for problem P
1. Generate the Initial Population;
2. Evaluate the Population;
while No termination criterion is satisfied do
3. Select chromosomes from the current popula-
tion;
4. Apply the Crossover and Mutation operators
to the chromosomes selected at step 3. to gener-
ate new ones;
5. Evaluate the chromosomes generated at step
4;
6. Apply the Acceptation criterion to the set of
chromosomes selected at step 3. together with
the chromosomes generated at step 4.;
end while
7. Return the schedule from the best chromosome
evaluated so far;
techniques such as tabu search and simulated anneal-
ing. Moreover genetic algorithms allow for exploit-
ing any kind of heuristic knowledge from the problem
domain. In doing so, genetic algorithms are actually
competitive with the most efficient methods for JSS.
As mentioned above, in this paper we consider a
conventional genetic algorithm for tackling the JSS
and extend it to the SDJSS. This requires mainly the
adaptation of the decoding algorithm. Additionally
we consider a local search method for the JSS and
adapt it to the SDJSS.
Algorithm 1 shows the structure of the genetic al-
gorithm we have considered. In the first step the ini-
tial population is generated and evaluated. Then the
genetic algorithm iterates over a number of steps or
generations. In each iteration a new generation is built
from the previous one by applying the genetic opera-
tors of selection, crossover, mutation and acceptation.
In principle, these four operators can be implemented
in a variety of ways and are independent each one to
the others. However in practice all of them should
be chosen considering their effect on the remaining
ones in order to get a successful convergence. The
approach taken in this work is the following. In the se-
lection phase all chromosomes are grouped into pairs,
and then each one of these pairs is mated and mutated
accordingly to the corresponding probabilities to ob-
tain two offsprings. Finally a tournament selection is
done among each pair of parents and their offsprings.
To codify chromosomes we have chosen permu-
tations with repetition proposed by C. Bierwirth in
(Bierwirth, 1995). In this scheme a chromosome
is a permutation of the set of operations, each one
being represented by its job number. This way a
job number appears within a chromosome as many
times as the number of operations of its job. For
example, the chromosome (2 1 1 3 2 3 1 2 3)
actually represents the permutation of operations
(θ
21
θ
11
θ
12
θ
31
θ
22
θ
32
θ
13
θ
23
θ
33
). This permutation
should be understood as expressing partial schedules
for every set of operations requiring the same ma-
chine. This codification presents a number of inter-
esting characteristics; for example, it is easy to eval-
uate with different algorithms and allows for efficient
genetic operators. In (Varela et al., 2005) this cod-
ification is compared with other permutation based
codifications and demonstrated to be the best one for
the JSS problem over a set of 12 selected problem
instances of common use. For chromosome mating
we have considered the Generalized Order Crossover
(GOX) that works as it is shown in the following ex-
ample. Let us consider that the two following chro-
mosomes are selected as parents for crossover
Parent1 (1 2 3 3 2 1 1
3 2) Parent2 (3 3 2 3 1 1 2 2 1)
Firstly, a substring is selected from Parent1 and in-
serted in the Offspring at the same position as in this
parent. Then the remaining positions of the Offspring
are completed with genes from Parent2 after having
removed the genes selected from Parent1. If the se-
lected substring from Parent1 is the one marked with
underlined characters, the resulting Offspring is
Offspring (3 2 3 3 2 1 1 1 2).
By doing so, GOX preserves the order and posi-
tion of the selected substring from Parent1 and the
relative order of the remaining genes from Parent2.
The mutation operator simply selects and swaps two
genes at random. In practice the mutation would not
actually be necessary due to the GOX operator has
an implicit mutation effect. For example the second 3
from Parent1 is now the third one in the Offspring.
3.1 Decoding Algorithm
As decoding algorithm we have chosen the well-
known G&T algorithm proposed by Giffler and
Thomson in (Giffler and Thomson, 1960) for the JSS
and then we have made a natural extension for the
SDJSS. The G&T algorithm is an active schedule
builder. A schedule is active if one operation must
be delayed when you want another one to start ear-
lier. Active schedules are good in average and, what
is most important, it can be proved that the space of
active schedules contains at least an optimal one, that
is, the set of active schedules is dominant. For these
reasons it is worth to restrict the search to this space.
Moreover, the G&T algorithm is complete for the
JSS problem. Algorithm 2 shows the G&T algo-
rithm for the JSS.
In order to adapt the G&T algorithm for the
SDJSS we consider an extension termed EG&T .
COMBINING METAHEURISTICS FOR THE JOB SHOP SCHEDULING PROBLEM WITH SEQUENCE
DEPENDENT SETUP TIMES
213

Algorithm 2 The decoding Giffler and Thomson al-
gorithm for the JSS problem .
input: a chromosome C and a problem P
output: the schedule H represented by chromo-
some C for problem P
1. A = set containing the first operation of each job;
while A 6= ∅ do
2. Determine the operation θ
′
∈ A with the ear-
liest completion time if scheduled in the current
state, that is stθ
′
+ pθ
′
≤ stθ + pθ, ∀θ ∈ A;
3. Let R be the machine required by θ
′
, and B
the subset of A whose operations require R;
4. Remove from B every operation that cannot
start at a time earlier than stθ
′
+ pθ
′
;
5. Select θ
∗
∈ B so that it is the leftmost opera-
tion of B in the chromosome sequence;
6. Schedule θ
∗
as early as possible to build the
partial schedule corresponding to the next state;
7. Remove θ
∗
from A and insert the succeed-
ing operation of θ
∗
in set A if θ
∗
is not the last
operation of its job;
end while
8. return the built schedule;
EG&T can be derived from the algorithm EGT A1
developed by Ovacik and Uzsoy in (Ovacik and Uz-
soy, 1993), by simply taking into account the setup
times in Algorithm 2. So, the step 4 of Algorithm 2 is
exchanged by
4. Remove from B every operation θ that stθ ≥
stθ
′
+ pθ
′
+ S
R
θ
′
θ
for any θ
′
∈ B;
In Algorithm 2, stθ refers to the maximum comple-
tion time of the last scheduled operation on the ma-
chine required by operation θ and the preceding op-
eration to θ in its job. Hence the algorithm can be
adapted to the SDJSS problem by considering stθ
as the maximum completion time of the preceding
operation in the job and the completion time of the
last scheduled operation in the machine plus the cor-
responding setup time. It is easy to demonstrate that
EG&T is not complete. In (Artigues et al., 2005)
two more extensions of the G&T schedule genera-
tion scheme are proposed, one of them is not com-
plete either, and the other is complete but it is very
time consuming due to it needs to do backtracking.
In any case, the lack of completeness of a decoding
algorithm is not a serious problem in the framework
of GAs due to a GA itself is not complete. More-
over, the local search schema outlined in the next sec-
tion gives to any chromosome the chance of being
reached, so in any way the lack of completeness of
the decoding algorithm is compensated.
Algorithm 3 The Local Search Algorithm.
input: a chromosome C and a JSS problem P
output: a (hopefully) improved chromosome
1. Evaluate chromosome C (Algorithm 2) to obtain
schedule H;
while No termination criterion is satisfied do
2. Generate the neighborhood of H with some
method N, N(H);
3. Select H
′
∈ N (H) with the selection crite-
rion;
4. Replace H by H
′
if the acceptation criterion
holds;
end while
5. Rebuild chromosome C from schedule H;
6. return chromosome C;
4 LOCAL SEARCH
Conventional genetic algorithms, like the one de-
scribed in the previous section, often produce moder-
ate results. However meaningful improvements can
be obtained by means of hybridization with other
methods. One of such techniques is local search, in
this case the genetic algorithm is called a memetic al-
gorithm. Hybridization of a genetic algorithm with
local search is carried out by applying the local search
algorithm to every chromosome just after this chro-
mosome is generated, instead of simply applying the
Algorithm 2 as it is done in the simple genetic algo-
rithm. Algorithm 3 shows the typical strategy of a
local search.
Roughly speaking local search is implemented by
defining a neighborhood of each point in the search
space as the set of chromosomes reachable by a given
transformation rule. Then a chromosome is replaced
in the population by one of its neighbors, if any of
them satisfies the acceptation criterion. The local
search from a given point completes either after a
number of iterations or when no neighbor satisfies the
acceptation criterion.
In this paper we consider the neighborhood struc-
ture proposed by Nowicki and Smutnicki in (Now-
icki and Smutnicki, 1996), which is termed N
1
by D.
Mattfeld in (Mattfeld, 1995), for the JSS. As other
strategies, N
1
relies on the concepts of critical path
and critical block. It considers every critical block of
a critical path and made a number of moves on the op-
erations of each block. After a move inside a block,
the feasibility must be tested. Since an exact proce-
dure is computationally prohibitive, the feasibility is
estimated by an approximate algorithm proposed by
Dell’ Amico and Trubian in (Dell’ Amico and Tru-
bian, 1993). This estimation ensures feasibility at the
expense of omitting a few feasible solutions. In (Mat-
tfeld, 1995) the transformation rules of N
1
are defined
ICSOFT 2006 - INTERNATIONAL CONFERENCE ON SOFTWARE AND DATA TECHNOLOGIES
214

as follows.
Definition 1 (N
1
) Given a schedule H with partial
schedules H
i
for each machine R
i
, 1 ≤ i ≤ M, the
neighborhood N
1
(H) consist of all schedules derived
from H by reversing one arc (v, w) of the critical path
with (v, w) ∈ H
i
. At least one of v and w is either
the first or the last member of a block. For the first
block only v and w at the end of the block are con-
sidered whereas for the last block only v and w at the
beginning of the block must be checked.
The selection strategy of a neighbor and the ac-
ceptation criterion are based on a makespan estima-
tion, which is done in constant time as it is also de-
scribed in (Dell’ Amico and Trubian, 1993), instead
of calculating the exact makespan of each neigh-
bor. The estimation provides a lower bound of the
makespan. The selected neighbor is the one with
the lowest makespan estimation whenever this value
is lower than the makespan of the current chromo-
some. Notice that this strategy is not steepest descen-
dent because the exact makespan of selected neigh-
bor is not always better than the makespan of the
current solution. We have done this choice in the clas-
sic JSS problem due to it produces better results than
a strict steepest descent gradient method. (Gonz
´
alez
et al., 2006).
The Algorithm stops either after a number of iter-
ations or when the estimated makespan of selected
neighbor is larger than the makespan of the current
chromosome.
This neighborhood relies on the fact that, for the
JSS problem, reversing an arc of the critical path al-
ways maintains feasibility. Moreover, the only possi-
bility to obtain some improvement by reversing an arc
is that the reversed arc is either the first or the last of
a critical block.
However, things are not the same for SDJSS
problem due to the differences in the setup times. As
can we see in (Zoghby et al., 2005), feasibility is not
guaranteed when reversing an arc of the critical path,
and reversing an arc inside a block could lead to an
improving schedule. The following results give suf-
ficient conditions of no-improving when an arc is re-
versed in a solution H of the SDJSS problem. In
the setup times the machine is omitted for simplicity
due to all of them refers to the same machine.
Theorem 1 Let H be a schedule and (v, w ) an arc
that is not in a critical block. Then reversing the arc
(v, w) does not produce any improvement even if the
resulting schedule is feasible.
Theorem 2 Let H be a schedule and (v, w) an arc in-
side a critical block, that is there exist arcs (x, v) and
(w, y) belonging to the same block. Even if the sched-
ule H
′
obtained from H by reversing the arc (v, w) is
feasible, H
′
is not better than H if the following con-
dition holds
S
xw
+ S
wv
+ S
v y
≥ S
xv
+ S
v w
+ S
wy
(1)
Theorem 3 Let H be a schedule and (v, w ) an arc
in a critical path so that v is the first operation of the
first critical block and z is the successor of w in the
critical path and M
w
= M
z
. Even if reversing the
arc (v, w) leaves to a feasible schedule, there is no
improvement if the following condition holds
S
0w
+ S
wv
+ S
v z
≥ S
0v
+ S
v w
+ S
wz
(2)
Analogous, we can formulate a similar result if w is
the last operation of the last critical block.
Hence we can finally define the neighborhood strat-
egy for the SDJSS problem as it follows
Definition 2 (N
S
1
) Given a schedule H, the neigh-
borhood N
S
1
(H) consist of all schedules derived from
H by reversing one arc (v, w) of the critical path pro-
vided that none of the conditions given in previous
theorems 1, 2 and 3 hold.
4.1 Feasibility Checking
Regarding feasibility, for the SDJSS it is always re-
quired to check it after reversing an arc. As usual, we
assume that the triangular inequality holds, what is
quite reasonable in actual production plans, that is for
any operations u,v and w requiring the same machine
S
uw
≤ S
uv
+ S
v w
(3)
Then the following is a necessary condition for no-
feasibility after reversing the arc (v, w).
Theorem 4 Let H be a schedule and (v, w) an arc in
a critical path, P J
w
the operation preceding w in its
job and SJ
v
the successor of v in its job. Then if re-
versing the arc (v, w) produces a cycle in the solution
graph, the following condition holds
stP J
w
> stSJ
v
+ duSJ
v
+ S
min
(4)
where
S
min
= min{S
kl
/(k, l) ∈ E, J
k
= J
v
}
and J
k
is the job of operation k.
Therefore the feasibility estimation is efficient at
the cost of discarding some feasible neighbor.
4.2 Makespan Estimation
For makespan estimation after reversing an arc, we
have also extended the method proposed by Taillard in
(Taillard, 1993) for the JSS. This method was used
also by Dell’Amico and Trubian in (Dell’ Amico and
Trubian, 1993) and by Mattfeld in (Mattfeld, 1995).
COMBINING METAHEURISTICS FOR THE JOB SHOP SCHEDULING PROBLEM WITH SEQUENCE
DEPENDENT SETUP TIMES
215

This method requires calculating heads and tails. The
head r
v
of an operation v is the cost of the longest
path from node start to node v in the solution graph,
i.e. is the value of stv. The tail q
v
is defined so as the
value q
v
+p
v
is the cost of the longest path from node
v to node end.
For every node v, the value r
v
+ p
v
+ q
v
is the
length of the longest path from node start to node end
trough node v, and hence it is a lower bound of the
makespan. Moreover, it is the makespan if node
v belongs to the critical path. So, we can get a lower
bound of the new schedule by calculating r
v
+p
v
+q
v
after reversing (v, w).
Let us denote by P M
v
and SM
v
the predecessor
and successor nodes of v respectively on the machine
sequence in a schedule. Let nodes x and z be PM
v
and SM
w
respectively in schedule H. Let us note that
in H
′
nodes x and z are P M
w
and SM
v
respectively.
Then the new heads and tails of operations v and w
after reversing the arc (v, w) can be calculated as the
following
r
′
w
= max(r
x
+ px + S
xw
, r
P J
w
+ pP J
w
)
r
′
v
= max(r
′
w
+ pw + S
wv
, r
P J
v
+ pP J
v
)
q
′
v
= max(q
z
+ pz + S
v z
, q
SJ
v
+ pSJ
v
)
q
′
w
= max(q
′
v
+ pv + S
v w
, q
SJ
w
+ pSJ
w
)
From these new values of heads and tails the
makespan of H
′
can be estimated by
C
′
max
= max(r
′
v
+ pv + q
′
v
, r
′
w
+ pw + q
′
w
)
which is actually a lower bound of the new
makespan. This way, we can get an efficient
makespan estimation of schedule H
′
at the risk of
discarding some improving schedule.
5 EXPERIMENTAL STUDY
For experimental study we have used the set of prob-
lems proposed by Cheung and Zhou in (Cheung and
Zhou, 2001) and also the benchmark instances taken
from Brucker and Thiele (Brucker and Thiele, 1996).
The first one is a set of 45 instances with sizes (given
by the number of jobs and number of machines N ×
M) 10 × 10, 10 × 20 and 20 × 20, which is organized
into 3 types. Instances of type 1 have processing times
and setup times uniformly distributed in (10,50); in-
stances of type 2 have processing times in (10,50)
and setup times in (50,99); and instances of type 3
have processing times in (50,99) and setup times in
(10,50). Table 1 shows the results from the genetic al-
gorithm termed GA
SP T S reported in (Cheung and
Zhou, 2001). The data are grouped for sizes and types
and values reported are averaged for each group. This
algorithm was coded in FORTRAN and run on PC
Table 1: Results from the GA
SP T S.
ZRD Size Type Best Avg StDev
Instance N × M
1-5 10 × 10 1 835,4 864,2 21,46
6-10 10 × 10 2 1323,0 1349,6 21,00
11-15 10 × 10 3 1524,6 1556,0 35,44
16-20 20 × 10 1 1339,4 1377,0 25,32
21-25 20 × 10 2 2327,2 2375,8 46,26
26-30 20 × 10 3 2426,6 2526,2 75,90
31-35 20 × 20 1 1787,4 1849,4 57,78
36-40 20 × 20 2 2859,4 2982,0 93,92
41-45 20 × 20 3 3197,8 3309,6 121,52
Table 2: Results from the GA EG&T .
ZRD Size Type Best Avg StDev
Instances N × M
1-5 10 × 10 1 785,0 803,0 8,76
6-10 10 × 10 2 1282,0 1300,2 9,82
11-15 10 × 10 3 1434,6 1455,4 12,87
16-20 20 × 10 1 1285,8 1323,0 15,38
21-25 20 × 10 2 2229,6 2278,2 22,24
26-30 20 × 10 3 2330,4 2385,8 23,91
31-35 20 × 20 1 1631,6 1680,4 17,99
36-40 20 × 20 2 2678,0 2727,8 23,60
41-45 20 × 20 3 3052,0 3119,6 29,33
Table 3: Results from the GA EG&T LS.
ZRD Size Type Best Avg StDev
Instances N × M
1-5 10 × 10 1 778,6 788,5 6,70
6-10 10 × 10 2 1270,0 1290,4 9,16
11-15 10 × 10 3 1433,8 1439,8 6,71
16-20 20 × 10 1 1230,2 1255,5 12,74
21-25 20 × 10 2 2178,4 2216,8 18,61
26-30 20 × 10 3 2235,2 2274,0 19,32
31-35 20 × 20 1 1590,0 1619,8 15,90
36-40 20 × 20 2 2610,2 2668,0 27,48
41-45 20 × 20 3 2926,0 2982,2 26,32
486/66. The computation time with problem sizes
10 × 10, 10 × 20 and 20 × 20 are about 16, 30 and 70
minutes respectively. Each algorithm run was stopped
at the end of the 2000th generation and tried 10 times
for each instance.
Tables 2 and 3 reports the results reached by
the genetic algorithm alone and the genetic algo-
rithm with local search, termed GA
EG&T and
GA
EG&T LS respectively, proposed in this work.
In the first case the genetic algorithm was parameter-
ized with a population of 100 chromosomes, a num-
ber of 140 generations, crossover probability of 0.7,
ICSOFT 2006 - INTERNATIONAL CONFERENCE ON SOFTWARE AND DATA TECHNOLOGIES
216

0.99
1
1.01
1.02
1.03
1.04
1.05
1.06
1.07
0 5 10 15 20 25 30 35 40 45
GA_EG&T / GA_EG&T_LS
Figure 2: Comparison of the raw genetic algorithm with
the memetic algorithm. The graphic shows for each prob-
lem the quotient of the mean makespan of the best solutions
reached in all 30 trials by the raw GA and the GA with local
search.
and mutation probability of 0.2. For the experiments
combining the genetic algorithm with local search,
we have parameterized the genetic algorithms with 50
chromosomes in the population and 50 generations in
order to have similar running times.
The rest of the parameters remain as in previous
experiments. The genetic algorithm was run 30 times
and reported the values of the best solution reached,
the average of the best solutions of the 30 runs and the
standard deviation. The machine was a Pentium IV at
1.7 Ghz. and the computation time varied from about
1 sec. for the smaller instances to about 10 sec. for the
larger ones. As we can observe both algorithms im-
proved the results obtained by the GA
SP T S. More-
over algorithm GA
EG&T LS has outperformed
GA
EG&T . Figure 2 shows the relative improve-
ment of GA
EG&T LS over GA EG&T in all
problems. The improvement is clear in almost all
cases.
Regarding the benchmark from Brucker and Thiele
(Brucker and Thiele, 1996), these instances are de-
fined from the classical JSS instances, proposed by
Lawrence (Lawrence, 1984), by introducing setup
times. There are 15 instances named t2
ps01 to
t2
ps15. Instances t2 ps01 to t2 ps05 are of type
10×5 (small instances). Instances t2
ps06 to t2 ps10
are of type 15 × 5 (medium instances). Instances
t2 ps11 to t2 ps15 are of type 20×5 (large instances).
Table 4 shows results from two state-of-the-art meth-
ods: the branch and bound algorithms proposed by
Brucker and Thiele (Brucker and Thiele, 1996) (de-
noted as BT 96) and Artigues et al. in (Artigues et al.,
2004) (denoted as ABF 04). In the results reported
in (Brucker and Thiele, 1996) and (Artigues et al.,
2004) the target machine was Sun 4/20 station and
Pentium IV at 2.0 GHz. in both cases the time limit
for the experiments was 7200 sec. In this case, our
Table 4: Comparison between BT 96, ABF 04 and
GA
EG&T LS.
Problem Size BT 96 ABF 04 GA EG&T LS
Instance N × M
t2 ps01 10 × 5 798 798 798
t2
ps02 10 × 5 784 784 784
t2
ps03 10 × 5 749 749 749
t2
ps04 10 × 5 730 730 730
t2
ps05 10 × 5 691 691 693
t2 ps06 15 × 5 1056 1026 1026
t2
ps07 15 × 5 1087 970 970
t2
ps08 15 × 5 1096 1002 975
t2
ps09 15 × 5 1119 1060 1060
t2
ps05 15 × 5 1058 1018 1018
t2 ps06 20 × 5 1658 - 1450
t2
ps07 20 × 5 1528 1319 1347
t2
ps08 20 × 5 1549 1439 1431
t2
ps09 20 × 5 1592 - 1532
t2
ps05 20 × 5 1744 - 1523
values in bold are optimal
memetic algorithm was parameterized as the follow-
ing: population size = 100 for small and medium in-
stances and 200 for larger instances, and the number
of generations has been 100 for small instances, 200
for medium instances, and 400 for larger instances.
The rest of the parameters remain as in previous ex-
periments. We run the algorithm 30 times for each
instance, and the computation time for the larger in-
stances was 30 sec. for each run, i.e. 900 sec. of
running time for each instance.
As we can observe, GA
EG&T LS is able to
reach optimal solutions for the smaller instances, as
BT 96 and ABF 04, with only one exception. For
the medium and large instances reaches solutions that
are better or equal than ABF 04 and much better that
BT 06. Unfortunately, for the larger instances, re-
sults from only two instances are reported in (Artigues
et al., 2004).
6 CONCLUSION
In this work we have confronted the Job Shop
Scheduling Problem with Sequence Dependent Setup
Times by means of a genetic algorithm hybridized
with local search. As other approaches reported in
the literature, we have extended a solution developed
for the classic JSS problem. We have reported re-
sults from an experimental study on the benchmark
proposed in (Cheung and Zhou, 2001) showing that
the proposed genetic algorithms produce better results
than the genetic algorithm proposed in (Cheung and
Zhou, 2001), mainly when these algorithms are hy-
COMBINING METAHEURISTICS FOR THE JOB SHOP SCHEDULING PROBLEM WITH SEQUENCE
DEPENDENT SETUP TIMES
217

bridized with local search. Here it is important to re-
mark that the running conditions of both genetic algo-
rithms are not strictly comparable. Also we have ex-
perimented with the benchmark proposed by Brucker
and Thiele in (Brucker and Thiele, 1996), and com-
pare our memetic algorithm with two state-of-the-art
exact branch and bound approaches due to Brucker
and Thiele (Brucker and Thiele, 1996) and Artigues
et al. in (Artigues et al., 2004) respectively. In this
case the results shown that our approach is quite com-
petitive.
As future work we plan to look for new exten-
sions of the G&T algorithm in order to obtain a com-
plete decoding algorithm and more efficient opera-
tors. Also we will try to extend other local search
algorithms and neighborhoods that have been proved
to be very efficient for the JSS problem.
ACKNOWLEDGEMENTS
We would like to thank Waiman Cheung and Hong
Zhou, and Christian Artigues for facilitating us the
benchmarks used in the experimental study. This re-
search has been supported by FEDER-MCYT under
contract TIC2003-04153 and by FICYT under grant
BP04-021.
REFERENCES
Artigues, C., Belmokhtar, S., and Feillet, D. (2004). A New
Exact Algorithm for the Job shop Problem with Se-
quence Dependent Setup Times, pages 96–109. LNCS
3011. Springer-Verlag.
Artigues, C., Lopez, P., and P.D., A. (2005). Schedule
generation schemes for the job shop problem with
sequence-dependent setup times: Dominance proper-
ties and computational analysis. Annals of Opera-
tional Research, 138:21–52.
Bierwirth, C. (1995). A generalized permutation approach
to jobshop scheduling with genetic algorithms. OR
Spectrum, 17:87–92.
Brucker, P. (2004). Scheduling Algorithms. Springer-
Verlag, 4th edition.
Brucker, P., Jurisch, B., and Sievers, B. (1994). A branch
and bound algorithm for the job-shop scheduling
problem. Discrete Applied Mathematics, 49:107–127.
Brucker, P. and Thiele, O. (1996). A branch and
bound method for the general-job shop problem with
sequence-dependent setup times. Operations Re-
search Spektrum, 18:145–161.
Carlier, J. and Pinson, E. (1994). Adjustment of heads and
tails for the job-shop problem. European Journal of
Operational Research, 78:146–161.
Cheung, W. and Zhou, H. (2001). Using genetic algorithms
and heuristics for job shop scheduling with sequence-
dependent setup times. Annals of Operational Re-
search, 107:65–81.
Dell’ Amico, M. and Trubian, M. (1993). Applying tabu
search to the job-shop scheduling problem. Annals of
Operational Research, 41:231–252.
Giffler, B. and Thomson, G. (1960). Algorithms for solving
production scheduling problems. Operations Reseach,
8:487–503.
Gonz
´
alez, M., Sierra, M., Vela, C., and Varela, R. (2006).
Genetic Algorithms Hybridized with Greedy Algo-
rithms and Local Search over the Spaces of Active and
Semi-active Schedules. LNCS (to appear). Springer-
Verlag.
Lawrence, S. (1984). Resource constrained project
scheduling: an experimental investigation of heuris-
tic scheduling techniques (supplement). Technical re-
port, Graduate School of Industrial Administration,
Carnegie Mellon University.
Mattfeld, D. (1995). Evolutionary Search and the Job Shop.
Investigations on Genetic Algorithms for Production
Scheduling. Springer-Verlag.
Nowicki, E. and Smutnicki, C. (1996). A fast taboo search
algorithm for the job shop problem. Management Sci-
ence, 42:797–813.
Ovacik, I. and Uzsoy, R. (1993). Exploiting shop floors sta-
tus information to schedule complex jobs. Operations
Research Letters, 14:251–256.
Taillard, E. (1993). Parallel taboo search techniques for the
job shop scheduling problem. ORSA Journal of Com-
puting, 6:108–117.
Varela, R., Serrano, D., and M., S. (2005). New Codifica-
tion Schemas for Scheduling with Genetic Algorithms,
pages 11–20. LNCS 3562. Springer-Verlag.
Varela, R., Vela, C., Puente, J., and A., G. (2003). A
knowledge-based evolutionary strategy for scheduling
problems with bottlenecks. European Journal of Op-
erational Research, 145:57–71.
Zoghby, J., Barnes, J., and J.J., H. (2005). Modeling the
re-entrant job shop scheduling problem with setup for
metaheuristic searches. European Journal of Opera-
tional Research, 167:336–348.
ICSOFT 2006 - INTERNATIONAL CONFERENCE ON SOFTWARE AND DATA TECHNOLOGIES
218
