
Effect of Communication Error on
“Iterated Proposal–Voting Process”
Hiroshi Kawakami, Toshiaki Tanizawa, Osamu Katai and Takayuki Shiose
Graduate School of Informatics, Kyoto University,
Yoshida-Honmachi, Kyoto 606-8501, Japan
Abstract. This paper proposes the framework of a multi-agent simulation called
“iterated proposal–voting process” and reports the effect of communication error
on the decision-making of a relatively small community. The community try to
decide on a shared rule via iteration of “propose and vote.” In this framework,
each agent decides its action based on two criteria: satisfying “physiologically
fixed needs” and satisfying “social contextual needs (SNs),” which sometimes
conflict with each other. These criteria are derived from a Nursing Theory that
puts special emphasis on the relation between subjects and others. SNs are sat-
isfied when such relations are balanced. Employing “Hyder’s theory of cognitive
balance,” SNs are evaluated for whether they are balanced. The simulation yields
some interesting phenomena that are not observed by conventional static analy-
ses, e.g. power indices.
1 Introduction
Through the process of decision-making by a community, the final decision should re-
flect all members’ preferences and beliefs, but it is difficult to arrive at such an ideal
decision because personal preferences vary with personalities, and the relations among
members are not simple [1]. Especially in relatively small communities, it is well known
that a personal decision can strongly influence the final decision, leading the so-called
“groupthink,” “risky shift [2],” and so on. Recently, multi-agent simulations have been
applied to analyze such phenomena that emerge in decision-making processes in a bot-
tom up manner, e.g. [3].
The target of our agent-based simulation is a relatively small community that tries to
decide a shared rule of community through a process that can be modeled as “iterated
proposal and voting.” One of the characteristics of our model is the mental model of
each agent based on Nursing Theory, especially the Behavioral Systems Model [4],
which focuses not only on personal preferences but also on social relationships. The
social relationships are assessed by employing Heider’s theory of cognitive balance [5].
The preference of voting of each agent is revised through the “iterated proposal and
voting” by using Q-learning [6]. Our model is applied to examine the effect of errors
on decision-making. The results of simulation are compared with those of conventional
methods of analyzing voting systems [7].
Kawakami H., Tanizawa T., Katai O. and Shiose T. (2006).
Effect of Communication Error on “Iterated Proposal–Voting Process”.
In Proceedings of the 2nd International Workshop on Multi-Agent Robotic Systems, pages 83-92
DOI: 10.5220/0001224200830092
Copyright
c
SciTePress

2 Decision Making via “Iterated Proposal–Voting Process”
Decision-making is an interesting topic for Game Theory, Social Psychology, Politics,
Sociology, etc., and many research efforts have been carried out. This paper aims to
contribute to this research field by considering the notions of “personal needs vs. social
relationship” and “iterated proposal-vote process.”
2.1 Model of Each Agent and Shared Rule
The iterated process of decision-making by a community is affected by the actions,
preferences, and beliefs of each constituent and by the relationships among them. In
order to simulate this process, the method of modeling each agent emerges as the main
issue. Recent researches has attempted to model agents based not on a simple strategy
such as “chasing optimality” but on complex and human-like strategies. For example,
some agents are defined by introducing the notion of physiology based on Transactional
Analysis, while others are defined by introducing the notion on ethics [8]. This paper
defines agents by introducing the notion of Nursing Theory, especially the Behavioral
Systems Model [9], which is derived from a tremendous number of observations of
“patterns of human behavior.” The main feature of this model is its treatment of instincts
by considering the motivation of maintaining relationships.
Although the monumental book “Notes on Nursing [10]” by F. Nightingale has not
been cited for a long time, various theories motivated by the Notes have been devel-
oped since 1950 [4]. These theories vary depending on the basic philosophy. Among
them, we employ “system theories [4]” as the basis of modeling agents. The common
standpoint of system theories is that a human being consists of several systems, which
are categorized into two groups: physiologically personal ones and social ones. For
example, the Behavioral Systems Model [9] defines the “behavior system of humans”
as an integration of seven subsystems, called “affiliative,” “dependency,” “ingestive,”
“eliminative,” “sexual,” “aggressive,” and “achievement” subsystems. Affiliative and
dependency subsystems are social while the others are personal. Hereafter, we call the
requirement derived from the former “social contextual needs (SN)” and that from the
later “physiologically fixed needs (PN).”
Each subsystem tends to satisfy its requirements and be in a balanced state. If some
subsystem of a person is imbalanced, he/she feels nonconformity and is thus motivated
to take certain actions, which lead to subsystems becoming balanced. Furthermore, sub-
systems sometimes conflict with each other. An action made to balance a subsystem
may lead to another subsystem becoming imbalanced.
Physiologically fixed Needs (PN) and Shared Rule. Physiologically fixed Needs (PN)
reflect personal and physiologically requirements, e.g., preferable temperature, bright-
ness, and calmness of a room, which are independent of relationships with other people
but sometimes conflict with the preferences of other people. Therefore, a community
needs a shared rule for governing such requirements.
84

Initial shared rule P = {4, 4, 1}
P N
0
= {4, 3, 5}
P N
1
= {1, 5, 2}
P N
2
= {5, 3, 2}
zw
Shared Rule
n0 n1 n2
Φ(a0) Φ(a1) Φ(a2)
adopt
p0 p1 p2
a0
1
proposer
1
a1
1
a2
2 1 3
Fig.1. Example of initial P , P N
i
, and “a step of proposal-vote and alteration of Φ(a
i
)”.
Shared Rule: Deciding the value of a shared rule is the objective of our simulation.
A shared rule is represented by a set of values that governs all of the members of the
community. Such a rule must be decided through discussion among all members. Our
“proposal–voting system” implements a shared rule as a list of integers:
P = {p
0
, p
1
, p
2
, · · · , p
R
l
−1
},
where R
l
denotes the number of factors that commonly affect all members, and each
factor p
j
is assigned an integer (0 ≤ p
j
< R
s
).
Coding PN: PN of each agent reflect factors of the shared rule. Therefore, each need
(n
i
j
) of an agent a
i
is represented by an integer (0 ≤ n
i
j
< R
s
), and each “PN of an
agent a
i
” is encoded into a list of needs:
P N
i
= {n
i
0
, n
i
1
, n
i
2
, ..., n
i
R
l
−1
}.
An example of a set of a shared rule (P ) and PNs is shown in the left part of fig. 1,
where R
l
= 3, R
s
= 7 and the number of agents L = 3. The right upper part of fig. 1
illustrates this situation.
Satisfaction of PN: If the difference between the value of each element of PN (n
i
j
) and
that of the shared rule (p
j
) is within the tolerance range (σ), each element is satisfied.
Φ(a
i
) shows the number of satisfied needs under a certain state of shared rule P . We
define that P N
i
is satisfied as a whole if and only if Φ(a
i
) ≥ R
l
/2, i.e., “more than half
of its elements are satisfied.”
The Proposal: The objective of each agent is to revise the shared rule to satisfy its own
needs. In this revision, one of the agents becomes the proposer and the others are voters.
The proposal is uniquely determined by the PN of the proposer. The proposer tries to
shift the shared rule toward his PN. The proposal is represented by a set of strings that
consists of “stay,” “down,” and “up” for each p
j
. The revision of a shared rule through
discussion of members should not be drastic, so the incremental/decremental value is
fixed to 1. Figure 1 shows an example. If σ = 1 and a
0
is the proposer, n
0
1
, n
0
2
are
85

p o
x
rely on
agree
disagree
antipathy
agree
disagree
(+) (-)
(+)
(+) (-)
(-)
(+) (+)
(+)
(-) (-)
(+)OR OR
imbalance balance
Fig.2. Heider’s cognitive balance and imbalance.
not satisfied by the initial P = {4, 4, 1}, so a
0
proposes {stay, down, up}. After a
1
disagrees and a
2
agrees, the number of supporters (a
0
, a
2
) exceeds that of opponents
(a
1
), so the proposal is adopted and P becomes {4, 3, 2}. Finally, Φ(a
i
) is revised to
Φ(a
0
) = 2, Φ(a
1
) = 1, and Φ(a
2
) = 3.
Social contextual Needs (SN) and Theory of Cognitive Balance. In contrast to PN,
Social contextual Needs (SN) reflect relationships with others, e.g., being close, famil-
iar, dependent. In decision-making by a small community, SN can be interpreted as that
which reflects approval/disapproval, sympathy/antipathy, and so on.
In order to analyze whether SN is balanced, we refer to the Naive Psychology pro-
posed by F. Heider [5], especially to his “Theory of Cognitive Balance.” He focused his
attention on the consistency of these relations in local setting of situations, that is, the
cognitive balance of a person (p) with another person (o) concerning an entity (x), as
shown in the left part of fig. 2.
For example, let us consider three relations:
– p agrees to a proposal x (positive (+)), and
– p relies on a person o (positive (+)), but
– o disagrees with x (negative (−)).
Accordingly, these relations are imbalanced. The balance of this triangular relation is
defined as the sign of the product of the signs of these three relations. In this case, we
have (+) × (+) × (−) = (−), so the triangular relation is imbalanced.
The balanced situation is accepted by p without stress, but the imbalanced situation
makes p stressful and uncomfortable, and is forced to be altered by emotion of p toward
restoring its balance. Concerning the above example, if p feels antipathy to o, we have
(+) × (−) × (−) = (+); if o changes his/her mind and agrees to x, we have (+) ×
(+) × (+) = (+), then p feels comfort.
Coding SN: The proposed framework interprets p, o, and x as “a voter (a
i
),” “another
voter (a
j
),” and “a proposal,” respectively. Therefore, the triangular relation consists of
three relations:
– a
i
agrees/disagrees with the proposal,
– a
i
feels a positive/negative relationship with a
j
, and
– a
j
agrees/disagrees with the proposal.
86

Each a
i
is required to make each triangle balanced by his/her emotion.
The relations between two agents (a
i
, a
j
) are assessed by the ratio of agreement by
a
i
for proposals by a
j
. Even though a
j
is now a voter, a
i
imagines the situation where
a
j
will be a proposer someday, and all possible situations are evaluated for whether a
i
wants to agree to a
j
. For this evaluation, Q-table, explained in section 2.3, is employed.
Assume the table shows that a
i
wants to agree to x cases, we define that the relation
between a
i
and a
j
is positive if and only if x ≥ 3
R
l
/2, i.e., “more than half of situations
make a
i
agree to a
j
.”
Balance of SN: We define the balance of SN of a
i
in terms of Heider’s Cognitive
Balance. SN of a
i
for each voter is represented by the above triangle, and L−2 triangles
are supposed because the number of agents is L and one of them is the proposer and
one of them is a
i
itself. We define “the satisfaction of SN of an agent a
i
as a whole” as
“more than half of triangles of a
i
are balanced.”
2.2 Framework of the Simulation
The “iterated proposal–voting simulation” is a kind of Multi-agent Simulation. In con-
trast to methods of static analysis such as power indices [7], this simulation shows
sequential shifts of states of agents, relationships among agents, and the effect of the
shared rule on agents. This simulationis partially inspired by “a game of self-amendment:
NOMIC” [11], which imitates the legislative process. All members of a community pro-
pose in turn either “establishing a new rule,” “revising a rule,” or “abolishing a rule,”
and for each proposal, members take a vote. If a proposal is approved, it becomes im-
mediately effective and shared by all members.
NOMIC is a game for humans, so rules are described in natural language. On the
other hand, our proposed simulator describes a shared rule by a set of integers and
confines the proposal to a “revision.”
Flow of “Iterated Proposal–Voting Simulation”. Our proposed “proposal-voting
simulation” shares the basic concept of NOMIC, i.e., it consists of three processes:
– an agent proposes a revision of a shared rule,
– other agents express agreement/disagreement with the proposal, and
– the revised rule affects all agents.
Furthermore, each agent learns preferences of voting by past experiences of voting and
its effect on the agent.
First, the values of fixed parameters are determined:
L: the number of agents, R
l
: the length of shared rule P ,
M: the number of iteration, R
s
: the range of the value of “each element of P .”
Then, the simulator
1. Initializes a set of agents: A = {a
0
, a
1
, a
2
, · · · , a
L−1
}.
2. Initializes a shared rule: P = {p
0
, p
1
, p
2
, · · · , p
R
l
−1
}, where each p
i
(i = 0, 1, · · · R
l
−
1) is assigned a random integer (0 ≤ p
i
< R
s
).
87

3. Repeats M times,
– for i = 0 · · · L − 1
(a) a
i
proposes a revision of P
(b) for j = 0 · · · L − 1; j 6= i
• a
j
expresses agreement/disagreement with the proposal
(c) if (agreement exceeds disagreement)
• the proposal is adopted
• P is revised
(d) for j = 0 · · · L − 1; j 6= i
• a
j
learns to revise its preference of voting
4. The final P is the result of the above decision-making.
According to the Behavioral Systems Model, each effect of the shared rule has to
affect the learning process of each a
i
.
2.3 Learning Preference of Voting
The objective of each agent is to satisfy its needs by revising the shared rule, but the
situation for each agent is not simple. It must be concerned about not only its personal
needs but also its relationships with others. We employ Q-learning [6] based on the
“ε−greedy strategy” as a learning method of agents, using the following parameters.
Range of value Q: 0.0 ∼ 1.0 zwRate of random behavior ε: 0.05
Initial value of Q: 0.5 zw Learning ratio α: 0.8
Alternatives of action: agree/disagree zw Reduction rate γ: 0.9
Each agent first perceives the current state q(a
i
, currentP ) and then selects an action
v
∗
. The selection is based on the value of Q(q, v), where v is either agree or disagree.
After voting, the state is revised to q
′
(a
i+1
, newP ), and then the value of Q(q, v
∗
)
is revised as follows:
Q(q, v
∗
) = (1 − α)Q(q, v
∗
) + α
r + γmax
Q(q
′
, v)
.
The reward r is determined by how P makes agents comfortable. Namely, it is deter-
mined by how PN and SN are satisfied. Humans tend to act to satisfy their own needs.
Our system simulates this tendency through learning voting preferences by using re-
wards that reflect satisfactions of SN and PN.
Size of Q-table The variation of the proposer is L − 1, since the number of agents is
L and one of them is a
i
itself. The value of P is estimated by a
i
according to whether
each p
j
is within a tolerance range σ. The number of p
j
is R
l
, and each p
j
is estimated
as “within σ,” “too much,” or “too small,” so the number of all possible estimations is
3
R
l
. Therefore, each Q-table has (L−1)×3
R
l
cases of states. The alternatives of action
are “agree” or “disagree.” After all, each Q-table is a matrix of {(L − 1) × 3
R
l
} × 2.
Revision of Q-value The Q-value is revised by estimation of P. After a
i
takes an action,
if P satisfies a
i
’s needs, a
i
gets positive rewards, else if P shifts far from a
i
’s needs,
a
i
gets negative rewards. Either positive or negative, a
i
gets rewards if and only if its
vote affects approval/disapproval of a proposal. In this paper, a positive reward is fixed
to 0.10, and a negative reward is fixed to −0.02.
88

3 Result of Simulation with Communication Error
Our simulation focuses on successive changes in the relationships that are important
for decision-making by a small community. These relationships are represented by SN.
This section shows the possibility of making a decision shift only by altering the rela-
tionships, without any enforcements.
3.1 Introducing Communication Error
Misunderstanding the relation with other people affects the state of SN, which reflects
the triangular relationship among an agent, a proposal, and another agent. The state
of SN affects rewards, which further affects the actions of the agent. This local per-
sonal misunderstanding yields, through iterations, global changes such as alteration of
a shared rule or the final decision.
Misperceptions of the environment, trouble in the communication route, and other
problems sometimes cause misunderstandings. We implement “misunderstandings” by
reversing the perception. Namely, if an agent a
i
misunderstands the environment, it
reversely perceives the votes of all other agents. Hereafter, the character “*” denotes
such a misunderstanding. For example, in a community A = {a
0
, a
∗
1
, a
∗
2
}, a
1
and a
2
are misperceiving the environment.
3.2 Results of Simulation
We implemented “Proposal–Voting Simulation” in C language and examined all pos-
sible combinations of normal and reversed agents. For each combination, simulations
were carried out 1,000 times, in which the order of proposals were randomly shuffled.
This section reports the mean value of 1,000 trials.
All simulations employ the following settings:
number of agents: L = 3 zwrange of the value of rules: R
s
= 7
iterations: M = 500 zwinitial value of shared rule: P = {3, 3, 3}
length of rules: R
l
= 3 zw tolerance range: σ = 1
We confirmed that shared rules are converged before 500 iterations in all simulations.
We also confirmed that the result is independent of the initial value of the common rule,
so this section only reports the case where initial P is fixed to {3, 3, 3}.
This section reports three cases, where P N
i
varies to a certain degree, P N
i
varies
drastically, and a dictatorial party exists.
Case 1: P N
i
varies to a certain degree: In the case where P N
i
varies to a certain
degree, we fix the values to N
0
= {2, 2, 1}, N
1
= {1, 1, 6}, N
2
= {4, 6, 3}.
In the normal case, i.e., there is no misperception ({a
0
, a
1
, a
2
}), P = {p
0
, p
1
, p
2
}
converges at {2.35, 2.53, 2.88}. For the other seven cases ({a
0
, a
1
, a
∗
2
} · · · {a
∗
0
, a
∗
1
, a
∗
2
}),
fig. 3 roughly illustrates the differences in final p
i
with the normal case and the final
number of satisfied PN (Φ(a
0
), Φ(a
1
), and Φ(a
2
)).
The results of shared rules are categorized clearly into two types, i.e., whether a
1
is reversed or not. When a
1
is normal, shared rules converge at almost the same value,
89

{a0, a1, a2 }
{a
0, a1, a2 }
{a
0, a1, a2 }
{a
0, a1, a2 }
* *
{a
0, a1, a2 }
*
*
{a
0, a1, a2 }
*
{a
0, a1, a2 }
**
**
{a
0, a1, a2 }
***
0.00
p1
0.00
p0
0.00
p2 Φ(a0) Φ(a1) Φ(a2)
-0.03
0.02
-0.07
0.17
0.16
0.19
0.18
-0.03
0.06
-0.06
0.04
0.05
-0.07
0.08
2.21
2.28
2.16
2.08
2.30
2.25
2.16
2.10
1.00
1.43
1.35
1.48
1.71
1.01
1.03
1.03
1.41
1.32
1.05
1.16
1.28
1.47
1.48
1.43
0.15
0.50
0.77
0.14
0.18
0.60
0.60
Fig.3. Results of case 1: (P N
i
varies).
but in any case where the perception of a
1
is reversed (denoted by a
∗
1
), the shared rule
shifts substantially. Reversing a
1
particularly affects the increase in p
2
, as shown the
meshed graphs of p
2
in fig. 3. We interpret this phenomenon based on the facts that
1. n
1
0
≃ n
2
0
∧ n
1
1
≃ n
2
1
, and
2. n
0
2
< n
2
2
< n
1
2
.
The first fact implies that p
0
and p
1
are stabilized around “2,” with which a
0
and a
1
agree, but reversing the perception of a
1
leads to a
1
agreeing with a
2
instead of a
0
.
Then the above second fact leads to p
2
shifting toward n
1
2
, and p
2
comes to the middle
value between n
1
2
and n
2
2
.
Focusing on the number of satisfied PN, neither Φ(a
0
) nor Φ(a
2
) varies, and only
Φ(a
1
) tends to be small when a
0
is reversed, as shown the meshed graphs of Φ(a
1
) in
fig. 3.
Case 2: P N
i
varies drastically: In the case where P N
i
drastically varies, i.e., for
each agent a
i
, and for each need, n
i
x
6= n
i
y
where x, y ∈ {0..R
s−1
}, x 6= y, and
n
k
j
6= n
l
j
where k , l ∈ {0..L − 1}, k 6= l. We fix these values to N
0
= {1, 3, 5}, N
1
=
{5, 1, 3}, N
2
= {3, 5, 1}. Since σ = 1, no p
i
is allowed to satisfy all of agents at the
same time.
In this case, all p
i
converge at the mean value of the allowed range. The satisfied
PN also converge at the same value, but Φ(a
i
) of the reversed agents are slightly higher
than those of other agents. These results are just what we expected. Since PN
i
varies
drastically, agents are symmetrical for any reversion.
Case 3: a dictatorial party exists: In the case where a
0
and a
1
establish a dictatorial
party, we fix values of P N
i
to N
0
= {1, 1, 1}, N
1
= {1, 1, 1}, N
2
= {4, 4, 4}.
Figure 4 roughly illustrates the differences in final p
i
for the normal case and that in
the final number of satisfied PN. In this case, both a
0
and a
1
tend to agree/disagree with
the same proposal. Therefore, the needs of a
2
are always ignored. In the normal case,
i.e., no agent is reversed, the result is just what we expected. The dictatorial party (a
0
,
a
1
) wins a great victory and it’s members needs are satisfied. The numbers of satisfied
needs, Φ(a
0
) and Φ(a
1
), mark almost the maximal value (3.00). On the other hand,
Φ(a
2
) marks almost the lowest value.
90
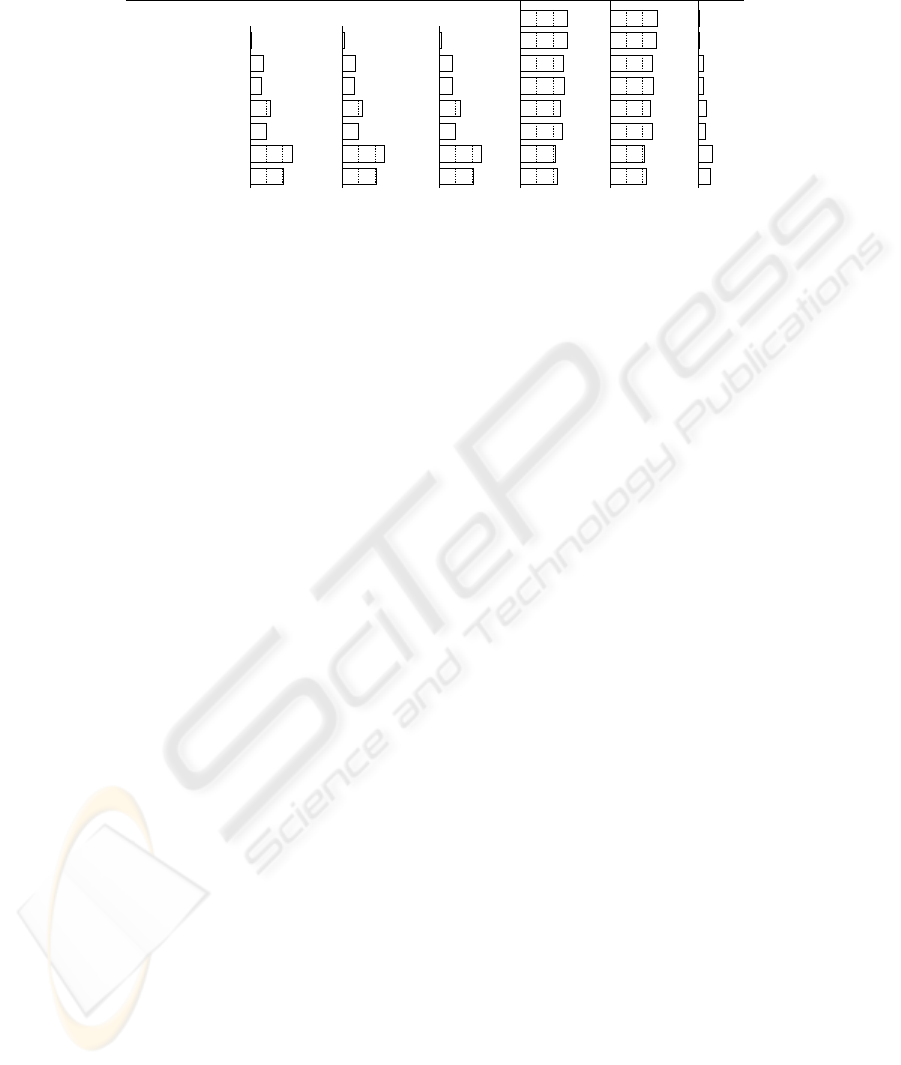
p1p0 Φ(a0) Φ(a1) Φ(a2)p2
2.90{a0, a1, a2 } 0.000.00 2.90 0.100.00
2.88{a0, a1, a2 }
*
0.01 2.88 0.120.01 0.01
2.67
{a0, a1, a2 }
*
0.08 2.67 0.33
0.08 0.08
2.70
{a0, a1, a2 }
**
0.07 2.70 0.300.07 0.07
2.52
{a0, a1, a2 }
*
0.13 2.52 0.480.13 0.13
2.61
{a0, a1, a2 }
**
0.10 2.61 0.390.10 0.10
2.12
{a0, a1, a2 }
* *
0.26 2.12 0.880.26 0.26
2.28
{a0, a1, a2 }
***
0.21 2.28 0.720.21 0.21
Fig.4. Results of the case 3: (dictatorial party exists).
In the case where the perceptions of more than one agent are reversed, the difference
between the number of satisfied needs of the dictatorial party and that of a
2
is slightly
narrower than in the normal case. In particular, when a
0
and/or a
1
have reversed per-
ceptions, the results shift far from the normal case. Even though the absolute values
are small, in the case of {a
∗
0
, a
∗
1
, a
2
}, Φ(a
2
) marks almost nine times the value of the
normal case.
4 Discussion and Conclusions
Game Theory has analyzed the effects of the scale of a community on decision-making,
the effects of personal preferences on the form of community, and so on [7][12]. Among
various approaches, power indices represent the effect (power) of party on a voting
system [7]. The Sharpley-Shubik index, Banzhaf index, and Deegan-Packle index are
known as representative ones. To compare our simulations in cases 2 and 3, power
indices are applied to a community where each of three agents forms its own party,
which consists of the agent alone. Therefore, the “voting weight” of each party is “one,”
and the approval criterion is “more than half.”
In case 2, P N
i
varies drastically, so the interests of agents are symmetrical. The
target of analysis by power indices is each voting, which correspond to a set of “a pro-
posal, voting, and the alteration of P .” Interpreting case 2 as a voting game, the major
power indices have the values shown in Table 1. On the other hand, the experimental
results show that the rate of each Φ(a
i
) against
P
j=0···L−1
Φ(a
j
) has nearly the same
value as power indices shown in Table 1. This comparison implies that, for a commu-
nity in which P N
i
varies as case 2, the satisfaction of each agents can be predicted by
using the power indices.
In case 3, the three indices have the values shown in Table 1. In each index, the dicta-
torial party {a
0
, a
1
} wins perfectly. As shown in Table 1, the rate of each Φ(a
i
) against
P
j=0···L−1
Φ(a
j
) is almost the same as the indices when no communication error is
allowed, i.e., the case of {a
0
, a
1
, a
2
}. On the other hand, these rates drift, especially
in the case of {a
∗
0
, a
∗
1
, a
2
} where both members of the dictatorial party contains mis-
perception. This comparison implies that when a dictatorial party exists static analysis,
91

Table 1. Power Indices and Φ (a
i
) in case 2 and 3.
case 2 case 3
index
a
0
a
1
a
2
{a
0
, a
1
} {a
2
}
Sharpley-Shubik 1/3 1/3 1/3 2/2 0/2
Banzhaf 4/12 4/12 4/12 4/4 0/4
Deegan-Packle 1/3 1/3 1/3 1/1 0/1
Rate of Φ(a
i
) at {a
0
, a
1
, a
2
} 178/532 175/532 179/532 290/300 10/300
Rate of Φ(a
i
) at {a
∗
0
, a
∗
1
, a
2
} 212/300 88/300
such as the use of power indices, is not always applicable. In some cases, the behavior
following the iterated voting process shows some special phenomena.
Remarkable progress has been made in communication technology to overcome the
diverse cases where trivial communication error causes unexpected serious results. This
paper reported that some kind of misperception influence the final result of a “proposal–
voting system” and that the type of misperception makes a difference in the results. In
particular, we investigated three cases: where personal needs vary to a certain degree,
where they vary drastically, and where there exists a dictatorial party.
By following the process of iterated proposals and voting, the proposed framework
of decision-making can show phenomena that cannot be detected by static analysis
methods. We are now planning to extend our simulation to a method for analyzing
phenomena related to decision-making by humans, such as risky shifts, cautious shifts,
and so on.
References
1. Yamaguchi, H.: Social Psychology of Majority Formation Behaviors. Nakanishiya Shuppan
(in Japanese). (1998)
2. Stoner, J.A.F.: A comparison of individual and group decisions involving risk. Master’s the-
sis. Massachusetts Institute of Technology, School of Industrial Management. (1961)
3. http://www.dis.titech.ac.jp/coe/
4. George, J.B.: Nursing Theories, The Base for Professional Nursing Practice. Appleton &
Lange, A Simon & Schuster Company. (1995)
5. Heider, F.: The Psychology of Interpersonal Relations. John Wiley (1961)
6. Sutton, R.S., Barto, A.G.: Reinforcement Learning. The MIT Press (1998)
7. Muto, S., Ono, R.: Game Theoretical Analysis of Voting Systems. Nikkagiren (in Japanese).
(1998)
8. Ueda, H., Tanizawa, T., Takahashi K., Miyahara T.: Acquisition of Reciprocal Altruism in a
Multi-agent System. Proc. of IEEE TENCON2004, (2004). B334.pdf
9. Wesley, R.L.: Director of Nursing. Rehabilitation Institute of Michigan (1998)
10. Nightingale, F.: Notes on Nursing - What it is and what it is not -. Bookseller to the Queen,
London (1860)
11. Nomic A Game of Self-Amendment.
http://www.earlham.edu/ peters/nomic.htm
12. Axelrod, R.: The Complexity of Cooperation: Agent-Based Models of Competition and Col-
laboration. Princeton University Press (1997)
92
