
Blind Source Separation Based on a Single Observation
Damjan Zazula, Aleš Holobar
University of Maribor, Faculty of EE and CS
Smetanova 17, 2000 Maribor, Slovenia
Abstract. This paper deals with a novel approach to the compound signal
decomposition. It takes adv
antage of blind source separation using the
algorithm for convolution kernel compensation (CKC). We derive a version
which cope with compound signals, mixtures of several source contributions,
even if only a single observation is available. Our novel approach detects and
separates the triggering instants of all source symbols which contribute to the
processed observation. The obtained decomposition is very robust and accurate.
We experimented with synthetic signals having characteristics similar to the
electrocardiographic (ECG) signals. Also at signal-to-noise ratios (SNRs) as
low as 0 dB, the obtained average true positive statistics for the detected source-
symbol triggerings was 98±1%, average false positive statistics 2±1%, and false
negative statistics 3±2%.
1 Introduction
Many natural and technological phenomena can be modelled as multiple-input
multiple-output (MIMO) systems. Observing compound signals, for example, such as
telecommunication, bioelectrical, seismic, speech or imaging data, successful
approaches are sought to perform a thorough decomposition to the signals’ constituent
components. These components observed, i.e. measured, at multiple system outputs
carry simultaneous information on each system input excitation, which is said to come
from a source, and on the response of the transmission path between a source and an
observation point, i.e., a system channel [1, 2].
On the other hand, any compound signal can be interpreted as a superimposition of
si
gnal components, which correspond to the individual source symbols generated by
the MIMO input sources. These components, therefore, appear at time instants which
coincide with the triggering (generating) instants of the sources. If the symbol
alphabet is finite, so is the number of different observed signal components. By
reformulating the model in such a way that it describes the observed signal
components and their triggering instants, the characteristics of source symbols and the
model transfer channels are not seen separately any more [1]. There are several
benefits out of this assumption. The first of them brings unification to the
interpretation of all compound signals, regardless their original sources. Secondly,
decomposition of those signals can be focused on the component triggering instants,
which greatly improves its accuracy, robustness, and reliability. So, the
Zazula D. and Holobar A. (2006).
Blind Source Separation Based on a Single Observation.
In Proceedings of the 2nd International Workshop on Biosignal Processing and Classification, pages 76-85
DOI: 10.5220/0001224100760085
Copyright
c
SciTePress

decomposition result is a train of triggering pulses. And finally, the observed
individual signal components may be extracted from the observations by different
approaches, such as spike-triggering averaging [11].
Typical observations of compound signals in practice are related to
communications, bioelectrical signals, range imaging, etc. If the input source symbols
can be considered spatially and temporally uncorrelated, a variety of blind source
separation (BSS) techniques serve the decomposition purpose accordingly [3, 4, 5, 6,
7, 8]. When the sources tend to become correlated, more reliable solutions may be
expected using higher-order statistics (HOS) [9, 10], which are also very noise-
resistant. While the BSS methods cope with nonstationary signals, HOS approaches
cannot. On the other hand, the number of observations must exceed the number of
sources to warranty a reliable BSS operation, whereas for HOS there is no such
limitation [10, 11].
Recently, a novel BSS-based method has been proposed. It makes use of the
Mahalanobius distance and angle calculation which, consequently, can lead to the
entire model convolution kernel compensation (CKC). As a result, the system output
observations are blindly deprived of the transfer channel influence and only the
source-symbol triggering pulse trains are extracted [11, 12]. It has been shown that
the source symbols correlated up to 10 % and the underdetermined cases with the
number of observations being as low as a half of the number of source symbols do not
hinder a proper CKC-based decomposition [12].
This paper proposes a novel solution which combines the benefits of the CKC and
HOS approaches. It can cope with an arbitrary underdetermined case in such a way
that it generates additional observations out of the given ones. This generation must
be based on nonlinear operations on the given observations–the linear ones wouldn’t
increase the rank of the CKC decomposition matrix. To demonstrate the idea in an
extreme situation, we are going to deal with only a single observation here, so the
anticipated model will be reduced to a multiple-input single-output (MISO). Adequate
data model and the CKC-based decomposition are presented in Section 2. Section 3
introduces the idea of how to generate more observations out of a single one, while
Section 4 explains this new concept with a short example. The influence of noise and
correlated sources is discussed in the concluding Section 5.
2 Data Model
Recapitulate briefly the reconstruction of source-symbol pulse trains using the CKC-
based decomposition [11, 12]. Consider the following data model:
∑∑
=
−
=
=+−=
K
j
L
k
ijiji
Minvkntkcnx
1
1
0
,,1);()()()( …
(1)
where x
i
(n) stands for the i-th observation, c
ij
(k) corresponds to the contribution of
length L of the j-th source symbol in the i-th observation, and t
j
(n-k) denotes a
sequence of triggering instants for this symbol, , with unit-
sample pulses placed at T
∑
∞
−∞=
−=
l
jj
lTnnt ))(()(
δ
j
(l) lags, while v
i
(n) is considered i.i.d. white noise
independent from the sources.
77

It has been shown [3] that Eq. (1) can be transformed into a multiplicative vector
form as follows:
1,,0);()()(
−
=+= Nnnnn
eeee
…vtCx
(2)
where subscript e designates extended vectors and matrices, C
e
contains the observed
contributions of source symbols:
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
MKM
K
e
CC
CC
C
1
111
(3)
with
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
=
)1()0(0
0)1()0(
Lcc
Lcc
ijij
ijij
ij
C
, (4)
x
e
(n) stands for the vector of observations, and t
e
(n) for the vector of triggering
pulses, both at lag n:
T
eKKee
T
eMMee
MLntntMLntntn
MnynyMnynyn
)]2(),....,(),....,2(),....,([)(
)]1(),....,(),....,1(),....,([)(
11
11
+−−+−−=
+−+−=
t
x
(5)
Extended noise vector v
e
(n) is considered constructed in the same way. M
e
in Eqs.
(5) means an extension factor. If it fulfils the following inequality
)1( −+≥⋅
ee
MLKMM
, (6)
then for K different source symbols of length L and M observations the matrix C
e
is of
full column rank. This condition warranties a successful elimination of contributions
of C
e
, as we are going to show in the next section.
2.1 Convolution Kernel Compensation
Recall Eq. (2). It has a typical MIMO structure. From this point of view, Ce is a
convolution kernel convolving t
e
(n) into the observations x
e
(n). Given x
e
, if we can
get rid of C
e
the triggering instants of unknown source symbols, t
e
, would be
obtained. We called this process “convolution kernel compensation (CKC)”.
Observe the following expression:
)()(
1
nn
e
T
e
e
xRx
x
−
(7)
where stands for the sample correlation matrix:
e
x
R
ICRCICttCxxR
tx
22
σσ
+=+==
T
ee
T
e
T
eee
T
ee
ee
(8)
with denoting sample correlation matrix of source triggering trains of pulses,
and the expression σ
e
t
R
2
I represents the noise, v
e
, correlation matrix.
For easier comprehension of derivation, continue with the noise-free case. By
substituting (8) into (7), we see that convolution kernel is eliminated:
)()()()()()(
1111
nnnnnn
e
T
eeee
T
e
T
e
T
ee
T
e
eee
tRttCCRCCtxRx
ttx
−−−−−
==
(9)
78

The expression from (7) is known as Mahalanobius distance, which, as it is clear
from Eq. (9), yields only the information on source triggering instants. Actually, its
value depends on the number of sources active in given time instant n. This is why we
call it activity index.
Suppose we deal with orthogonal sources and n
0
indicates the time instant where
one of them generates a symbol (its contribution appears in the observation). Then
vector t
e
(n
0
) is all zero except the element which belongs to the generated symbol, say
the i-th, and equals 1. Besides, matrix is diagonal, and so is . It is then
straightforward that
e
t
R
1−
e
t
R
)()()()()()()()(
,,,0,,
1
0
1
0,
0
ntrntntrnnnnnp
ieiiieieiie
T
ee
T
ein
ee
====
−−
tRtxRx
tx
(10)
where r
i,I
denotes the i-th diagonal element of , and t
1−
e
t
R
e,i
(n) stands for the train
value at lag n for the i-th source symbol. Evidently, taking all possible n’s into
account, Eq. (10) produces a sequence
in ,
0
p
whose values equal the i-th source-
symbol triggering pulse train to a constant amplitude factor, r
i,i
. So, all repetitions of
that symbol are detected.
The values of activity index indicate those lags n
i
where individual sources
contribute their symbols. If we select such n
i
’s that cover all different source contribu-
tions, a thorough decomposition is done and all source-symbol triggering pulse trains,
t
i
; i∈[1,K], are separated.
Once the triggering instants of the signal components, i.e. the source-symbol pulse
trains, are known, also the components themselves can be obtained–for example, by
using the spike-triggered averaging throughout the given observations.
3 An Upgrade of the CKC-based Decomposition Using a Single
Observation
Suppose the data model from Eq. (1) represents a MISO instead of a MIMO system–
so, only a single observation x
1
(n); n=0,…,N-1, is available. The necessary condition
(6) for a thorough decomposition can, therefore, not be met.
Now, try to increase the number of observations artificially as follows. Assuming
every observed sample x
1
(n) an independent random variable, new observations may
be generated using higher-order moments of these variables. Also cross-moments may
be applied by combining the variables at different observation lags. In the
continuation, we will talk only the moments at a given lag, actually meaning the dot-
operations (according to MATLAB) with the given shift of the observation
repetitions. This will give additional, artificial observations; however, it will also
produce additional, artificial source symbols. For instance, taking the second-order,
zero-lag moments, all the observation samples that comprise superimpositions of
several source activities will generate new artificial sources whose activity is
determined by pair-wise logical products of the superimposed source activities. Such
artificially introduced source symbols will be called cross-symbols, s
ij
(n), if i and j are
79

two intersecting, superimposed sources in the observation sample n, s
ij
(n)=s
i
(n)·s
j
(n-
d
ij
), where d
ij
is a time shift between the triggerings of sources i and j.
Any zero-lag higher-order moment can generate one additional (artificial)
observation. How about the nonzero lags? Suppose source triggers with a minimum
distance of T
min
between the adjacent symbols. Suppose also those source symbols
contribute signal components whose length in observation equals L, L<T
min
. It is
necessary, then, to limit the lags respected in higher-order moments to Λ=T
min
-L. This
assumption is correct with all possible applications mentioned in Section 1.
Remember we have only a single observation available, x
1
. Hence, all additional,
artificial observations will be derived from it. Denote them by y and a set of indexes:
the number of indexes is going to be equal to the order of moments applied, and the
values of indexes are going to define the shifts among the combined observation
repetitions. Make this more comprehensible by a short example; let
[]
65432101
,,,,,,)( aaaaaaanx =
be an observation which can be further designated as
{}
)()(
10
nxny
=
.
Second-order moments at zero lag will be calculated as:
{}
[
]
2
6
2
5
2
4
2
3
2
2
2
1
2
00,0
,,,,,,)( aaaaaaany =
giving the first artificial observation whose sample values equal the squares of the
values in x
1
. Further non-zero lags are possible, such as:
{}
[
]
0,,,,,,)(
6554433221101,0
aaaaaaaaaaaany =
with the second repetition of x
1
shifted anticausally by one sample. Also y
{0,-1}
(n) is
feasible, but because y
{0,-1}
(n)= y
{0,1}
(n) no new observation is obtained.
We have already mentioned that added artificial observations introduce new source
symbols as well. Actually, they contribute new signal components which consist of
non-linear combinations of the responses to the original source symbols. Whenever a
superimposition of two or more source contributions appear in an observation sample,
the artificial observations based on higher-order moments need also additional,
artificial sources to be modelled by MIMO. Exemplify this statement by a concrete
situation. Suppose we have two components, c
ij
(n)=[a
1
,a
2
,a
3
] and c
ik
(n)=[b
1
,b
2
,b
3
],
superimposed in our observation, so that:
x
1
(n)=[a
1
,a
2
,a
3
,0,a
1
,a
2
+b
1
,a
3
+b
2
,b
3
,0,b
1
,b
2
,b
3
]
It is obvious that c
ij
(n) appears alone first, then at location 4 it overlaps with c
ik
(n-
1), while at location 9 c
ik
(n) appears alone. Using the triggering train of pulses, t, a
matrix form follows:
[]
tC ⋅=
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
1,0,0,0,1,0,0,0,0,0,0,0
0,1,0,0,0,1,0,0,0,0,0,0
0,0,1,0,0,0,1,0,0,0,0,0
0,0,0,0,0,1,0,0
,0,1,0,0
0,0,0,0,0,0,1,0,0,0,1,0
0,0,0,0,0,0,0,1,0,0,0,1
,,,,,)(
3213211
bbbaaanx
Let us now construct the artificial observation with second-order moments at zero
lag:
{}
],,,0,,2,2,,0,,,[)(
2
3
2
2
2
1
2
3
2
223
2
3
2
112
2
2
2
1
2
3
2
2
2
10,0
bbbbbbaabbaaaaaany ++++=
80

The original observation and the added artificial one can be described by a unified
matrix form:
{}
tC ⋅=
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
0,0,0,0,0,1,0,0,0,0,0,0
0,0,0,0,0,0,1,0,0,0,0,0
1,0,0,0,1,0,0,0,0,
0,0,0
0,1,0,0,0,1,0,0,0,0,0,0
0,0,1,0,0,0,1,0,0,0,0,0
0,0,0,0,0,1,0,0,0,1,0,0
0,0,0,0,0,0,1,0,0,0,1,0
0,0,0,0,0,0,0,1,0,0,0,1
2,2,,,,,,
0,0,,,,,,
)(
)(
2312
2
3
2
2
2
1
2
3
2
2
2
1
321321
0,0
1
bababbbaaa
bbbaaa
ny
nx
(11)
Both the convolution kernel C and the triggering pulse trains change by adding
artificial observations. From Eq. (11), it is clear how new sources are artificially
introduced and what is their role (see the two bottom rows in t).
Eq. (11) also explains the most important contribution of added artificial
observations: the rank of convolution kernel C increases. When dealing with finite
alphabet of source symbols, e.g. K, it can be shown that with adequate number of
artificial observations the convolution kernel matrix C obtains full column rank. This
leads to a signal decomposition which is Bayesian optimal, as defined in the
preceding section [13].
The only problem of this kind of approach is that the decomposed source-symbol
triggering trains split among several artificial sources. Whenever there are
superimpositions of source-symbol contributions within an observation, every type of
superimposition is decomposed to its own triggering pulse train. Consequently, the
triggerings which appear in those trains disappear from the trains of the sources
whose symbol contributions overlap.
There are practical cases where this effect is not disturbing. This certainly is true for
the observations with non-overlapping contributions, such as electrocardiograms
(ECG) or, partially, images. We are going to elaborate our approach with non-
overlapping assumption in the next section.
4 Simulation Results
To exemplify the derivation from Section 3, we decided to simulate an artificial
observation with characteristics similar to the ECG signals. We synthesised the
following:
1.
four random generated source contributions with lengths L = 8, 10, 5 and 7
samples, respectively;
2. random appearance of these source contributions in the generated observation,
so that their intermediate mean distances were 50, 1000, 500, and 3000
samples, respectively, while actual appearances were Gaussian distributed
around these values with standard deviation of 2 samples;
81
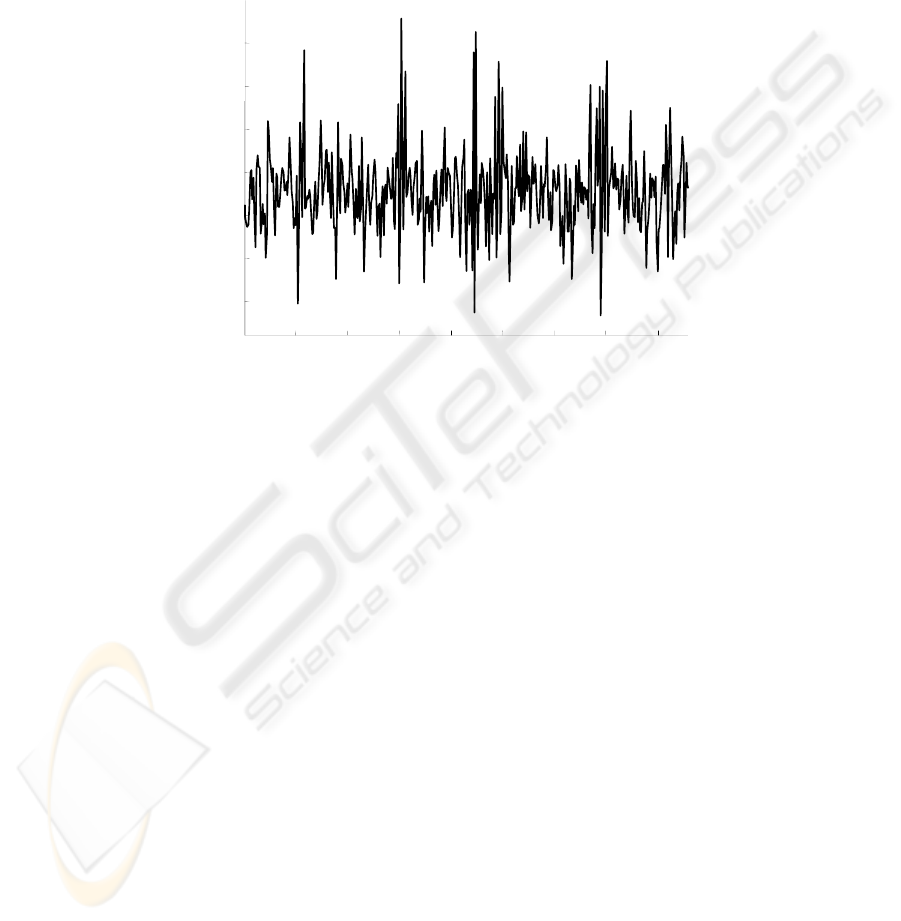
3. the generated observation with length of 10000 samples;
4. artificial observations up to the power of p=3 and shift Λ=4 (according to the
assumptions in Section 3).
Thus, the simulated observation contains four different source contributions. The
one belonging to the first source is most frequent and could be understood as normal
systoles. The other three could be interpreted as different abnormal heart beats, i.e.
extrasystoles and possible pathological changes.
1550 1600 1650 1700 1750 1800 1850 1900
-0.5
-0.4
-0.3
-0.2
-0.1
0.0
0.1
Samples
Amplitude [arbitrary units]
1550 1600 1650 1700 1750 1800 1850 1900
-0.5
-0.4
-0.3
-0.2
-0.1
0.0
0.1
Samples
Amplitude [arbitrary units]
Fig. 1. The generated synthetic observation contaminated with 0 dB additive zero-mean
Gaussian noise. Only a part of the generated signals is depicted.
The total number of artificial observations was 20. We set the number of extended
observations to M
e
=2 (Eq. (6)). Using our CKC approach [11, 12], we verified the
accuracy of the decomposed triggering pulse trains for the four simulated sources.
Simulations were performed in 10 Monte Carlo runs with different levels of additive
Gaussian noise, so that the SNRs were 20, 15, 10, 5, and 0 dB. An example of the
processed observation with 0 dB additive Gaussian noise is depicted in Fig. 1. Fig. 2
illustrates the decomposition results in the form of the detected triggering pulse trains
for the first source. Trains in black were decomposed at different SNRs, as indicated.
The bottom train of Fig. 2 (in grey) is the original triggering pulse train for the first
source.
82

200 400 600 800 1000 1200 1400
20
15
10
5
0
Samples
SNR [dB]
200 400 600 800 1000 1200 1400
20
15
10
5
0
Samples
SNR [dB]
Fig. 2. Reconstructed triggering pulse sequences of source 1 at different SNRs (black) and
original simulated pulses (grey at the bottom). Only a part of the reconstructed pulse sequences
is depicted.
A more detailed analysis of the obtained results versus different SNRs is given in
Tables 1, 2, and 3. Table 1 describes percentages of correctly detected triggering
instants for all four sources (true positive statistics). A triggering instant was
considered correctly detected when the decomposition returned the exact position of
an original source triggering. Tables 2 and 3 collect percentages of false positive and
false negative statistics, respectively.
Table 1. Percentage (mean ± standard deviation) of accurately recognized triggering pulses
(true positive statistics) versus SNR.
SNR 20 dB 15 dB 10 dB 5 dB 0 dB
Source 1
1.00±0.00 0.98±0.02 0.98±0.02 0.99±0.01 0.98±0.01
Source 2
1.00 ± 0.00 0.96 ± 0.01 1.00 ± 0.00 1.00 ± 0.00 0.97 ± 0.01
Source 3
0.99 ± 0.02 1.00± 0.00 0.99 ± 0.02 0.99 ± 0.02 1.00 ± 0.00
Source 4
1.00 ± 0.00 1.00 ± 0.00 1.00 ± 0.00 1.00 ± 0.00 1.00 ± 0.00
Table 2. Percentage (mean ± std) of misplaced pulses (false positive statistics) versus SNR.
SNR 20 dB 15 dB 10 dB 5 dB 0 dB
Source 1
0.00± 0.00 0.02 ± 0.02 0.02 ± 0.02 0.01± 0.01 0.02 ± 0.01
Source 2
0.00± 0.00 0.04 ± 0.01 0.00 ± 0.00 0.00 ± 0.00 0.03 ± 0.01
Source 3
0.01± 0.02 0.00± 0.00 0.01 ± 0.02 0.01 ± 0.02 0.00 ± 0.00
Source 4
0.00± 0.00 0.00 ± 0.00 0.00 ± 0.00 0.00 ± 0.00 0.00 ± 0.00
Table 3. Percentage (mean ± std) of missed pulses (false negative statistics) versus SNR.
SNR 20 dB 15 dB 10 dB 5 dB 0 dB
Source 1
0.01± 0.01 0.04 ± 0.01 0.04 ± 0.02 0.03 ± 0.01 0.04 ± 0.02
Source 2
0.01 ± 0.01 0.04 ± 0.03 0.03 ± 0.03 0.03 ± 0.02 0.03 ± 0.01
Source 3
0.01 ± 0.02 0.01 ± 0.02 0.02 ± 0.03 0.03 ± 0.04 0.02 ± 0.03
Source 4
0.00 ± 0.00 0.00 ± 0.00 0.00 ± 0.00 0.00 ± 0.00 0.00 ± 0.00
83

It is obvious that our method is very robust. The worst percentage of the recognised
source triggering instants for the first source is 98%, for the second source 96%, for
the third source 99%, and for the fourth source 100%. As we can see from the tables,
even an extremely high noise with SNR=0 dB does not decrease the successful rate of
the recognised triggering pulses, regardless the triggering frequency as well.
5 Discussion and Conclusions
We have derived an approach which makes a MIMO system decomposition possible
based only on a single observation. It is applicable in the cases with orthogonal, or at
least close-to-orthogonal, sources whose inter-triggering distance is lower bounded.
As already mentioned, an obvious application is ECG signals. The systoles cannot
overlap, and there is always an inter-systole gab which warranties that also the
extended observations would not cause severe overlappings. Referring to the original
MIMO decomposition from [11, 12], two important differences must be reported
here:
1. Nonlinear procedures for generation of artificial observations influence additive
noise which is presumed zero-mean and, thus, prone to elimination by averaging of
the signal samples. Consequently, the observations obtained with the even powers
contain additive noise which is not zero-mean any more. This effect decreases the
algorithm’s robustness.
2. In the MIMO decomposition from [11, 12], it is enough to locate a firing of a
single source, say n
0
, and x
e
(n
0
) can readily be used to extract the complete pulse train
for the source symbol in question (Eq. (10)). The statement equally holds for all
sources in the newly proposed approach described in this paper, so for the cross-
symbols as well. This means that the firing positions of a source symbol will not be
detected when using x
e
(n
0
), if n
0
is a time instant where this source symbol overlaps
with any of other symbols. To detect a single source symbol’s triggering instants, it is
important to find such n
0
where this symbol appears alone. On the contrary, each point
of a multiple source activity would be recognised as a firing of that artificial source
which was generated by the overlapped multiple source symbols.
To cope with the two problems, special noise-reduction techniques must be
implemented and additional post-processing stages are needed to fuse the detected
pulse trains which belong to the same original source symbol. Both needs further
investigation and explanation which goes beyond the scope of this paper.
Our simulation confirmed that even from a single observation and in very noisy
environment a reliable separation of several sources is feasible using the CKC
approach. Source-symbol triggering instants can be recognised in more then 98% of
cases even when SNR goes as low as 0 dB. This is a very important conclusion for
some practical implementations. Analysing ECG signals, for example, a low number
of observations, if not only a single observation, is available. Nevertheless, the
proposed approach improves significantly the chances of different types of abnormal
heart beats to be recognised and separated from the normal systoles, while for all the
beats their fiducial points can be determined with high precision.
84

Acknowledgements
This work was partially supported by the NEW project within the European 5
th
Framework Programme, and partially by the Slovenian Research Programme Funding
Scheme P2-0041.
References
1. Zazula, D., Korže, D., Šoštarič, A., Korošec, D.: Study of Methods for Decomposition of
Superimposed Signals with Application to Electromyograms. In: Pedotti et al. (eds.):
Neuroprosthetics, Springer Verlag, Berlin (1996).
2. Prakriya, S.: Eigenanalysis-based blind methods for identification, equalization, and
inversion of linear time-invariant channels. IEEE Transactions on Signal Processing, Vol.
50, 7 (2002) 1525-1532.
3. Cardoso, J. F.: Blind signal separation: statistical principles. Proceeding of the IEEE.
Special issue on blind identification and estimation, Vol. 9, 10 (1998) 2009-2025.
4. Tong, L., Liu, R.: Blind estimation of correlated source signals. In: Proc. Asilomar Conf.
(1990) 161-164.
5. Belouchrani, A., Meraim, K. A., Cardoso, J. F., Moulines, E.: A blind source separation
technique based on second order statistics. IEEE Transactions on signal processing, Vol.
45, 2 (1997) 434-44.
6. Pham, D. T., Cardoso, J. F.: Blind separation of instantaneous mixtures of non stationary
sources. IEEE Transactions on Signal Processing, Vol. 49, 9 (2001) 1837-1848.
7. Belouchrani, A., Moeness, A. G.: Blind source separation based on time-frequency signal
representation. IEEE Transactions on Signal Processing, Vol. 46, 11 (1998).
8. Holobar, A., Fevotte, C., Doncarli, C., Zazula, D.: Single autoterms selection for blind
source separation in time-frequency plane. In: XI European Signal Processing Conference
EUSIPCO 2002, Toulouse, France (2002) 4 pp.
9. Nikias, C. L., Petropolu, A. P.: Higher-Order Spectra Analysis: A Nonlinear Signal
Processing Framework. Prentice Hall signal processing series, Englewood Cliffs (1993).
10. Zazula, D., Karlsson, S., Doncarli, C.: Advanced signal processing techniques. In R.
Merletti, P. Parker (eds.), Electromyography: physiology, engineering, and noninvasive
applications. John Wiley & Sons, Hoboken, NJ (2004) 259-304.
11. Holobar, A., Zazula, D.: Correlation-based decomposition of surface electromyograms at
low contraction forces. Med. biol. eng. comput., Vol. 42, 4 (2004) 487-495.
12. Holobar, A., Zazula, D.: Correlation-based approach to multichannel blind deconvolution
of binary sources. Submitted to IEEE Trans. on Sig. Proc.
13. Kay, S. M.: Fundamentals of Statistical Signal Processing. Prentice-Hall International,
London (1993).
85
