
COOPERATIVE MAP BUILDING USING QUALITATIVE
REASONING FOR SEVERAL AIBO ROBOTS
David Graullera, Salvador Moreno
Instituto de Robótica,Universidad de Valencia, Paterna, Valencia, Spain.
M. Teresa Escrig
Departamento de Ingeniería y Ciencia de los Computadores, Universitat Jaume I, Castellón, Spain.
Keywords: Qualitative Reasoning, Cooperative Map Building, Multi-Robot System.
Abstract: The problem that a robot navigates autonomously through its environment, builds its own map and localizes
itself in the map, is still an open problem. It is known as the SLAM (Simultaneous Localization and Map
Building) problem. This problem is made even more difficult when we have several robots cooperating to
build a common map of an unknown environment, due to the problem of map integration of several
submaps built independently by each robot, and with a high degree of error, making the map matching
specially difficult. Most of the approaches to solve map building problems are quantitative, resulting in a
great computational cost and a low level of abstraction. In order to fulfil these drawbacks qualitative models
have been recently used. However, qualitative models are non deterministic. Therefore, the solution recently
adopted has been to mix both qualitative and quantitative models to represent the environment and build
maps. However, no reasoning process has been used to deal with the information stored in maps up to now,
therefore maps are only static storage of landmarks. In this paper we propose a novel method for
cooperative map building based on hybrid (qualitative+quantitative) representation which includes also a
reasoning process. Distinctive landmarks acquisition for map representation is provided by the cognitive
vision and infrared modules which compute differences from the expected data according to the current map
and the actual information perceived. We will store in the map the relative orientation information of the
landmarks which appear in the environment, after a qualitative reasoning process, therefore the map will be
independent of the point of view of the robot. Map integration will then be achieved by localizing each
robot in the maps made by the other robots, through a process of pattern matching of the hybrid maps
elaborated by each robot, resulting in an integrated map which all robots share, and which is the main
objective of this work. This map building method is currently being tested on a team of Sony AIBO four
legged robots.
1 INTRODUCTION
An autonomous mobile robot, able to explore an
unknown but structured environment, must first be
able to perform several related tasks, which can be
illustrated by the answers to the following questions
(Levitt, 1990):
• What should I remember? (mapping)
• Where am I? (localization)
• Where should I go? (path planning)
• How can I go? (motion control or navigation)
Acquiring and maintaining internal maps of the
world is a necessary task to carry out a successful
navigation in complex environments.
We are going to solve in this paper the problem
of map building for several cooperating autonomous
mobile robots on an unknown labyrinth made of
rectangular walls. The walls are distributed
randomly forming a labyrinth and the robots are left
inside with no knowledge of the environment. The
robots have to explore the environment and to
cooperate to build a map of the environment.
There are in the literature a lot of approaches for
building maps in static, structured and relatively
229
Graullera D., Moreno S. and Escrig M. (2006).
COOPERATIVE MAP BUILDING USING QUALITATIVE REASONING FOR SEVERAL AIBO ROBOTS.
In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 229-234
DOI: 10.5220/0001218502290234
Copyright
c
SciTePress

small environments. They can be divided into three
main strategies: qualitative, quantitative and hybrid
approaches.
Qualitative models focus on the boundaries of
the objects, making divisions of the space more or
less detailed. These approaches deal with imprecise
information in a manner inspired by the cognitive
processes used by humans. The qualitative concept
of a topological map, which represents the world
using nodes (places) and arcs (relations), has been
used in several approaches, such as the one
introduced by (Kuipers, 1978). Another model is
defined by (Freksa, 2000), where schematic maps
are used to reason about relative positions and
orientations. Other qualitative models have been
carried out by several authors. Most of these
qualitative models have been implemented mainly in
simulations.
Quantitative methods represent the environment
by metrical information obtained by the sensors. The
major exponent of this strategy is the grid-based
model, introduced by (Moravec and Elfes, 1985).
Quantitative models are affected by odometric and
sensory errors. In recent years, many quantitative
approaches have been developed using probabilistic
techniques to cope with partial and inaccurate
information. All of these approaches are based in
implementations of the Bayes filter, as the Kalman
filter, hidden Markov models, partially observable
Markov decision processes or Monte Carlo
localization. A survey on this techniques can be
found in (Thrun, 2001) and (Thrun, 2002).
Hybrid approaches handle with qualitative and
quantitative information, combining the best of the
each model. One of the first models for map
building was proposed by (Thrun, 1998), which
combines the occupancy grids with topological
maps. Other hybrid models can be found in
numerous papers, as (Escrig, 2005). More hybrid
models use probabilistic techniques to cope with
partial information.
The work presented in this paper represents
hybrid information into a map: quantitative data
provided by robot sensors (most of the times this
data contain imprecision); and qualitative data.
Moreover, our approach is going to use a qualitative
reasoning process which will allow us to solve the
four problems above mentioned: mapping,
localization, planning and navigation.
2 COOPERATIVE MAP
BUILDING
We are going to solve the problem of cooperative
map building for several autonomous mobile robots
on an unknown labyrinth made of rectangular walls.
We suppose each robot is able to explore an area in
front of it, in order to detect if this area is free or if it
is occupied by one or more walls, or by other robot.
Taking into account that the walls are straight, each
robot must detect the distance and orientation of
each wall which enters in its exploring area, and the
position of a circle enclosing each other robot it
detects in the area. In the case of AIBO robots, we
have implemented a multisensory approach to
explore this area, by using the TV camera of the
robot, and the infrared range sensor.
The cooperative map building procedure is
composed of the following steps:
• Individual Map Building
• Map Sharing and Self-Localization
• Integrated Map Building
3 INDIVIDUAL MAP BUILDING
For each robot, we build a individual map taking as
input the distance and orientation of each wall which
enters in its exploring area, and the position of a
circle enclosing each other robot it detects in the
area, and have as output the generated map, and the
orders to the robot for exploring the environment, in
the terms of “walk XX centimetres”, and “turn YY
degrees”.
3.1 Initialization
At the beginning, the robot map is empty, and the
robot detects nothing in the area in front of it,
therefore it assumes the initial hypothesis that the
scenario is composed of an infinite floor surface,
without walls, with only an explored point: the
current position of the robot. The robot starts
walking ahead until the explored area in front of the
robot is occupied by a wall. This situation can be
seen at the snapshot 1 of figure 1. Each step the
robot gives is memorized in the database (only to
make an approximate evaluation of the distance the
robot walks in free walking). When the robot detects
a wall, it enters into the wall following mode.
ICINCO 2006 - ROBOTICS AND AUTOMATION
230
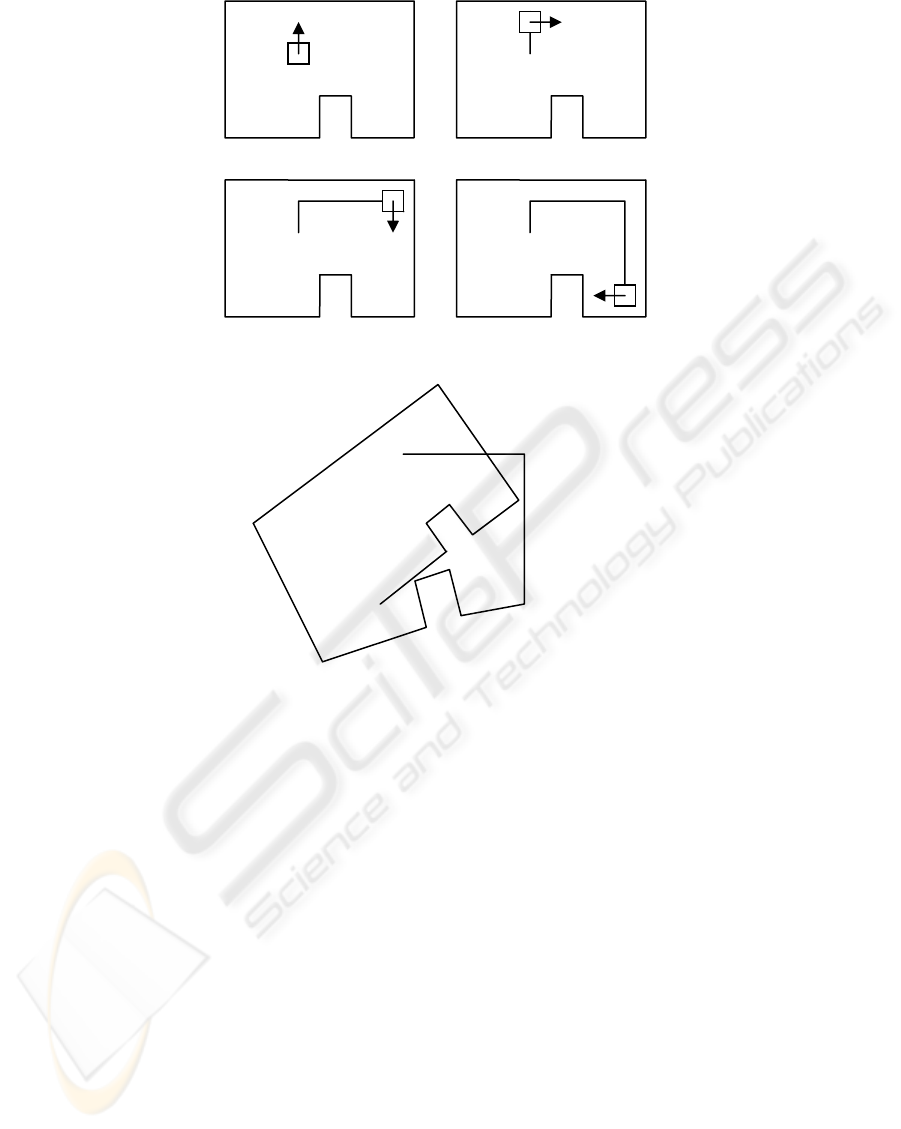
3.2 Wall Following
When the robot detects an unknown wall, it starts
following the wall by turning right and following the
wall. While it is walking along a straight wall, it
stores the distance it walks as an approximate
measure of the length of the wall. When it reaches a
corner, it labels the corner and it stores the
approximate turning angle of the corner before start
following a new wall. This process can be seen at
snapshots 2, 3 and 4 of figure 1.
Nevertheless, the process is not as simple as
this. The imprecise information about robot position
and orientation given by odometry, makes
impossible to generate a map of the scenario as the
one shown in figure 1. In fact, the real map is more
or less as the one shown in figure 2.
The map information stored in the database
when the robot discovers point d is the following:
point(nonreal,p01).
point(real,a,95).
line(p01,a,3).
point(real,b,100).
line(a,b,3).
point(real,c,105).
line(b,c,1).
point(real,d,-85).
line(c,d,1).
Taking into account the uncertainty in direction
and length, we can easily see that it will be
impossible to recognize directly the corner i as the
corner a, therefore it will be seen as a different one
and the robot will give infinite loops around the
room. This process will end when the following
module, the hybrid shape pattern matching, proposes
that corner a is corner i, so the shape is totally
explored.
1
2
3 4
Figure 1: An example of scenario.
b
a
c
d
e
f
g
h
i
j
Figure 2: The scenario map as build by the wall following process alone.
COOPERATIVE MAP BUILDING USING QUALITATIVE REASONING FOR SEVERAL AIBO ROBOTS
231
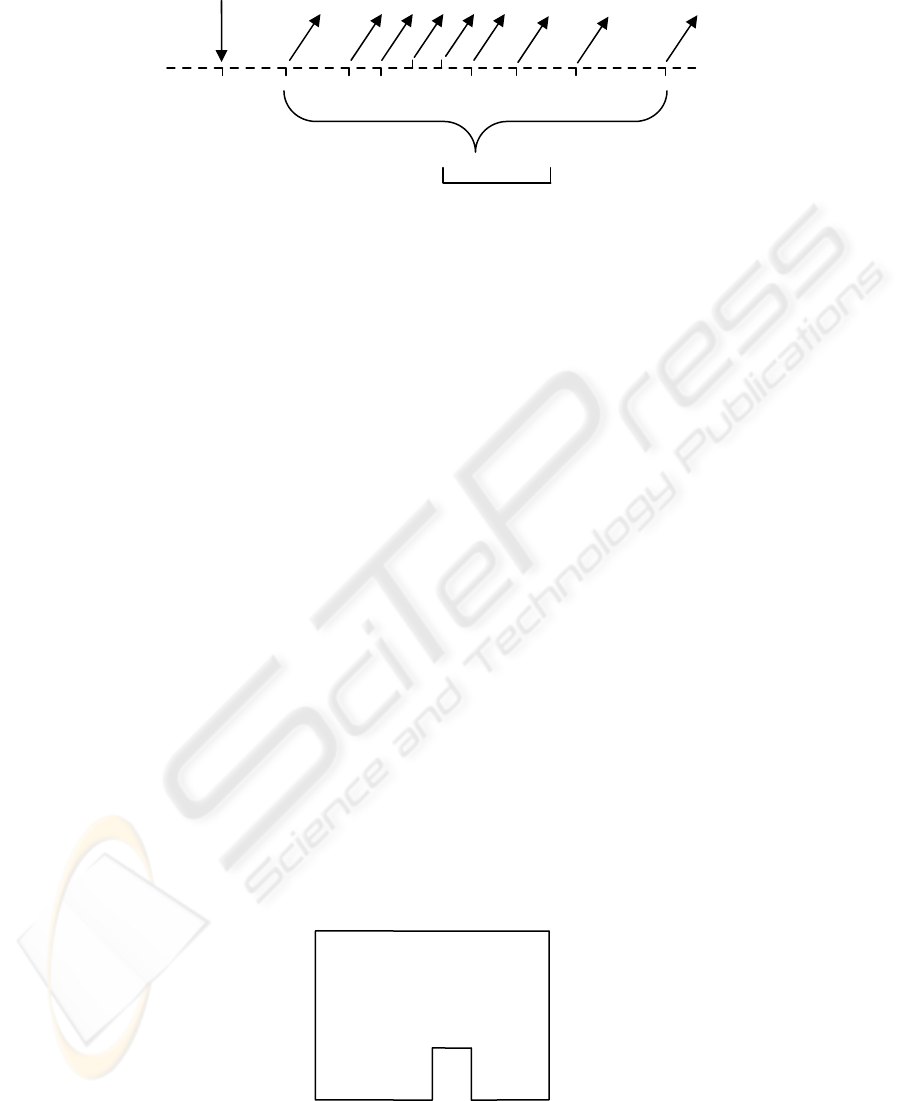
3.3 Hybrid Shape Pattern Matching
The hybrid shape pattern matching is continuously
monitoring the output of the previous module, which
can be seen in figure 3. In this figure, we can see
from left to right the movements of the robot, as a
straight line for each straight step, an angle down for
inner corners, and an angle up for external corners.
The pattern matching process tries to detect cycles in
the trace shown in figure 3. The first hypothesis
which we can make is to suppose that corner a is the
same as corner i, but the pattern matching process is
only sure when corner d is revisited, as is one of the
two only external corners of the scenario, and it is
very difficult to misrecognize this.
Note that this hypothesis can be wrong,
therefore it will be stated and maintained only if
subsequent measures are compatible with this
hypothesis. If not, the hypothesis must be revised
through a truth maintenance process which we
implement thanks to the backtracking mechanism of
prolog, the language we have implemented this
algorithm.
Once the hypothesis has been stated, the
scenario map is corrected under the assumption that
corner a is corner i, and the position and orientation
error between i and a, is cancelled by splitting it in
several minor corrections to angles and distances in
order to achieve that point a and point i will be the
same, resulting in a map as the one seen in figure 4.
3.4 Inner/Outer Area Exploration
Once the shape of the scenario has been resolved, it
is necessary to see if it is a shape enclosing the
robot, or if it is a shape surrounded by the robot.
This can be seen by simply seeing if the total angle
is +360 degrees, in which case the robot is inside the
shape, or -360 degrees, if the robot has surrounded a
shape from the outside. Now it is necessary to split
all the unexplored area by using the two-dimensional
qualitative orientation model of (Zimmerman and
Freksa, 1993). The model defines a Reference
System (RS) formed by two points, a and b, which
establishes the left/right dichotomy. The fine RS
includes two perpendicular lines by the points a and
b. This RS divides the space into 15 qualitative
regions (Figure5a). An iconical representation of the
fine RS and the names of the regions are shown in
Figure 5b).
obstacle
cycle i=a
a b c d e f g
h
i
Figure 3: The hybrid pattern matching process.
b=j
a=i
c
d e
f
g
h
Figure 4: The scenario map corrected by the hypothesis a=i.
ICINCO 2006 - ROBOTICS AND AUTOMATION
232

lf sf rf
l idf r
lm sm rm
ibl ib ibr
bl sb br
a) b)
Figure 5: a) The fine RS and b) its iconical representation.
The information which can be represented by
this RS is the qualitative orientation of a point
object, c, with respect to (wrt) the RS formed by the
point objects a and b, that is, c wrt ab. The
relationship c wrt ab can also be expressed in other
five different ways: c wrt ba, a wrt bc, a wrt cb, b
wrt ac and b wrt ca, which are the result of applying
the inverse (INV), homing (HM), homing-inverse
(HMI), shortcut (SC), and shortcut-inverse (SCI)
operations, respectively.
The composition of relationships for this model,
what we call Basic Step of the Inference Process
(BSIP), on qualitative spatial orientation is defined
such that “given the relationships c wrt ab and d wrt
bc, we want to obtain the relationship d wrt ab”.
The idea is to split the unexplored area in
several subareas where the position of the robot does
not vary with respect to any pair of corners of the
scenario shape. As there are many subdivisions,
secondly, we select not all, but only a few, which
makes all the subareas convex, and which
maximizes the probability of recognizing the corner
(for instance, corners d and e will be preferent). In
our case, the whole area is splitted in three convex
regions: abcd, dahe, and fehg. Then the robot starts
walking along the borders of these regions (lines a-d
and e-h).
If the robot found a wall while exploring the
area, the shape is explored by using the same
procedure of wall following and hybrid pattern
matching. If not, the subareas are finally explored
until the map is complete, or until the cooperative
map building process decides that the integrated map
is complete and that the individual maps must not be
completed, as it would result in duplication of effort.
4 MAP SHARING AND
SELF-LOCALIZATION
Each robot builds its own map independently
according to the procedure stated in the previous
point. In this point, which is made concurrently with
the previous one, each robot shares its individual
map with the other robots, so each robot has a copy
of the maps of the other ones. The objective is that
each robot must self-localize itself in the maps of the
other robots.
The procedure is very similar to the problem of
SLAM (Simultaneous Localization and Map
Building problem), which is described in (Lu, 1997).
In the SLAM problem, a mobile robot must explore
an unknown environment and to build a map of the
environment. Once the map is built, the robot is
kidnapped and located in other place of the
labyrinth. The robot must then be able to localize
itself in its map. A solution for this problem, making
use of an hybrid approach very close to the one we
describe, is described in (Escrig, 2005).
The key problem of the SLAM, which is the
same of this point, is to localize the robot in a map
already built. Is not important if the robot must
localize itself in a map of the environment made by
itself, or made by other robot.
The hybrid map of the environment,
corresponding to the exploration of figure 1, will be
the following (from point a to e):
point(real,a,95).
point(real,b,100).
line(a,b,3).
point(real,c,105).
line(b,c,1).
rel(a,b,c,[r]).
point(real,d,-85).
line(c,d,1).
rel(b,c,d,[r]).
point(real,e,-90).
line(d,e,1).
rel(c,d,e,[l]).
Where the predicate rel(a,b,c,[r]) means that the
qualitative orientation c wrt ab is r (see figure 5).
The process of self-localization of the robot in
the maps of others robots takes into account the own
map of each robot, and the fact that the robot is
localized in this map. Then the map of each robot is
compared with the maps of other robots, first by
comparing the qualitative orientation of the corners
(In the above example, the rel/4 predicate, which
says to us that the corner c is located at the right [r]
of system ab, that corner d is located at the right [r]
of system bc, and so on). The comparison of the
qualitative orientations is very simple in
computational cost and gives a few possibilities of
matching, which are then compared quantitatively
by using the line/3 and the point/3 predicates, which
allow us to compare the angles and distances, and
then the better matching is selected.
a
b
COOPERATIVE MAP BUILDING USING QUALITATIVE REASONING FOR SEVERAL AIBO ROBOTS
233

A simplification of this process is when a robot
detects another one, because then it is possible to
take advantage of the fact that two maps must match
exactly starting from the localization of their robots,
thus making simpler this process.
5 INTEGRATED MAP BUILDING
The last point is to integrate all maps in a single
map. This process can be done starting from the
individual maps and the matching corners that have
been identified in the previous point. This allows to
assert as working hypothesis (which can be wrong,
so this point must take into account a possible
backtracking of matching points) an integrated map
and the matching of each individual map in the
cooperative map. This hypothesis is maintained until
a robot generates a individual map which does not
match with the integrated map, resulting in a
backtracking process to detect which corner
matching is erroneous, according to new data. This
is a constraint solving problem, in which we offer
the integrated map as the map which better adjusts to
each individual map, but taking into account that is
not the only solution (for example, a solution where
the environment is composed of all individual maps
without any matching is always possible, but is not
the simpler one). A good way to select the working
hypothesis is to select the integrated map with fewer
corners of all solutions, compatible with current
matchings.
Finally, the integrated map building process
must decide if the integrated map is complete. If it
is, it will send a signal to all robots to make them
interrupt its individual map building process and to
accept the integrated map as complete, and to give
the environment as completely explored. If we do
not take this step, each robot will individually
explore the environment, so the exploring work
would be repeated as many times as robots we have,
and the idea is to accelerate the environment
exploration by using more robots.
6 CONCLUSIONS
This paper describes a procedure to the problem of
exploring a unknown environment with several
robots, which makes the exploration faster as the
number of robots increases. This is a good procedure
for starting cooperative works with several mobile
robots, as for example to explore an area for finding
things, or for vacuum cleaning of huge surfaces (as
commercial centres), and so on. The algorithm can
be programmed in a main host connected by
wireless with the mobile robots, or can be
implemented in each robot without a central host
(useful for autonomous systems), if a common
memory is shared among them by wireless.
Currently we are working on its implementation on a
team of Sony AIBO four legged robots, on an
unknown environment composed of boxes on a
room, to form a labyrinth which must be explored.
AKNOWLEDGEMENTS
This work is partly supported by the Spanish CICYT
project TIC 2003-07182.
REFERENCES
Lu, F., Milios, E., 1997. Globally consistent range scan
alignment for environment mapping. In Autonomous
Robots, 4:333-349.
Levitt, T.S., Lawton, D.T., 1990. Qualitative Navigation
for Mobile Robots, In AI, Vol. 44, 305-360.
Kuipers, B., 1978. Modelling Spatial Knowledge, In
Cognitive Science, 2, 129-153.
Freksa, C., Moratz, R., and Barkowsky, T., 2000.
Schematic maps for robot navigation. In C. Freksa, W.
Brauer, C. Habel & K. F. Wender (Eds.), Spatial
Cognition II – Integrating abstract theories, empirical
studies, formal models, and practical applications (pp-
100-114), Berlin: Springer.
Moravec, H.P., and Elfes, A., 1985. High Resolution Maps
from Wide Angle Sonar. In Proc. IEEE Int’l. Conf.
Robot. and Automat., St Louis, 116-121.
Thrun, S., Fox, D., Burgard, W., Dellaert, F., 2001. Robust
Monte Carlo localization for mobile robots. In
Artificial Intelligence 128 (299-141), Elsevier.
Thrun, S., 2002. Robotic mapping: A survey. In
G.Lakemeyer and B. Nebel, editors, Exploring
Artificial Intelligence in the New Millenium. Morgan
Kaufmann.
Thrun, S., 1998. Learning Metric-Topological Maps for
Indoor Mobile Robot Navigation. In Artificial
Intelligence, Vo. 99, No. 1, 21-71.
Escrig, M.T., and Peris, J.C., 2005. The use of a reasoning
process to solve the almost SLAM problem at the
Robocup legged league, IOS-Press, Catal. Conference
on Artificial Intelligence, CCIA’05, Oct. 2005.
Zimmermann, K., and Freksa, C., 1993. Qualitative spatial
reasoning using orientation, distance, and path
knowledge. Proc. Of the 13
th
Inter Joint Conf. on AI
Workshop on Spatial and Temporal Reasoning.
ICINCO 2006 - ROBOTICS AND AUTOMATION
234
