
MULTIPLE MOBILE ROBOTS MOTION-PLANNING: AN
APPROACH WITH SPACE-TIME MCA
Fabio M. Marchese
Dipartimento di Informatica, Sistemistica e Comunicazione
Universit
`
a degli Studi di Milano - Bicocca
Via Bicocca degli Arcimboldi 8, I-20126, Milan (Italy)
Keywords:
Mobile Robots, Motion Planning, Cellular Automata, Trajectories Generation.
Abstract:
In this paper is described a fast Path-Planner for Multi-robot composed by mobile robots having generic
shapes and sizes (user defined) and different kinematics. We have developed an algorithm that computes the
shortest collision-free path for each robot, from the starting pose to the goal pose, while considering their
real shapes, avoiding the collisions with the static obstacles and the other robots. It is based on a directional
(anisotropic) propagation of attracting potential values in a 4D Space-Time, using a Multilayered Cellular
Automata (MCA) architecture. This algorithm makes a search for all the optimal collision-free trajectories
following the minimum valley of a potential hypersurface embedded in a 5D space.
1 INTRODUCTION
In this paper we describe a safe path-planning tech-
nique for multiple robots based on Multilayered Cel-
lular Automata (MCA). The aim is to design a Co-
ordinator for multi-robot systems which decides the
motions of a team of robots while interacting with the
environment and reacting as fast as possible to its dy-
namical events. Many authors have proposed differ-
ent solutions during the last twenty-five years, based,
for example, on a geometrical description of the en-
vironment (e.g. (Lozano-P
´
erez and Wesley, 1979;
Lozano-P
´
erez, 1983)). The path-planners working on
these types of models generate very precise optimal
trajectories and can solve really difficult problems,
also taking into account non-holonomic constraints,
but they are very time consuming, too. In our opin-
ion, to face a real dynamical world, a robot must con-
stantly sense the world and re-plan accordingly to the
new acquired information. Other authors have de-
veloped alternative approaches less precise, but more
efficient: the Artificial Potential Fields Methods. In
the eighties, Khatib (Kathib, 1985) first proposed this
method for the real-time collision avoidance problem
of a manipulator in a continuous space. Jahanbin
and Fallside first introduced a wave propagation al-
gorithm in the Configuration Space (C-Space) on dis-
crete maps (Distance Transform (Jahanbin and Fall-
side, 1988)). In (Barraquand et al., 1992), the au-
thors used the Numerical Potential Field Technique
on the C-Space to build a generalized Voronoi Dia-
gram. Zelinsky extended the Distance Transform to
the Path Transform (Zelinsky, 1994). Tzionas et al.
in (Tzionas et al., 1997) described an algorithm for
a diamond-shaped holonomic robot in a static envi-
ronment, where they let a CA to build a Voronoi Dia-
gram. In (Warren, 1990) is proposed the coordination
of robots using a discretized 3D C-Space-Time (2D
workspace and time) for robots with the same shape
(only square and circle) and a quite simple kinematics
(translation only). La Valle in (LaValle and Hutchin-
son, 1998) applies the concepts of the Game Theory
and multiobjective optimization to the centralized and
decoupled planning. A solution in the C-Space-Time
is proposed in (Bennewitz et al., 2001), where the au-
thors use a decoupled and prioritized path planning
in which they repeatedly reorder the robots to try to
find out a solution. It can be proofed that these ap-
proaches are not complete. In this paper, we have
used CA as a formalism for merging a grid model of
the world (Occupancy Grid) with the C-Space-Time
of multiple robots and Numerical (Artificial) Poten-
tial Field Methods, with the purpose to give a simple
and fast solution for the path-planning problem for
multiple mobile robots, in particular for robots with
different shapes and kinematics. This method uses a
directional (anisotropic) propagation of distance val-
ues between adjacent automata to build a potential hy-
398
Marchese F. (2006).
MULTIPLE MOBILE ROBOTS MOTION-PLANNING: AN APPROACH WITH SPACE-TIME MCA.
In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 398-403
DOI: 10.5220/0001218103980403
Copyright
c
SciTePress

persurface embedded in 5D space. Applying a con-
strained version of the descending gradient on the hy-
persurface, it is possible to find out all the admissible,
equivalent and shortest (for a given metric of the dis-
cretized space) trajectories connecting two positions
for each robot C-Space-Time.
2 PROBLEM STATEMENTS
A wide variety of world models can be used to de-
scribe the interaction between an autonomous agent
and its environment. One of the most important is the
Configuration Space (Latombe, 1991; Lozano-P
´
erez,
1983). The C-Space C of a rigid body is the set of all
its configurations q (i.e. poses). If the robot can freely
translate and rotate on a 2D surface, the C-Space is a
3D manifold R
2
× SO(2). It can be modelled using
a 3D Bitmap GC (C-Space Binary Bitmap), a regular
decomposition in cells of the C-Space, represented by
the application GC : C → {0, 1}, where 0s represent
non admissible configurations. The C-Potential is a
function U(q) defined over the C-Space that ”drives”
the robot through the sequence of configuration points
to reach the goal pose (Barraquand et al., 1992). Let
us introduce some other assumptions: 1) space topol-
ogy is finite and planar; 2) the robot has a lower bound
on the steering radius (non-holonomic vehicle). The
latter assumption introduces important restrictions on
the types of trajectories to be found.
Cellular Automata are automata distributed on the
cells of a Cellular Space Z
n
(a regular lattice) with
transition functions invariant under translation (Goles
and Martinez, 1990): f
c
(·) = f (·), ∀c ∈ Z
n
, f (·) :
Q
|A
0
|
→ Q, where c is the coordinate vector identi-
fying a cell, Q is the set of states of an automaton and
A
0
is the set of arcs outgoing from a cell to the neigh-
bors. The mapping between the Robot Path-Planning
Figure 1: MultiLayers Architecture.
Problem and CA is quite simple: every cell of the
C-Space Bitmap GC is an automaton of a CA. The
state of every cell contributes to build the C-Potential
U(q) through a diffusion mechanism between neigh-
bors. The trajectories are found following the mini-
mum valley of the surface U(q). In this work, we use
a simple extension of the CA model: we associate a
vector of attributes (state vector) to every cell. Each
state vector depends on the state vectors of the cells
in the neighborhood. There is a second interpretation:
this is a Multilayered Cellular Automaton (Bandini
and Mauri, 1999), where each layer corresponds to
a subset of the state vector components. Each sub-
set is evaluated in a single layer and depends on the
same attribute of the neighbor cells in the same layer
and depends also on the states of the corresponding
cell and its neighbors in other layers. In the follow-
ing sections, we describe each layer and the transition
function implemented in its cells.
3 MULTILAYERED
ARCHITECTURE
In Fig. 1 is shown the layers structure and their de-
pendencies. There are two main layers: Obstacles
Layer and the Attraction Layer. Each layer is sub-
divided in more sublayers: the Obstacles L. has 3 di-
mensions (2 for the workspace (X, Y ) and 1 more for
the time), while the Attraction L. has up to 5 dimen-
sions (1 for the robots, 2 for the robots workspaces +
1 for their orientations (X, Y, Θ) and 1 for the time).
In the following subsections, we will briefly describe
each layer and their roles. The Obstacles L. concep-
tually depends on the outside environment. Its sub-
layers have to react to the ”external” changes: the
changes of the environment, i.e. the movements of
the obstacles in a dynamical world. Through a sen-
sorial system (not described here), these changes are
detected and the information is stored in Obstacles L.
permitting the planner to replan as needed.
3.1 The Obstacles Layer
The main role of the Obstacles Layer is to create a re-
pulsive force in the obstacles to keep the robots away
from them. In the present work, only static obstacles
are considered (e.g. walls). For the single robot, the
other robots are seen as moving obstacles, with un-
known and unpredictable trajectories. We are consid-
ering a centralized planner/coordinator, that can de-
cide (and, of course, it knows) the trajectories of all
the supervised robots. Thanks to this knowledge, the
planner considers the silhouette of the robot as an ob-
stacle for the other robots. In this work, we introduce
a discretized version of the C-Space-Time as in (War-
ren, 1990). With the introduction of the Time axis,
MULTIPLE MOBILE ROBOTS MOTION-PLANNING: AN APPROACH WITH SPACE-TIME MCA
399
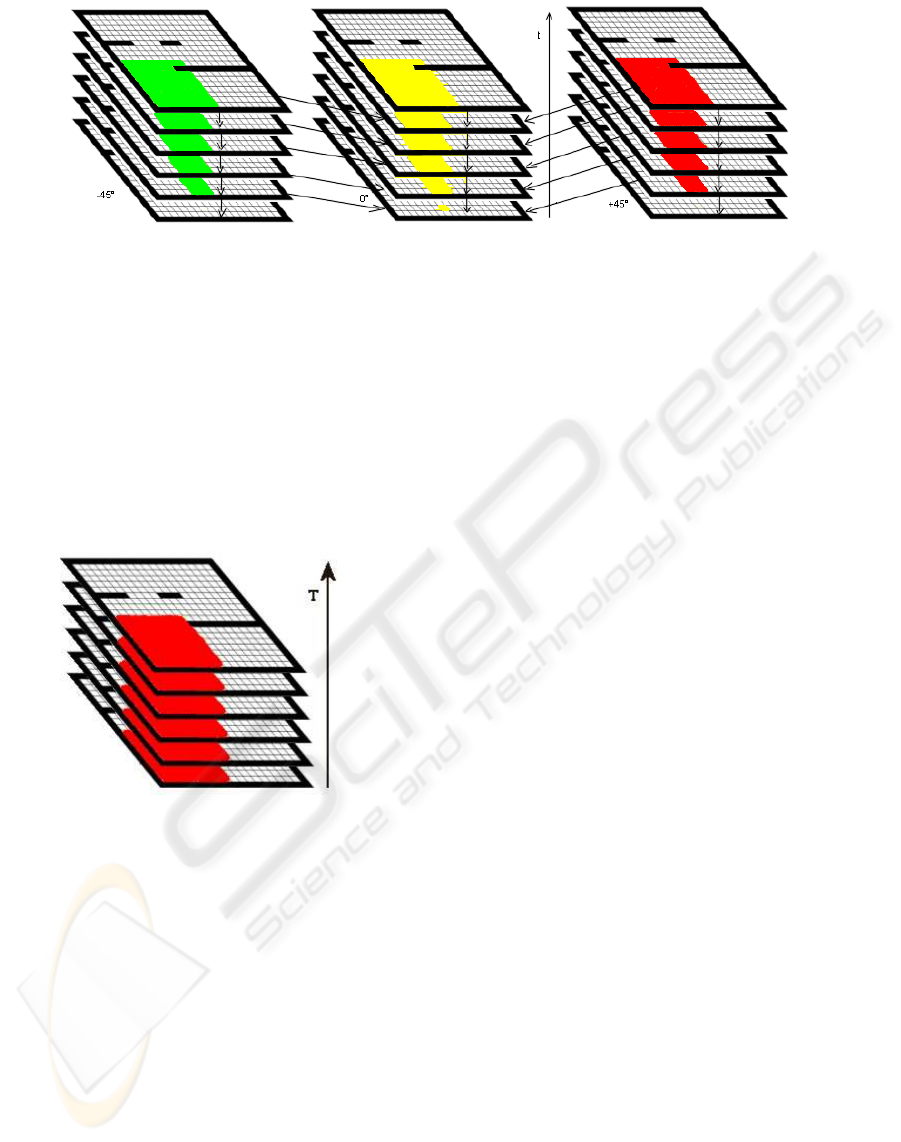
Figure 2: Dependencies between Attractive Layers at different orientations.
the robots moving in the environment become ”static”
obstacles in the Space-Time 4D space, having differ-
ent poses in each time slice. We can still call them as
C-Obstacles, remembering that they are extended in
the time dimension. In our case, we have a 3D Space-
Time: R
2
×R, where R
2
is the planar workspace. The
overall ”static” space-time obstacle, representing one
robot, is the composition of all the robot silhouettes
in each time slice (Fig. 3). The time step (slice) is the
Figure 3: Discretized C-Space-Time and C-Obstacles.
time needed by a robot to move to an adjacent cell, if
we consider all the robots moving at the same speed
(the robots motions are synchronized). This layer is
also called Coordination Layer (Space) because the
motion of all the robots are coordinated in this layer
(see 3.3).
3.2 The Attractive Layer
The Attractive Layer is the core of the algorithm. It
computes the shortest collision-free path for a single
robot, from the starting pose to the goal pose, while
considering its real occupation (shape and size = sil-
houette). To pass from one cell to an other one, the
robot can follow different paths, combining different
atomic moves, such as strict forward move, diagonal
move, rotation, and so on. Each move has its own cost
(always positive); the entire set of admissible move-
ments define the robot kinematics. The planner is able
to handle at the same time different type of robots,
with different shapes, sizes and kinematics (e.g. car-
like kinematics, omnidirectional, etc.), providing for
each one the proper trajectory. In this work, the moves
are space-temporal, i.e. every time the robot moves
in the space, it also moves in the time. Even when
the robot stands in the same place, it moves (verti-
cally) in the space-time (also this particular move has
its own cost). The moves costs are used to build in-
crementally a potential surface starting from the goal
cell, placed at a high time slice (the desired time of
arrival), and expanding it in all the free space-time. In
our case, it is a hypersurface embedded in a 4D space:
R
2
× SO(1) × R, where R
2
is the workspace, en-
larged with the robot orientation dimension (SO(1))
and the time. The goal cell receives the first value
(a seed), from which a potential bowl is built adding
the cost of the movement that would bring the robot
from a surrounding cell to it. The calculus is per-
formed by the automata in the space-time cell, which
computes the potential value depending on the poten-
tial values of the surrounding space-time cells. Iter-
ating this process for all the free cells, the potential
surface is built leaving the goal cell with the mini-
mum potential. The potential value has a particular
mean: it is the total (minimal) cost needed to reach
the goal from the current cell. Because the costs are
positive, no other minimum is generated, thus avoid-
ing the well-known problem of the ”local minima”.
The entire trajectory is computed just following the
direction of the negated gradient of the surface from
the starting point. The path results to be at the mini-
mum valleys of the surface. Every robots have differ-
ent goals and kinematics, hence a potential bowl for
each one has to be generated separately. The potential
bowl is built only in the free space, avoiding to enter
in the C-Obstacles areas. Therefore, the robot Attrac-
tive Layer depends on the Obstacles Layer. The last
one embeds the Time, thus the potential bowl varies
with the time, generating different potential surfaces
ICINCO 2006 - ROBOTICS AND AUTOMATION
400
at different starting time and, consequently, different
trajectories. In Fig. 2 is shown the dependencies be-
tween Layers and Sublayers of the overall Attractive
Layer. Each sublayer, at a given robot orientation,
depends on the adjacent sublayers at different orien-
tations (aside in the figure), and depends also on the
below temporal sublayer.
3.3 The Planning Algorithm
Entailing the layer structure previously introduced, is
now possible to describe the algorithm to compute the
robots trajectories. The first step is to establish the
robots priorities. Up to now, no heuristic has been
found and the assignment is casual. The following
step is to initialize the Obstacles Layer with the ob-
stacle distribution known from the Occupancy Map
of the workspace. Each temporal sublayer is set to the
Occupancy Map (full if the cell has an obstacle inside,
empty otherwise). Then, the algorithm computes the
Attractive Layer of the robot with the highest prior-
ity level based on the Obstacles Layer. Setting the
minimum potential value to the goal cell, it makes the
potential bowl growing while surrounding the obsta-
cles. Knowing the potential surface, it extracts the
shortest path, following the negated gradient from the
starting cell. For each passing points, then it adds the
robot silhouettes, properly oriented, in each tempo-
ral sublayer of the Obstacles Layer. In this way, the
first robot becomes a space-time ”obstacle” for the
successive robots, with lower priorities. The Obsta-
cles Layer has a central role in this phase, because it
ensures that the robots avoid each other and the tra-
jectories do not intersect each other, even taking into
account their real extensions. For this reason, in this
context it is also called Coordination Space. The next
phase is to repeat the procedure for the second robot,
starting to build its Attractive Layer on the base of the
modified Obstacles Layer, and then adding to it all its
silhouettes at each time-stamp. The algorithm termi-
nates when it has computed all the robots trajectories.
4 EXPERIMENTAL RESULTS
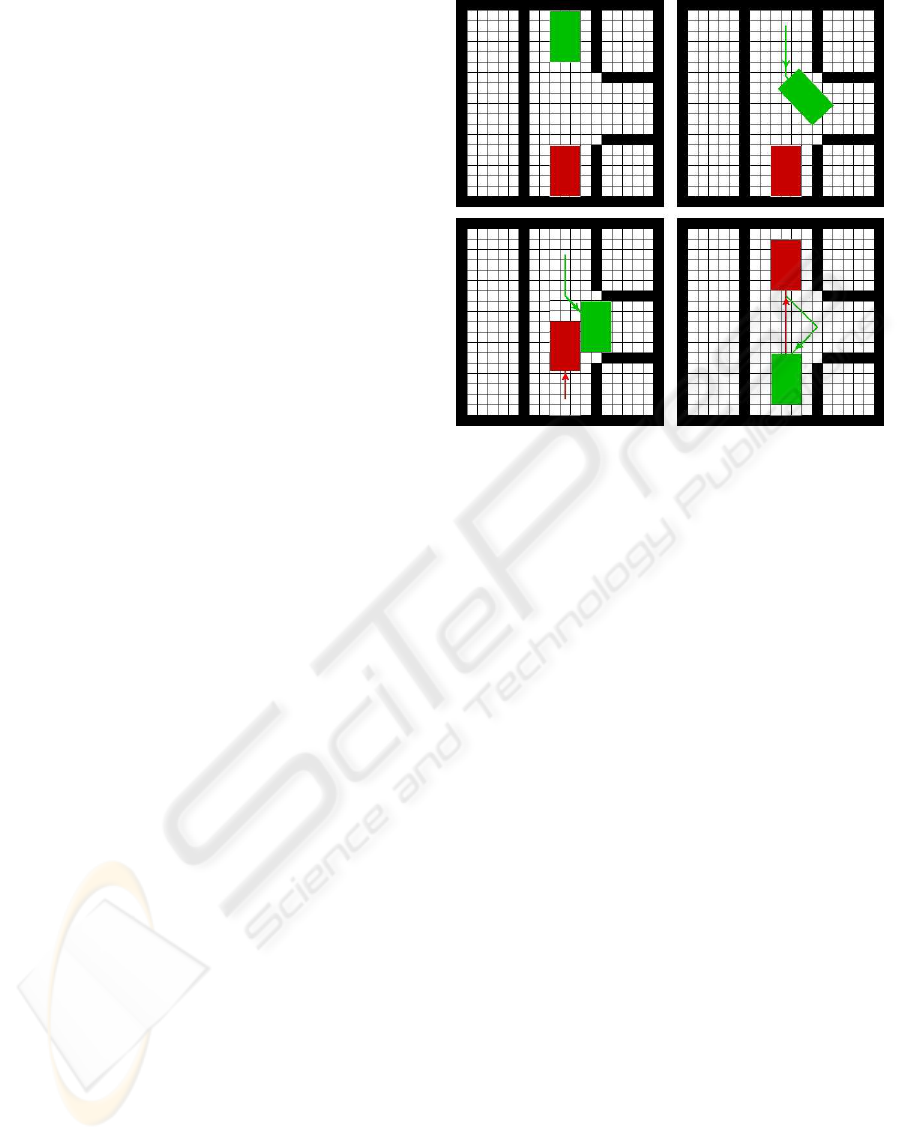
The priority planning is not complete: there are situ-
ations for which there is a ”natural” simple solution,
but this type of algorithm is not able to find it. In
Fig. 4 is shown an example (a similar one in (Ben-
newitz et al., 2001)) of such a type of problems and
a simple solution. Adopting a priority order (e.g. the
green robot moves before the red one) there is no solu-
tion. Because this problem is symmetric, even swap-
ping the priority order (e.g. the red one passes before
the green one) there is still not a solution with a prior-
Figure 4: Counter-example: a situation for which the prior-
ity planning does not find a solution.
ity schema. Fortunately, for most of the situations we
do not have this kind of problem and the algorithm
finds a solution. In the example of Fig. 5, the red
robot has the clear the way to permit the green one
to get out of the room, then it gets back to the orig-
inal position. The following example (Fig. 6) shows
a classical problem where the robots trajectories have
to cross to exchange their positions in the four cor-
ners. In the middle of the environment there is a con-
flict zone where all the robots have to pass. All the
robots start contemporarily, but the red and yellow
robots have to stop to permit the blue and the green
robots (with higher priority levels) to pass. Then also
the red and yellow ones complete their paths.
5 CONCLUSIONS
In this paper we have proposed a decoupled and pri-
oritized path planning algorithm for coordinating a
Multi-Robot composed by mobile robots using a Mul-
tilayered Cellular Automata. One of the main topics is
that we face contemporarily with mobile robots hav-
ing generic shapes and sizes (user defined) and differ-
ent kinematics. It is based on the Priority Planning ap-
proach in the C-Space-Time where the Time has been
added to the normal C-Space. The Priority Planning
is not complete, but it works very well for most of
the problems, finding all the collision-free equivalent
paths for each robot. The algorithm is also able to
manage the robots orientations, avoiding to waste a
lot of space during the motion, and permitting to find
MULTIPLE MOBILE ROBOTS MOTION-PLANNING: AN APPROACH WITH SPACE-TIME MCA
401
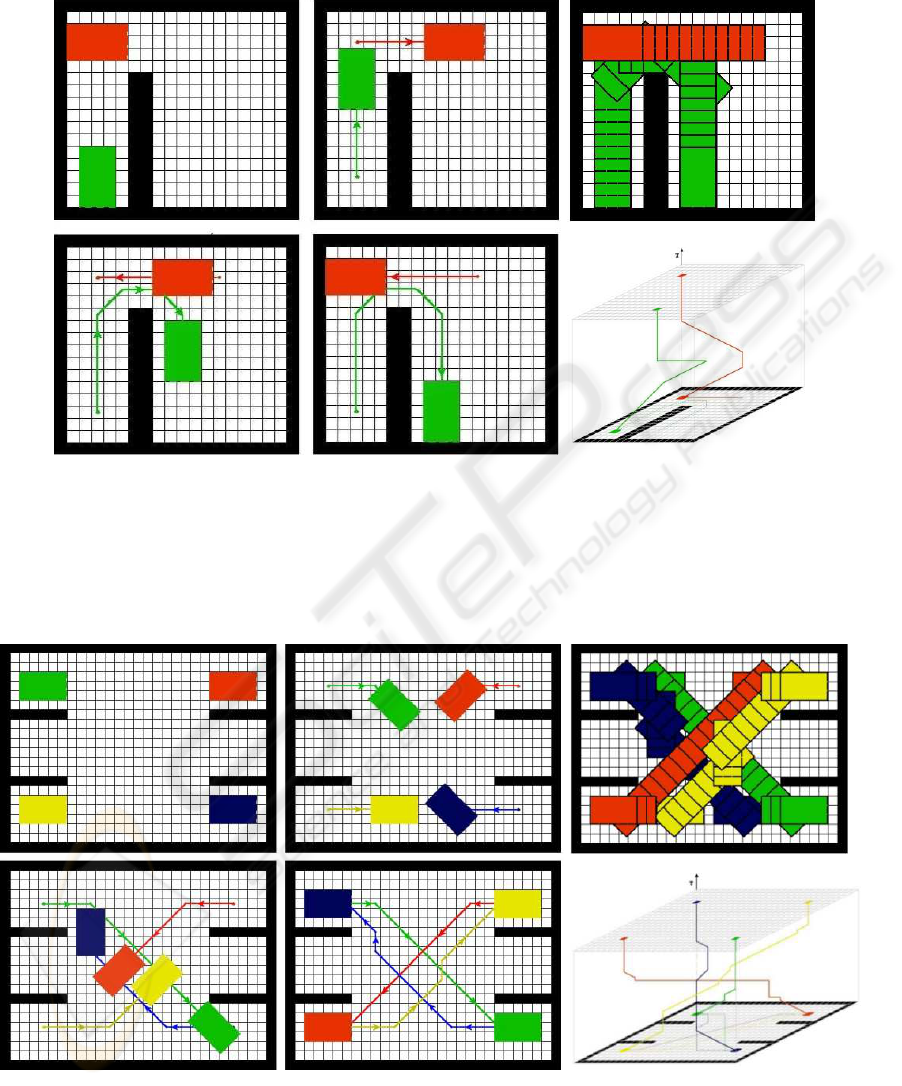
Figure 5: Robot clearing the way: a snapshots sequence (four frames on the left); the overall movements and C-Space-Time
movements.
Figure 6: Crossing robots: a snapshots sequence (four frames on the left); the overall movements and C-Space-Time move-
ments.
ICINCO 2006 - ROBOTICS AND AUTOMATION
402

paths in cluttered workspaces. The trajectories found
are smoothed and respect the kinematics constraints
of each robot.
ACKNOWLEDGEMENTS
The author wish to thank Dott. Marco Dal Negro for
the contributions given with his Graduate Thesis.
REFERENCES
Bandini, S. and Mauri, G. (1999). Multilayered cellular au-
tomata. Theoretical Computer Science, 217:99–113.
Barraquand, J., Langlois, B., and Latombe, J. C. (1992).
Numerical potential field techniques for robot path
planning. IEEE Trans. on Systems, Man and Cyber-
netics, 22(2):224–241.
Bennewitz, M., Burgard, W., and Thrun, S. (2001). Op-
timizing schedules for prioritized path planning of
multi-robot systems. In IEEE Int. Conf. on Robotics
and Automation (ICRA), Seoul (Korea).
Goles, E. and Martinez, S. (1990). Neural and Au-
tomata Networks: dynamical behavior and applica-
tions. Kluwer Academic Publishers.
Jahanbin, M. R. and Fallside, F. (1988). Path planning us-
ing a wave simulation technique in the configuration
space. In Artificial Intelligence in Engineering: Ro-
botics and Processes (J. S. Gero ed.), Southampton.
Computational Mechanics Publications.
Kathib, O. (1985). Real-time obstacle avoidance for ma-
nipulator and mobile robots. In Int. Conf. on Robotics
and Automation.
Latombe, J. C. (1991). Robot Motion Planning. Kluwer
Academic Publishers, Boston, MA.
LaValle, S. M. and Hutchinson, S. A. (1998). Optimal
motion planning for multiple robots having indepen-
dent goals. IEEE Trans. on Robotics and Automation,
14(6):912–925.
Lozano-P
´
erez, T. (1983). Spatial planning: A configura-
tion space approach. IEEE Trans. on Computers, C-
32(2):108–120.
Lozano-P
´
erez, T. and Wesley, M. A. (1979). An algo-
rithm for planning collision-free paths among polyhe-
dral obstacles. Comm. of the ACM, 22(10):560–570.
Tzionas, P. G., Thanailakis, A., and Tsalides, P. G. (1997).
Collision-free path planning for a diamond-shaped ro-
bot using two-dimensional cellular automata. IEEE
Trans. on Robotics and Automation, 13(2):237–250.
Warren, C. (1990). Multiple robot path coordination us-
ing artificial potential fields. In Proc. of the IEEE
Int. Conf. on Robotics and Automation (ICRA), pages
500–505.
Zelinsky, A. (1994). Using path transforms to guide the
search for findpath in 2d. Int. J. of Robotics Research,
13(4):315–325.
MULTIPLE MOBILE ROBOTS MOTION-PLANNING: AN APPROACH WITH SPACE-TIME MCA
403
