AN ALGORITHM EVALUATION TEST SUITE FOR BLIND SOURCE

SEPARATION PROBLEM

Marina Charwath, Imke Hahn, Sascha Hauke, Martin Pyka, Slawi Stesny,

Dietmar Lammers, Steffen Wachenfeld and Markus Borschbach

Dept. of Mathematics and Natural Science, Institute for Computer Science

Einsteinstr. 62, D-48149 M

unster, Germany

Keywords:

Blind signal separation, automated evaluation, reference matlab based test engine and test data suite.

Abstract:

To ensure the integration and a systematic performance evaluation of the CubICA, the JADE and the EfICA

algorithm, a previously developed testsuite for BSS-problems is used. All the steps to perform a competition

of methods for source separation are part of a testsuite that supports the development and evaluation of blind

source separation (BSS) algorithms in a highly automated way. The concept of the testsuite is presented

and it is shown how the testsuite can be used to apply a selection of BSS-algorithms to four standard sub-

problems. To compare the performance of arbitrary algorithms on given problems the testsuite allows the

integration of new algorithms and testing problems using well deﬁned interfaces. A brief example is given by

the integration of the FlexICA, EVD, EVD24 and the FastICA. Also the integration of CubICA, JADE and the

EfICA algorithm and the results achieved from automated tests and parameter optimizations will be described

in comparison.

1 INTRODUCTION

Given that in the last decade, the interest in Blind Sig-

nal Separation for the application in various ﬁelds,

like processing of biomedical or geophysical data,

speech or image processing and wireless communi-

cation code recognition is growing steadily (refer to

(Cichocki, 2002), (Oja, 2001) for an introduction),

the development of new blind source separation algo-

rithms is accompanied by the constant need of eval-

uating and comparing the newly created algorithms

with existing ones. The comparison of algorithms in

an objective manner requires test conditions, such as

the test-problem itself and the performance measures,

to be ﬁxed. Furthermore, the quality of each algo-

rithm depends on the algorithm’s parameters and the

performed steps of pre-processing and noise-addition,

see (Giannakopoulos, 1998), (Dougla, 2005) for in-

stance. To address this, a MATLAB-based test-

suite was developed that allows an automated per-

formance comparison of different algorithms under

deﬁnable testing conditions. Combinations of pre-

processing steps such as PCA or high-/low-pass ﬁl-

tering and different noise models could be automat-

ically tested. For each combination the parameter

range of the algorithms can be searched for optima.

In order to determine optimum outcomes, different

performance measures can be used. In the next sec-

tion, the concept of the testsuite and how it can be

used for automated algorithm evaluation is presented

shortly. In section 3 the evaluation and comparison of

the seven algorithms is demonstrated, whereas they

were split up as follows: FlexICA (Cichocki, 2002),

EVD, EVD24 (Oja, 2001) and FastICA (Oja, 2001) in

one group and FlexICA, JADE (Cardoso, 1999), Cu-

bICA (Blaschke, 2003) and the EfICA (Koldovsky,

2005) in the other. The section as well contains the

achieved performance results of these algorithms for

the four sub-problems: (I.) Large scale problem, (II.)

Incomplete or reduced set data problem, (III.) Very

ill-conditioned problem (IV.) Noisy problem.

2 TESTSUITE

The generation of test-data and the application,

evaluation and comparison of algorithms is normally

performed in different stages. Accordingly, the

testsuite consists of multiple stages as shown in

ﬁgure 1. At each stage of the testsuite, interfaces

exist to allow for the addition of new signal mixing

methods, new pre-processing steps, different noise

186

Charwath M., Hahn I., Hauke S., Pyka M., Stesny S., Lammers D., Wachenfeld S. and Borschbach M. (2006).

AN ALGORITHM EVALUATION TEST SUITE FOR BLIND SOURCE SEPARATION PROBLEM.

In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 186-192

DOI: 10.5220/0001211301860192

 SciTePress

Figure 1: Stages of algorithm evaluation and comparison.

models, sample reduction methods, signal separation

algorithms and custom performance measures.

The different stages and the currently integrated mod-

ules/ functionalities at each stage will be described

brieﬂy in the following.

Generation stage

The generation stage consists of signal mixing and

noise addition modules. The signal mixing modules

allow to mix any number of independent sources S

according to the linear standard ICA model X = AS

(Borschbach, 1999) (Hagen, 1997). The testsuite

supports any sources in MATLAB vector format

and allows to synthetically generate sources or

import .wav audio ﬁles using an integrated dataset

creation tool. The mixing matrix A can be explicitly

given or randomly created. Furthermore, the use of

Hilbert matrices for any dimension is possible. Other

matrix creation methods can be added if needed.

At the generation stage the addition of noise can be

performed so that the mixing model is extended to

X = AS + N . The added noise N is generated

according to a noise model which is currently

selectable from Gaussian-noise, Uniform-noise and

Salt-and-Pepper-noise. For each noise model, the

number of affected samples can be adjusted and a

target signal to noise ratio (SNR) can be speciﬁed in

dB. Other noise models can easily be added if wanted.

Preparation stage

The preparation stage offers signal pre-processing

and sample reduction functionalities. Before ex-

ecuting the main signal separation algorithms the

application of pre-processing steps such as principal

component analysis (PCA) and signal ﬁltering is

possible. In addition to the currently implemented

low- and high-pass ﬁlters custom ﬁlters can be

easliy integrated. A windowing technique allows for

limiting the amount of considered data samples. Only

samples inside the window are used for blind signal

separation.

Separation stage

Within the separation stage the integrated blind

source separation algorithms are applied to the

generated and prepared data sets. The algorithms

can be called with different combinations of their

individually required parameters. The possibility to

call the algorithms with varied parameters allows

for systematical parameter testing and optimization.

Newly developed algorithms can be added in an easy

and comfortable way. A tutorial for developers on

how to integrate new algorithms into the application

is provided (Testengine, 2006).

Evaluation stage

The evaluation stage consists of performance mea-

suring and result representation functionalities. The

performance of algorithms is being determined

according to several measures, such as signal-to-

interference ratio (SIR) or intersymbol interference

(ISI, called Perform in the testsuite) (Schobben,

AN ALGORITHM EVALUATION TEST SUITE FOR BLIND SOURCE SEPARATION PROBLEM

187

1999). Further performance measures can be added

as required. Results are being presented primarily in

a tabular form, with other representations, such as

box plots (Oja, 1999), optionally available. As with

the other stages, further methods of presenting the

data can be integrated if needed. All test results can

automatically be written to a SQL database during

the test. This allows for data analysis with powerful

external tools.

Test Engine

The test engine controls all settings and parameters

passed to the modules during the test cycle. This helps

to ﬁnd optimal settings and parameters in a systematic

fashion. Several steps in determining the algorithms’

best performance are automated. These include pro-

gression of noise intensity and sample reduction.

Noise progression is done by successively increasing

the signal-to-noise ratio (SNR) and per cent amount

of noise of a mixture up to a maximum. Sample re-

duction is done by gradually decreasing the size of the

window used by the algorithms. This shows how the

algorithms’ performance is affected by random noise

or the amount of data available, respectively. Noise

progression and sample reduction are mutually exclu-

sive. Automation of parameter values are also inte-

grated into the test engine.

Results can be stored in a SQL database, as mentioned

before, as well as in .mat ﬁles for further performance

analysis during the test-cycle and between the steps.

This allows for the reduction of signal generation and

modiﬁcation to a single time and reusing the gener-

ated and preparated data with different algorithms.

This feature has been implemented using the MAT-

LAB database toolbox.

Finally, the test engine will generate a result report

showing the pertinent data. This includes options

to visualize the results, such as data sample plots of

source, mixed and unmixed data. Additionally, box-

plots of performance measures for the different algo-

rithms are supplied. This is done in order to improve

general comparability of different algorithms.

3 EVALUATION RESULTS

Using the developed testsuite, the following seven

algorithms have been tested: (I.) The FlexICA

algorithm, developed by S. Choi, A. Cichocki and S.

Amari (Cichocki, 2002), (II.) The EVD algorithm,

developed by P. Georgiev and A. Cichocki (Oja,

2001), (III.) The EVD24 algorithm, developed by

P. Georgiev and A. Cichocki (Oja, 2001), (IV.) The

FastICA algorithm, developed by J. Hurri, H. G

avert,

J. S

arel

a, and A. Hyv

arinen (Oja, 2001), (V.) JADE

algorithm, see J.-F. Cardoso (Cardoso, 1999), (VI.)

CubICA algorithm, see T. Blaschke and L. Wiskott

(Blaschke, 2003), (VII.) EFICA algorithm, see Z.

Koldovsky and P. Tichavsky (Koldovsky, 2005).

Using the testsuite to systematically try different

settings and parameter for the algorithms, a general

observation was, that high pass ﬁltering during the

pre-processing stage yielded better results than unﬁl-

tered or low pass ﬁltered data. Therefore all datasets

have been high pass ﬁltered before applying the re-

spective algorithms. All tests were performed on two

types of datasets: real world data and synthetically

created random non-negative source signals. We used

T=5000 samples. The synthetic datasets have been

created using the testsuite’s integrated data generation

module. All experiments were conducted in a Monte

Carlo fashion with at least 100 independent runs

using randomly generated mixing matrices. All of

these have been applied to the four sub-problems.

The results the algorithms yielded will be presented

in the following sections. All synthetic datasets have

been created using the testsuite’s integrated data

generation module. The ﬁgures given in the next

sections represent the mean values of the SIR over

at least 100 runs using randomly generated mixing

matrices. This was done to guarantee stable results in

a Monte Carlo fashion.

Large scale problem

The ﬁrst sub-problem deals with the algorithms’ per-

formance given an increasing dimension of the data

set. The data sets used for testing contain an equal

number of sub- and super-Gaussian sources, e.g. for

dimension 6 the data set would contain 3 sources of

each type. With increasing dimension the SIR drops,

as illustrated in the upper part of ﬁgure 2 for synthetic

data and in the lower part of ﬁgure 2 for real world

speech data. It can be noticed that the two EVD vari-

ants fare poorly compared to FastICA and FlexICA.

For synthetic data they are basically unable to sepa-

rate the mixtures. FastICA and FlexICA on the other

hand are performing better. Up to 20 sources can be

separated without the SIR falling below 15dB.

For real world data the algorithms perform better than

for the synthetic sources. This can probably be at-

tributed to the super-Gaussian nature of the signals.

For the comparison for the second algorithm group a

randomly generated proportion of sub-Gaussian and

super-Gaussian sources combined in one data set was

used, e.g. for dimension 4 the dataset would con-

tain either 2 sources of each type or 1 source of the

ﬁrst and 3 sources of the other type. As expected,

the SIR drops with increasing dimension (see upper

part of ﬁgure 3). It clearly appeared that the FlexICA

performs poorly compared to the others. The best of

these four algorithms, the EfICA algorithm, has an

decreasing SIR reaching the 15dB mark for more than

64 dimensions.

ICINCO 2006 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

188

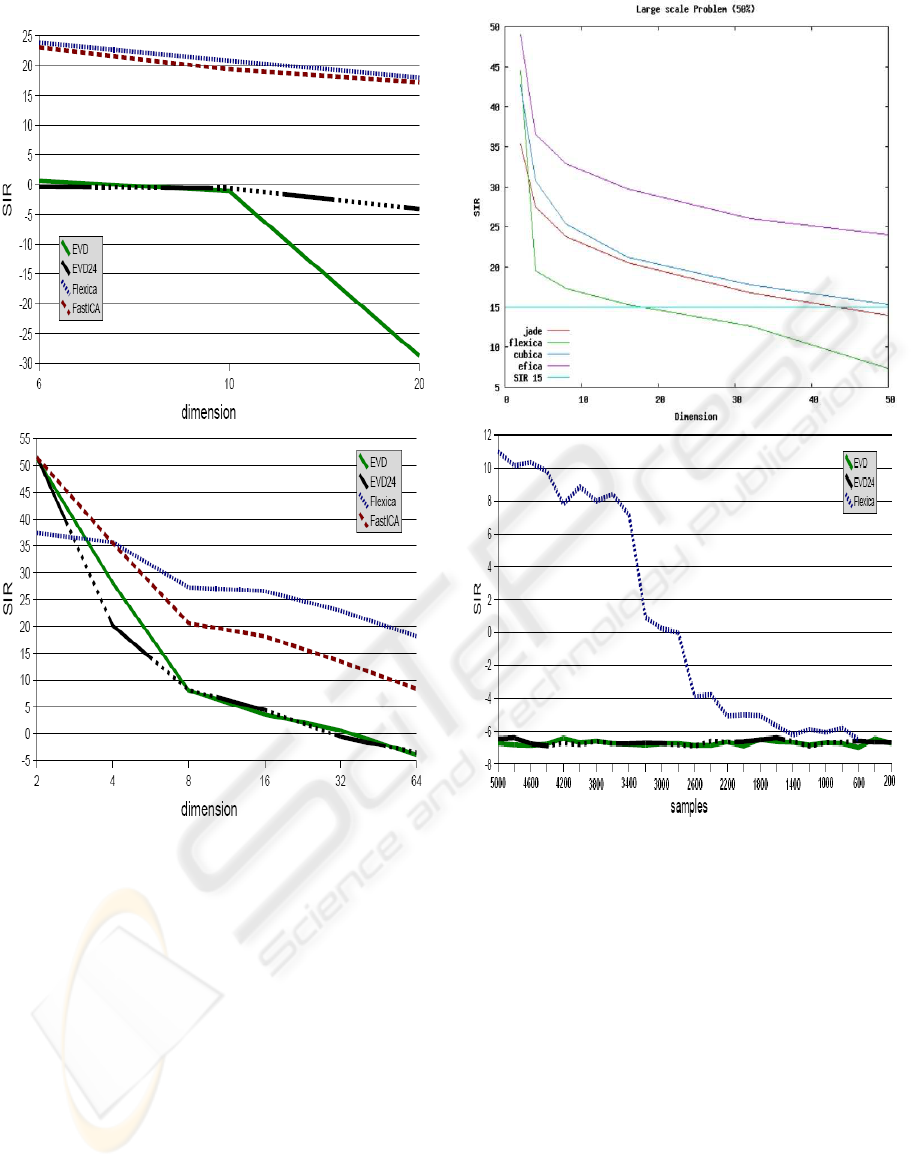
Figure 2: Upper part: SIR global performance index for

the large scale sub-problem 1 (set 2) using synthetic data.

Lower part: SIR global performance index for the large

scale sub-problem 1 (set 2) using real world speech data.

Incomplete or reduced set data problem

The second sub-problem is concerned with the

reduction of samples available to the algorithms. Al-

gorithmic performance in this task can be determined

using the test engine’s sample reduction feature. The

datasets are being reduced in length successively, the

algorithms attempt to estimate the inverse mixing

matrix using fewer samples each step. This is done

fully automated by the testsuite.

The lower part of ﬁgure 3 shows the performance

of the ﬁrst three algorithms trying to separate 50

synthetically generated sources of decreasing sample

count. FastICA was not able to complete this task

in a stable way and was therefore not included. The

Figure 3: Upper part: Global performance index for sub-

problem 1 and a SIR of 50%, Lower part: SIR global per-

formance index for the incomplete/ reduced dataset.

EVD variants were not able to successfully separate

any of the sources, and even the FlexICA algorithm

never reached a SIR > 15dB, even at full sample

count of 5000. The performance for real world data

is somewhat better for the FlexICA algorithm, as

displayed in the lower part of ﬁgure 4. Even with

only 3200 available samples it still reaches a SIR of

approximately 15dB. EVD and EVD24 show unusual

behavior, as their performance improves signiﬁcantly

beginning at 2800 samples. The cause of this has yet

to be determined. The lower part of ﬁgure 4 shows

the performance of four algorithms trying to separate

n=50 synthetically generated sources of decreasing

sample count. The FlexICA and the JADE algorithm

never reached a SIR > 15dB, even at full sample

count of T=5000. The CubICA just about reaches

AN ALGORITHM EVALUATION TEST SUITE FOR BLIND SOURCE SEPARATION PROBLEM

189

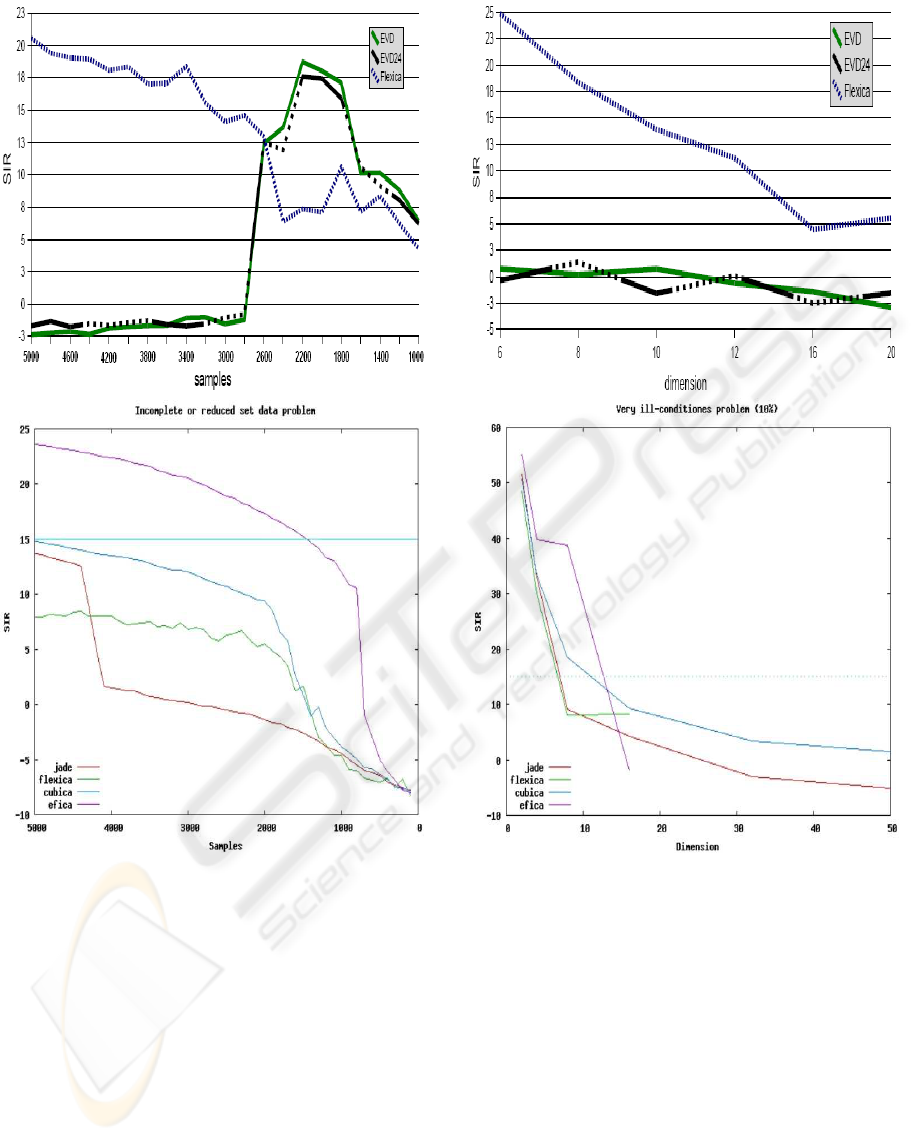
Figure 4: Upper part: SIR global performance index for the

incomplete/reduced sub-problem 2 (set 2) using real world

speech data. Lower part: SIR global performance index for

sub-problem 2.

the SIR > 15dB margin but only at full sample

count. Again the EfICA easily outnumbers all other

algorithms.

Very ill-conditioned problem

Sub-problem three uses Hilbert matrices in the

mixing process. Due to the nearly singular nature

of these matrices, inversion becomes more difﬁcult.

This is mirrored by the results given in the lower part

of ﬁgure 5 and the upper part of ﬁgure 5 . Among the

tested algorithms reported in the upper part of ﬁgure

5, only FlexICA manages to provide acceptable

results.

Figure 5: Upper part: SIR global performance index for

the very ill conditioned sub-problem 3 (set 1) using syn-

thetic data. Lower part: Global performance index for sub-

problem 3 and a SIR of 10%.

For low dimensions below ten sources, the SIR

is higher than the required 15dB. While this is

signiﬁcantly more than for the EVD variants, it still

is not a truly satisfactory performance. Overall these

results are congruent with those of the previous tests

and clearly show the inability of EVD to deal with

datasets comprised of both sub- and super-Gaussian

sources. For the simulation of the ICA-algorithm

competition (illustrated in the lower part of ﬁgure 5)

in case of FlexICA and EfICA, the condition of the

mixing matrices could not be calculated accurately

for each data matrix/ dimensionality. It should

be mentioned that both the FlexICA and EfICA

ICINCO 2006 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

190

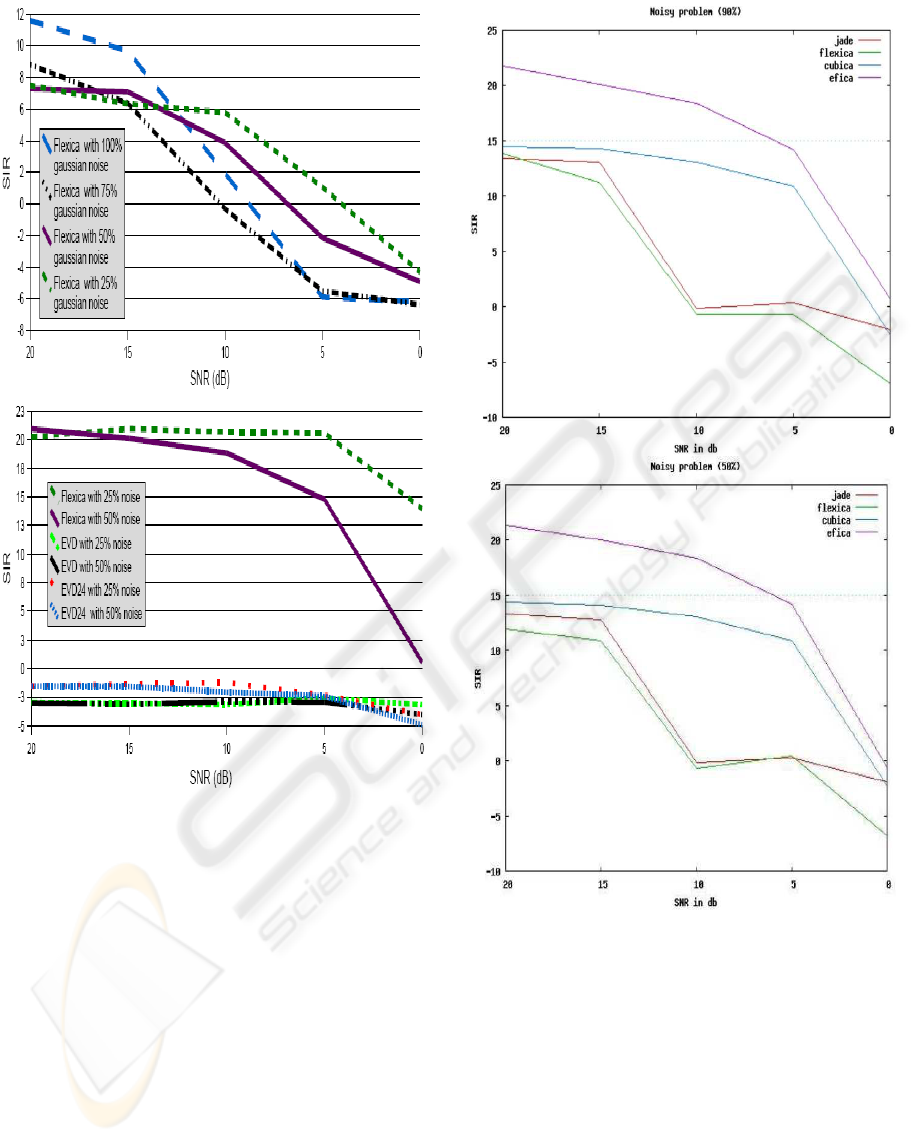
Figure 6: Upper part: SIR global performance index for the

noisy sub-problem 4 (set 1) using synthetic data. Lower

part: SIR global performance index for the sub-problem 4

(set 2) using real world data with 25% and 50% uniform

noise.

algorithms had serious problems coping with the in-

creasingly ill-conditioned mixing matrices and were

unable to converge, i.e. to complete computation in

cases where the matrix was unfortunately too close

to singular. This problem turned out to be dependent

on the dimension of the mixing matrices. Therefore

for these two algorithms, the only SIR values that

could be estimated are for dimensions 2 to 16.

Surprisingly, EfICAs performance drops signiﬁcantly

between dimensions of 8 and 16 to a level below

that of the other algorithms. One might predict

that, on the contrary to the sub-problems examined

before, EfICAs performance will remain inferior to

the other algorithms with increasing dimensionality.

Furthermore when looking at the graphs in the lower

Figure 7: Upper part: SIR global performance index for

sub-problem 4. Lower part: Sub-problem 4 with 50% noise.

part of ﬁgure 5 showing FlexICAs performance up

to a dimension of 16 - FlexICA might turn out to

perform best among the four algorithms examined for

dimensions higher than 16 in the case of increasingly

ill-conditioned mixing matrices.

Noisy problem

The fourth and ﬁnal sub-problem adds successively

increasing noise levels in the mixing process. This has

been achieved by using the noise progression module

provided by the test engine. This simpliﬁed testing

AN ALGORITHM EVALUATION TEST SUITE FOR BLIND SOURCE SEPARATION PROBLEM

191

the algorithms. For this sub-problem, only the per-

formance of the FlexICA algorithm was of interest

as the EVD methods did not manage to separate the

mixtures. Even FlexICA’s performance was not re-

markable, not reaching the required SIR of 15dB with

synthetic data at any noise level.

With speech data, FlexICA’s performance is some-

what better as can be seen in the lower part of ﬁg-

ure 6. It remains satisfactory up to a SNR level of

5dB with 50% noise. This could be attributed to the

super-Gaussian nature of the speech signals. As wit-

nessed in all other sub-problems as well, both EVD

algorithms are unﬁt to address the tasks given. This

time even FlexICA’s performance on datasets with

Gaussian noise was not remarkable, not reaching the

required SIR of 15dB with synthetic data at any noise

level (see upper part of ﬁgure 6).

Starting out with 20dB, the SNR was gradually re-

duced by 5dB until it reached 0dB for the second

competition of algorithms (see ﬁgure 7 for reported

results). FlexICA’s performance on datasets with

Gaussian noise was not remarkable and did not reach

the required SIR of 15dB with synthetic data at any

noise level. On the other hand, for this speciﬁc sub-

problem, CubICA shows to perform best among those

algorithms that did not reach the required SIR>15dB

margin at any noise level. Finally, it is the EfICA

algorithm again that outperforms the others on aver-

age, showing its typical behaviour with respect to an

increasing SNR level. In comparison to the results

for 50% (upper part ﬁgure 7) and 10% noise (lower

part of ﬁgure 7), EfICA and CubICA performs ex-

actly equal.

4 CONCLUSION

We have shown that the testsuite allows for the sys-

tematic and automated evaluation of blind source sep-

aration algorithms and supports the development of

new algorithms by providing an easy way of standard-

ized comparison. For the given test problems we have

determined an optimal combination of pre-processing

steps and corresponding optimal parameters for se-

lected known algorithms. The systematic search for

optimal parameters may allow using the full potential

of existing and new algorithms. Concerning the algo-

rithms of the second group (FlexICA, CubICA, JADE

and EfICA) it remains to say, that they perform quite

well. Especially at higher dimensions and at higher

noise rates newer algorithms are able to outperform

FlexICA. The results strongly imply the use of spe-

ciﬁc algorithms for different application context. A

context dependent adaptive expert toolbox for differ-

ent application scenarios would maximize the BSS-

application performance.

REFERENCES

Cichocki, A. and Amari, S.-I. 2002. Adaptive Blind Signal

and Image Processing, (Wiley).

Hyv

arinen, A., Karhunen, J. and Oja E. 2001. Independent

Component Analysis, (Wiley).

Giannakopoulos, X. 1998. Comparison of Adaptive Inde-

pendent Component Analysis Algorithms, (Helsinki

University: Master Thesis).

Calhoun, V., Adali, T., Larsen, J., Miller, D. and Douglas,

S. 2005. Proceedings of IEEE Machine Learning for

Signal Processing Workshop XV.

Cardoso, J.-F. 1999. High-Order Contrasts for Independent

Component Analysis, Neural Computation, 11(1):

157–192.

Blaschke, T. and Wiskott, L. 2003. CubICA: Indepen-

dent Component Analysis by Simultaneous Third-

and Forth-Order Cumulant Diagonalization, Com-

puter Science Preprint Server (CSPS): Computational

Intelligence/0304002.

Koldovsky, Z. and Tichavsky, P. 2005. Efﬁcient Vari-

ant of Algorithm FASTICA for Independent Compo-

nent Analysis Attaining the CRAMER-RAO LOWER

BOUND, IEEE Statistical Signal Processing Work-

shop, Bordeaux..

Borschbach, M. and Schulte, M. 1999. Performance Analy-

sis of Learning Rules for the Blind Separation of Mag-

netencephalography Signals, Proc. of ICA’99, First

Int. Workshop on Independent Component Analysis

and Signal Separation, pp. 341–346.

Hagen, C. 1997. Neural Networks and Multivariate Statisti-

cal Data Analysis (in German), (University of Darm-

stadt: Ph.D. Thesis.)

Testengine and -suite. 2006. http://cs.uni-muenster.de/ICA/

;-last date of access 03.05.2006.

Schobben, D., Torkkola, K., and Smaragdis, P. 1999. Eval-

uation Blind Signal Separation Methods”, Proc. of

ICA’99, First Int. Workshop on Independent Compo-

nent Analysis and Signal Separation, pp. 261–266.

Giannakopoulos, X., Karhunen, J. and Oja, E. 1999. An ex-

perimental comparison of neural algorithms for inde-

pendent component analysis and blind separation, Int.

J. of Neural Systems, Vol. 9, No. 2.

ICINCO 2006 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

192