
ELLIPTIC NET - A PATH PLANNING ALGORITHM FOR DYNAMIC
ENVIRONMENTS
Martin Saska
CTU in Prague, The Gerstner Laboratory for Intelligent Decision Making
Technicka 2, 16627 Prague 6, Czech Republic
Informatics VII: Robotics and Telematics, University Wuerzburg, Germany
Miroslav Kulich and Libor P
ˇ
reu
ˇ
cil
CTU in Prague, Center of Applied Cybernetics and The Gerstner Laboratory for Intelligent Decision Making
Technicka 2, 16627 Prague 6, Czech Republic
Keywords:
Path planning, Graph searching, Robotic soccer, Obstacle avoidance, Mobile robot, Ellipse.
Abstract:
Robot path planning and obstacle avoidance problems play an important role in mobile robotics. The standard
algorithms assume that a working environment is static or changing slowly. Moreover, computation time and
time needed for realization of the planned path is usually not crucial. The paper describes a novel algorithm
that is focused especially to deal with these two issues: the presented algorithm - Elliptic Net is fast and
robust and therefore usable in highly dynamic environments. The main idea of the algorithm is to cover an
interesting part of the working environment by a set of nodes and to construct a graph where the nodes are
connected by edges. Weights of the edges are then determined according to their lengths and distance to
obstacles. This allows to choose whether a generated path will be safe (far from obstacles), short, or weigh
these two criterions. The Elliptic Net approach was implemented, experimentally verified, and compared with
standard path planning algorithms.
1 INTRODUCTION
Trajectory planning is one of the most important parts
of every robotic system. A new approach for mobile
robots working in a highly dynamic environment is
presented in this paper.
Standard obstacle avoidance approaches find a de-
sired path from an actual position S of the robot to
a desired goal position C, with respect to positions,
sizes, and shapes of known obstacles P in the envi-
ronment. The output of the algorithm can be either an
optimal trajectory connecting S with C (global algo-
rithms) or only direction from the actual position re-
specting locally optimal trajectory (local algorithms).
The basic requirement for the planned trajectory
is its optimality, which can be expressed as a length
of the trajectory or time needed to realize it. More-
over, the path should be easily feasible with respect
to both dynamic and kinematic constrains. In other
words, the path should be smooth path and does not
contain sharp turns. Unfortunately, ability to prevent
collisions is antagonistic to the requirement for path
optimality. Nevertheless, obstacle avoidance is nec-
essary, because collisions can cause damage of the
robot or obstacles and even endanger persons in ro-
bot’s workspace. To find an acceptable compromise
between these requirements (the length and the dis-
tance to obstacles) is one of the most crucial problems
in mobile robot planning.
Standard algorithms described in the literature
cover whole workspace of the robot by a squared or
hexagonal grid which causes that dynamic features of
a robot are not respected. Another problem of stan-
dard approaches is big computational time. Such al-
gorithms cannot be used in dynamic environments,
where re-planning is invoked with high frequency.
In this paper, a novel method (called Elliptic Net)
is presented that avoids drawbacks mentioned in the
previous paragraph. The key idea of the approach is
to represent the working environment by a structure
based on a set of ellipses. Generated paths are then
smoother and more feasible. Moreover, the presented
approach takes into account only an interesting part
of the workspace that leads to reduction of computa-
tional time.
The rest of the paper is organized as follows. A
short review of the most popular obstacle avoidance
techniques is presented in the section 2, while a novel
method called Elliptic Net reflecting special require-
ments of the mobile robotics is described in section 3.
Finally, experimental results are described in section
4 and conclusions are presented in section 5.
372
Saska M., Kulich M. and P
ˇ
reu
ˇ
cil L. (2006).
ELLIPTIC NET - A PATH PLANNING ALGORITHM FOR DYNAMIC ENVIRONMENTS.
In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 372-377
DOI: 10.5220/0001208403720377
Copyright
c
SciTePress
2 LITERATURE SURVEY
Comprehensive review of path planning and obstacle
avoidance methods can be found in (Latombe, 1991).
Algorithms usually used in mobile robotics are di-
vided there into two types: local and global. Local
approaches find only optimal direction from the ac-
tual position using information from a local area of
the robot. While locality of these approaches leads
to low computational time, generated trajectories are
not guaranteed to be globally optimal. Moreover, un-
availability of a full path can cause problems to low-
level regulators and strategy planning methods that
can need a full path for their better decision process.
Vector Field Histograms VFH (Borenstein and Ko-
ren, 1991), originally developed for obstacle avoid-
ance of robots equipped with sonars are a typical ex-
ample of local approaches. Similarly to a rotating
sonar exploring a space in 360 range, VFH obtains
histogram distances to the closest obstacle in each di-
rection. Directions whose distance is smaller than an
adaptive threshold are selected from this histogram.
Value of the threshold depends on a distance of the
robot to the goal position. The direction that has the
smallest angle to vector SC is chosen as optimal robot
heading. VFH cannot solve situations with high den-
sity of obstacles and with U-shape obstacles. Both
types of the workspace configurations caused move-
ments oscillation.
The most widely used collision avoidance method
is Potential Field (Khatib, 1986). It minimizes a
penalty function Z that consists of two parts. The re-
pulsive one describes influence of the obstacles in the
workspace, while the attractive part expresses inten-
tion to go to the desired point. In the other words, the
repulsive part discriminates paths that are close to ob-
stacles - it has a maximum in a centre of each obstacle
and decreases with a distance. The attractive part has
a global minimum in the goal of the robot and uni-
formly grows with a distance to the goal. The biggest
problem of this approach is that optimisation can fin-
ish in a local minimum and therefore a globally opti-
mal path is not guaranteed to be found. The Potential
Field algorithm is used in this paper for comparison
with the following penalty function:
Z(x, y) =
(x − G
x
)
2
+ (y − G
y
)
2
+
+c
1
(
1
x − A
x
−
1
x − B
x
+
1
y − A
y
+
1
y − B
y
) +
+c
2
N
j=1
(exp(−c
3
((x − P
jx
)
2
+ (y − P
jy
)
2
))). (1)
G is the desired position of the robot, [P
jx
, P
jx
] are
coordinates of a center of j−th obstacle, A is a left
bottom corner of the playground (we suppose that the
workspace has a rectangular shape with boards along
it), B is a right top corner of the playground and c
i
are
constants weighting influences of the attractive and
repulsive parts.
Visibility Graph approach VG (Kunigahalli and
Russell, 1994) constructs a visibility graph (VG) of
vertices of polygons representing obstacles. It means
that two vertices are connected in VG if there are visi-
ble. A shortest path is then determined using standard
Dijkstra algorithm (Jorgen and Gutin, 1979). The
path found by this algorithm is typically close to the
obstacles, which often leads to collisions because ro-
bots cannot follow the planned path precisely. Grow-
ing of the obstacles by a certain value can solve this
problem, but it is not clear how to optimally determine
this value.
Occupancy Grid (Braunl and Tay, 2001) divides
a workspace into disjoint cells that cover the whole
space. The value of a cell is one if a part of any ob-
stacle is inside the cell or zero otherwise. Centres of
zero-valued cells are nodes of the graph, while edges
connect neighbouring nodes.
Voronoi Diagrams (VD) (Aurenhammer and Klein,
2000) divide a workspace into disjoint cells also.
Given a set P of points in the plane, one cell of VD is
a set of points that are closer to the specific point than
to any other point in P . For robotic purposes, the set
P contains centres of robots (excluding the one the
plan is generated for) plus points representing boards
around the playfield. One possibility is to represent
each barrier by a set of points placed along each bar-
rier, but it increases computation time. The second
way is to compute generalized VD where the set P
can contain lines also. As it the previously mentioned
algorithms, a shortest path in the graph where neigh-
bouring cells of VD are connected can be found by
Dijkstra algorithm.
VD find very safe paths, i.e. the paths are generated
as far as possible from obstacles. This is useful in
dense environments, while paths generated in sparse
spaces are needlessly long and cautious.
3 ELLIPTIC NET
In this section we introduce a novel obstacle avoid-
ance algorithm - Elliptic Net that is designed to have
a small computational complexity and to avoid disad-
vantages of above-described methods. The main idea
of the algorithm is to cover a whole working environ-
ment by a set of nodes and construct a graph, where
neighboring nodes are connected by an edge.
The algorithm consists of three main steps. In the
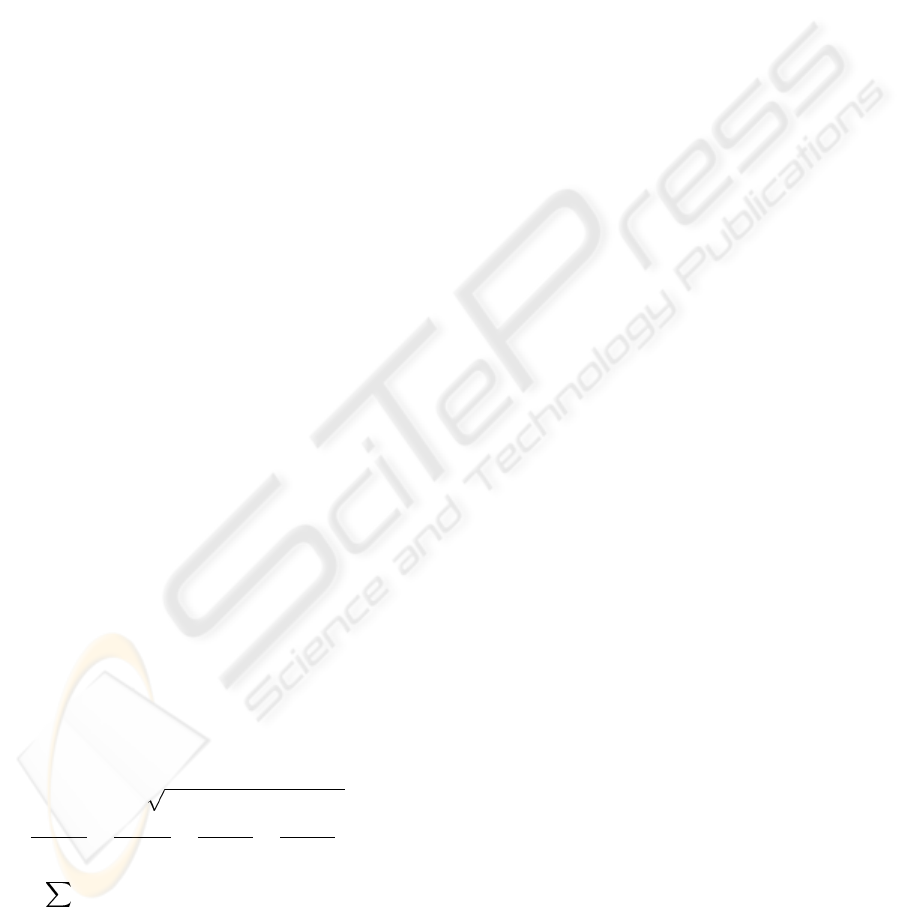
first one, topology of the net is created in a general
position (see Figure 1). A number of points in the net
depends on a distance between the start and the goal
position. In order to increase a speed of the algorithm,
ELLIPTIC NET - A PATH PLANNING ALGORITHM FOR DYNAMIC ENVIRONMENTS
373
the net is not computed on the fly. Instead of this,
several basic nets with a different number of points
are pre-computed. An appropriate net is then chosen
in a planning phase.
The net is then transformed (translated, rotated, and
resized) into a correct position according to the actual
and desired positions of the robot. Finally, weights
of edges in the graph are determined and the optimal
(according to the weights) path in the graph is found.
3.1 Net Description
Topology of the Elliptic Net is based on intersection
of a set of ellipses and a set of half-lines. i-th ellipse
is defined by its centre E(i) and lengths of its axes a(i)
and b(i) that are given by the following equations:
E
x
(i) = 0, (2)
E
y
(i) =
i + 1
2
−
(w −
1
2
)
2
2
.(i + 1).p, (3)
a(i) = p.b(i), (4)
b(i) =
i + 1
2
+
(w −
1
2
)
2
2
.(i + 1).p, (5)
i ∈ 1..
t − 1
2
,
where p is ratio of the lengths of axes, w is a num-
ber of nodes lying on the line SG and t is a number of
nodes that lie on axis y. The half-lines are determined
by the equation y = kx+q. Parameters k(j) and q(j)
of j-th half-line are determined by equations
k(j) = tg(
j
X
u=1
(
1
2
)
u
), (6)
q(j) = −k(j).(−(j + 1) +
w − 1
2
), (7)
i ∈ 1..
w − 1
2
,
Intersection points of all ellipses and lines define
nodes of the Eliptic Net in one quarter of the plane.
Rest of the nodes is obtained as an axial symmetry
according to the axes x and y as shown in Figure 1.
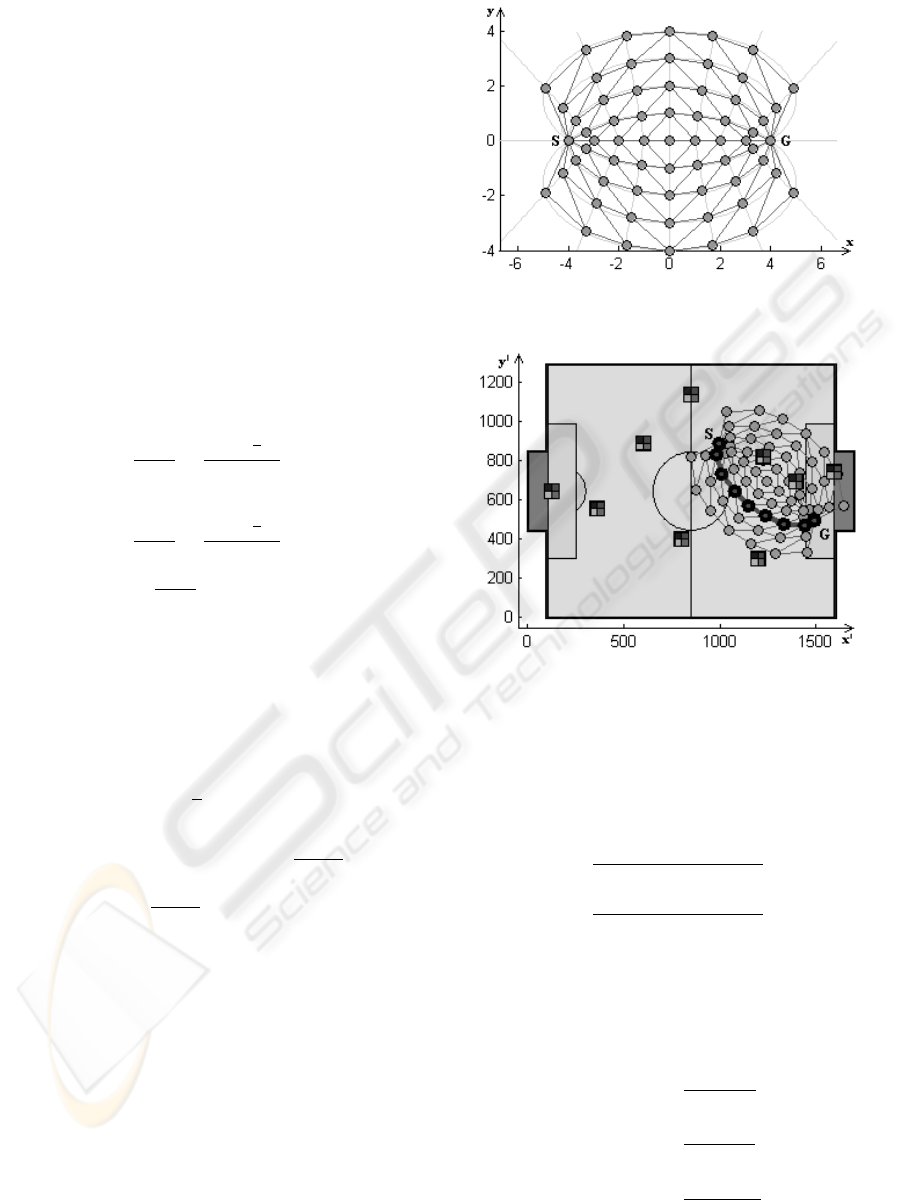
3.2 Transformed Net
In order to get optimal results, a distance between
neighbouring nodes should be comparable to the size
of obstacles. This requires generating a net with thou-
sands of edges to cover even a small area. Instead of
that only a grid of points covering the area along a
straight line connecting robot’s actual position with
the requested goal position is constructed.
Figure 1: Net in the basic form.
Figure 2: Net transformed to the correct position.
The net in a general position is transformed (ro-
tated, translated, and resized) to a correct position (see
Figure 2) according to the following equations:
x
′
=
x.cos(α) − y.sin(α)
k
+ S
x
, (8)
y
′
=
y.cos(α) − x.sin(α)
k
+ S
y
, (9)
where [x, y] are coordinates of a node in a pre-
defined net, [x
′
, y
′
] coordinates in the resulting net,
[Sx, Sy] robot’s start position, and k and α scale and
rotation parameters, which are calculated as follows:
cos(α) =
G
x
− S
x
d(S, G)
, (10)
sin(α) =
G
y
− S
y
d(S, G)
, (11)
k =
(n − 1).g
d(S, G)
, (12)
where n is a number of nodes, which lie on the line
ICINCO 2006 - ROBOTICS AND AUTOMATION
374

SG and g stands for a distance between two neigh-
bouring nodes on SG.
Weights of edges are finally evaluated according to
their lengths and positions of obstacles:
w(e) = length(e).(1 +
n
X
j=1
c
d(C(e), C(o
j
))
), (13)
where length(e) is a length of edge e, d(.) stands
for Euclidean distance, C(e) is the center of e, C(o
j
)
is the center of obstacle o
j
, n is a number of obstacles
and c is a constant. This means that the closer an edge
lies to some obstacle the higher is its weight. The op-
timal trajectory is then the cheapest path in this graph
found by Dijkstra algorithm.
4 EXPERIMENTAL RESULTS
The functionality and the robustness of the Elliptic
Net algorithm has been experimentally verified. The
goal of the first experiment was to set all constants in
an optimal way. The results of the experiment show
also influence of different settings of the parameters.
In the other part of testing, the Elliptic Net was com-
pared with two standard approaches often used in mo-
bile robotics. An experimental set of 1000 random
scenes was generated for both above-mentioned ex-
periments. Each scene contains 9 randomly generated
obstacles and random start and goal positions of the
robot. The set of scenes was a little bit reduced for
the second experiment ( see section 4.2).
The situations were solved by all algorithms and
the generated paths were evaluated and compared ac-
cording to several criteria (see Tables below). The
first criterion l stands for a length of the path; the other
one d describes ability of the algorithm to find a path
in safe distance from all obstacles. Precisely, it is the
shortest distance between any obstacle and the trajec-
tory. The values wc and hc mean a number of colli-
sions. The ”weak” collision wc occurs if d is smaller
than the robot radius. In this case the robot lightly
touches an obstacle and can push it. In the case d is
smaller than a half of the robot radius, we speak about
a ”hard” collision hc. The last, but one of the most
important criterion is t that describes computational
complexity. The complexity is described as a ratio of
time needed by the algorithm to time needed to solve
the same problem by Visibility Graph algorithm.
The third experiment consists in intensive testing
by simulations. The first simulator (Krajn
´
ık et al.,
2006) that we used was robotic soccer simulator.
It can simulate real robot moving through the pre-
planned trajectory and collisions with obstacles (other
robots and barriers). Figure 3 shows one of the situa-
tions in the robotic soccer and the trajectory that was
Figure 3: Situation solved by Elliptic Net.
Figure 4: Simulated path to the desired position.
founded by Elliptic Net. The real path that robot go
through is visualized in the figure 4. Other simulation
contains of a trajectory generator that approximate the
founded trajectory by a spline curve that respects the
robot motions constraints. This approach is closely
described in (Saska et al., 2006) and some results for
all algorithms are shown in Figures 5,6.
4.1 Constants Setting
Influence of different settings of the constant c in
equation 13 on algorithm behavior that is evaluated
by indicators in Table 1 is described in this section.
Each row in the table shows values averaged for all
1000 situations from the experimental set.
Experiments show that the value of c can decide
whether the robot is controlled according safe (big c)
or fast (small c) strategy. In the first case, distance
ELLIPTIC NET - A PATH PLANNING ALGORITHM FOR DYNAMIC ENVIRONMENTS
375
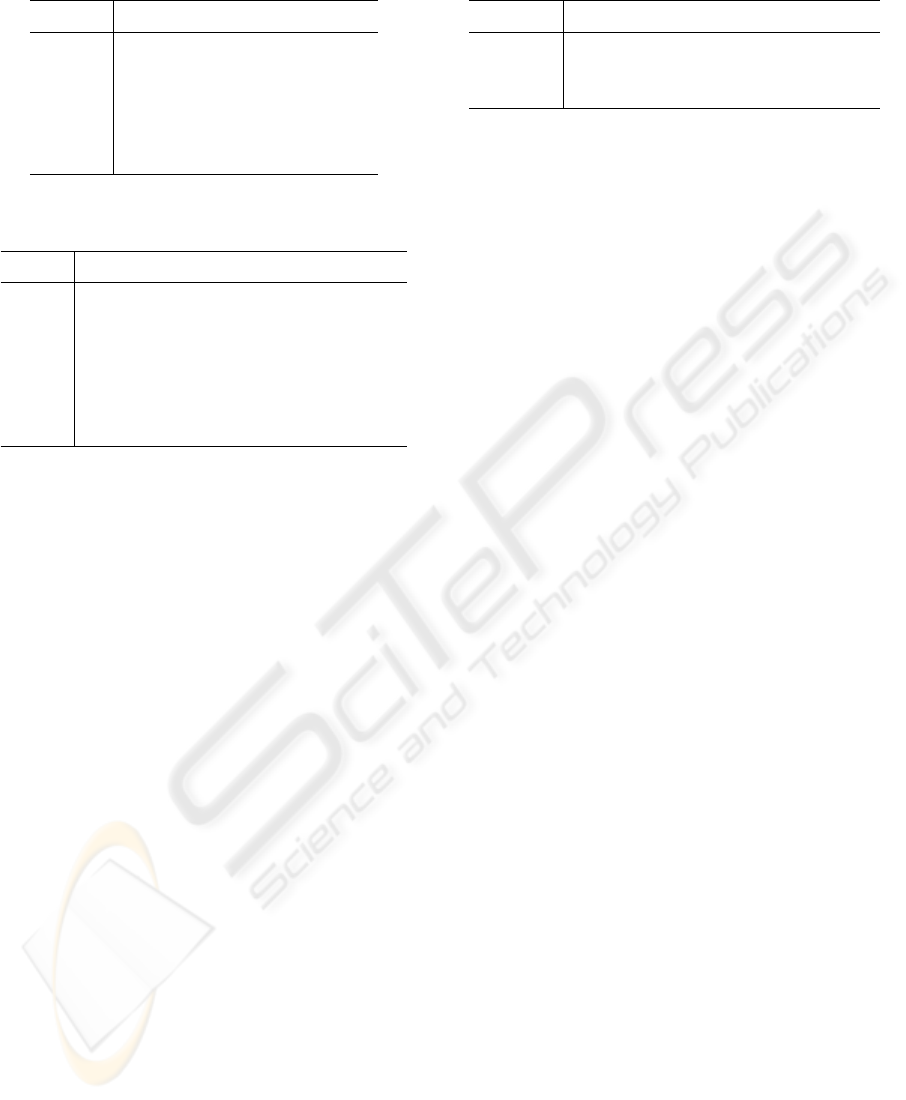
Table 1: Influence of constant c. Size of the net is 11x11.
c l[mm] d[mm] hc wc
500000 829.4 186.4 2 12
50000
819,2 183,9 1 10
25000
812,2 181,9 1 8
5000
742,6 156,6 9 102
2500
732,5 148,2 29 234
250
720,3 139,2 154 309
Table 2: Influence of size of the net. Constant c is 25000.
size l[mm] d[mm] hc w c t[%]
3x3 693,9 138,6 163 310 1,2
5x5
800,0 171,5 26 71 4,0
7x7
791,1 175,6 7 24 7,9
9x9
803,7 179,9 2 10 11,7
11x11
812,2 181,9 1 8 16,9
15x15
798,6 183,2 1 5 40,2
25x25
797,4 184,5 0 2 121,7
of a trajectory to obstacles increases and therefore the
number of collisions falls. It is caused by increas-
ing influence of obstacles, which ”pushes” a path to
the free space. A small value of c decreases distance
from the obstacles, but the trajectory is shorter and the
robot can reach the goal faster.
Relation among a size of the net, computational
time, and quality of the trajectory is evaluated in Ta-
ble 2. The rows depict different parameters according
to a number of nodes in the net. It can be stated that
nets with bigger than 7x7 produce remarkably smaller
number of paths with collisions. Interesting behav-
ior is shown in the second and third columns. These
two indicators are normally dependent in the sense
that a length of the path is increasing when a higher
safety is requested, which is not this case: with in-
creasing a net size, paths are shorter and more distant
from obstacles. This is caused by finer resolution of
larger nets that allow controlling generated paths with
higher precision. On the other hand, time complexity
is of course higher for bigger nets, so sizes 9x9 and
11x11 looks as a good compromise between quality
of generated paths and time complexity.
4.2 Algorithm Comparison with
Other Methods
The algorithm Elliptic Net is compared in this section
with two standard methods described above - Poten-
tial Field and Visibility Graph. The experiment con-
sists of two parts. The same set as in the previous
section was used in the first, but Potential Field ap-
Table 3: Different algorithms used for only 675 situations.
method l[mm] d[mm] wc nc t[%]
EN 741,5 205,2 0 7 28,4
PF
711,1 203,2 0 1 1,8
VG
667,0 175,1 0 134 100
proach was successful only in 675 situations, because
its optimization process can gets stuck in a local min-
imum. We therefore reduced the set to 675 situations
where the Potential Field gets results, otherwise the
results evaluated in Table 3 would be biased.
Visibility Graph has shortest average lengths (see
second column in the table), which corresponds with
expectations. Results obtained by the other ap-
proaches are nevertheless similar - they differ only by
4%. On the other hand, the trajectories found by the
Visibility Graph are too close to the obstacles, which
causes frequent crashes.
All situations used for the statistics in Table 3 were
solved without even weak collisions as shown in the
third column. That’s why we don’t use a number of
hard collisions as the other indicator, but a number of
trajectories nc that have a distance to the nearest ob-
stacle smaller than a robot radius multiplied by two.
20% of paths generated by the Visibility Graph algo-
rithm were dangerously near to obstacles, while other
two methods give significantly better results.
The last indicator in the sixth columns is computa-
tional time. The Potential Field is fastest according to
this criterion, but the value in the table describes time
needed to find only optimal robot’s heading instead
of the whole trajectory. If we use full version of the
algorithm generating whole trajectory, computational
time increases dramatically and it is then longer than
time needed by the Visibility Graph. The Elliptic Net
with 13x13 nodes is 3.5 times faster than the Visibility
Graph.
In the second part of the comparative experiments,
all algorithms were verified and their behaviour com-
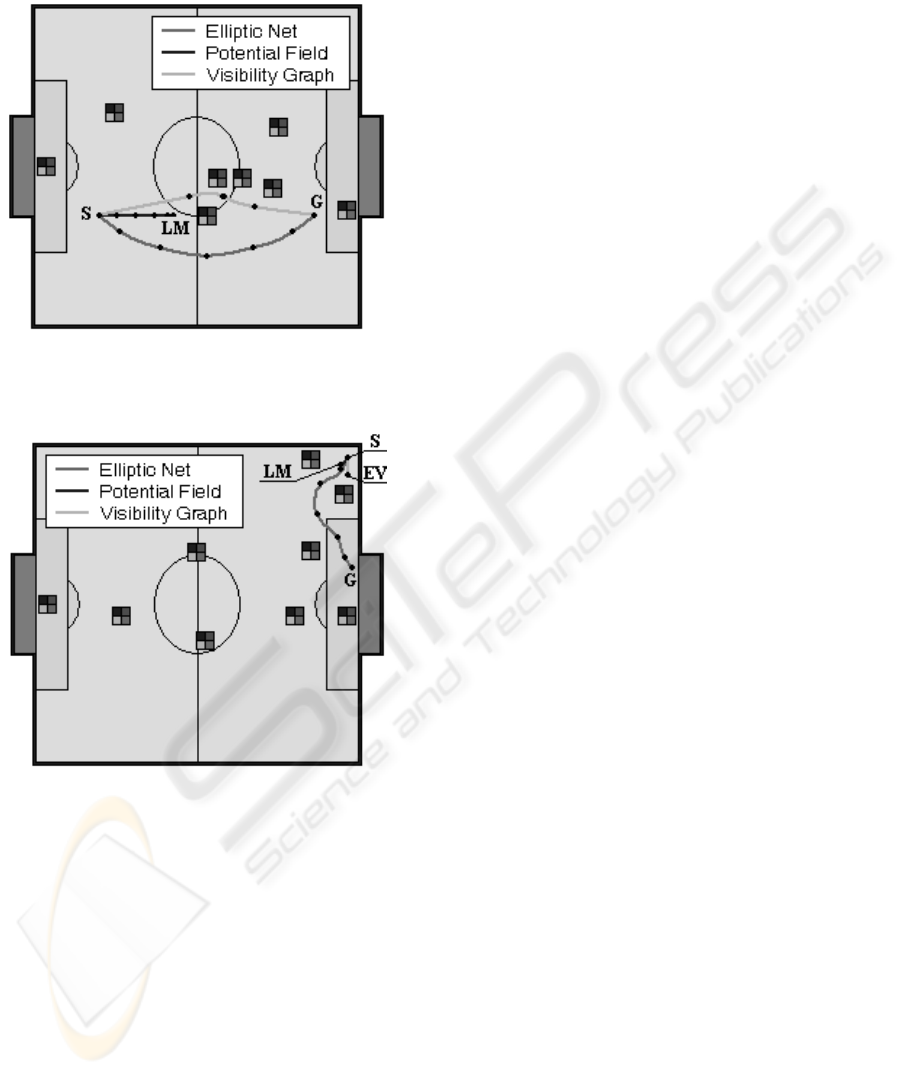
pared on two types of simulations. Figure 5 shows
the ability of the Elliptic Net to avoid a cluster of the
obstacles. On the contrary, A trajectory found by the
Visibility Graph goes through this cluster. The path is
also too close to the obstacles, which can lead to col-
lision in case of odometry or control error or sudden
moving of the obstacle. Other important advantage
of the Elliptic Net is illustrated in Figure 6. This ap-
proach finds an optimal solution if a free path without
collision does not exist. The Visibility Graph is dis-
connected in such case and an optimal trajectory is
not found. The Potential Field gets stuck in the local
minimum in the same way as in the previous situation.
Paths generated by the algorithms were smoothed
by the spline generator and final trajectories executed
ICINCO 2006 - ROBOTICS AND AUTOMATION
376
by the robot in the simulator were drown in both situ-
ations.
Figure 5: Situation solved by different algorithms.
Figure 6: Situation solved by different algorithms.
5 CONCLUSION
The Elliptic Net described in this paper is a novel
path planning algorithm that can be used in simple,
but dynamic environments. The optimal path is found
on a graph, whose nodes are determined as intersec-
tion of a specially created set of ellipses with a set of
half-lines. Most of the final trajectories are smooth,
i.e. without sharp curves and a robot can follow the
planned path quickly.
This approach needs less computational time than
the other global algorithms and therefore it is accept-
able in highly dynamic environments where frequent
re-planning is needed. Local algorithms are of course
faster, but they have problems with clusters of the ob-
stacles and with local extremas. Quickly moving ob-
stacles are the reason, why the algorithm tries to avoid
them with sufficient distance. Other important advan-
tage is its robustness. Algorithm has the ability to find
some trajectory if a free path without collision doesn’t
exist. Like in a real life, it holds that bad decision is
better than no decision.
In the future, we would like to incorporate dynamic
obstacles directly into the algorithm. The idea is to
predict positions of obstacles (other robots) accord-
ing to their current states and situation on the field
and evaluate edges in the planning graph according to
these predictions.
ACKNOWLEDGEMENTS
The work has been supported within the Czech-
Slovenian intergovernmental S&T Cooperation Pro-
gramme under project no. 10200506 ”Cooperative
mobile robots for industry and service”. The support
of the Ministry of Education of the Czech Republic,
under the Project No. 1M0567 to Miroslav Kulich is
also gratefully acknowledged.
REFERENCES
Aurenhammer, F. and Klein, R. (2000). Voronoi diagrams..
pages 201–290.
Borenstein, J. and Koren, Y. (1991). The vector field his-
togram: Fast obstacle avoidance for mobile robots.
IEEE Journal of Robotics and Automation.
Braunl, T. and Tay, N. (2001). Combining configura-
tion space and occupancy grid for robot navigation.
28(3):233–41.
Jorgen, B. and Gutin, G. (1979). Digraphs: Theory, Algo-
rithms and Applications. Elsevier North Holland.
Khatib, O. (1986). Real-time obstacle avoidance for manip-
ulators and mobile robots. The International Journal
of Robotics Research, 5:90–98.
Krajn
´
ık, T., Faigl, J., and P
ˇ
reu
ˇ
cil, L. (2006). Decision sup-
port by simulation in a robotic soccer domain. In
MATHMOD 2006, ARGESIM-Reports.
Kunigahalli, R. and Russell, J. (1994). Visibility graph ap-
proach to detailed path planning in cnc concrete place-
ment.
Latombe, J. (1991). Robot Motion Planning. MA: Kluwer,
Norwell.
Saska, M., Kulich, M., Klancar, G., and Faigl, J. (2006).
Transformed net - collision avoidance algorithm for
robotic soccer. In MATHMOD 2006.
ELLIPTIC NET - A PATH PLANNING ALGORITHM FOR DYNAMIC ENVIRONMENTS
377
