
LOCALIZATION WITH DYNAMIC MOTION MODELS
Determining Motion Model Parameters Dynamically in Monte Carlo Localization
Adam Milstein
Department of Computer Science, University of Waterloo, Waterloo, Ontario, Canada
Tao Wang
Department of Computing Science, University of Alberta, Edmonton, Alberta, Canada
Keywords: Mobile Robots, Localization, Machine Learning.
Abstract: Localization is the problem of determining a robot’s location in an environment. Monte Carlo Localization
(MCL) is a method of solving this problem by using a partially observable Markov decision process to find
the robot’s state based on its sensor readings, given a static map of the environment. MCL requires a model
of each sensor in order to work properly. One of the most important sensors involved is the estimation of
the robot’s motion, based on its encoders that report what motion the robot has performed. Since these
encoders are inaccurate, MCL involves using other sensors to correct the robot’s location. Usually, a
motion model is created that predicts the robot’s actual motion, given a reported motion. The parameters of
this model must be determined manually using exhaustive tests. Although an accurate motion model can be
determined in advance, a single model cannot optimally represent a robot’s motion in all cases. With a
terrestrial robot the ground surface, slope, motor wear, and possibly tire inflation level will all alter the
characteristics of the motion model. Thus, it is necessary to have a generalized model with enough error to
compensate for all possible situations. However, if the localization algorithm is working properly, the result
is a series of predicted motions, together with the corrections determined by the algorithm that alter the
motions to the correct location. In this case, we demonstrate a technique to process these motions and
corrections and dynamically determine revised motion parameters that more accurately reflect the robot’s
motion. We also link these parameters to different locations so that area dependent conditions, such as
surface changes, can be taken into account. These parameters might even be used to identify surface
changes by examining the various parameters. By using the fact that MCL is working, we have improved
the algorithm to adapt to changing conditions so as to handle even more complex situations.
1 INTRODUCTION
Localization is the problem of determining a robot’s
accurate location in an environment based on
inaccurate sensor information. For most complex
tasks, a robot must know its current location before
it can perform any useful actions. In fact, a robot
needs to know its current location in order to find a
specific subsequent location where it needs to
perform an action. Effective localization is
fundamental to most mobile robot applications. The
problem of localization arises from the fact that all
physical sensors are inaccurate. If the encoders on a
robot gave the exact distance moved without error,
then there would be no localization problem. After
any motion, the robot would be at the location given
by the encoders. Unfortunately, no physical sensors
are perfect. Robots commonly have some type of
range sensor which is used together with a map of
the environment to determine the actual motion. Of
course, range sensors are also prone to error.
Localization is the problem of compensating for all
of these errors and producing an accurate position.
One common algorithm for localization is Monte
Carlo Localization (MCL) (Thrun et al 2005). MCL
combines various sensor models and a map of the
environment, using a recursive Bayes filter to
estimate the belief state of the robot’s location.
Obviously, the quality of these models is important.
Although MCL is robust to some errors in the
120
Milstein A. and Wang T. (2006).
LOCALIZATION WITH DYNAMIC MOTION MODELS - Determining Motion Model Parameters Dynamically in Monte Carlo Localization.
In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 120-127
DOI: 10.5220/0001204501200127
Copyright
c
SciTePress

models and map, the combination of different errors
can cause it to fail.
Since most of the time MCL works properly,
finding the correct localization for the robot, it is
possible to correct various errors in the models to
allow MCL to converge to a correct solution even
more accurately. Although improvements are
unnecessary when the algorithm is already working,
by making corrections the errors should not build up,
and future situations may be easier to solve
correctly. Since minor errors in MCL can combine
to produce problems, reducing minor errors when
they have no impact prevents those same errors from
building up with other errors to cause localization
failures.
One situation where reducing minor errors is
critical is in the case of global localization. This is a
special case of localization where the robot’s starting
position is unknown. In this case, the entire space
must be searched and minor errors can easily cause
global localization to fail. If some of these minor
errors can be removed during ordinary execution,
then global localization in the future may be easier.
It has already been demonstrated that the static
map of the environment required by MCL can be
updated during ordinary execution to accommodate
changes in the environment (Milstein, 2005). In this
article, we demonstrate that it is also possible to
update the parameters of the motion model during
execution of MCL to provide a more accurate idea
of how the robot moves through the environment. In
general, a single, simplified, motion model is created
that reflects some idea about how a robot moves.
This model is necessarily a generalization because
the robot’s motion is effected by various changing
situations, such as the surface it moves on, and
possibly the power of the batteries or the inflation
and wear on the tires. While all of these situations
could be monitored and manually compensated for,
it would require an enormous amount of work to
create a motion model that reflected all of these
different states. It is also impossible to predict all
possible circumstances, so such a complex model
would be invalidated by any unanticipated change in
conditions. By automatically updating the motion
model according to the observations, it is possible to
optimize the model to any situation, even if that
situation has not been predicted in advance. As the
model is updated, errors in MCL due to the motion
model are reduced, leaving greater tolerance for
errors caused by other factors.
2 BACKGROUND
Monte Carlo Localization uses models of various
sensors, together with a recursive Bayes filter, to
generate the belief state of a robot. In fact, MCL is a
specific instance of a POMDP. A standard form of
MCL uses a motion model to predict the robot’s
motion together with a sensor model to evaluate the
probability of a sensor reading in a particular
location. The sensor model necessarily includes a
static map of the environment. The algorithm can be
applied to virtually any robot with any sensor
system, as long as these two models can be created.
One common implementation where MCL is very
successful is on a wheeled robot using a range
sensor such as a laser rangefinder. One benefit of
this combination is that the map and location used
by the algorithm are in a human readable format.
Although we give the general algorithm in the
following sections, which should be applicable to
other robots, where application specific details are
required, we assume the type of robot as described.
2.1 Recursive Bayes Filter
MCL is an implementation of a recursive Bayes
filter. The posterior distribution of robot poses as
conditioned by the sensor data is estimated as the
robot’s belief state. A key detail of the algorithm is
the Markovian assumption that the past and future
are conditionally independent given the present. For
a robot this means that if its current location is
known, the future locations do not depend on where
the robot has been. In virtually any environment this
is the case, so making the assumption is reasonable
in general.
To produce a recursive Bayes filter, we
represent the belief state of the robot as the
probability of the robot’s location conditioned by the
sensor data, where sensors include odometry.
(1)
x
t
represents the robot’s position at time t, z
t
the
robot’s sensor readings at time t and u
t
is the motion
data at time t. To simplify the subsequent equations
we use the notation that a
t
= a
t
, …, a
0
.
While this equation is a good representation of
the problem, it is not much use since it can not be
calculated as is. By applying a series of
probabilistic rules, together with the Markovian
assumption, equation 1 is factored into:
(2)
Obviously, p(x
t-1
| z
t-1
, u
t-1
) is Bel(x
t-1
) giving us
the recursive equation necessary for a recursive
),...,,,...,,|()(
0101
uuuzzzxpxBel
tttttt −−
=
∫
−
−−
−−
=
1
),|(),|()|()(
11
11
t
x
tt
ttttttt
uzxpuxxpxzpxBel
η
LOCALIZATION WITH DYNAMIC MOTION MODELS - Determining Motion Model Parameters Dynamically in
Monte Carlo Localization
121

Bayes filter. η is a normalization constant that can
be calculated by normalizing over the state space.
p(z
t
| x
t
) is the sensor model, representing the
probability of receiving a particular sensor reading
given a robot’s location. Finally, p(x
t
| x
t-1
, u
t
) is the
motion model. It is the probability that the robot
arrives at location x
t
given that it started at location
x
t-1
and performed action u
t
. The sensor and motion
model are representations of the physical
components of the robot and must be determined
experimentally for each robot and sensor device.
2.2 Particle Approximation
It would appear that, given the two models, equation
2 is all that is necessary to perform localization with
MCL. Unfortunately, a problem occurs with the
integral. The equation requires integrating over the
entire state space. Although we can evaluate the
models at any point in the space, there is no closed
form to the integral. Further, the simplest kind of
robot moves in a continuous, 3 dimensional state
space with an x and y location together with an
angle of rotation. Calculating the integral over this
space is impossible, especially for a real time
algorithm. In order to solve this problem, we
approximate the continuous space with a finite
number of samples. The integral over the space
becomes a sum over the finite number of particles.
Of course, approximating the space results in a
certain amount of error when low probability
locations are not represented. If the robot is really at
one of these locations it can never be localized.
However, if the number of particles is well chosen
MCL works well in most situations.
2.3 Algorithm
As the robot moves, it reports its odometry and
sensor data to the MCL algorithm. After each move
each particle is moved randomly according to the
motion model, based on the motion actually
reported. The particles are then updated with a
weight determined by the sensor model for the
particle’s location. Finally, the particles are
resampled by repeatedly choosing samples
randomly, with replacement, from the current set,
according to the weights assigned by the sensor
model.
The effect of resampling is to replace the
weight of the individual particles with the number of
particles at that location. On the robot’s next move
the particles at a high probability location will
spread out as they are moved randomly according to
the motion model, with at least one landing in the
robot’s new location. Then the resampling will
cause more particles to appear at the correct
location, while incorrect locations die out.
Assuming that the models and map are accurate,
MCL will correctly track the robot’s changing
location. Various parameters can be tuned manually
to adjust the rate of convergence and the behaviour
of the models. Once the belief over the robot’s
location is generated, a single location for the robot
can be found by looking at the mean of the particles.
2.4 Motion Model
The motion model p(x
t
| x
t-1
, u
t
) is a critical part of
MCL. Unlike the sensor model, which gives the
probability of getting a specific sensor reading at a
particular location, it is necessary to sample from the
motion model. Given a starting location and a
reported motion (x
t-1
and u
t
), MCL requires that we
be able to choose a final location randomly
according to the motion model. This requirement
precludes us from using any motion model that is
very complex. In fact, most motion models are a
combination of simple Gaussian distributions. For a
holonomic wheeled robot the most common
representation is with two kinds of motion leading to
three kinds of error. Each movement of the robot is
represented as a linear movement followed by a
stationary turn. Although a particular robot
probably does not follow these exact motions, if we
break the robot’s motion into small increments we
can use them as an approximation.
Each translation of the robot is approximated by a
Gaussian where the mean is the reported distance
and the variance is the reported distance multiplied
by a parameter. This representation reflects the fact
that the range error increases the further the robot
travels. Rotation is also represented by a Gaussian.
The mean is again the reported angle, but the
variance is a parameter multiplied by the angle
turned, added to another parameter times the
distance moved. The variance takes into account
both turn error, which increases as the robot turns,
and drift error. Drift error is defined as the robot
turning when it tries to go straight. Obviously, it
increases the further the robot has travelled.
Although it would seem that drift error should be
minor, if it occurs at all, this is not in fact the case.
Many holonomic wheeled robots use a system where
the difference in motion between the drive wheels is
used to turn the robot. In such robots, moving
forward is accomplished by turning both wheels the
same amount, while turning is done by moving the
wheels different amounts. It is very likely that,
while moving forward, the wheels turn at slightly
different rates, causing the robot to rotate. The three
parameters involved in the model are often given as
ICINCO 2006 - ROBOTICS AND AUTOMATION
122

k
r
for range error, k
θ
for turn error, and k
d
for drift
error.
These two Normal distributions together
represent the motion model for many common
robots. However, the algorithms described in this
paper should work for any model, provided it is
possible to sample from it. In general, some
collection of Gaussians works well, since they are
often good approximations to a physical system
while at the same time being easy to sample from
and optimize.
3 DYNAMIC MOTION
The MCL algorithm depends on certain static
parameters that must be manually tuned for each
implementation. In particular, the sensor model
relies on a static map of the environment, while the
motion model requires parameters that reflect the
specific robot’s motion in the particular
environment. Since most interesting problems occur
in dynamic environments, or environments with
different conditions in different areas, these static
parameters are only a broad approximation.
Fortunately, MCL is robust to errors in the map and
motion model and will successfully localize a robot
as long as these parameters are a reasonable
representation. However, the more error there is in
the static parameters, the less tolerance the algorithm
has for errors from other sources. For example, if
the environment changes so that the map becomes
less accurate, perhaps because of furniture being
moved, then an error in the motion model might put
the robot in the wrong location. If the changes in the
map make an incorrect location look correct to
MCL, then there is far less tolerance for the motion
model to predict incorrect locations. Either of these
errors might be recoverable on their own, but both
together could cause a localization failure. If the
motion model is correct, then the robot’s next
location will be predicted correctly, and the fact that
there is a similar location somewhere else won’t
matter. Similarly, if the map is accurate, then an
incorrect prediction from the motion model will be
low probability and will die out in favour of the
correct location. As errors in any static parameter
build up over time, MCL’s tolerance towards
additional errors is reduced until it becomes
necessary to manually correct the parameters.
We already know that if MCL is successfully
localizing the robot it is possible to automatically
correct the map of the environment (Milstein, 2005).
When the robot’s location is known, any differences
between its sensor readings and the map are
probably caused by errors in the map, rather than
errors in the sensors. This is especially true if the
readings are repeated over time. It is possible to use
sensor readings taken when the robot is localized to
correct the map. With this modification the static
map becomes more accurate over time, instead of
less accurate. Of course, it requires several
observations to update the map, since a real
environment might have transitory objects which
should not be in the map, such as people. Thus,
even with a dynamic map, there are still errors that
will reduce MCL’s tolerance to other problems.
3.1 Motion Model Error
On each step of execution, MCL uses the motion
model to predict a new location for the robot, and
then uses the sensor model to correct that location.
Before the resampling step, the mean of the particles
represents the location determined by the motion
model. After resampling, the mean represents the
location of the robot according to the algorithm.
This means that a side effect of executing MCL is a
list of errors in the motion model. By recording
these values, we can dynamically generate a set of
errors that can be processed to correct the model.
Since each correction comes attached to a particular
location, we can even record in what part of the
environment the error occurred.
Given a set of errors, it would be quite easy to
determine the variance of a Gaussian distribution,
however, with the Gaussian motion model we are
using it is not quite so simple. The key realization is
that we are not trying to calculate the variance, we
are trying to find a parameter of the variance.
Remember that the motion model for a differential
drive robot depends on three parameters, range error,
turn error, and drift error, represented as (k
r
, k
θ
, k
d
).
If we let r be the distance travelled and θ be the
distance turned, while r
and θ are the estimations of
these values returned by the motion model, then the
distributions become:
(3)
which are both single valued Gaussians. From MCL
we are given a set of {r, θ, r
, θ} values and we wish
to optimise the models in the parameters {k
r
, k
θ
, k
d
}.
3.2 Variance Parameters
Because we wish to determine parameters to the
variance, instead of the variance itself, no standard
technique for estimating Normal distributions will
work. In fact, the problem is no longer a single
distribution, but rather a continuous set of
distributions for each value of (r
, θ). Fortunately,
the problem can be solved if we treat it as a general
),(),,( rkkNrkrNr
dr
•+•
=
•
=
θ
θ
θ
θ
LOCALIZATION WITH DYNAMIC MOTION MODELS - Determining Motion Model Parameters Dynamically in
Monte Carlo Localization
123

equation, instead of specifically as a probabilistic
distribution. The Gaussian equation for r becomes:
(4)
Since we want to have an
accurate model, we want the value of k
r
that
maximizes the probability. Given the set of data
produced by MCL, we would like to maximize the
probability obtained over that entire sample space.
(5)
Of course, (5) is a little unwieldy to calculate, but a
standard trick is to notice that if we maximize p(r)
we also maximize log(p(r)). Thus we are left with:
(6)
which is quite straightforward to maximize using
virtually any nonlinear technique. A similar process
for θ gives us a slightly more complicated equation
which is just as easy to solve.
(7)
Using an efficient nonlinear optimisation
algorithm, we can maximize these equations over
the parameters k
r
, k
θ
, k
d
for sets of data obtained by
MCL in real time. Although the functions are not
concave in these parameters, we have good starting
parameters available, since MCL is already using a
motion model. The current parameters make a good
starting point for the optimization. The new
parameters can be used immediately, while the data
is still collected to further refine them.
3.3 Algorithm
Now that we have a method to update the motion
model dynamically, we need to integrate it with
MCL, hopefully without significantly affecting the
runtime. One of the benefits of MCL is that it is a
fairly low cost algorithm and it is important that we
do not make changes that significantly increase the
amount of time it takes to run. Since MCL must run
in real time, whatever processing is necessary to
update the motion model must not delay
localization. With these requirements in mind, our
dynamic motion model MCL algorithm provides a
minor alteration that allows the parameters of the
motion model to be recalculated and used.
At each MCL update step a {r, θ, r
, θ} data point
is recorded. When enough new data points are
recorded to make it worthwhile to calculate new
parameters, the equation is maximized in the
background, using whatever power is available when
localization is finished. When the maximization is
complete, the new parameters are reported to the
MCL algorithm. In fact, MCL itself is unaware of
the changing parameters, since it just runs normally.
In order to reduce the complexity of the
calculation, only the most recent set of errors are
used. When a predetermined number of corrections
are recorded, each subsequent observation causes the
oldest observation to be removed. This creates an
upper bound for the maximization routine and also
allows the dynamic model to update to changing
conditions. For example, if the robot’s tires deflate,
or water is spilled on the floor, the motion of the
robot would change. In that case, after a certain
number of updates, all of the old data would be
removed and the model would be calculated entirely
based on the changed conditions.
In order to accommodate different conditions in
different areas, data points are not stored globally
but are instead recorded by region. Each region of
the map has its own collection of data. If there are
insufficient points to calculate the parameters then
the previous parameters are used. However, once
the robot traverses an area enough that it can update
the motion model, it calculates the parameters and
stores them with the area. When it subsequently
enters the same region, it can load the specific
parameters. Any reasonable algorithm for defining
regions can be used, smaller regions will be more
accurate but will take longer to receive enough data,
while larger regions will update sooner but may
represent multiple conditions.
The results of this dynamic motion model
algorithm are a map annotated with the motion
model parameters for different regions. Aside from
changing the motion model during execution, the
map can also be used to provide additional data for
planning or analysis. For example, if a region
causes a high variance, then it might be better for the
robot to avoid that region when path planning. Also,
a significant change in variance might indicate some
kind of spill that should be dealt with. A robot
might also use the different parameters to identify
different surfaces in the environment for another
machine, perhaps planning a route that avoids
certain kinds of surface.
Although creating dynamic motion models uses
successful localization to correct errors in the model,
it does not preclude using the same data to correct
other errors. In particular, it is possible to
))(2/()(
22
2
1
)(
rkrr
r
r
e
rk
rp
−−
=
π
∏
−− ))(2/()(
22
2
1
rkrr
r
r
e
rk
π
∑
−
−−
2
2
)(2
)(
)2log(
rk
rr
rk
r
r
π
∑
+
−
−
+−
2
2
)(2
)(
)2)log((
rkk
rkk
d
d
θ
θθ
πθ
θ
θ
ICINCO 2006 - ROBOTICS AND AUTOMATION
124
dynamically update the map of the environment as
in (Milstein, 2005), while simultaneously
dynamically updating the motion model. In fact,
using both of these together causes them both to
work better than either one alone. There is no
reason why other parameters could not also be
dynamically updated at the same time.
4 RESULTS
The dynamic motion model algorithm was tested
using a 2 wheeled Pioneer 3-DX differential drive
holonomic robot equipped with a 180 degree SICK
laser rangefinder. Data gathered by the robot over a
traversal of the environment was processed by both
the normal MCL algorithm and various
implementations of the dynamic motion model MCL
algorithm. The parameters of the motion model
were calculated by maximizing the equations as
described using Matlab’s ‘fminsearch’ function.
Dynamic map MCL (Milstein, 2005) was also used
to see if the two dynamic methods could be used
simultaneously. The results show a marked
improvement using dynamic motion models.
At first, standard MCL was used with some
default parameters for this class of robot. Although
these parameters work, they are general, high
variance parameters that have not been specifically
adapted to either the robot or the environment. With
these parameters the average error was 1.7% for
range and 4.5% for angle.
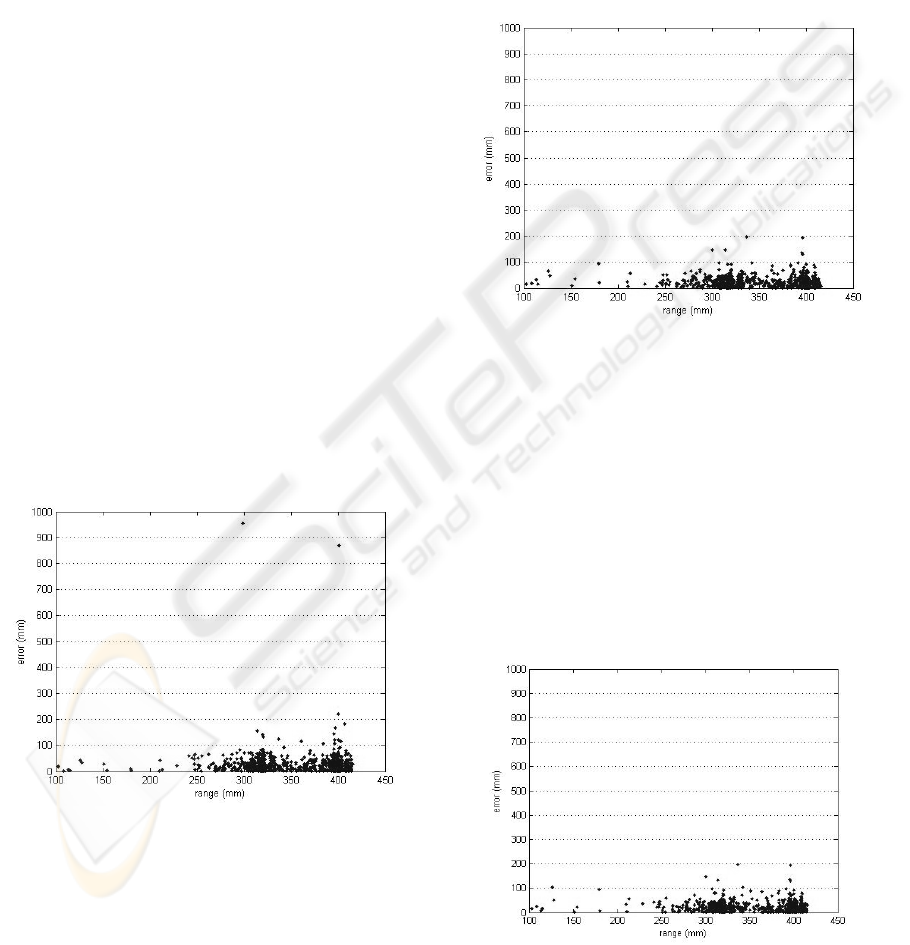
Figure 1: error vs. range for default parameters.
Figure 1 shows the error in range versus distance
moved for standard MCL. Because it is impossible
to separate the angle error caused by turning from
the angle error caused by range any graph of angle
error is not useful.
Next, the dynamic motion model algorithm was
used to calculate parameters based on the entire data
set and MCL was run with these motion model
parameters. The resulting error was 1.0% for range
and 2.9% for angle. Of course, in practice this
method is impossible, because it involves knowing
the observations that will be made before they are
actually recorded. In practice, this method can be
approximated by using a previous data set on the
same environment to calculate the parameters.
Figure 2 shows these motion parameters in action.
Figure 2: error vs. range for global optimization.
The third test involved dynamic motion models
with global data. The parameters were updated
during execution according to the preceding
localization corrections. With this method 1.2%
range error and 2.6% angle error was recorded.
Finally, the full dynamic motion model
algorithm was used. Each region of the map,
identified by the small circles, was updated with its
own data and produced its own corrections. This
technique produced an error of 1.4% for range and
2.8% for angle with characteristics as shown in
figure 3.
Figure 3: error vs. range for regional dynamic.
LOCALIZATION WITH DYNAMIC MOTION MODELS - Determining Motion Model Parameters Dynamically in
Monte Carlo Localization
125
As these results show, dynamic motion models are
better able to represent the robot’s motion, and
localization becomes more accurate. Table 1 shows
a comparison of the various methods. While all of
the dynamic methods give similar results, they are
far superior to the static motion model method that is
the base case. The particular method that is optimal
in any given situation depends on the environment,
although over the long run, the full dynamic
technique should produce the minimum error.
However, this convergence may require a large
number of traversals in order to get the necessary
number of data points for each region. Until
execution reaches this point, the other techniques
have a temporary advantage, since they require less
data.
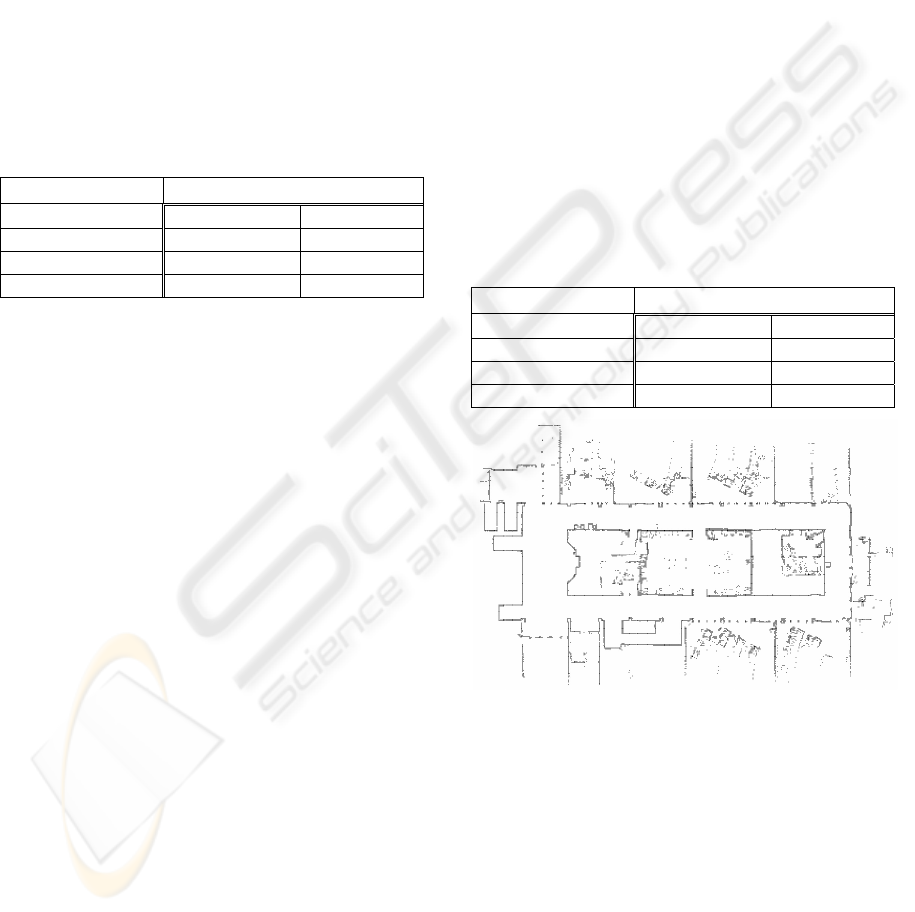
Table 1: Results of all algorithms.
% range error % angle error
Default static 1.6592% 4.5311%
Optimal static 1.0428% 2.9509%
Global dynamic 1.2418% 2.6320%
Regional dynamic 1.3882% 2.7878%
The technique of calculating the global
optimum parameters provides very good results,
especially in an environment like this with little
change in surface. Range error especially benefits
from this technique, since it is relatively constant.
However, generating this model requires manual
collection and processing of data before execution,
which somewhat defeats the purpose of a dynamic
algorithm. The benefit is that offline processing can
handle a larger number of data points, resulting in
more accurate parameters. Of course, any changes,
such as tire pressure, will invalidate the model.
Although this technique uses part of the dynamic
algorithm, it is not truly dynamic nor is it usually a
practical method.
The choice between the two dynamic
techniques depends on the circumstances. If the
environment has different surfaces then having the
parameters change with the region provides a
benefit. If, on the other hand, the surfaces are
constant but the robot changes conditions, a globally
dynamic technique will update more quickly, since
the data points are all processed into the same
model. A situation where this is useful might be
when the robot changes its behaviour as its battery
drains. The global technique could adapt faster to
changing robot conditions, but it cannot recognize
different surfaces. Note that the regional algorithm
will eventually adapt to global conditions, but it will
require more data since each region must be
updated. The choice depends strongly on the
environment, although the regional method is more
adaptable.
These results demonstrate that adding dynamic
motion models to MCL provides a benefit to
localization. Although slightly different dynamic
techniques provide different advantages, they are all
superior to the static technique. Aside from the tests
described above, several other data sets in different
environments were examined, with similar results.
One such test involved a similar robot in a different
building where the floor was carpeted instead of
concrete. The map of the environment incorporated
a serious error that caused localization to fail for
most techniques. One corridor was actually much
shorter than it appears in the map, causing motion
along part of that corridor to have a large bias.
Because of this, the range error in the dynamic
techniques actually increases, as they increase the
variance to handle the error. Only the regionally
dynamic technique was able to successfully localize
in this environment.
Table 2: Results of all algorithms for high error data.
% range error % angle error
Default static 7.2343% 5.9671%
Optimal static 8.6733% 1.3428%
Global dynamic 9.5313% 1.4835%
Regional dynamic 10.9178% 1.7166%
Figure 4: Environment used for the tests.
5 CONCLUSION
We have derived and implemented a technique for
dynamically calculating the parameters of the Monte
Carlo Localization motion model during ordinary
execution of the algorithm. Our technique requires
very little overhead and provides a strong benefit
over the ordinary technique of using a static model
determined experimentally from a similar robot. In
fact, the most common current technique is to
estimate the model and modify it using trial and
ICINCO 2006 - ROBOTICS AND AUTOMATION
126

error until localization is successful. The problem is
that performing experiments to determine the
parameters is a difficult and laborious process.
Since the parameters of a real environment change
over time, it is usually not worthwhile to develop an
accurate model when an approximate one will still
allow MCL to function. Our dynamic motion model
technique provides a viable alternative to both these
methods, allowing an accurate model to be created
and maintained without requiring skilled user input.
Since the frequency and size of the updates can be
modified to suit the platform, there is no reason not
to use a dynamic model. Because MCL is running
properly when the dynamic algorithm is active, there
is no urgency in processing the error data into new
parameters. Thus the additional run time required
can be limited to what is available on the particular
platform. Allocating more time will result in more
frequent updates, but since the alternative is no
updates there is no reason not to use even the
slowest possible rate. In fact, very good results can
be obtained by using offline processing to determine
a new model whenever conditions change.
Although the offline method does not provide all the
benefits of our full regional dynamic algorithm, it
provides a great improvement over the default
method.
Another benefit of having dynamic motion
models is that they can be used to automatically
optimize a robot to different conditions in the
environment. This may be an important feature for a
robot that runs autonomously between different
areas. It is impractical to perform laborious
experiments to determine an optimal model for
different regions, but a general model can be
automatically refined into specific models for many
different conditions.
By reducing the error due to the motion model
in MCL, our technique provides localization with
greater resilience to errors from other causes. The
more accurate the various models are, the more
tolerance MCL has towards random events that
might otherwise cause it to fail. In some
circumstances this may be a major benefit, but even
if ordinary MCL is successful in an environment, a
more accurate model cannot harm its execution.
Since dynamic motion model MCL provides an
annotated map which includes motion model
parameters, it may be possible to use those
parameters in order to determine information about
the environment. For example, by discovering the
parameters caused by various types of surface, the
robot might be able to identify those same surfaces if
it encountered them again. Also, the motion models
might be taken into account in path planning in order
to give the robot a preference for stable surfaces.
Finally, a robot might detect a change in its
parameters and use them to identify a malfunction,
such as deflated tires. These uses for dynamic
motion models would provide additional benefits to
the algorithm, above the improvements it makes to
localization.
REFERENCES
A. Milstein. 2005. Dynamic Maps in Monte Carlo
Localization. In 18
th
Canadian Conference on
Artificial Intelligence.
A. Milstein, J. Sanchez, and E.Williamson. 2002. Robust
global localization using clustered particle filtering. In
AAAI-02.
D. Avots, E. Lim, R. Thibaux, and S. Thrun. A
probabilistic technique for simultaneous localization
and door state estimation with mobile robots in
dynamic environments. In IROS-2002.
Thrun, S. 2000. Probabilistic Algorithms in Robotics.
School of Computer Science, Carnegie Mellon
University. Pittsburgh, PA.
M. Montemerlo, S. Thrun, D. Koller, and B. Wegbreit.
2002. FastSLAM: A factored solution to the
simultaneous localization and mapping problem. In
AAAI-02.
Thrun, S.; Fox, D.; Burgard, W.; and Dellaert, F. 2001.
Robust Monte Carlo Localization for Mobile
Robots. Artificial Intelligence Magazine.
J.Liu and R. Chen. 1998. Sequential monte carlo
methods for dynamic systems. Journal of the
American Statistical Association 93:1032-1044.
Borenstein, J.; Everett, B.; and Feng, L. 1996. Navigating
Mobile Robots: Systems and Techniques. A.K.
Peters, Ltd. Wellesley, MA.
Thrun, S.; Fox, D.; and Burgard, W. 2000. Monte
Carlo Localization with Mixture Proposal
Distribution. In Proceedings of the AAAI National
Conference on Artificial Intelligence, Austin, TX.
Thrun, S. 2002; Particle Filters in Robotics. In
Proceedings of Uncertainty in AI 2002.
M. I. Jordan, Z. Ghahramani, T. S. Jaakkola, and L. K.
Saul. In M. I. Jordan (Ed.); An introduction to
variational methods for graphical models. Learning in
Graphical Models, Cambridge: MIT Press, 1999.
Fox, D.; Burgard, W. and Thrun, S.; Markov Localization
for Mobile Robots in Dynamic Environments. In
Journal of Artificial Intelligence Research, 1999.
Hähnel, D.; Triebel, R.; Burgard, W. and Thrun, S.; Map
building with mobile robots in dynamic environments.
In ICRA, 2003.
Thrun, S.; Burgard W.; Fox, D.; Probabilistic Robotics.
Cambridge: MIT Press, 2005.
LOCALIZATION WITH DYNAMIC MOTION MODELS - Determining Motion Model Parameters Dynamically in
Monte Carlo Localization
127
