Analysing the Woo-Lam protocol using CSP and rank

functions

Siraj Shaikh and Vicky Bush

Department of Multimedia and Computing,

University of Gloucestershire Business School,

Park Campus, Cheltenham Spa, GL52 2RH, UK

Abstract. Designing security protocols is a challenging and deceptive exercise.

Even small protocols providing straightforward security goals, such as authenti-

cation, have been hard to design correctly, leading to the presence of many sub-

tle attacks. Over the years various formal approaches have emerged to analyse

security protocols making use of different formalisms. Schneider has developed

a formal approach to modeling security protocols using the process algebra

CSP. He introduces the notion of rank functions to analyse the protocols. We

demonstrate an application of this approach to the Woo-Lam protocol. We de-

scribe the protocol in detail along with an established attack on its goals. We

then describe Schneider’s rank function theorem and use it to analyse the proto-

col.

1 Introduction

Over the years various formal approaches have emerged to analyse security protocols

[8], making use of different formalisms including logic [3,11] strand spaces [12], type

theory [4], model-checking [5,7] and some hybrid techniques [6]. A main aspect of

this research is the perfect-encryption assumption that allows cryptography to be

treated as a black-box and therefore flawless; this is formalised by Dolev and Yao [1].

Schneider [10] has developed a formal approach to modeling security protocols using

CSP [2]. Schneider then proceeds to introduce the notion of rank functions to analyse

the protocols.

The purpose of this paper is to demonstrate an application of this approach to the

Woo-Lam protocol [13]. The protocol is an example of an authentication protocol

with a history of established attacks. We describe the Woo-Lam protocol in Section 2,

along with an attack in Section 2.1. We then describe Schneider’s CSP approach and

model the Woo-Lam protocol in CSP in Section 3. We introduce the rank functions

approach in relevant detail and apply the approach to the Woo-Lam protocol in Sec-

tion 4. We finally discuss our experiences of this effort to conclude the paper in Sec-

tion 5.

Shaikh S. and Bush V. (2005).

Analysing the Woo-Lam protocol using CSP and rank functions.

In Proceedings of the 3rd International Workshop on Security in Information Systems, pages 3-12

DOI: 10.5220/0002557000030012

 SciTePress

2 Woo-Lam protocol

Woo and Lam [13] introduce a protocol that provides one-way authentication of the

initiator of the protocol, A, to a responder, B. The protocol uses symmetric-key cryp-

tography and a trusted third-party server, with whom A and B share long-term sym-

metric keys.

(1) A → B : A

(2) B → A : N

(3) A → B : {N

}

KAS

(4) B → S : {A,{N

}

KAS

}

KBS

(5) S → B : {N

}

KBS

Fig. 1. Woo-Lam protocol

The protocol is shown in Fig. 1 above where {m}

represents message m encrypted

under key k and “,” represents the concatenation operator. The keys K

and K

rep-

resent the long-term keys that A and B share with the trusted server S. The protocol

goal is to authenticate A to B by using a fresh and unpredictable nonce, N

, produced

by B.

A starts the protocol by sending it’s identity to B. B replies by sending a freshly

generated nonce N

. A encrypts N

with key K

and sends it back to B. B concatenates

A’s reply with the identity of A, encrypts it with key K

and sends it to the server S. S

sends out N

back to B encrypted under K

. B compares the nonce it receives from S

with the one it sent out to A. If they match, then B is guaranteed that the initiator of the

protocol is in fact the principal claimed in the first step of the protocol.

2.1 An attack on the Woo-Lam protocol

The Woo-Lam protocol has been to shown to be susceptible to a few attacks [14], one

of which is shown in Fig. 2 below.

(1.1) I(A) → B : A

(1.2) B → I(A) : N

(1.3) I(A) → B : X

(2.1) I → B : I

(2.2) B → I : N

′

(2.3) I → B : {N

}

KIS

(1.4) B → S : {A,X}

KBS

(2.4) B → S : {I,{N

}

KIS

}

KBS

(1.5) S → B : {N

}

KBS

Fig. 2. An attack on the Woo-Lam protocol

The attack shows two simultaneous inbound authentication attempts initiated by an

intruder I, where I is also considered as any other regular participant. I pretends to be

A in one (1.x) and retains its own identity I for the other (2.x). I obtains nonces from B

for both runs and encrypts the nonce N

intended for A with its own server key and

returns it to B, retaining its original identity. When the nonce is returned by the server,

it leads B to believe that it has authenticated A, whereas A has not even participated in

either of the runs. The attack is complete.

The attack shown in Fig. 2 demonstrates the difficulty in designing such protocols

and emphasises the need for a formal and rigorous analysis of these protocols.

3 Schneider’s CSP approach

In order to deal with the problem highlighted in the previous section, Schneider pre-

sents a formal framework that uses the process algebra CSP to model protocols. We

present Schneider’s CSP approach in detail, describing the relevant syntax for CSP

and its trace semantics in Section 3.1. In Section 3.2 we model the participants in the

Woo-Lam protocol as CSP processes and specify a network composed of these proc-

esses. We then present a trace specification that the network needs to satisfy for the

protocol to hold correct. Finally we adopt a proof strategy to verify this network.

While we discuss this notation in detail relevant to our usage in this paper, we take

for granted the reader’s basic knowledge of CSP and its use by Schneider [10] to

model security protocols; in-depth treatments of CSP are provided by Hoare [2] and,

more relevantly, Ryan, et al [8].

3.1 CSP Events and Processes

A CSP system is modelled in terms of processes and events that these processes can

perform, which are essentially instances of communication, usually involving a chan-

nel and some data value. Events may be atomic in structure or may consist of distinct

components. The CSP expression a → P describes a process P with event a in the

interface of P. The process is initially able to perform a and then behaves as P. The

process STOP is the simplest CSP process that can be described; it has no event tran-

sitions and does not engage in any events. A choice operator

 provides the option for

running either of the two processes, P and Q for example, when put together as P

 Q

whereas P and Q running in parallel would be written as P

Q where both P and Q

have to synchronise on events in a set of events A. If P or Q were to perform any

events that are not in A then they can do so independently without the need for any

synchronisation. Another form of a parallel composition could be P Æ Æ Æ Q where P and

Q do not need to interact with each other at all, known as interleaving. A process

could be restricted on certain events, such as P

STOP where all of P’s occurrences

of events from A are restricted; P would not be able to perform any events in A.

For the purpose of communication, a process may have channels using which it

communicates, accepts inputs on or produces output on. The expression c!v → P

describes a process that will output the value of v on the channel c and then behave as

P. A process P accepting an input x on the channel c is described as c?x → P(x) where

the behaviour of P after the input is described as P(x), determined by the input. To

express message transmission and reception, Schneider [10] introduces two new chan-

nels, send and receive, which are public channels that all processes use to send and

receive messages on. The events are structured as send.i.j.m where a message m is sent

by source i to destination j on the channel send while receive.j.i.m represents a mes-

sage m being received by j from a source i on the channel receive.

3.1.1 Trace Semantics

The trace semantics in CSP allows us to capture the sequence of events performed by

a communicating process as a trace and then use the trace to model the behaviour of

the process. A trace tr of all events possibly performed by a process P could be ex-

pressed as tr = traces(P). An example of a trace could be „a, bÒ where event a is per-

formed followed by event b, whereas „Ò is an empty trace.

A concatenation of two traces tr

and tr

would be written as tr

^ tr

, which is the

sequence of evens in tr

followed by the sequence of events in tr

. A trace tr could be

of the form „aÒ ^ tr′ where event a is followed by tr′, the remainder of the trace. A

subsequence of tr could be expressed as tr′ ¯ tr where tr′ is the prefix of tr. Traces

also provide a projection operation where the tr á A is the maximal subsequence of tr,

all of whose events are drawn from a set of events A.

Trace semantics are used by Schneider [9] to specify security properties for proto-

cols as trace specifications. These are essentially defined as predicates on a trace of a

process. This is done by defining a predicate on traces and checking whether a process

satisfies the trace specification for its every trace. For a process P and a predicate

S(tr) on a trace tr

P sat S(tr) ⇔ ∀ tr ∈ traces(P) • S(tr)

signifies that P satisfies S(tr) if S(tr) holds for every trace of P.

3.2 Modelling the network

We now model the Woo-Lam protocol in CSP as a network and specify the authenti-

cation property for this network as a trace specification. We then describe the proof

strategy to verify this network for the given trace specification.

While modelling the different processes of a protocol, Schneider [8] takes advan-

tage of the extensibility of CSP to introduce additional control events known as sig-

nals. These signal events are then used in trace specifications to express the authenti-

cation goals of a protocol. We model the three participant roles in the Woo-Lam pro-

tocol in CSP below

Initiator

= 

send.A.b.A →

receive.A.b.n

→

Running.A.b.n

→

send.A.b.{n}

KAS

→ Stop

Server = receive.S.b.{a,{n}

Kas

}

Kbs

→

send.S.b.{n}

Kbs

→ Stop

Responder

) = receive.B.a.a →

send.B.a.n

→

receive.B.a.{n

}

Kas

→

send.B.s.{a,{n

}

Kas

}

KBS

→

receive.B.s.{n

}

KBS

→

Commit.B.a.n

→ Stop

In the model above, we specify a Running.A.b.n signal and introduce it in A’s run,

indicating that A is aware of its involvement in a run with b and the nonce n being

used as part of this run. We specify a corresponding Commit.B.a.n

signal on B’s

behalf indicating that B has completed the protocol run and authenticated a using

nonce n

. The Commit.B.a.n

signal is placed at the end of B’s run as it is only when B

receives the final message from S it can be assured of A’s involvement in the run. The

entire network is composed of the above processes along with an Intruder process that

is assumed to be in complete control of the network. In order to model it as such, we

specify our NET as where Initiator

, Responder

and Server all communicate with

each other only through an Intruder process and consider a specific run of the protocol

between Initiator

and Responder

using the nonce N

NET = (Initiator

Æ Æ Æ Responder

) Æ Æ Æ Server) Æ Æ Intruder

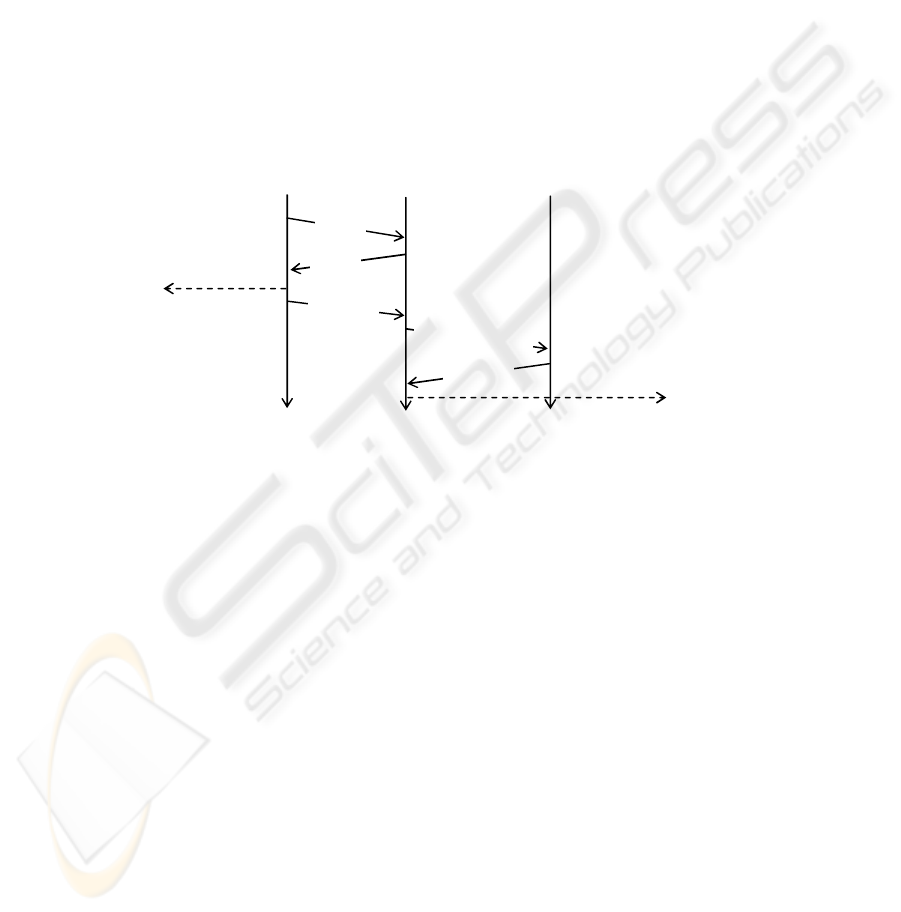
We show this specific run of the protocol with appropriate signals in Fig. 3 below.

Fig. 3. A specific run of the Woo-Lam protocol involving A and B using nonce N

Proof strategy. We now specify a trace specification that expresses the authentication

property needed to be satisfied by this NET. We use the signal events for the particu-

lar run shown in Fig. 3 and consider trace tr to be some trace of NET then

tr′^„Commit.B.A.N

Ò ¯ tr ﬁ Running.A.B.N

in tr′

In other words, if Commit.B.A.N

is in tr then so is Running.A.B.N

, preceding it. If

the NET could be proved to satisfy this specification, then the protocol is proved

correct for the property of authentication. In order to prove that the NET meets the

trace specification, we restrict NET on the event Running.A.B.N

and check the result-

ing NET for the occurrence of the event Commit.B.A.N

. The restricted NET should

not allow Commit.B.A.N

to occur in its trace tr

NET

unning.A.B.N

Stop sat tr á Commit.B.A.N

= „Ò

Running.A.B.N

Commit.B.A.N

Initiator

Responder

) Server

{A,{N

}

KAS

}

KBS

}

KAS

}

KBS

4 Analysing the Woo-Lam

In the previous section, we have built a CSP system along with a trace specification

that the system needs to satisfy. To verify the system for such a specification, Schnei-

der introduces the notion of a rank function [10]. We introduce the idea along with the

central rank function theorem [10] in Section 4.1. In Section 4.2, we construct a rank

function for the Woo-Lam protocol and evaluate the different conditions provided in

the theorem to judge the correctness of the protocol.

4.1 Rank functions

Consider the set of participant identities on the network to be U, the set of nonces

used by the participants in protocol runs as N and a set of encryption keys used as K.

The set of all such atoms is A, where the atoms are defined as A = U U N U K. We

consider a message space M to contain all the messages and signals that may appear

during a protocol’s execution, such that m ∈ A ⇒ m ∈ M.

Schneider [10] defines a rank function ρ to map events and messages to integers ρ:

fZ. The message space is then divided into two parts where

= {m ∈ M | ρ(m) ¯ 0} M

ρ+

= {m ∈ M | ρ(m) > 0}

The purpose of this partition of the message space is to characterise those messages

that the intruder might get hold of without compromising the protocol – assigned a

positive rank – and those messages that the enemy should never get hold of – assigned

a non-positive rank. It is desirable for a process never to transmit a message of non-

positive rank. For a certain process P to maintain positive rank, it is understood that it

will never transmit a message with a non-positive rank unless it has previously re-

ceived a message with a non-positive rank. The process P is said to maintain positive

ρ, if

P sat receive. U. U. M

precedes send. U. U. M

The process P satisfies the condition that if it transmits a message of non-positive

rank (send. U. U. M

represents the transmission of a non-positive message, M

from and to any participant U) then it has to have received a message of non-positive

rank earlier, represented by receive. U. U. M

. It is not important who the message

is received from or is sent to.

Schneider also [10] introduces a generates ‘H’ relation to simulate cryptographic

functionality on behalf of an attacker. We use the relation to model encryption and

decryption of messages or simpler transformations such as concatenation of messages.

This relation, however, can be extended to model various cryptographic operations,

the details of which are available in [10]. A rank function theorem [10] is then used to

analyse such a rank function and verify that a trace specification is always met in all

possible runs of the protocol. We consider tr to be some trace of the NET as defined

in Section 3.2.

Rank function theorem. If, for sets R and T, there is a rank function ρ: M f Z satis-

fying

R1) ∀ m ∈ IK • ρ(m) > 0

R2) ((∀ s ∈ S • ρ(s) > 0) ∧ S H m) ⇒ ρ(m) > 0

R3) ∀ t ∈ T • ρ(t) ¯ 0

R4) i ∈ U • User

Stop sat maintain positive ρ

Then NET

Stop sat tr á T = „Ò

The theorem, the proof of which is available in [10], essentially states that if the

rank function, and therefore the underlying NET, satisfies the four properties, then no

secret messages of non-positive rank, denoted by set T, can be produced. In particular,

the Intruder should not be able to generate any illegal messages from the messages it

knows at the beginning of the protocol, and denoted by the set Initial Knowledge, IK,

nor from the messages it sees during the protocol execution. Also, honest participants

should not be able to generate any illegal messages unless they are sent one, that is,

they maintain positive ρ while being restricted on events in set R. The actual verifica-

tion of the theorem conditions is performed manually for every rank function con-

structed for a protocol. We now use this approach to analyse the Woo-Lam protocol.

4.2 Constructing the rank function

We identify the ranks on the message space for our NET and construct the rank func-

tion shown in Fig. 4 below. The rank function we have constructed assigns all user

identities in the set U a positive rank. The identity of all users is assumed to be known

to the Intruder and therefore could be impersonated by the intruder. All the nonces in

the set N, including N

, are assigned a positive rank. B sends out N

in cleartext and

therefore an Intruder can get hold of the nonce without further ado. The two shared

keys used in the protocol, K

and K

, are both assigned a non-positive rank as they

are supposed to be private to A and B. As the NET is restricted on the event Run-

ning.A.B.N

, the three messages (see Fig. 3) that follow this event, {N

}

KAS

{A,{N

}

KAS

}

KBS

and {N

}

KBS

, should not appear in the restricted NET either. We as-

sign these three messages a non-positive rank along with signal event Commit.B.A.N

which logically follows these three messages.

ρ(U) = 1 (including A, B and S)

0 if k = K

ρ(K) = or k = K

1 otherwise

ρ(N) = 1 (including N

)

0 if {m}

= {N

}

KAS

or {m}

= {A,{N

}

KAS

}

KBS

ρ({m}

) = or {m}

= {N

}

KBS

1 otherwise

ρ(Running.A.B.N

) = 1 ρ(Commit.B.A.N

) = 0

Fig. 4. A rank function for the Woo-Lam protocol

Recall that the rank function theorem is defined in terms of general sets R and T.

For our analysis, we assign the single event Running.A.B.N

to set R and assign the

single event Commit.B.A.N

to set T. This corresponds to the proof strategy described

in Section 3.2, where we need to check for the occurrence of Commit.B.A.N

in a

NET restricted on Running.A.B.N

. We now consider each of the conditions of the

rank function theorem and check whether our rank function satisfies them.

R1) ∀ m ∈ IK • ρ(m) > 0

The set IK contains all the agent identities and a key K

shared between I and S. There

is nothing in this set that is of non-positive rank. The condition is deemed satisfied.

R2) ((∀ s ∈ S • ρ(s) > 0) ∧ S H m) ⇒ ρ(m) > 0

This conditions checks whether a message of non-positive rank can be generated un-

der the ‘H’ relation from a set of messages of positive rank. None of the messages

identified as of positive rank, shown in Fig. 4, let the Intruder generate any messages

that are of non-positive rank. The three messages of non-positive rank, {N

}

KAS

{A,{N

}

KAS

}

KBS

and {N

}

KBS

, are encrypted under keys K

and K

both of which are

of non-positive rank. This prevents the Intruder from generating these messages as the

Intruder has no way of acquiring these two keys. The condition is deemed satisfied.

R3) ∀ t ∈ T • ρ(t) ¯ 0

This condition requires none of the events in T to be of positive rank. The only event

in set T is the signal event Commit.B.A.N

of non-positive rank. This condition is

deemed satisfied.

R4) i ∈ U • User

Stop sat maintain positive ρ

For this condition to be satisfied every process in the NET needs to maintain positive

ρ while being restricted on the events in set R, where R = {Running.A.B.N

}. We

consider processes Initiator

, Responder

and Server, restrict them on Run-

ning.A.B.N

and check whether they maintain positive ρ. Since only Initiator

can

perform Running.A.B.N

, the other two processes remain unaffected. The restriction

on Initiator

simplifies to

Initiator

unning.A.B.N

Stop =



send.A.b.A →

receive.A.b.n

→

if b = B ∧ n = N

then Stop

else Running.A.b.n

→

send.A.b.{n}

KAS

→ Stop

In the choice operator 

, b indicates the other participants that Initiator

may

communicate with. If participant b = B and the nonce n = N

then we instruct Initia-

tor

to Stop. Any other participant instead of B or even a different nonce then N

would allow Initiator

to continue as normal.

Upon inspection, we observe that Initiator

unning.A.B.N

Stop fails to maintain

positive ρ. In terms of protocol runs, consider a run where A initiates the protocol with

a participant other than B (and I intercepts) as shown in Fig. 5 below

(1) A → I(C) : A

(2) I(C) → A : N

(3) A → I(C) : {N

}

KAS

Fig. 5. A possible run of the protocol

In this case, the process Initiator

unning.A.B.N

Stop behaves as follows

send.A.C.A →

receive.A.C.N

→

if b = B ∧ n

= N

then Stop

else Running.A.C.N

→

send.A.C.{N

}

KAS

→ Stop

A outputs the message {N

}

KAS

while communicating with another participant C.

The message {N

}

KAS

is of non-positive rank as shown in Fig 4. This shows that A

does not maintain positive ρ despite the restriction on it and the protocol, therefore,

fails to meet the trace specification presented in Section 3.2. The theorem has been

successful in finding a flaw in the Woo-Lam protocol, the existence of which we al-

ready demonstrated earlier in Section 2. Note that the failure of a rank function to

satisfy the conditions of the theorem signifies a flaw in the protocol but it may not

always be possible to construct an attack. It does, however, provide an insight into the

workings of a protocol, which is often enough to lead to the discovery of an attack.

5 Conclusion

While this approach provides a formally meticulous analysis, the process of identify-

ing a rank function is non-trivial. Once a rank function is constructed, however, it

gives confidence in the soundness of the protocol design. We have applied this theo-

rem to the Woo-Lam protocol to expose any flaws in the design and have managed to

identify the attacks discussed earlier successfully.

We recommend this approach for thorough investigation of similar protocols. The

process of finding a rank function requires intuitive understanding of such protocols

and focuses attention on relevant design aspects of these protocols.

References

1. D. Dolev and A. C. Yao, “On the security of public key protocols”, IEEE Transactions on

Information Theory, 29(2), March 1983, pp. 198-208

2. C. A. R Hoare, Communicating Sequential Processes, Prentice-Hall International, 1985

3. L. Gong, R. Needham and R. Yahalom, “Reasoning about Belief in Cryptographic Proto-

cols”, In IEEE Symposium on Research in Security and Privacy, IEEE Computer Society

Press, May 1990, pp. 234–248

4. A. D. Gordon and A. Jeffrey, “Authenticity by typing for security protocols” In 14th IEEE

Computer Security Foundations Workshop, 2001, pp. 145-159

5. G. Lowe, “Breaking and Fixing the Needham-Schroeder public-key protocol using FDR”,

Proceedings of TACAS, LNCS 1055, 1996, Springer-Verlag, pp. 147-166

6. C. Meadows “The NRL Protocol Analyzer: An overview”, Journal of Logic Programming,

26(2), 1996, pp. 113-131

7. J. C. Mitchell, M. Mitchell and U. Stern, “Automated analysis of cryptographic protocols

using Murϕ”, In IEEE Symposium on Security and Privacy, IEEE Computer Society Press,

1997, pp. 141-151

8. P. Ryan, S. Schneider, M. Goldsmith, G. Lowe and B. Roscoe, B. Modelling and Analysis

of Security Protocols. Addison-Wesley, 2001

9. S. Schneider, “Security Properties and CSP”, In IEEE Symposium Research in Security and

Privacy, Oakland, IEEE Computer Society Press, 1996

10. S. Schneider, “Verifying Authentication Protocols in CSP”, IEEE Transactions on Soft-

ware Engineering, Volume 24, No. 9, IEEE Computer Society Press, September 1998, pp.

741-758

11. P. F. Syverson and P. C. van Oorschot, “On unifying some cryptographic protocol logics”,

In IEEE Symposium on Research in Security and Privacy, IEEE Computer Society Press,

May 1994, pp. 14-28

12. F. J. Thayer Fábrega, J. C. Herzog and J. D. Guttman, “Strand spaces: Why is a security

protocol correct?”, In IEEE Symposium Research in Security and Privacy, IEEE Computer

Society Press, May 1998, pp. 24-34

13. T.Y.C. Woo and S. S. Lam, “Authentication for Distributed Systems”, Computer, 25(1),

January 1992, pp. 39-52

14. T.Y.C. Woo and S. S. Lam, “A lesson on Authenticated Protocol design”, Operating Sys-

tems Review, 28(3), 1994, pp. 24-37