SITUATION ASSESSMENT WITH OBJECT ORIENTED

PROBABILISTIC RELATIONAL MODELS

Catherine Howard*, Markus Stumptner**

*Electronic Warfare and Radar Division, Defence Science and Technology Organisation

PO Box 1500, Edinburgh, South Australia, 5111

**Advanced Computing and Research Centre, University of South Australia, Adelaide, South Australia, 5095

Keywords: Bayesian Networks, Decision Support Systems, Industrial Applications of Artificial Intelligence

Abstract: This paper presents a new Object Oriented Probabilistic Relational language whi

ch is built upon the Bangsø

Object Oriented Bayesian Network framework. We are currently studying the application of this language

for situation assessment in complex military and business domains.

1 INTRODUCTION

Decision making in time-critical, high stress,

information overloaded environments, such as the

tactical military domain, is a complex research

problem that can benefit from the application of

information fusion techniques. Information fusion is

the process of acquiring, aligning, correlating,

associating and combining relevant information

from various sources into one or more

representational formats appropriate for interpreting

the information. The Lambert revision (Lambert

2003) (λJDL) of the widely accepted Joint Directors

of Laboratories, or JDL, model (Steinberg, Bowman

et al. 1998) provides a functional model of the

information fusion process. λJDL divides the

information fusion into three sub-processes: object,

situation and impact fusion. This paper focuses on

Situation Fusion.

Within the λJDL

model, Situation Fusion is

defined as the process of utilizing one or more data

sources over time to assemble a representation of the

relationships of interest between objects of interest

in the area of interest in the battlespace.

Relationships of interest can include physical,

temporal, spatial, organizational, perceptual and

functional relationships. The relationships

meaningful to a user will be highly dependent on the

domain and the user’s intentions. A Situation

Assessment is defined as a persistent representation

of the relationships of interest.

While significant progress has been made in

Obj

ect Fusion, substantial challenges remain in

Situation and Impact Fusion (Llinas 2001; Sycara

and Lewis 2002; Lambert 2003; Salerno, Hinman et

al. 2003). One such challenge is the formalization of

the computational processes at these levels.

Formulating Situation Assessments from sensor

ata requires the ability to represent:

• Objects a

nd their attributes

• Relatio

nships and their attributes

and the ability to:

• Fu

se information at various levels of

abstraction

• Perform

temporal reasoning

• H

andle the uncertainty about:

o Th

e identity, number, location and attributes

of objects

o Th

e existence and attributes of relationships

1.1 Example Scenario

A classic situation assessment example is a tactical

military scenario where a helicopter is flying along a

planned route. The intent of the pilots is to arrive

safely at the target without being seen, acquired or

targeted by an adversary’s radar installations or shot

down by any weapon systems known to be co-

located with the radar installations. There are an

unknown number of land based friendly and

adversary radar and weapon installations in the area.

Onboard the helicopter is a suite of sensing systems

which collect and analyze emissions from the radars

during the flight, but provide only a partial picture of

the battle space. The data may be incomplete,

incorrect, contradictory or uncertain. It may have

various degrees of latency and may be affected by

the environment or by enemy deception or

412

Howard C. and Stumptner M. (2005).

SITUATION ASSESSMENT WITH OBJECT ORIENTED PROBABILISTIC RELATIONAL MODELS.

In Proceedings of the Seventh International Conference on Enterprise Information Systems, pages 412-418

DOI: 10.5220/0002538904120418

 SciTePress

confusion, which creates false or misleading data.

The most important relationships of interest, given

the pilot’s intent, include the helicopter approaching,

receding from or traversing the detection range of a

radar or the lethality envelope of a weapon system.

In order to successfully complete the mission, the

pilot must develop an understanding of which, if

any, of these relationships exist at any given time

and the impact the existing relationships will have

on the mission objectives.

Counterparts to this competitive scenario in the

business domain are numerous, although spatial

relationships play little or no role; the threats are

competitor’s actions in the business environment

and the strategic choices correspond to business

decisions

1.2 The Road to OOPRMs

Bayesian Networks (BN) have been used in many

existing decision support systems, e.g., to reason

about causal and perceptual relationships between

objects in the battlespace in tactical military

reasoning (Laskey and Mahoney 1997; Mulgund,

Rinkus et al. 1997; Gonsalves and Rinkus 1998;

Jones, Hayes et al. 1998; Gonsalves, Rinkus et al.

1999; Das, Grey et al. 2002; Wright, Mahoney et al.

2002). However, BN have been shown to be

inadequate for reasoning about large, complex

domains (Pfeffer 1999) because of their lack of

flexibility, the fact that they are static models and

their inability to take full advantage of domain

structure or reuse. The lack of flexibility is of

particular importance to situation assessment domain

because the variables relevant to reasoning about a

situation will be dependent on the domain and the

user intentions.

We aim to use automated reasoning to derive

Situation Assessments from signal data to provide

dynamic decision support to decisionmakers such as

managers or tactical military commanders. In order

to do this, we need to represent and reason about the

location, status and the relationships which exist

between objects in the domain of interest (e.g., the

battlespace or market) given the input data (e.g.,

sensors or market reports). From the preceding

discussion of the limitations of BN in the domain, it

is clear that a technique is required which can allow

the random variables in the model, their state spaces

and their probabilistic relationships to vary over time

and from instance to instance. First Order

Probabilistic Languages (FOPLs) are languages

which combine probability theory with the

expressive power of first order logic. Recently,

FOPLs have been used in a number of domains such

as military situation awareness (Pfeffer 1999),

hypertext classification (Getoor 2002) and traffic

surveillance (Pasula 2003). Probabilistic Relational

Models (PRM) are a family of FOPL. The thesis

behind this work is that FOPL in the form of OPRM

will provide a flexible and practical approach to

reasoning in complex domains such as military

Situation Assessment. And that using such a

language will formalize the computational processes

at this stage of the information fusion process

2 PROBABILISTIC RELATIONAL

MODELS

Probabilistic Relational Models (PRM) (Koller and

Pfeffer 1998; Getoor 2002) extend traditional

attribute based Bayesian Networks with the concepts

of objects, their attributes and relationships between

them. The most important difference between BN

and PRM is that PRM define the dependency model

at the class level. The class dependency model is

then instantiated for any instance of the class.

PRM annotate frames with a probability model

representing the uncertainty over the properties of an

instance, capturing both its probabilistic dependence

on its own attributes and the attributes of related

instances. PRM specify a template for the

probability distribution over a knowledge base

(Getoor 2002). This template consists of two parts:

a relational component and a probabilistic

component. The relational component describes

how the classes in the domain are related. The

probabilistic component details the probabilistic

dependencies between attributes in the domain. A

PRM can also represent uncertainty over the

structure of the model.

PRM were created by integrating a frame-based

representation with the only OOBN framework

known at the time; Koller and Pfeffers OOBN

framework (hereafter referred to as KPOOBN).

However, recent work by Bangsø (Bangso and

Wuillemin 2000; Bangso 2004) has proposed a new

framework for OOBN (hereafter referred to as

BOOBN) which has several advantages over Koller

and Pfeffer’s OOBN framework.

Both KPOOBN and BOOBN frameworks define

an OOBN class as a BN fragment containing output,

input, and protected (or encapsulated) nodes. The

input and output variables form the interface of the

class. The interface encapsulates the internal

variables of the class, d-separating them from the

rest of the network. All communication with other

instances is formulated in terms of probability

statements over the instance’s interface.

The main difference between the two

frameworks is that BOOBN introduce the use of

SITUATION ASSESSMENT WITH OBJECT ORIENTED PROBABILISTIC RELATIONAL MODELS

413

reference nodes and reference links to overcome the

problem that no node inside a class can have parents

outside the class. A reference node is a special type

of node pointing to a node in another scope (called

the referenced node). A reference node is bound to

its referenced node by a reference link. BOOBN

define all input nodes to be reference nodes.

While these reference nodes create an additional

computational cost, they provide several important

benefits. For example, the reference nodes enable

BOOBN framework to have a more intuitive

definition of inheritance in the modeling domain.

KPOOBN inheritance definition corresponds to

contravariance while Bangsø’s definition

corresponds to covariance. The reference nodes also

allow the BOOBN framework to compactly

represent dynamic situations, whereas KPOOBN, as

it stands, does not have the expressive power to deal

with situations that evolve over time (Koller and

Pfeffer 1997). These reference nodes also provide

an advantage during inference, as outlined in Section

3 OBJECT ORIENTED PRM

Following the example set by Koller and Pfeffer’s

PRM, we have integrated a frame based

representation system with the BOOBN framework.

Throughout the remainder of the paper, the

University example shown in Figure 1 will be used

to illustrate the discussion. We decided to use this

relatively “unthreatening” business domain to

simplify the exposition and avoid the complexities

of identity uncertainty (discussed in Section 7). The

following definitions expand (Getoor 2002).

Definition 3.1: OPRM (like PRM) consist of a

relational component and a probabilistic component.

The relational component consists of:

• A set of classes, C ={C

, C

,…, C

}, and possibly

a partial ordering over C which defines the class

hierarchy. The set of classes in the University

example is C = {Lecturer, Paper, Conference,

Promotion Evaluation}.

• A set of descriptive attributes for each class C in

C. C

.A is an attribute A of class C

. Each s

descriptive attribute A has a domain type

Dom[A]∈C and a range type Range[A]=Val[A]

where Val[A] is a predefined finite enumerated set

of values. The set of descriptive attributes of class

C is denoted A(X). In the University example,

A(Lecturer)={Tired, Productivity, Teaching

Skills, Brilliance, Quantifier(Papers) and

WillGetPromoted}. The Productivity attribute of

the Lecturer class has Val[Productivity] = {low,

medium, high}.

• A set of reference attributes ρ for each class C in

C. C

.ρ is a reference attribute ρ of class C

Reference attributes represent functional

relationships between instances in the knowledge

base (i.e. they are attributes which reference other

frame instances). Each reference attribute ρ has a

domain type Dom[ρ]∈C and a range type

Range[ρ]∈C for some class C in C. Each

reference attribute (except uncertain reference

attributes) have an inverse, which is interpreted as

the inverse function of ρ. In our University

example, the Paper class has a single valued

reference attribute Conference whose value is an

instance corresponding to an instance of the

Conference class. The set of reference attributes

of class C is denoted R(X). In the University

example, R(Paper)={Conference, Promotion

Evaluations}.

• A set of named instances, I, which represent

instantiations of the classes. As multiple

inheritance is not accommodated in this

framework, each instance is an instance of only

one class.

The probabilistic component consists of:

• A set of conditional probability models P(A|Pa[A])

for the descriptive attributes, where Pa[A] is the

set of parents of A. These probability models may

be attached to particular instances or inherited

from classes because like PRM, OPRM define the

dependency model at the class level, allowing it to

be instantiated for any instance of that class.

The classes of the OPRM are organized into a

hierarchy. A frame’s slots and facets, including

their probability models, are inherited from the

frame’s superclass in the hierarchy. If required,

subclasses can redefine any inherited information of

any attribute including the probability model.

3.1 Inference in OPRM

Inference is performed on an instantiated OPRM by

constructing the ‘equivalent’ BOOBN for each class

by instantiating a node for each uncertain descriptive

attribute in the class. The protected nodes in these

equivalent BOOBN are encapsulated from the rest of

the model via the instances interface and the

inference algorithms take advantage of this fact.

3.2 Multi-Valued Reference

Attributes

Reference attributes do not necessarily represent

one-to-one relationships. These attributes can be

multi-valued, representing one-to-many and many-

to-many relationships. For example, the Paper

attribute in the Promotion Evaluations class is a

ICEIS 2005 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

414

multi-valued reference attribute. Each value the

attribute can take on is an instance of the Paper

class. But the parents of a descriptive attribute such

as Lecturer.WillGetPromoted must be descriptive

attributes. In order to allow descriptive attributes

such as Lecturer.WillGetPromoted to depend on

attributes of related instances where the relations is

multi-valued, an aggregate attribute is introduced

into the frame containing the multi-valued attribute.

Aggregate attributes allow descriptive attributes

such as Lecturer.WillGetPromoted to depend on

the set of instances via an aggregate property of the

set, rather than each individually related instance.

Definition: An aggregate attribute γ(ρ) is a

descriptive attribute which summarizes a property of

a set of related instances. Attributes other than

aggregate attribute cannot depend directly in a multi-

valued reference attributes.

An aggregate attribute is represented in the

equivalent BOOBN by a simple node. As a

descriptive attribute, an aggregate attribute has a set

of parents, which includes each related instance, and

a distribution that specifies the conditional

probability over its values, given the values of its

parents

In our university example, the aggregate attribute

QuantifierPapers is true if and only if more than 5

papers have a high impact, i.e. true if ≥

5(Papers.Impact:high). In this case the value of

the aggregate attribute is {true, false}. Because an

aggregate attribute is a descriptive attribute, it can be

a parent of another attribute. For example,

Lecturer.Quantifier(Papers) is a parent of

Lecturer.WillGetPromoted

4 THE UNIVERSITY EXAMPLE

The University example model is the simplest form

of OPRM, where the complete relational structure

(i.e. the set of objects and relationships between

them) is known. Given the relational structure, the

OPRM specifies a probability distribution over the

attributes of the instances in the model. We are

employing the unique names assumption in this

example, which means that each object in the

knowledge base is assumed to have a unique

identifier (i.e. identity uncertainty is not present).

The OPRM shown in Figure 1 evaluates the

promotion prospects of university academics based

upon their teaching skills, brilliance and productivity

and the impact of their publications. The impact of

their publications are effected by the standard and

prestige of the conferences to which they were

submitted and is summarized by the aggregate node

Quantifier(Papers).

In the diagram, the red nodes indicate output

nodes while the dashed nodes represent input nodes.

Together input and output nodes define the

interfaces, Int, of the various classes. For example,

the interface for the

Lecturer class Int(Lecturer) =

{Quantifier(Papers), Brilliance, Will-GetPromoted}.

The interface for the Paper class is Int(Paper) =

{Brilliance, Standard, Prestige,Impact}. The interface

for the Conference class is Int(Conference) =

{Standard, Prestige} while the interface for the

Promotion Evaluations class is Int(Promotion

Evaluations) = {Quantifier(Papers), Brilliance}.

Figure 1: The university OPRM. The model contains one

instance of the Lecturer class, ten instances of the Papers

class and ten instances of the Conferences class

5 TECHNIQUES FOR

REPRESENTING

UNCERTAINTY

The OPRM framework (like PRM) can be extended

to accommodate uncertainty about the relational

structure of the model. In these cases, the

uncertainty in the relational structure needs to be

explicitly modeled in the OPRM. The following

techniques (adapted from (Koller and Pfeffer 1998;

Pfeffer, Koller et al. 1999; Getoor 2002)) are useful

when the knowledge about the relational structure is

not complete

5.1 Structural Uncertainty

There are three types of structural uncertainty;

number, reference and identity uncertainty. The

techniques used to extend OPRM to accommodate

the first two types will be discussed in this section.

As we do not yet have techniques to accommodate

identity uncertainty into OPRM, it is discussed

further in Section 7

SITUATION ASSESSMENT WITH OBJECT ORIENTED PROBABILISTIC RELATIONAL MODELS

415

5.2 Number Uncertainty

Number uncertainty is present when it is unclear

how many values a multi-valued reference attribute

can take. For example, it may be uncertain how

many papers the lecturer Dr Smith has written.

Number uncertainty allows the set of instances in the

model to be varied.

Number uncertainty is integrated into the

probabilistic model of a class by introducing a

number attribute.

Definition: A number attribute num(ρ) is a

descriptive attribute with the range equal to the set

of integers {0…n} where n is the upper bound.

Num(ρ) denotes the number of values of ρ.

A number attribute is represented in the

equivalent BOOBN by a simple node. As a

descriptive attribute, a number attribute has a set of

parents (e.g., num(Paper) could be dependant on

Lecturer.Productivity) and a distribution that

specifies the conditional probability over its values,

given the values of its parents.

Recall from Section 3.2 that multi-values

reference attributes require an aggregate node to be

introduced into the network. Under number

uncertainty, the value of the aggregate attribute will

depend on the number attribute as well as the value

of related instances. For example, the value of

DrSmith.Quantifier(Papers) will depend on the

number attribute DrSmith.num(Papers) and the

impact attribute of the set of related instances

Paper[1] through to Paper[10]

5.3 Reference Uncertainty

Reference uncertainty is uncertainty over the value

of a single-valued reference attribute. For example:

it may be uncertain which conference Paper[1] was

submitted to. That is, there is uncertainty over

which Conference frame instance the

Paper[1].Conference reference attribute refers to.

In this case, which value of conference Prestige and

Standard should be used to determine the impact of

the paper? Reference uncertainty allows the

relationships between instances to be varied.

If C1.ρ (Paper.Conference) is an uncertain

reference attribute with domain C2 (Conference).

In the case of reference uncertainty, we need to

specify a probability model for the value of the

uncertain reference attribute C1.ρ. Instead of having

the OPRM specify a probability distribution directly

over the set of instances of C2 (i.e. Conference1-

Conference10), a technique introduced by (Getoor

2002) partitions the instances of C2 into subsets

using attributes of C2. The probability distribution

can then be specified over these partitions (which

encodes how likely the reference attributes value is

to fall into one partition versus another). Instances

are then selected uniformly from within these

partitions.

Thus reference uncertainty is integrated into the

probabilistic model of a class by associating each

uncertain reference attribute ρ of the class with a

selector attribute sel(ρ).

Definition: A selector attribute sel(ρ) is a

descriptive attribute where the values are a finite

enumerated set of frame instances. The partition

function (Getoor 2002) is defined as

:Y→Dom[Ψ

]. The values of the partition

function, ϕ, determine the subset of C2 from which

the value of ρ will be selected. The domain of the

selector attribute is Dom[Ψ

]. Thus the choice of

value for sel(ρ) determines the subset of C2 from

which the value of ρ is chosen. A partition function

has a set of partition attributes P[ρ] for of ρ. The

parents of sel(ρ) are those attributes/attribute chains

which influence the choice of a frame instance as the

value of ρ.

A selector attribute is represented in the

equivalent BOOBN by a simple node. In addition to

the selector attribute node, a multiplexor node is

introduced to the network. The set of parents for the

multiplexor node include the selector attribute and

all instances of the related frame (eg. the

Conference.standard node for each instance of

Conference). The multiplexor node uses the

probability distribution of the selector attribute to

select as its value the value of one of its other

parents.

To continue our University example, uncertainty

over which conference Paper[1] had been submitted

to would result in Paper[1].Accepted being

dependant on all possible combinations of

Conference.Standard values for the uncertain

Conference attribute. The value of

Paper[1].Conference could be one of several

Conference instances depending on the value of the

selector attribute. The set of Conferences could be

partitioned based on the Prestige attribute. In this

case P[Paper.Conference]={Prestige} and

Paper.Conference

Conference→{low,medium,high}.

ICEIS 2005 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

416

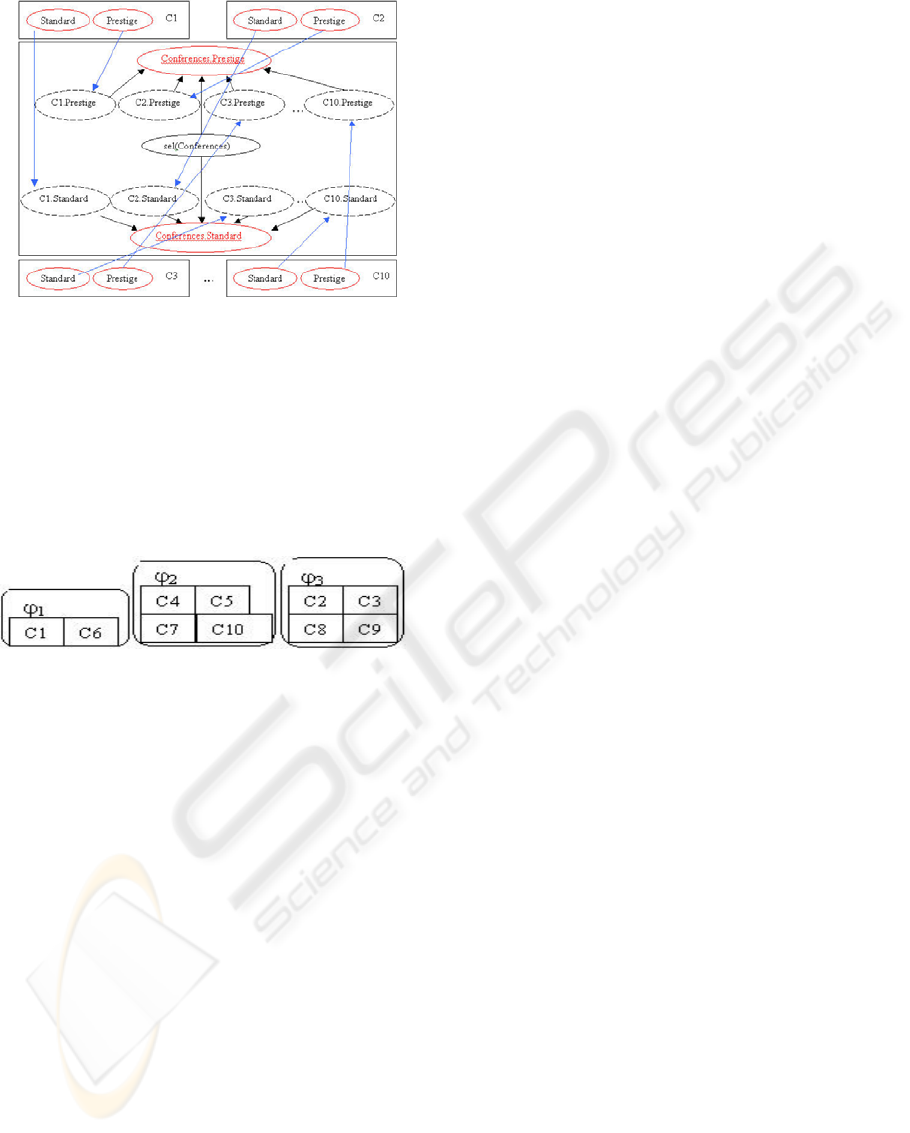
Figure 2: The equivalent BOOBN which would be used to

determine the values of Conference.Prestige and

Conference.Standard under reference uncertainty

The CPD for the selector attribute could be [0.1

0.6 0.3], i.e., it is 30% likely that the paper was

accepted by a prestigious conference, 60% likely the

paper was accepted by a conference with a medium

level prestige and 10% likely the paper was accepted

to a conference with a low prestige

Figure 3: An example of how the Conference instances

could be partitioned based on the Prestige of the

Conference where ϕ

is the set of conferences with low

prestige, ϕ

medium and ϕ

high

5.4 Existence Uncertainty

OPRM allow both real world objects and the

relationships between them can be represented by

classes. Existence uncertainty occurs when it is

uncertain whether a relationship exists between

objects. A set of potential relationship classes is

specified, but it is uncertain which relationships

actually exist. Existence uncertainty is required in

the competitive domains because there is often only

partial, indicative (not definitive) evidence of the

presence of a relationship between objects in the

market or battlespace. Existence uncertainty is

integrated into the probabilistic model of a class by

introducing an existence attribute.

Definition: An existence attribute is a

descriptive attribute whose value of {true, false}

depends on the existence attribute of all parents of

the existence attribute.

An existence attribute is represented in the

equivalent BOOBN by a simple node with links to

its parents. A class exhibiting existence uncertainty

is called undetermined and each instance of the class

contains an existence attribute. For classes that are

determined, the value of the existence attribute is

always true

6 FUTURE WORK

Like PRM, and indeed most current FOPL

approaches (Pasula 2003), OPRM employ the

unique names assumption. That is, each instance in

the knowledge base is assumed to correspond to a

different object. This assumption may be violated in

the military domain, where there is a distinct

possibility that multiple observations (and therefore

multiple instances in the knowledge base) may

represent the same object. In the military

information fusion domain, identity uncertainty

would have a profound impact on data association

(the tracking of objects from time to time and from

sensor to sensor). A recent thesis by (Pasula 2003)

investigated the incorporation of identity uncertainty

into PRM. Future work will include the

investigation of techniques for incorporating identity

uncertainty into OPRM.

The expressive power of OPRM makes it easy to

construct models whose equivalent OOBN will have

very large cliques. Incorporation of identity

uncertainty into the language would only exacerbate

this problem. We also intend to research and

implement appropriate approximate inference

algorithms

7 CONCLUSIONS

We have presented OPRM, a language that extends

the Object Oriented Bayesian Network framework

developed by Bangsø with a frame-based

representation. This language allows domains to be

modelled in a structured manner in terms of objects

and the relationships between them. We postulate

that once identity uncertainty is incorporated into the

language, OPRM will provide a flexible and

practical approach to reasoning in complex domains,

such as military or economic situation assessment,

where the unique names assumption cannot be

employed. We also postulate that the extended

version of OPRM will provide a formalism for the

Situation Assessment computational processes.

As relational databases are a common

mechanism for representing structured data (e.g.

medical records, sales and marketing information,

etc), OPRM are applicable to a wide range of

SITUATION ASSESSMENT WITH OBJECT ORIENTED PROBABILISTIC RELATIONAL MODELS

417

domains and applications for example, disaster

management and computer network security and

stock market modelling.

REFERENCES

Bangso, O. (2004). Object Oriented Bayesian Networks.

PhD Dept. of Computer Science, Aalborg University:

110.

Bangso, O., M. J. Flores, et al. (2004). Plug and Play

Object Oriented Bayesian Networks.

Bangso, O. and P.-H. Wuillemin (2000). Top Down

Construction and Repetitive Structures Representation

in Bayesian Networks. Proc. 13

FLAIRS, AAAI

Press.

Das, S., R. Grey, et al. (2002). Situation Assessment via

Bayesian Belief Networks. Proc. 5

Int'l Conf on

Information Fusion, Annapolis, MD, USA.

Flores, M. J., J. A. Gamez, et al. (2003). Incremental

Compilation of a Bayesian Network. Proc. 19

Conf

on Uncertainty in Artificial Intelligence, Morgan

Kaufmann.

Getoor, L. (2002). Learning Statistical Models From

Relational Data. PhD thesis Department of Computer

Science, Stanford University: 189.

Gonsalves, P., G. Rinkus, et al. (1999). A Hybrid Artificial

Intelligence Architecture for Battlefield Information

Fusion. Proc. 2

Int'l Conf on Information Fusion,

Sunnyvale, CA.

Gonsalves, P. G. and G. J. Rinkus (1998). Intelligent

Fusion and Asset Management Processor. 1998 IEEE

Information Technology Conference, Syracuse, NY.

Jones, P. M., C. C. Hayes, et al. (1998). CoRAVEN:

Modeling and Design of a Multimedia Intelligent

Infrastructure for Collaborative Intelligence Analysis.

Proc. of the IEEE Int'l Conf on Systems, Man, and

Cybernetics (SMC'98), San Diego, California.

Koller, D. and A. Pfeffer (1997). Object-Oriented

Bayesian Networks. Proc. 13

Conference on

Uncertainty in Artificial Intelligence, Providence, RI.

Koller, D. and A. Pfeffer (1998). Probabilistic Frame-

Based Systems. Proc. 15

National Conference on

Artificial Intelligence (AAAI-98), Madison,

Wisconsin.

Lambert, D. A. (2003). Grand Challenges of Information

Fusion. Proc. 6th Int'l Conf on Information Fusion,

Cairns.

Laskey, K. B. and S. M. Mahoney (1997). Network

Fragments: Representing Knowledge for Constructing

Probabilistic Models. Proc. 13

Conf on Uncertainty

in Artifical Intelligence, Providence, RI, Morgan

Kaufmann.

Llinas, J. (2001). Handbook of Multisensor Data Fusion.

Boca Raton, FL, CRC Press.

Mulgund, S., G. Rinkus, et al. (1997). OLIPSA: On-Line

Intelligent Processor for Situation Assessment. Proc.

Annual Symp on Situational Awareness in the

Tactical Air Environment, Patuxent River, MD.

Pasula, H. M. (2003). Identity Uncertainty PhD thesis in

Dept of Comp Sci, University of California, Berkeley.

Pfeffer, A., D. Koller, et al. (1999). SPOOK: A System for

Probabilistic Object Oriented Knowledge

Representation. Proc. 15th Conf Uncertainty in AI

(UAI-99).

Pfeffer, A. J. (1999). Probabilistic Reasoning for Complex

Systems.PhD thesis Dept of Comp Sci, Stanford Uni.

Salerno, J., M. Hinman, et al. (2003). Information Fusion

for Situational Awareness. Proc. 6th Int'l Conf on

Information Fusion, Cairns, Queensland.

Steinberg, A. N., C. L. Bowman, et al. (1998). Revisions

to the JDL Data Fusion Model. The Joint NATO/IRIS

Conference, Quebec, Canada.

Sycara, K. and M. Lewis (2002). From Data to Actionable

Knowledge and Decision. Proc. 5th Int'l Conf on

Information Fusion, Annapolis, MD, USA.

Wright, E., S. M. Mahoney, et al. (2002). Multi-Entity

Bayesian Networks for Situation Assessment. Proc.5

Int'l Conf on Information Fusion.

ICEIS 2005 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

418