OBJECT ID DISTRIBUTION AND ENCODING IN THE

SEMANTIC BINARY ENGINE

Naphtali Rishe, Armando Barreto, Maxim Chekmasov,

Dmitry Vasilevsky, Scott Graham, Sonal Sood

Florida International University, Miami, FL

Ouri Wolfson

University of Illinois at Chicago, Chicago, IL,

Keywords: Semantic binary data model, object id encoding/decoding, clustered id distribution

Abstract: The semantic binary engine is a database management system built on the principles of the Semantic Binary

Data Model (Rishe, 1992). A semantic binary database is a set of facts about objects. Objects belong to

categories, are connected by relations, and may have attributes. The concept of an object is at the core of the

data model and it is crucial to have efficient algorithms that allow the semantic binary engine to store,

retrieve, modify and delete information about objects in the semantic database. In this paper, we discuss the

concept of object IDs for object identification and methods for object ID distribution and encoding in the

database. Several encoding schemes and their respective efficiencies are discussed: Truncated Identical

encoding, End Flag encoding, and Length First encoding.

1 INTRODUCTION

The semantic binary engine stores information about

the database schema and abstract objects as a set of

facts at the logical level (Rishe, 1992). At the

physical implementation level, every fact is encoded

as a binary string using a reversible encoding. The

abstract objects, the categories they belong to, and

the relations and inverse relations between objects

are all assigned object IDs for their proper

identification. This makes the concept of object ID,

and the mechanisms related to their generation,

deletion, assignment, encoding, and storage, an

important part of the database engine.

One question that should be answered for the

plementation of the semantic binary engine is

whether to have object IDs of a fixed-size, a

flexible-but-limited-size, or a flexible-unlimited-

size. With fixed-size object IDs, a predefined

number of bits is used to identify every object in the

database. This number stays the same whenever the

object ID is stored on disk or used in memory. This

means that only a limited number of objects can be

identified by an object ID and that we should choose

the size of object ID to be large enough to cover a

reasonable number of objects present in real world

applications. Object IDs of a flexible-but-limited-

size would allow us to have shorter IDs in small

databases as long as the number of IDs is also

limited for the database. With a flexible-but-limited-

size approach, the object IDs that are stored on disk

have a variable size, while the object IDs in memory

are decoded to the maximum size to ease

computation. In the flexible-unlimited-size

approach, the number of objects in the database is

potentially unlimited; object IDs of the same size are

used on disk and in memory.

Flexible-unlimited-size IDs allow for the storage

of a l

arge, and potentially unlimited, amount of data,

but require complex coding and higher overhead to

support the flexible ID size. There are also

limitations imposed by the database engine structure

which deny efficient support for the database

growing in size beyond original assumptions. IDs of

database schema objects are used in almost every

fact stored in the database; therefore it is beneficial

to keep them short. The use of flexible-but-limited-

size object IDs seems to be the most reasonable

approach.

There are many algorithms for object ID

gene

ration. IDs can be generated sequentially for

every allocated object. Another approach is to

generate random IDs, where the objects are

279

Rishe N., Barreto A., Chekmasov M., Vasilevsky D., Graham S., Sood S. and Wolfson O. (2005).

OBJECT ID DISTRIBUTION AND ENCODING IN THE SEMANTIC BINARY ENGINE.

In Proceedings of the Seventh International Conference on Enterprise Information Systems, pages 279-284

DOI: 10.5220/0002535702790284

 SciTePress

distributed randomly across the ID space. Finally,

IDs can be allocated in clusters. This last approach

improves the performance of several database

algorithms as discussed below.

2 ENCODING OF OBJECT IDS

Object IDs are used to identify objects by the

database engine. If objects are composed of

relatively small-size attributes like integers or

Boolean values, keeping an object ID for every fact

introduces a noticeable space overhead in

comparison to similar relational databases. The

database engine spends most of its processing time

for operations with object IDs; for example,

comparisons of object IDs are made quite

frequently. Thus, the task of finding an efficient

object ID encoding scheme is a challenge which

needs to be carefully pursued by the database engine

designers.

Encoding of object IDs is a reversible function

φ:[0..N]→{α|α - binary string, |α|< m}

where N is integer and [0..N] is the space covered

by encoding. φ([0..N]) is the encoded space. The

function should be defined for every number in the

interval [0..N] and should result in different

values for all the interval numbers to ensure the

existence of an inverse function φ

-1

, which makes

encoding non-destructive. The encoded space does

not have to cover the entire {α|α - binary string,

|α|< m}.

To be a valid encoding function, φ should satisfy

the following conditions.

(1) ∀a,b∈[0..N], a< b ⇒ φ(a)< φ(b)

The encoding function should preserve order. If

the number is smaller than another number,

encoding should yield the same lexicographical

order. This condition is required since object ID

comparisons by the engine are performed on original

as well as encoded object IDs. The comparisons

should yield the same result.

(2) ∀a,b∈[0..N], φ(a)< φ(b),

∀α,β-string ⇒ φ(a)⋅α< φ(b)⋅β

No matter what is appended to the encoded

string, the resulting string should preserve

lexicographical order. Though conditions (1) and (2)

can be stated as one condition, we feel that it is

clearer to state them separately. Condition (2)

guarantees the correct retrieval of facts regarding a

certain object. The facts that start with the same

object ID form a continuous interval with respect to

lexicographical order. No fact about another object

can be encoded between them.

(3) ∀a,b∈[0..N], if ∃ α,β - string so that

φ(a)⋅α = φ(b)⋅β ⇒ a = b

If the object ID is concatenated with a string, it

should still be extractable from the resulting string.

Condition (3) is needed since encoded facts are

constructed by appending strings to encoded object

IDs. In many cases object IDs need to be extracted

from already encoded facts.

2.1 Truncated Identical Encoding

To illustrate a situation where condition (3) is

violated, let us consider the following encoding. An

object ID is formed byte-by-byte. The first byte is

the most significant non-zero byte of the number,

then other bytes follow in order. We call this method

truncated identical encoding and denote its function

as ε.

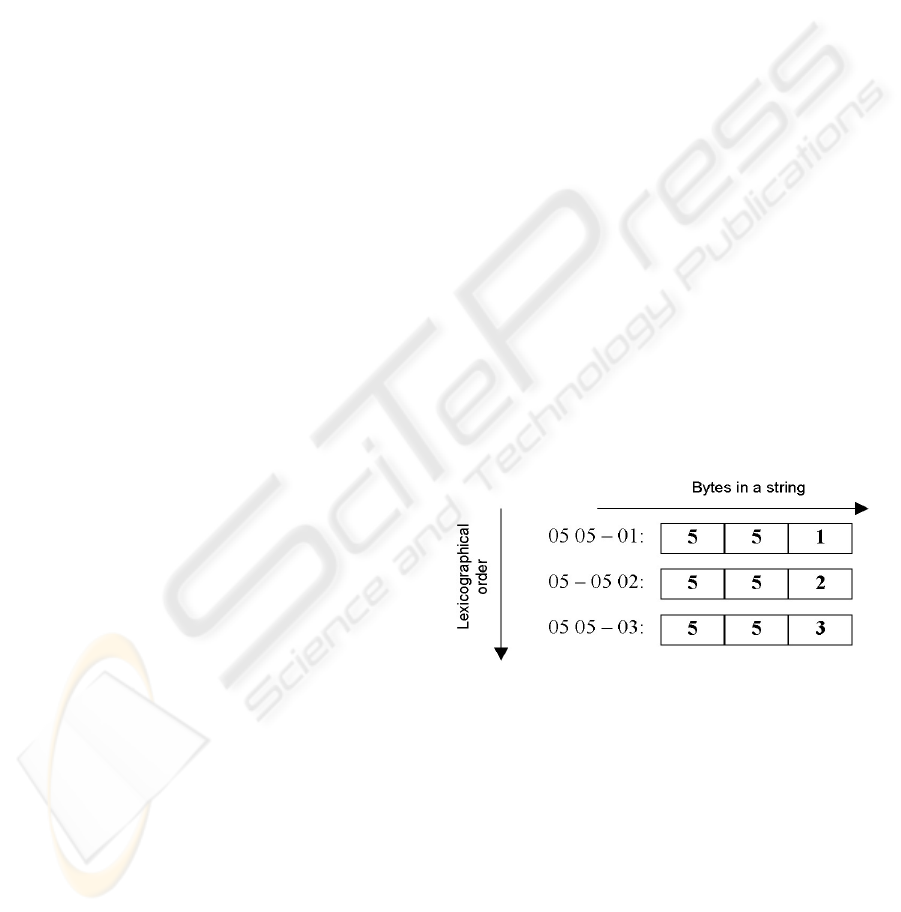
As shown on Figure 1, when bytes 0x05 0x02

are appended to encoded ID 0x05 in line number 2,

it causes the resulting string to be lexicographically

between two strings for the object ID 0x0505.

Though truncated identical encoding violates all

three conditions above, it is still used for different

purposes.

Figure 1: Lexicographical order example

Condition (1) on φ guarantees that the B-Tree

lexicographical order used to index facts is the same

as the natural ordering of integer numbers. If

condition (1) were relaxed, all comparisons should

be performed on either encoded strings or un-

encoded numbers. Since the B-Tree utilizes

comparisons on encoded strings, all the comparisons

would have to be done this way. However, that

would causes a problem and overcomplicate the

database engine design, since the object ID-

allocating algorithm and the bit-scale storage

ICEIS 2005 - DATABASES AND INFORMATION SYSTEMS INTEGRATION

280

scheme both make use ordering of un-encoded

numbers.

When conditions (1)-(3) are met, one has a valid

encoding function. However, the encoding could be

inefficient. Consider the trivial encoding of

[0..2

], which utilizes exactly n-byte strings to

represent the number. The string is composed of all

the bytes starting from the most significant bytes

even if they are 0 bytes. This is called identical

encoding. It satisfies the three required conditions,

but it is not efficient in terms of space. With n=2,

large databases are not covered. With n=8, there is

a great deal of wasted space on long object IDs in

small databases. For example, ID=0x21 will be

encoded as 0000000000000021. We can not

truncate leading zero bytes since the resulting

encoding would not satisfy the required conditions.

The choice of encoding function along with the

object ID size plays a major role in achieving a

successful semantic binary engine design. It is also

important to determine the space requirements for

object IDs and the way object IDs are generated and

disposed of. Existing ID encoding conventions

might be utilized. An example encoding technique is

Globally Unique Identifiers (GUIDs), where each

object ID is a 16-byte integer and an algorithm is

available for generating GUIDs, as is the procedure

for discarding GUIDs when objects are disposed.

2.2 Efficiency of Encoding

The following properties are desirable features of an

efficient object ID system for the semantic binary

engine.

(I) Encoded object IDs should be short for small

numbers. For a database with several thousand

objects, a maximum object ID that is 8 bytes long

would be considered a waste of space. More

importantly, even large databases usually have

relatively small schemas. A category ID or relation

ID is present in every fact in the database. Therefore,

if all relations and categories in the schema have

short encoded object IDs, the overhead for storing

them would be low.

(II) The space of object IDs should cover large

datasets. It is possible to design a system with

unlimited-size object IDs, but the system would be

excessively complex and inefficient. Given a limit

on the length of encoded strings, the space of object

IDs should be as large as possible. If the length of

encoded strings is limited to n bytes, the space of the

maximum possible size covered by object IDs is 2

objects, achieved by identical encoding.

(III) The encoding (φ) and decoding (φ

-1

)

algorithms should not be computationally complex.

Though it is hard to beat the speed of identical

encoding, which could likely be implemented as a

single CPU instruction, the encoding algorithm

should come as close as possible.

(IV) ε

-1

(φ()) should preserve ordering and

-1

(φ([0..N])) should be dense—preferably

containing only a few interval holes. This is similar

to treating encoded strings as numbers without

decoding. As an illustration, consider the following

approach. While the encoding/decoding function is

conventionally run every time an object ID is stored

or retrieved from a fact, it is possible to avoid this.

Most of the engine operations can be performed on

encoded IDs. One can apply ε

-1

to encoded object

IDs, making a number out of it without decoding;

more accurately ε

-1

•φ:[0..N]→[0..M]. The

function ε

-1

is fast and, by (IV), the ordering is

preserved. After applying fast encoding ε to the

resulting numbers, the original coded strings can be

obtained.

If property (IV) is satisfied, we can use

-1

(φ([0..N])) = Φ ⊂ [0..M] inside the engine as

object IDs. This would save time by eliminating

encoding and decoding in most operations.

However, in this case, it is desirable that this set is

dense in [0..M] since the database engine uses

bitmaps for efficient indexes on attributes that have

only few possible values such as Boolean attributes

or the flag of belonging to a category. If Φ is not

dense enough, space in a bitmap is wasted for non-

existent object IDs.

Actually, Φ might have structure rather than just

being dense. As an illustration, consider the

compression of bitmaps used in the engine. Bitmaps

are broken into blocks; if a whole block contains

only zeroes, it is compressed out. This is a simple

and fast compression. Typically, a block of object

IDs is given to a category and new objects in that

category get IDs from the block. This ensures that

compression of the bitmaps works well since almost

every set consists of objects from the same category.

(V) It is not desirable to have different encoding

for databases of different space sizes. If N

< N

, φ

is the encoding for [0..N

] and φ

is a version of

the same encoding for [0..N

], then ∀x<N

⇒

(x)= φ

(x). This ensures that if the ID space

expands over time, the database would remain

compatible. Properties (I) and (II) provide an

alternative solution for functions that do not satisfy

(V). If the ID space is chosen large enough from the

very beginning, small databases would have short

IDs and therefore there will be no waste in terms of

database space.

An ID space of 2

covers all currently existing

databases and the databases of the foreseeable

future. Let us review encodings we’ve discussed so

far and see if they satisfy the three requirements and

have the five properties discussed above.

OBJECT ID DISTRIBUTION AND ENCODING IN THE SEMANTIC BINARY ENGINE

281

Identical encoding trivially satisfies the three

properties and therefore is a valid encoding. It has to

use n=7 to cover the required space. Identical

encoding is an efficient encoding function—the

most efficient of all possible encodings. The

problem with identical encoding is that it does not

satisfy property (I). Small databases would have to

use long object IDs, this encoding does not satisfy

property (V) either.

Truncated identical encoding satisfies property (I)

since it uses a minimum amount of bytes to encode a

number. It satisfies (II), since this encoding can use

as many bytes as needed and covers the maximum

possible space. Truncated identical encoding

satisfies (III), since a “would be” encoding and

decoding algorithm is very simple with few CPU

instructions involved. It satisfies (IV) and produces

the densest set possible, which is the whole interval.

It also satisfies (V). However it violates all three

conditions and, therefore, is not a valid encoding.

A reasonable, practical, solution seems to be found

somewhere between these two encoding methods.

2.3 End Flag Encoding

End Flag starts with the 7 least significant bits of the

number, which are used as the 7 least significant bits

of the last byte of the encoded string. The most

significant bit is set to 0. Then 7 more bits from the

number are taken to form the last-but-one byte of the

encoded string. The most significant bit is set to 1.

The process continues while there are non-zero bits

in the original number taking 7 bits at a time and

adding 1 as the most significant bit to the resulting

byte. The last byte formed will be the first byte of

the resulting encoded string.

End Flag encoding satisfies all three conditions of

valid encoding. Indeed, one can always find the end

of the number since only the last byte has the highest

bit set to 0, therefore (3) is satisfied. The same

consideration is valid for (2). Requirement (1) is

satisfied since the longer the number the greater the

encoded string; the most significant bit indicates

that.

With respect to the set of properties for efficient

encoding, (I) is satisfied. For objects IDs from

[0..2

-1], the length of an encoded object ID is

only one byte. For objects from [2

..2

-1] it is

two bytes, etc. Property (II) is also valid with this

encoding. For the required ID space of 2

objects,

the maximum length of a string is 8 bytes. Property

(III) is satisfied only to a certain extent. Even though

the algorithm is faster than the original encoding,

proposed in (Rishe, 1991), it is still about fifty times

slower than identical encoding (one CPU

instruction). It is questionable whether property (IV)

is met, since there are many interval holes in Φ,

namely a hole of 128 numbers every 256 numbers

and even more holes for higher powers of 2.

Property (V) is satisfied since ID space has room to

grow beyond the original expectations.

2.4 Length First Encoding

Length First covers a space of 2

objects. The three

most significant bits of the first byte of the encoded

string contain the string’s length-1. All other bits

are copied from the number. The algorithm is as

follows. Start with the least significant bit of the

number and copy it to the least significant bit of the

last byte of the resulting string. Continue copying bit

by bit until reaching the most significant non-zero

bit of the number. If the current byte of the encoded

string still has three highest bits unassigned, set them

to the length of the encoded string-1, otherwise add

another byte at the beginning and set the highest

three bits to the length of the encoded string-1.

Length First encoding satisfies the three

conditions of valid encoding. The length of encoded

string can easily be found, since it is stored in the

three most significant bits of the first byte. Similarly,

(2) is satisfied. Requirement (1) is also satisfied,

since longer numbers mean larger numbers and the

length is represented by the three most significant

bits of the encoded string. For numbers of the same

length, conventional comparison rules apply.

With respect to the set of properties for efficient

encoding, property (I) is satisfied. For object IDs

from [0..2

-1], the length of the encoded string

is one byte. For [2

..2

], the length is two bytes.

This is less efficient than End Flag encoding for

short IDs, but is better for longer IDs. Property (II)

is satisfied. For the ID space of [0..2

], the

maximum length of an encoded string is eight; this is

better than in the End Flag algorithm. Property (III)

is satisfied and Length First encoding is faster than

the End Flag encoding; since the encoded string’s

length is given in the first three bits, it is only about

ten times slower than identical encoding. Property

(IV) is satisfied; for the considered space, Φ has

only 7 interval holes. Property (V) is not satisfied,

which means that the space of object IDs should be

chosen at the engine design phase and can’t be

extended. However, the space of [0..2

] is larger

than required for most database applications.

2.5 Mapped Length First Encoding

Mapped Length First encoding is a modification of

the Length First algorithm. Instead of using three

bits for length encoding it uses only two bits. The

four possible bit combinations are mapped to string

ICEIS 2005 - DATABASES AND INFORMATION SYSTEMS INTEGRATION

282

lengths according to Table 1. Figure 2 illustrates the

number of object IDs available with the different

Mapped Length First bit combinations.

Table 1: Length mapping for Mapped Length First ID

encoding

Bit combination ID Length

00 1 byte

01 2 bytes

10 4 bytes

11 8 bytes

Figure 2: Mapped Length First object ID space

Let us prove that Mapped Length First encoding is a

valid encoding.

Consider N

. If |φ(N

)|=|φ(N

)|, it is

evident that φ(N

)>φ(N

). Indeed, the two most

significant bits of φ(N

) are equal to two most

significant bits of φ(N

), therefore the result of a

comparison is determined by the remaining bits. The

remaining bits are compared in the same way as the

original numbers. If they are of different length,

|φ(N

)|>|φ(N

)|, by construction, since the two

most significant bits of φ(N

) are greater than two

most significant bits of φ(N

). Therefore

φ(N

)>φ(N

Consider φ(N

)>φ(N

). If the two most

significant bits of φ(N

) are greater than the two

most significant bits of φ(N

) then it does not

matter what is appended after these bits. If the two

most significant bits of φ(N

) are the same as the

two most significant bits of φ(N

) then

|φ(N

)|=|φ(N

)|. Therefore it does not matter

what is appended after two most significant bits

since φ(N

)>φ(N

If φ(a)⋅α=φ(b)⋅β, then the first two significant

bits of φ(a) are the same as two most significant

bits of φ(b). This means |φ(a)|=|φ(b)|.

Therefore φ(a)=φ(b).

Now, let us consider the efficiency of this

encoding. All numbers from the interval [0..2

1] take one byte to be encoded, the numbers from

the interval [2

..2

-1] take two bytes to be

encoded. Numbers from the interval [2

..2

-1]

take four bytes to be encoded.

This encoding covers in total the interval

[0..2

], which is actually more than required for

most database applications.

The encoding is fast. It is only about ten times

slower than identical encoding.

Φ defined by this encoding has only three interval

holes.

Property (V) is not satisfied. However, this is

mitigated by having short object IDs for small

numbers and large enough space for object IDs.

Length First and Mapped Length First algorithms

are similar, except that the latter improves space

consumption for small IDs by sacrificing space

consumption for medium IDs. This is helpful for

small databases with small database schemas.

Mapped Length First is an efficient encoding which

can be implemented with at most ten Intel assembly

instructions.

One more approach is to make the database

engine choose the encoding algorithm dynamically

(Vasilevsky, 2004). In turn, this means that object

IDs encoded by different algorithms might coexist in

the same database and that the database engine

should choose the correct algorithm for decoding

any given object ID. Thus, an allocation of space in

the encoded object ID is needed to indicate which

decoding algorithm to use. For example, another

algorithm can be used to encode large object IDs in

Mapped Length Encoding. The first two bits being

equal to 11 would be an indication of the use of this

algorithm. However, the overall encoding that

results from dynamically choosing among the

different algorithms should satisfy all encoding

properties.

3 GENERATION AND DISPOSAL

OF OBJECT IDS

We propose to enhance the basic algorithms for

object ID generation to allow the database engine to

better store and manipulate object IDs. The

enhancement is described as follows.

A request for a new object ID should not go

directly to the central generator of object IDs.

Instead, the central ID generator should give every

category a continuous set of IDs that fall into one

block of a bitmap. Then, whenever an object is

created in the category, it receives an object ID from

the block allocated for that category. When the block

is exhausted, the category requests another one from

the central ID generator.

This approach allows bitmaps storing object

categorization to be very compact. Suppose that

OBJECT ID DISTRIBUTION AND ENCODING IN THE SEMANTIC BINARY ENGINE

283

every object belongs to exactly one category and

never migrates across categories. In this case, we

find the bitmaps that represent categorization

information in an ideal situation. For category C, the

blocks of object IDs that were allocated to the

categories other than C will always have only zeros

and thus will not be stored after applying our bitmap

compression scheme. Blocks of object IDs that were

given to category C will all have ones (except,

perhaps, the last block) and will not be stored either;

see Figure 3. This method takes advantage of the

fact that objects rarely change their category. Thus a

set of objects belonging to one category would most

likely form several intervals with dense object ID

distribution. The set can be represented very

efficiently by a bit scale.

Figure 3: Clustered object ID distribution

When the central ID generator is requested to

provide a new set of object IDs, it increases the

value of the global counter and applies the function

-1

(φ()) to it. No additional computing is required

for previously generated object IDs. In other words,

after initial generation of object IDs for the database,

an efficient function ε for encoding is utilized but

the domain space of IDs is restricted to this initial ID

set.

Each repository of a category’s object IDs uses

bit scale storage. Whenever an object is disposed, its

object ID is returned to the repository of the

corresponding category. Whenever the repository

detects that an entire block of object IDs is free, it

returns the block to the global repository of object

IDs.

The size of the database can be optimized by

carefully choosing object IDs for objects in the

database schema. Every fact in the database has one

object ID from the database schema. Therefore, it is

beneficial to use short object IDs for the objects in

the database schema. The semantic database engine

employs predefined object IDs for the objects in the

metaschema. The predefined object IDs should be

excluded from the ID allocation algorithm. If short

objects IDs are used for the metaschema objects,

they can no longer be used for objects in the

database. Therefore, predefined objects in the

metaschema should not be taken from the beginning

of the object ID space; they should be taken from the

end of ID space. This keeps the object allocation

algorithm simple and allows short object IDs to be

used for new objects in the database schema.

4 CONCLUSION

Choosing methods for object ID encoding and

distribution is crucial for the design of a fast and

reliable semantic binary database engine. For

efficient encoding of object IDs, we propose to

allocate the most significant bits in an object ID as

storage to encode length of an ID and to use the

remaining bits to store the integer value of an ID

directly. For practical purposes, it is recommended

to use one-, two-, four-, and eight-byte encoded IDs

for database objects, while short one- and two-byte

IDs should be chosen for the database schema

objects, since these IDs are present in every fact

stored in the database.

With respect to object ID generation, we propose

to generate object IDs in blocks. The blocks of IDs

are assigned to the categories, thus a new object to

be stored in the database receives an object ID from

its category repository. This clustered ID distribution

provides an effective storage and data retrieval

solution, though it should be combined with other

methods when the objects are allowed to change

categories.

ACKNOWLEDGEMENTS

This material is based on work supported by the

National Science Foundation under Grants No.

HRD-0317692, EIA-0320956, EIA-0220562, CNS-

0426125, IIS-0326284, CCF-0330342, IIS-0086144,

and IIS-0209190.

REFERENCES

Rishe, N., 1992. Database Design: the Semantic Modeling

Approach, McGraw-Hill. 528 pp.

Rishe, N., 1991. Interval-based approach to lexicographic

representation and compression of numeric data. Data

& Knowledge Engineering, n 8, pp. 339-351.

Vasilevsky, D., 2004. Design Principles of Semantic

Binary Database Management Systems, PhD thesis,

Florida International University, 165 p.

ICEIS 2005 - DATABASES AND INFORMATION SYSTEMS INTEGRATION

284