
CONDITIONS FOR INTEROPERABILITY
Nick Rossiter
School of Informatics, Northumbria University, NE1 8ST, UK
Michael Heather
Northumbria University, NE1 8ST, UK
Keywords:
semantic interoperability, organisational interoperability, Godement calculus, commuting diagrams.
Abstract:
Interoperability for information systems remains a challenge both at the semantic and organisational levels.
The original three-level architecture for local databases needs to be replaced by a categorical four-level one
based on concepts, constructions, schema types and data together with the mappings between them. Such
an architecture provides natural closure as further levels are superfluous even in a global environment. The
architecture is traversed by means of the Godement calculus: arrows may be composed at any level as well as
across levles. The necessary and sufficient conditions for interoperability are satisfied by composable (formal)
diagrams both for intension and extension in categories that are cartesian closed and locally cartesian closed.
Methods like partial categories and sketches in schema design can benefit from Freyd’s punctured diagrams to
identify precisely type-forcing natural transformations. Closure is better achieved in standard full categories.
Global interoperability of extension can be achieved through semantic annotation but only if applied at run
time.
1 CLASSICAL DATA
STRUCTURES
Classical information systems employ some suitable
model to mediate between data and hardware. A data-
base model is a representation of policies in a struc-
tured form according to some perceived view of real-
ity.
In the ANSI/SPARC architecture (Tsichritzis,
1978) a conceptual schema or model is defined as a
global logical definition of the data structure. This
schema relates to the internal (physical) definition by
a mapping from the logical level to the physical level.
The schema is protected from changes at the physical
level by adjusting this mapping. Each user has a par-
ticular view (external schema) of the database which
may be a restricted view. The architecture including
the series of mappings shown in Figure 1 provides as-
pects such as security and logical data independence.
The classical ANSI/SPARC architecture of Figure
1 has the disadvantage that the levels are not indepen-
dent of each other. This may be compared with the
natural architecture of Figure 2 (Heather and Rossiter,
Internal schema I
Conceptual schema C
External schema E
6
6
?
?
Figure 1: Classical ANSI/SPARC Architecture for Data-
bases
2002). The four levels (top-down) are categories for
concepts (real-world abstractions), constructs (facili-
ties available for schema design), schema (definition
of data types available in system) and data (the data
itself). In ANSI/SPARC the types of the three lev-
els are similar to the external schema but the internal
schema is composed of subcategories of the concep-
tual schema. The top level, the external schema, is
not a universal closure of types but a local closure
of the conceptual schema. The four-level architec-
ture in Figure 2 has orthogonal types with the rela-
92
Rossiter N. and Heather M. (2005).
CONDITIONS FOR INTEROPERABILITY.
In Proceedings of the Seventh International Conference on Enterprise Information Systems, pages 92-99
DOI: 10.5220/0002530200920099
Copyright
c
SciTePress
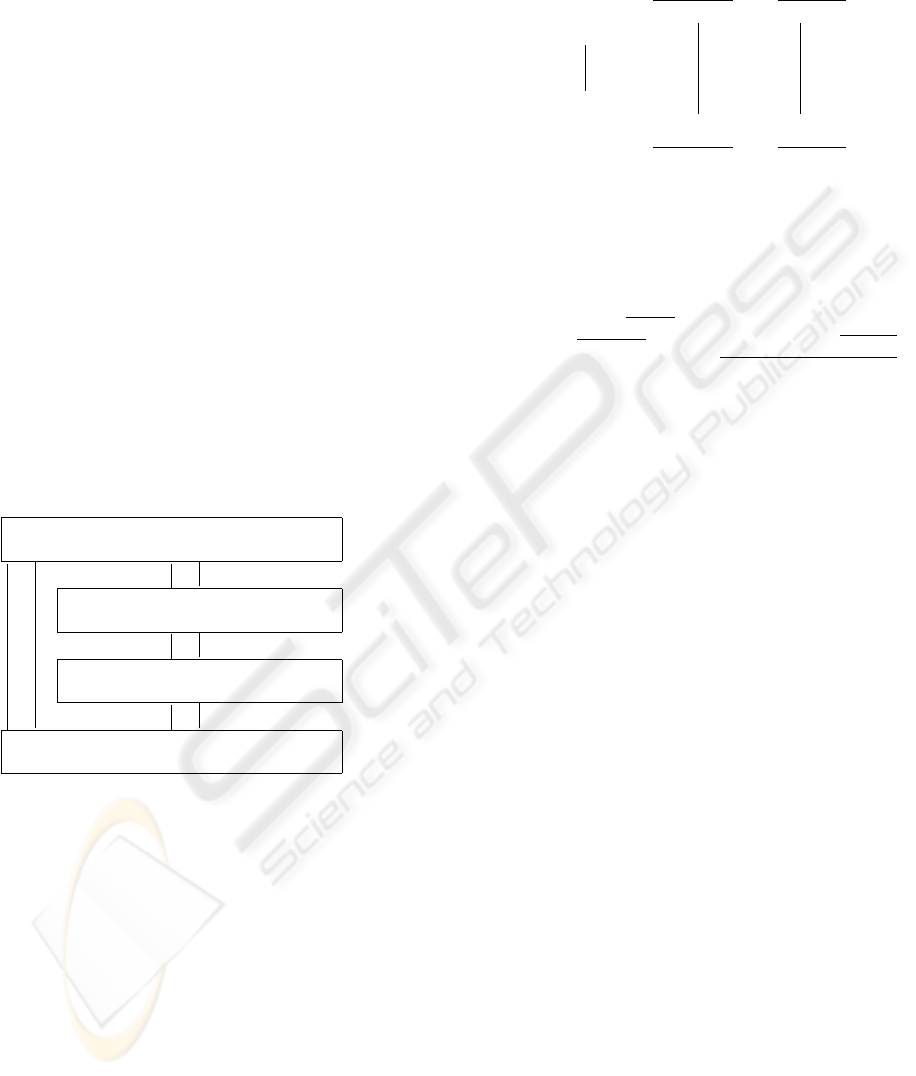
tionships between the levels expressed as categorical
adjunctions as already applied to structures in GRID
data processing (Heather and Rossiter, 2002). Cate-
gorical adjunctions relate one level to another. The
relationship between levels is measurable by the unit
of adjunction. For instance the adjunction P olicy ⊣
MetaMeta indicates that the free functor P olicy
is left adjoint to the underlying functor M etaM eta.
The unit of adjunction is given by η
cpt
: 1
cpt
−→
MetaMeta ◦ P olicy(cpt).
The ANSI/SPARC architecture was a useful way of
capturing abstractions of the relational model in the
1970s and 1980s. It has proved less suitable to facil-
itate the techniques needed today such as interoper-
ability where systems with different underlying mod-
els are required to work together. ANSI/SPARC can
be viewed as pseudo-natural. It was developed using
mathematical techniques and theories like sets. But
there is a gap between classical theory and real-world
performance and pragmatics. Triggers are an example
of an attempt to patch the weakness of the system by
providing some local strong anticipation using Event-
Conditions-Actions (ECA) (Date and Darwen, 2000).
Concepts
P olicy ⊣ MetaMeta
Constructs
O rg ⊣ Meta
Schema
Data
Instance ⊣ Classif y
Instance
mission
management
enterprise
information
execution
application
?
6
MetaMeta Policy
?
6
Meta
Org
?
6
Classify
?
6
Sys
Platform
Figure 2: Interpretation of Levels: natural schema with
strong anticipation
In Figure 2 the terms used have their normal mean-
ing. Basically in the downward direction, a collec-
tion of data structuring concepts (abstractions) are
mapped through policies to a collection of construc-
tions (for example classes, tables) which are in turn
mapped through organisation to a collection of types
(for example, schema definitions) which are finally
mapped through instantiation to named data values.
In the opposite direction, the named data values are
mapped through classification to types, which are in
turn mapped through metadata to constructions which
are finally mapped to concepts through metameta
data.
1.1 Natural Closure
CPT
CST SCH DAT
P
O I
P
′
O
′
I
′
CST
′
SCH
′
DAT
′
α
β γ
*
- -
H
H
H
H
Hj
- -
?
? ?
Figure 3: Comparison of Mappings in two Systems
In category theory four levels are needed to define
an arrow as unique up to natural isomorphism. The
four levels are: 1) object or identity arrow (within a
category), 2) category
(comparing objects), 3) functor
(comparing categories) and 4) natural transformation
(comparing functors). No more levels are required.
The relationships between one four-level architec-
ture and another can be constructed as in Figure 3, the
expanded view of Figure 2. Here for simplicity the
mappings are viewed in one direction only. Two sys-
tems are compared, one involving categories CPT,
CST, SCH and DAT, the other CPT, CST
′
,
SCH
′
and DAT
′
, representing concepts (CPT),
constructs (CST), schema (SCH) and data (DAT)
from Figure 2. CPT is the same in both systems as
there is one universal type for concepts. As usual the
functors relate the categories. We have now though
added natural transformations to relate the mapping
between one functor and another. It needs to be em-
phasised that none of these categories are discrete: all
have an internal arrow-based structure so the natural
transformations are non-trivial (Rossiter, 2003). The
functors need to be of the same variance for a mean-
ingful natural transformation to exist between them
and this is the case for α, β and γ.
An arrow comparing natural transformations is it-
self a natural transformation. Some categorists use
an older terminology with degrees of ‘cell’ and de-
scribe the identity arrow as 0-cell, an arrow in a cate-
gory as 1-cell and an arrow between arrows as a 2-cell
(Kelly and Street, 1974). An arrow from one natural
transformation to another gives a composition of the
natural transformations, not a new level (((Barr and
Wells, 1999), 1st ed., at p.85); (Rossiter and Heather,
2003)). This means that four levels are needed to give
the natural closure (Heather and Rossiter, 2002).
An alternative view to Figure 3, shown in Figure
4, is closer to the four levels inherent in category the-
ory. The fundamental levels are considered to be data
values, named values, classified values and contrasted
representation corresponding in category theory to
object, category, functor and natural transformation
respectively. The natural transformations are now the
CONDITIONS FOR INTEROPERABILITY
93
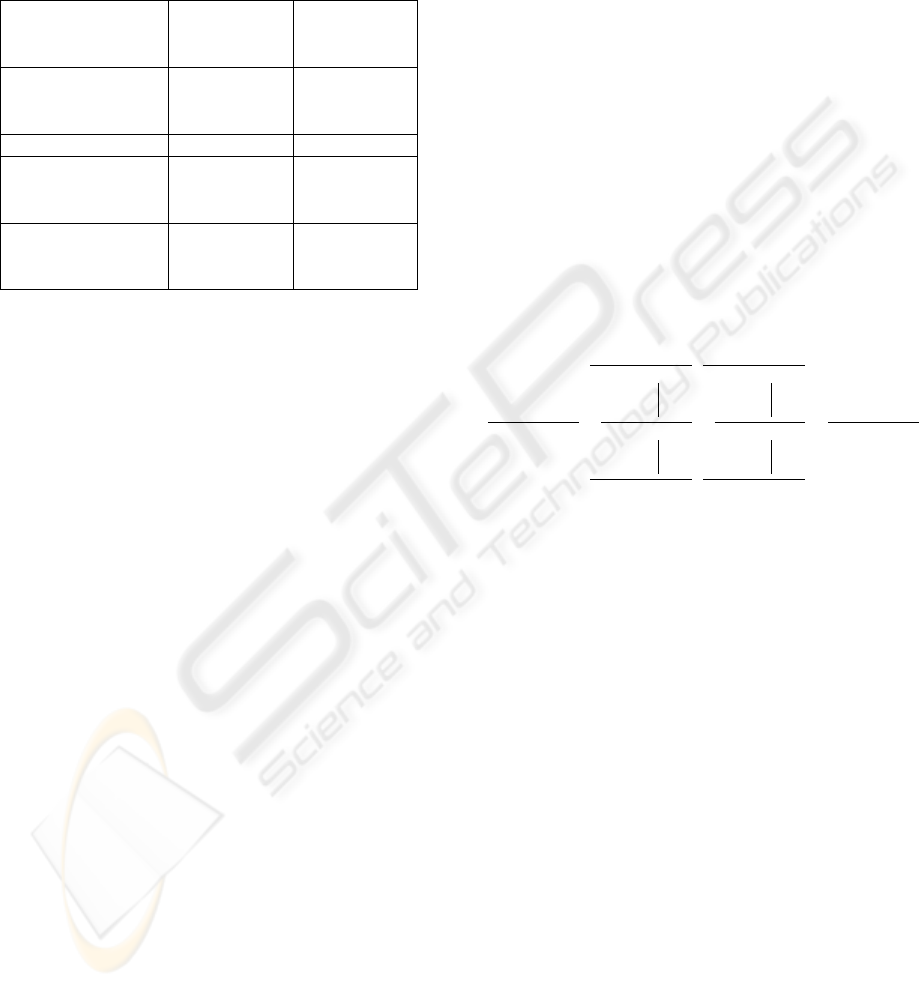
duals of those shown earlier in Figure 3 as indicated
by the op superscript. The earlier natural transforma-
tions were comparing the downward functorial map-
ping (towards data) while the current ones compare
the upward mapping (away from data) (Rossiter and
Heather, 2003).
alternative funda-
mental levels
category
theory
levels
four levels
of Figure 2
1. data values objects
(identity
arrows)
id
dat
2. named values category DAT
3. classified val-
ues
functor I
op
:
DAT −→
SCH
4. contrasted rep-
resentation
natural
transforma-
tion
α
op
◦ β
op
Figure 4: Alternative Interpretation of Levels in the Archi-
tecture
It can be shown (Rossiter and Heather, 2003) that
the addition of further levels is possible but nothing
is gained by it type-wise. Thus addition of an ex-
tra level to the top of a four-level architecture sim-
ply results in the top level (comparison of mapping
from concepts to schema) being a composition of
three arrows rather than two. Thus consider the ad-
dition of a new top level PHI with the mappings
F : PHI −→ CPT, G : CPT −→ PHI and
α
op′
: F −→ F
′
where α
op′
compares the mappings
F and F
′
in two different approaches. The adjunction
is now I ◦ O ◦ P ◦ F ⊣ G ◦ A ◦ M ◦ C. The level
four of Figure 4 is now α
op′
◦ α
op
◦ β
op
and is still
a natural transformation through the rules of compo-
sition. The practical consequence is that a fifth level
is equivalent to an alternative fourth level. The meta-
meta level gives ultimate closure of types.
2 NATURAL CALCULUS
We therefore have three types of mapping to con-
sider: within a category (for instance from a name to a
value), from one category to another (for instance the
functor P
′
from CPT to CST
′
) and from one func-
tor to another (for instance the natural transformation
α from P to P
′
).
Following the constructive principles of category
theory, the composition of these arrows is natural.
This consequently gives rise to a natural calculus
first expounded by (Godement, 1958) and ((Barr and
Wells, 1999), 1st ed., pp 94-97) in the form of rules
governing composition. The composition of functors
and natural transformations is associative so that for
instance in Figure 3:
(I
′
O
′
)α = I
′
(O
′
α); γ(OP ) = (γO)P
Natural transformations may be composed with
each other:
γβ = (γO ) ◦ (I
′
β); βα = (βP ) ◦ (O
′
α)
Godement’s five rules are given by ((Barr and
Wells, 1999), 1st ed., p.96-97).
Consider as in Figure 5:
five categories A, B, C, D and E
the following eight functors:
E : A −→ B, F
1
, F
2
, F
3
: B −→ C, G
1
, G
2
, G
3
:
C −→ D, H : D −→ E
and the following four natural transformations:
α : F
1
−→ F
2
, β : F
2
−→ F
3
, γ : G
1
−→ G
2
,
δ : G
2
−→ G
3
,
A B C D E
E F
2
G
2
α γ
H
F
3
β
G
3
δ
F
1
G
1
- - - -
- -
- -
? ?
? ?
Figure 5: Godement in (Barr and Wells, 1999), 1st ed., p.96
Then the following rules hold:
(δ ◦ γ)(β ◦ α) = (δβ) ◦ (γα) (1)
(H ◦ G
1
)α = H(G
1
α) (2)
γ(F
1
◦ E) = (γF
1
)E (3)
G
1
(β ◦ α)E = (G
1
βE) ◦ (G
1
αE) (4)
γα = (γF
2
) ◦ (G
1
α) = (G
2
α) ◦ (γF
1
) (5)
Equation 5 is particularly interesting as it has dif-
ferent members on each side of the equation, permit-
ting solutions via simultaneous equations. The first
four rules are concerned with interchange (commuta-
tivity), associativity and permutation.
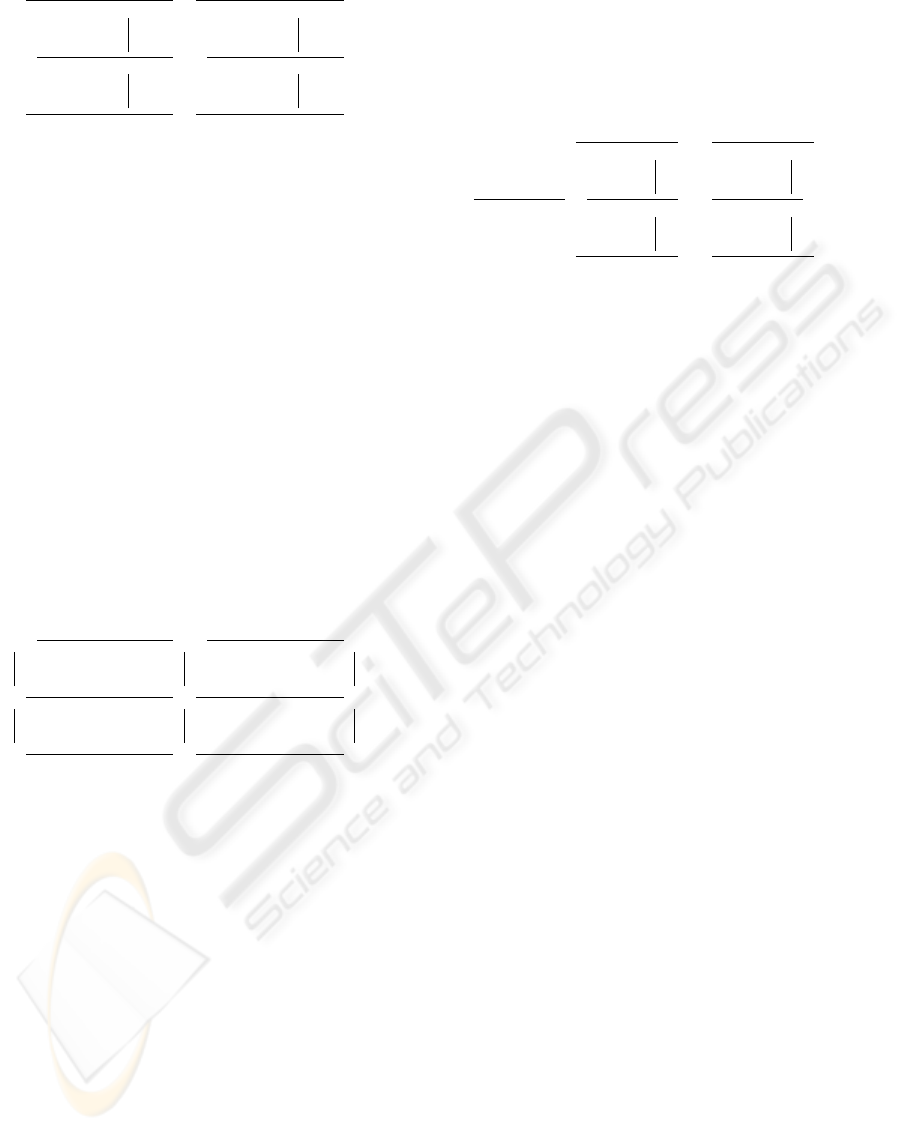
Simmons ((Simmons, 1989) section 3.8) also deals
with Godement’s rules. For a simplified version of
Figure 5, omitting categories A, E and functors E, H,
as shown in Figure 6, he derives the commuting dia-
gram of Figure 7 to represent the composition of func-
tors and natural transformations.
ICEIS 2005 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
94
B C D
F
2
G
2
α γ
F
3
β
G
3
δ
F
1
G
1
- -
- -
- -
? ?
? ?
Figure 6: Godement in (Simmons, 1989) section 3.8
The commuting properties are shown in the dia-
gram in Figure 7. A small change in Simmons’ no-
tation has been made so that pairs beginning with a
natural transformation have the subsequent functor in
subscript form to indicate that the object of the natural
transformation is the functor ((Barr and Wells, 1999),
1st ed., p.94-95). Where the pairs begin with a functor
the notation is unchanged as it appropriately indicates
the application of a functor to the output from a nat-
ural transformation.
The composition, say λ, of (δ ∗ γ) ◦ (β ∗ α) fol-
lows the path from G
1
F
1
−→ G
1
F
2
−→ G
1
F
3
−→
G
2
F
3
−→ G
3
F
3
; that, say ρ, of (δ ◦ β) ∗ (γ ◦ α) fol-
lows the path from G
1
F
1
−→ G
1
F
2
−→ G
2
F
2
−→
G
2
F
3
−→ G
3
F
3
. Both routes start and end with the
same objects G
1
F
1
and G
3
F
3
respectively. Hence
they are equivalent and the interchange law is demon-
strated with λ = ρ.
G
1
F
1
G
1
F
2
G
1
F
3
G
2
F
1
G
2
F
2
G
2
F
3
G
3
F
1
G
3
F
2
G
3
F
3
G
1
α G
1
β
G
2
α G
2
β
G
3
α G
3
β
γ
F
1
γ
F
2
γ
F
3
δ
F
1
δ
F
2
δ
F
3
- -
- -
- -
? ? ?
? ? ?
Figure 7: Commuting Diagram in (Simmons, 1989) section
3.8
3 APPLICATION
The consequence of natural closure is that a categori-
cal approach ensures that the various arrows of differ-
ent types can be composed with each other, irrespec-
tive of their level in the system. Equations represent-
ing an equality of paths, can be solved for unknown
components that can be determined from an evalua-
tion of the known properties. For instance in com-
paring methods with the path IOP from CPT −→
CST −→ SCH −→ DAT defining one approach,
then the path I
′
O
′
α from CPT −→ CST
′
−→
SCH
′
−→ DAT
′
might define an alternative ap-
proach if P
′
maps onto constructs in the category
CST
′
.
The diagram in Figure 8 shows the application of
the Godement calculus to handle semantic interop-
erability, defined as the interoperation of one system
with another at the level of meaning of the data, that
is at the metadata level.
CPT CST SCH DAT
P O
or
I
or
α
′′
α
′
O
oo
β
′
I
oo
β
′′
O
r
I
r
- - -
- -
- -
? ?
? ?
Figure 8: Semantic Interoperability in terms of Godement
The composition of the top line of functors I
r
◦O
r
◦
P gives the mapping from concepts to data for say
a relational system r. The composition of the mid-
dle line of functors I
or
◦ O
or
◦ P gives the mapping
from concepts to data for say an object-relational sys-
tem or. The composition of the bottom line of func-
tors I
oo
◦ O
oo
◦ P gives the mapping from concepts
to data for say an object-oriented system oo. Com-
paring these compositions gives a framework for in-
teroperability. For instance the natural transforma-
tion α
′
compares how the mapping is performed from
constructions to types in a relational system r with
that from constructions to types in an object-relational
system or. The natural transformation β
′′
compares
how the mapping is performed from types to data in
an object-relational system or with that from types to
data in an object-oriented system oo. The advantage
of the Godement approach is that arrows of any type
can be composed with each other so that any route can
be taken through the various mappings. The diagram
in Figure 7 shows that a number of commuting equa-
tions can be derived, enabling solution of equations
for unknown values. For instance β
′′
◦ β
′
compares
the mapping from constructions to data in an object-
relational system or with that in an object-oriented
system oo.
To extend the categorical framework to handle or-
ganisational interoperability, defined as the interoper-
ation of systems at the business process level, we need
to vary the functor P for each environment so that the
metameta level is variable. The required diagram is
shown in Figure 9.
The following canonical rules hold according to the
Godement calculus:
(β
′
◦ α
′
)(β ◦ α) = (β
′
β) ◦ (α
′
α) (6)
(I
or
◦ O
r
)α = I
or
(O
r
α) (7)
CONDITIONS FOR INTEROPERABILITY
95

CPT CST SCH DAT
P
or
P
oo
P
r
O
or
I
or
α
′
α
′′
O
oo
β
′
I
oo
β
′′
O
r
I
r
α
β
-
-
-
- -
- -
- -
? ?
? ?
?
?
Figure 9: Organisational Interoperability in terms of Gode-
ment
α
′
(O
r
◦ P
or
) = (α
′
O
r
)P
or
(8)
I
r
(β
′
◦ α
′
)P
or
= (I
r
β
′
P
or
) ◦ (I
r
α
′
P
or
) (9)
α
′′
α
′
= (α
′′
O
or
) ◦ (I
r
α
′
) = (I
or
α
′
) ◦ (α
′′
O
r
) (10)
A number of general principles in composition are
shown by the equations. Equation 6 indicates that of
commutativity (the interchange law); equations 7. . .8
indicate that of associativity; equation 9 indicates that
of permutation of paths. The last equation, 10, shows
the production of simultaneous equations represent-
ing different paths through the diagram. This is an im-
portant feature as it facilitates the solution for an un-
known mapping. For example, in equation 10 above,
if the values α
′
, α
′′
and I
or
are known, then O
r
is the
only unknown and a solution can be found for it. That
is if it is known how the mapping from constructions
to types and from types to data varies between a rela-
tional system r and an object-relational system or and
what the mapping is between types and data in an ob-
ject relational system or, then the mapping between
constructions and types in the relational system r can
be derived.
4 SEMANTIC
INTEROPERABILITY
The foregoing indicates that semantic interoperability
can be guaranteed therefore for a system that imple-
ments in full formal form the four-level categorical
diagram and approach as just described. In particular
all compositions of arrows (identity, function, func-
tor, natural transformation) must be natural, that is all
diagrams must commute. Semantic interoperability
depends on the horizontal and vertical composition
of both syntactical and semantic diagrams as well as
the interaction (contravariant) between the syntacti-
cal and the semantic. The semantics involve instan-
tiation everywhere, that is local extensionalities in-
terconnected one with another through global inten-
sionality. We have not explicitly mentioned the usual
point (because reality is equivalent to naturality in cat-
egory theory) that all the categories already referred to
in this paper are cartesian closed. In formal terms of
category theory, this further condition for global con-
nectivity in interoperability means that the categories
need to also be locally cartesian closed. This prop-
erty connects and integrates in a coherent way slice
categories
1
.
The method of semantic annotation as advanced at
present appears to be a local method carried out either
manually or by some automated agents. This will be
very reductionist but may be quite sufficient if carried
out at run time.
Linked with the typing problems exhibited in punc-
tured diagrams, there is the whole question of the cap-
ture of type information. Semantic interoperability
depends on as complete a picture as possible being
obtained of types in the different systems. Semantic
annotation is employed in the semantic web (Hendler
et al., 2002) and in other techniques such as metadata
creation (Soo et al., 2003) where agents are used to
explore the data structures for type information.
For semantic annotation we are investigating the
use of natural database techniques (Rossiter and
Heather, 2004) to see how much of such informa-
tion can be collected automatically through analysis
of the data in a categorical framework. Collection
of metameta data is essentially an open architecture
task and we intend to employ the categorial topos and
its internal intuitionistic logic i.e. Heyting (Lane and
Moerdijk, 1991; Johnstone, 2002) for this purpose.
5 COMPOSITION FAILURE
Composition is only certain for categories with ar-
rows as properly defined (Simmons, 1989). Figure
1 is not a formal diagram and the arrows in that fig-
ure for the classical ANSI/SPARC architecture often
do not satisfy such requirements. Implementations of
database schemas typically make use of partial func-
tions in a reductionist view of real-world naturality.
For instance the relational data model of Codd has
had to be compromised for the various SQL standards
(Date and Darwen, 2000). Partial functions are in
such common use in mathematical modelling that var-
ious attempts have been made to carry them over into
the use of category theory. Peter Freyd, an early cate-
gorist pioneer, has proposed that composition failure
be acknowledged in formal diagrams by a puncture
mark.
1
Barr & Wells provide a comprehensive definition of lo-
cally cartesian closed categories ((Barr and Wells, 1999),
3rd ed.) and the significance of slice categories in computer
science is extensively dealt with by (Goguen and Burstall,
1984).
ICEIS 2005 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
96
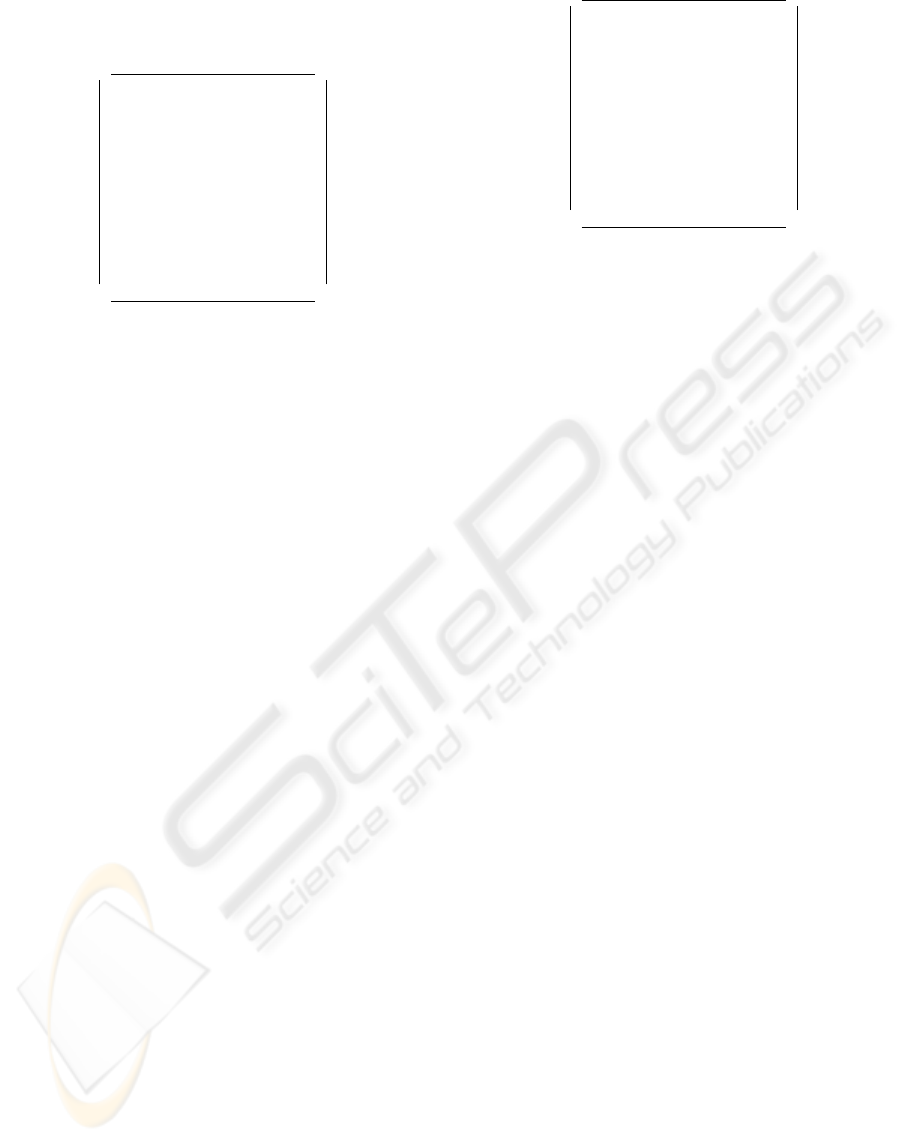
5.1 Punctured Diagrams
A B
DC
xu
y
t
z
L
-
-
? ?
@
@
@
@
@
@
@
@
@
@
@R
Figure 10: Punctured Commuting Diagram
A commuting diagram is itself a proof of some nat-
urality. A weaker version of the commuting diagram
may be represented by the punctured diagram pro-
moted by ((Freyd and Scedrov, 1990) section 1.251)
as in Figure 10 where the puncture mark
L
removes
the commutation of the right-hand triangle although it
retains the commutation of the left-hand triangle and
the commutation of the rectangle as a whole. That is
the puncture sign
L
removes the equivalent of one
equation. A weakness of punctured diagrams is that
which diagram is punctured is not always explicitly
shown. What about the outer square in Figure 10?
Does it need a separate puncture mark? In databases
there are examples where the puncture might be used,
for instance, with the problem of representing partial
functions. If in Figure 11, ST K is a library stock,
ISS is the category of books issued on loan at the
current time, CAT is the catalogue, ACC is the ac-
cession numbers, then t is a total function from CAT
to ACC, u is a total function from ST K to CAT , x
is a total function from ISS to ACC and z is a total
function from ST K to ACC. y is, however, a partial
function from ST K to ISS as not all books will be
out on loan at any one time. If all the functions were
total, then z = tu = xy so we have three commut-
ing equations: z = tu, z = xy and tu = xy. With
the partial function y, then we lose the commuting
equation z = xy but retain z = tu. The outer dia-
gram will still commute if ACC is derived indepen-
dently of ISS so we have lost one commuting equa-
tion, hence the one puncture mark.
Punctured diagrams represent a type failure in a
category: the type of an input is unexpected and
an appropriate output cannot be generated. One of
the causes shown here of partial functions could be
avoided by making all functions total as is usual in
category theory. Source objects that are unassigned
ST K ISS
ACCCAT
xu
y
t
z
L
-
-
? ?
@
@
@
@
@
@
@
@
@
@
@R
Figure 11: Punctured Commuting Diagram for Library Ex-
ample
ACC = accessions, ST K = stock, ISS = issues, CAT =
catalogue
by the function in its normal operation may then be
assigned to the initial object (⊥) so that a complete
assignment is made of objects in the source category.
In categorical terms, type forcing is necessary to avoid
punctured diagrams and maintain interoperability.
5.2 Lifted Categories and Sketches
There are alternative approaches to composition fail-
ure in category theory. Two of these have been the
focus of database workers.
(Lellahi and Spyratos, 1990), in the FIDE project,
attempted to adapt category theory to partial functions
by creating a new categorical type of lifted (or partial)
functions. This technique has not been further devel-
oped, perhaps because of its inherent complexity and
its conflict with much of the established theory of cat-
egories.
Sketches have had more advocates. The reduction-
ism of set theoretic methods to represent real-world
activities means that corresponding categories may
not commute because of the departure from natural-
ity. The purpose of sketches was to identify, as in
punctured diagrams, the departures from naturality in
the internal components of a diagram like the cones
and cocones. For instance (Johnson et al., 2002)
applied sketches to entity-relationship and relational
modelling and (Diskin and Cadish, 1995) to object
databases.
Sketches are strictly outside category theory as they
permit diagrams that do not commute but they may
be mapped onto categories by a model functor. Many
types of sketches have been developed in the theory
itself. For instance (Johnstone, 2002) defines eight at
D2.1.3 2 p.863-864. They separate out four compo-
nents of a diagram in order to flag the parts for which
composition fails. These four components may be de-
fined as a 4-tuple < E, L, R, S > where E is a finite
graph for the data structure, L is a set of diagrams in
E giving the constraints as commuting diagrams, R
CONDITIONS FOR INTEROPERABILITY
97
is a finite set of discrete cones in E giving the rela-
tionships and S a finite set of discrete cocones in E
specifying the attributes. For example the omission
of a diagram from L means that it is not required to
commute, so this diagram is effectively punctured.
Sketches lack flexibility as all structures and con-
straints have to be pre-specified. In difficult ar-
eas such as interoperability, sketches are inadequate
as they do not offer natural closure. (Johnson and
Rosebrugh, 2000) attempt to adapt their sketches to
achieve interoperability but the aim is to achieve only
logical independence, as in the three-level architec-
ture of Figure 1, not semantic interoperability, as in
the four-level architecture of Figure 2. The difference
between a natural structure and a sketch is like that be-
tween typing and labelling. A graph is richer than an
entity-relationship model as its arrows are typed with
identity functors. Labelling in the entity-relationship
model is an informal typing whereas the identity ar-
row is a formal typing.
6 NATURAL COMPOSITION
Some problems with partial functions can be avoided
by altering the data design so that the partial functions
only operate in the assignment to the end of the chain
(the terminal object). For instance an alternative de-
sign can be considered for Figure 11. Here the natural
order would be to consider first accessions, which are
then put into the stack and can be issued later. For this
schema the composition diagram would be as in Fig-
ure 12. These are full categories without composition
failure and the puncture sign can be removed. There
are no punctured diagrams if ISS is the codomain of
each of x
′
, t
′
and z
′
. This is because these are all par-
tial functions, mapping onto a category which is last
in the sequence, the terminal object. There is a type
change but it occurs just once, in the final step. It
is when partial functions map onto intermediate cat-
egories in a chain that typing problems are likely to
occur, because of the fluctuations of the types.
7 CONCLUSIONS
The use of a formal four-level architecture, based on
category theory, provides an encouraging framework
for tackling both semantic and organisational inter-
operability. The use of the Godement calculus, in
particular, enables many different paths at a number
of level to be compared and analysed. A number of
problems remain. Failure of composition, particularly
due to the existence of partial functions, needs to be
ACC ST K
ISSCAT
x
′
u
′
y
′
t
′
z
′
-
-
? ?
@
@
@
@
@
@
@
@
@
@
@R
Figure 12: Non-punctured Commuting Diagram for Library
Example
ACC = accessions, ST K = stock, ISS = issues, CAT =
catalogue
identified. Punctured categorical diagrams are used
for this purpose in preference to lifted categories or
sketches. Semantic annotation remains a challenging
area where the open Heyting logic may be of assis-
tance.
REFERENCES
Barr, M. and Wells, C. (1999). Category Theory for
Computing Science. Les Publications Centre de
Recherches Math
´
ematiques, Montr
´
eal, 3rd (earlier
editions prentice-hall, 1990, 1995), edition.
Date, C. and Darwen, H. (2000). Foundation for Future
Database Systems: The Third Manifesto. Addison
Wesley, 2nd edition.
Diskin, Z. and Cadish, B. (1995). Algebraic graph-based
approach to management of multidatabase systems.
NGITS’95, pages 69–79.
Freyd, P. and Scedrov, A. (1990). Categories, Allegories.
North-Holland.
Godement, R. (1958). Th
´
eorie des faisceaux. Hermann.
Goguen, J. and Burstall, R. (1984). Some fundamental al-
gebraic tools for the semantics of computation. part 1:
Comma categories, colimits, signatures and theories.
Theor Comp Sci, 31:175–209.
Heather, M. and Rossiter, B. (2002). The anticipatory and
systemic adjointness of e-science computation on the
grid. Computing Anticipatory Systems, Proceedings
CASYS‘01, AIP Conference Proceedings, 627:565–
574.
Hendler, J., Berners-Lee, T., and Miller, E. (2002). Inte-
grating applications on the semantic web. J Institute
Electrical Engineers, 122(10):676–680.
Johnson, M. and Rosebrugh, R. (2000). Database interoper-
ability through state based logical data independence.
Proc 4th CSCW2000, pages 161–166.
Johnson, M., Rosebrugh, R., and Wood, R. (2002). Entity-
relationship-attribute designs and sketches. TAC,
10:94–111.
ICEIS 2005 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
98

Johnstone, P. (2002). Sketches of an Elephant, A Topos The-
ory Compendium, Oxford Logic Guides 43. Claren-
don, Oxford.
Kelly, G. and Street, R. (1974). Review on the elements
of 2-categories,. Proceedings Sydney Category The-
ory Seminar 1972-73, Lecture Notes in Mathematics,
Springer-Verlag, 420:75–103.
Lane, S. M. and Moerdijk, I. (1991). Sheaves in Geometry
and Logic. Springer-Verlag.
Lellahi, S. and Spyratos, N. (1990). Towards a categorial
data model supporting structured objects and inheri-
tance. East/West Database Workshop, pages 86–105.
Rossiter, B. and Heather, M. (2004). Data structures in nat-
ural computing: Databases as weak or strong anticipa-
tory systems. CASYS’03, Sixth International Confer-
ence on Computing Anticipatory Systems, Li
`
ege, Bel-
gium, AIP Conference Proceedings, 718:392–405.
Rossiter, N. (2003). From classical to quantum databases
with applied pullbacks. 78th Meeting Peripatetic Sem-
inar on Sheaves and Logic, Institut de Recherche
Math
´
ematique Avanc
´
ee,Strasbourg University 15-16
February.
Rossiter, N. and Heather, M. (2003). Four-level architec-
ture for closure in interoperability. EFIS2003, Fifth
International Workshop on Engineering Federated In-
formation Systems, Coventry, UK, 17-18 July, pages
83–88.
Simmons, H. (1989). Lecture notes on category theory.
Logic in IT Initiative, SERC.
Soo, V., Lee, C., Li, C., Chen, S., and Chen, C. (2003).
Automated semantic annotation and retrieval based on
sharable ontology and case-based learning techniques.
Int Conf Digital Libraries Archive, pages 61–72.
Tsichritzis, D. (1978). Ansi/x3/sparc dbms framework
1978, report of the study group on database manage-
ment systems. Information Systems, 3.
CONDITIONS FOR INTEROPERABILITY
99
