
USING dmFSQL FOR FINANCIAL CLUSTERING
Ramón Alberto Carrasco
Dpto. de Lenguajes y Sistemas Informáticos, Universidad de Granada, Granada, Spain
María Amparo Vila
Dpto. de Ciencias de la Computación e I.A., Universidad de Granada, Granada, Spain
José Galindo
Dpto. de Lenguajes y Ciencias de la Computación, Universidad de Málaga, Spain
Keywords: Clustering, Flexible Queries, Data Mining, Fuzzy SQL, Fuzzy Databases.
Abstract: At present, we have a dmFSQL server available for Oracle© Databases, programmed in PL/SQL. This
s
erver allows us to query a Fuzzy or Classical Database with the dmFSQL (data mining Fuzzy SQL)
language for any data type. The dmFSQL language is an extension of the SQL language, which permits us
to write flexible (or fuzzy) conditions in our queries to a fuzzy or traditional database. In this paper, we
propose the use of the dmFSQL language for fuzzy queries as one of the techniques of Data Mining, which
can be used to obtain the clustering results in real time. This enables us to evaluate the process of extraction
of information (Data Mining) at both a practical and a theoretical level. We present a new version of the
prototype, called DAPHNE, for clustering witch use dmFSQL. We consider that this model satisfies the
requirements of Data Mining systems (handling of different types of data, high-level language, efficiency,
certainty, interactivity, etc) and this new level of personal configuration makes the system very useful and
flexible.
1 INTRODUCTION
We can define Data Mining as the process of
extraction of interesting information from the data in
databases. According to (Frawley 1991) a
discovered knowledge (pattern) is interesting when
it is novel, potentially useful and non-trivial to
compute. A serie of new functionalities exist in Data
Mining, which reaffirms that it is an independent
area (Frawley 1991):
- High-Level Language. This representation is
d
esirable for discovered knowledge and for showing
the results of the user's requests for information (e.g.
queries).
- Certainty. The discovered knowledge should
accurately re
flect the content of the database. The
imperfectness (noise and exceptional data) should be
expressed with measures of certainty.
- Efficiency. The process of extraction of
k
nowledge should be efficient, i.e. the running time
should be predictable and acceptable when dealing
with very large amounts of data.
- Handling of Different Types of Data. There are
di
fferent kinds of data and databases used in diverse
applications (relational data, objects, hypertext, etc.)
so it would be desirable that a Data Mining system
would carry out its work in an effective way.
- Interactive Mining Knowledge at Multiple
Ab
straction Levels. The interactive discovery of
knowledge allows the user to refine a Data Mining
request on line, dynamically change data focusing,
progressively deepen a Data Mining process, and
flexibly view the data and Data Mining results at
multiple abstraction levels and from different angles.
- Mining Information from Different Sources of
Data. Cu
rrently the knowledge mining from
different sources of formatted or unformatted data
135
Alberto Carrasco R., Amparo Vila M. and Galindo J. (2005).
USING dmFSQL FOR FINANCIAL CLUSTERING.
In Proceedings of the Seventh International Conference on Enter prise Information Systems, pages 135-141
DOI: 10.5220/0002526801350141
Copyright
c
SciTePress
with diverse data semantic is perceived to be a
difficult challenge.
In this paper we discuss the implementation of
two prototypes for Data Mining purposes: we have
used a combination of DAPHNE which was initially
designed for clustering on numeric data types
(Carrasco, 1999) and dmFSQL which was designed
for fuzzy (or flexible) queries (Galindo 1998,
Galindo 1998b, Galindo 1999). At this point, we
would like to point out that Data Mining is an
autonomous and self-interesting field of research, in
which techniques from other fields could be applied.
Among these techniques are the use of dmFSQL
(data mining Fuzzy SQL), which is a database query
language which incorporates fuzzy logic. In
particular, we use dmFSQL to solve, in real time,
queries, which obtain objects (tuples) with similar
characteristics, i.e. objects of a specific group
through a process of clustering. Often, the clustering
is carried out on a set of examples from the database
and not on the entire database. We present some
experimental results with this alternative solution in
the context of a bank. This area needs a Data Mining
system tailored to its needs, because this area
manages very large databases and these data has a
very concrete meaning. Thus, data must be treated
according to this meaning. Finally, as conclusions
we consider that this model satisfies the
requirements of Data Mining systems [Chen 1996,
Frawley 2001) (handling of different types of data,
high-level language, efficiency, certainty,
interactivity, etc.) and this new level of personal
configuration makes the system very useful and
flexible.
2 dmFSQL A LANGUAGE FOR
FLEXIBLE QUERIES
The dmFSQL language (Galindo 1998, Galindo
1998b, Galindo 1999) extends the SQL language to
allow flexible queries. We have extended the
SELECT command to express flexible queries and,
due to its complex format, we only show an abstract
with the main extensions added to this command:
- Linguistic Labels: If an attribute is capable of
undergoing fuzzy treatment then linguistic
labels can be defined on it. These labels will be
preceded with the symbol $ to distinguish them
easily. They represent a concrete value of the
attribute. dmFSQL works with any kind of
attributes (see 2.1.1 section) therefore, by
example, a label can have associated: a
trapezoidal possibility (Figure 1), a scalar (if
there is a similarity relationship defined
between each two labels in the same domain), a
text, a XML document, etc.
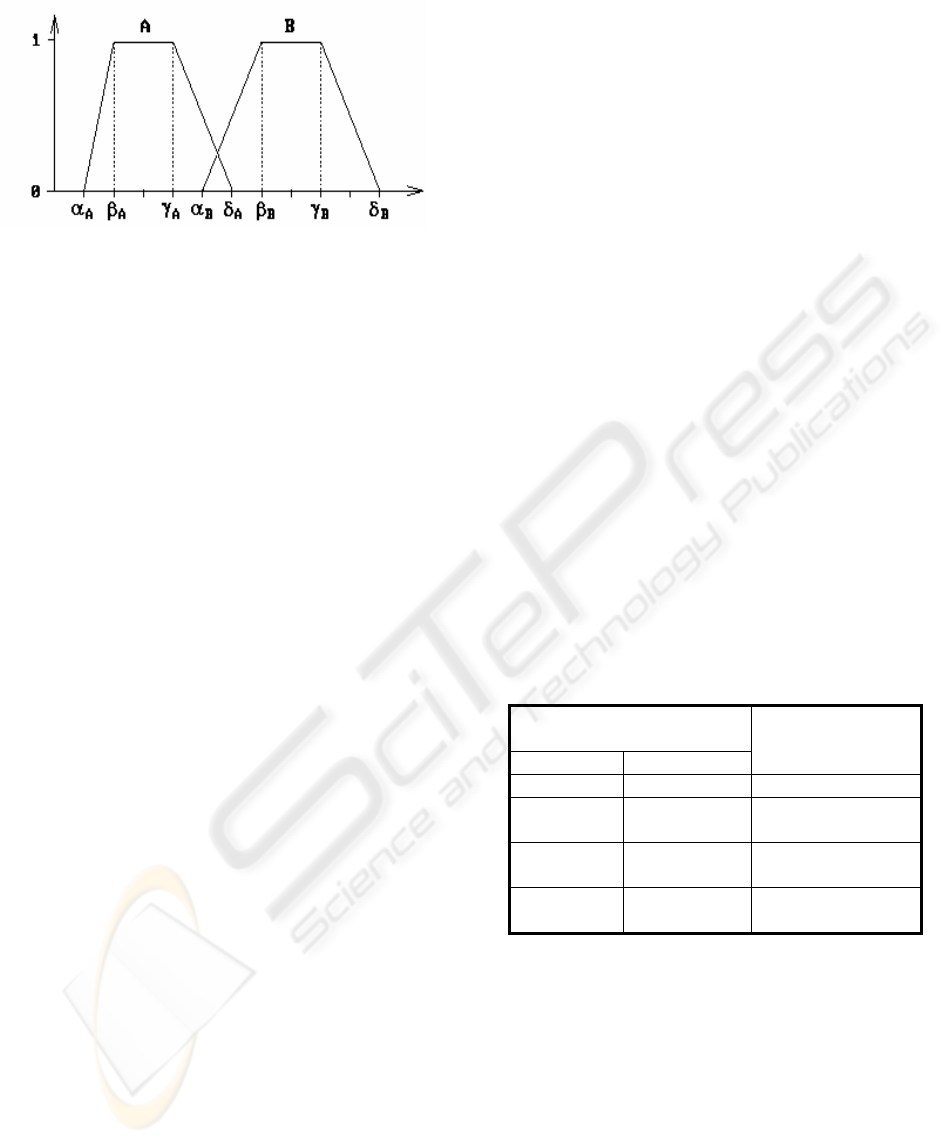
Figure 1: Trapezoidal possibility distributions: A, B
- Fuzzy Comparators: In addition to common
comparators (=, >, etc.), dmFSQL includes
fuzzy comparators in Table 1. There are some
different kinds of fuzzy comparators. By
example a fuzzy comparator is used to compare
two trapezoidal possibility distributions A, B
with A=$[α
A
,β
A
,γ
A
,δ
A
] B=$[α
B
,β
B
,γ
B
,δ
B
] (see
Figure 1). In the same way as in SQL, fuzzy
comparators can compare one column with one
constant or two columns of the same type. More
information can be found in (Galindo 1998b,
Galindo 1999). These definitions can are based
in fuzzy set theory, classical distance functions
and other type of similarity functions.
Table 1: Fuzzy Comparators for dmFSQL
Fuzzy Comparator (fcomp)
for:
Possibility Necessity
Significance
FEQ NFEQ Fuzzy EQual
FGT
FGEQ
NFGT
NFGEQ
Fuzzy Greater Than
Fuzzy Greater or Equal
FLT
FLEQ
NFLT
NFLEQ
Fuzzy Less Than
Fuzzy Less or Equal
MGT
MLT
NMGT
NMLT
Much Greater Than
Much Less Than
- Fulfilment Thresholds γ: For each simple
condition a Fulfilment threshold may be
established with the format <condition>
THOLD
γ
, indicating that the condition must be
satisfied with a minimum degree γ in [0,1]
fulfilled.
- CDEG(<attribute>) function: This function
shows a column with the Fulfilment degree of
the condition of the query for a specific
attribute, which is expressed in brackets as the
argument.
- Fuzzy Constants: We can use and store all of
the fuzzy constants (which appear in Table 2) in
ICEIS 2005 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
136
dmFSQL.
Table 2: Fuzzy Constants of dmFSQL
F. Constant Significance
UNKOWN
UNDEFINED
NULL
Unknown value but the attribute is applicable
The attribute is not applicable or it is meaningless
Total ignorance: We know nothing about it
A=$[α
A
,β
A
, γ
A
,δ
A
]
$label
[n, m]
#n
Fuzzy trapezoid (α
A
≤β
A
≤ γ
A
≤δ
A
): See Figure 1
Linguistic Label: It may be a trapezoid or a scalar
(defined in dmFMB)
Interval “Between n and m” (α
A
=β
A
=n and
γ
A
=δ
A
=m)
Fuzzy value “Approximately n” (β
A
=γ
A
=n and n-
α
A
=δ
A
=margin)
2.1 Architecture of dmFSQL
In this section, we shall describe the first prototype
to be integrated in our approach. At present, we have
a dmFSQL Server available for Oracle© Databases,
mainly programmed in PL/SQL. The architecture of
the Fuzzy Relational Database with the dmFSQL
Server is made up by:
1. Data: Traditional Database and data mining
Fuzzy Meta-knowledge Base (dmFMB).
2. dmFSQL Server.
2.1.1 Data: Traditional Database and dmFMB
The data can be classified in two categories:
- Traditional Database: They are data from our
relations with a special format to store the fuzzy
attribute values. The fuzzy attributes are
classified by the system in 4 types:
- Fuzzy Attributes Type 1: These attributes
are totally crisp (traditional), but they have
some linguistic trapezoidal labels defined on
them, which allow us to make the query
conditions for these attributes more flexible.
Besides, we can use all constants in Table 2 in
the query conditions with these fuzzy
attributes.
- Fuzzy Attributes Type 2: These attributes
admit crisp data as well as possibility
distributions over an ordered underlying
domain. With these attributes, we can store and
use all the constants we see in Table 2.
- Fuzzy Attributes Type 3: These attributes
have not an ordered underlying domain. On
these attributes, some labels are defined and on
these labels, a similarity relation has yet to be
defined. With these attributes, we can only use
the fuzzy comparator FEQ, as they have no
relation of order. Obviously, we cannot store or
use the constants fuzzy trapezoid, interval and
approximate value of Table 2.
- Attributes Type 4: There are different kinds
of data in a database used in diverse
applications (relational data, objects, hypertext,
XML, etc.) therefore, it would be desirable that
a Data Mining system would carry out its work
in an effective way. In order to manage these
data we have defined these attributes. It is a
generic type (fuzzy or crisp), which admits
some fuzzy treatment. We permitted this
attribute is formed by more than a column of
the table (complex attributes). Therefore, with
attributes Type 4 is possible to redefine the
attributes Type 1, 2 and 3 using other
representations (by example, alternative
representation to the fuzzy trapezoid) or fuzzy
comparators. With these attributes, we can
store and use the constants linguistic label in
Table 2.
- data mining Fuzzy Meta-knowledge Base
(dmFMB): It stores information about the Fuzzy
Relational Database in a relational format. It
stores attributes which admit fuzzy treatment
and it will store different information for each
one of them, depending on their type:
- Fuzzy Attributes Type 1: In order to use
crisp attributes in flexible queries we will only
have to declare them as being a fuzzy attribute
Type
1 and store the following data in the dmFMB:
Trapezoidal linguistic labels: Name of the label
and α
A
, β
A
, γ
A
and δ
A
values (as in Figure 1).
Value for the margin of the approximate values
(see Table 1). Minimum distance in order to
consider two values very separated (used in
comparators MGT/NMGT and MLT/NMLT).
- Fuzzy Attributes Type 2: As well, as
declare them as being a fuzzy attribute Type 2,
these attributes have to store the same data in
the
dmFMB as the fuzzy attributes Type 1.
- Fuzzy Attributes Type 3: They store in the
dmFMB their linguistic labels, the similarity
degree amongst themselves and the
compatibility between attributes of this type,
i.e., the attributes that use the same labels and
that can be compared amongst them.
- Attributes Type 4: The dmFMB stores
information for the fuzzy treatment of the
attributes Type 4:
- Fuzzy Comparison Functions: The
user can define the functions of comparison
(Table 1) for the treatment of each attribute
of Type 4. The format is: CDEG (A fcomp
B) -> [0,1] with CDEG the compatibility
degrees, A, B two attributes or linguistic
USING dmFSQL FOR FINANCIAL CLUSTERING
137

labels Type 4 and fcomp any fuzzy
comparator in Table 1. The user can
associate each attribute functions already
defined in the dmFMB.
- Representation Functions: The user
can optionally define it to show the
attributes in a more comprehensible way.
Of course, the user can associate each
attribute functions already defined in the
dmFMB
- Linguistic labels: They represent a
concrete value of the attribute.
- Complex attributes: We permitted this
attribute is formed by more than a column
of the table. Therefore, the dmFMB stores
information on structure of the attributes
Type 4.
2.1.2 dmFSQL Server
It has been programmed mainly in PL/SQL and it
includes three kinds of functions for attributes Type
1, Type 2 and Type 3:
- Translation Function: It carries out a lexical,
syntactic and semantic analysis of the dmFSQL
query. If errors, of any kind whatsoever, are found, it
will generate a table with all the found errors. If
there are no errors, the dmFSQL query is translated
into a standard SQL sentence. The resulting SQL
sentence includes reference to the following kinds of
functions.
- Representation Functions: These functions are
used to show the fuzzy attributes in a
comprehensible way for the user and not in the
internally used format.
- Fuzzy Comparison Functions: They are utilized
to compare the fuzzy values and to calculate the
compatibility degrees (CDEG function).
As we have seen, Translation and Representation
Functions are included in the dmFMB for the
attributes Type 4.
3 USING dmFSQL TO
CLUSTERING PROCESS
In this section, we shall describe the integration of
dmFSQL Server to the clustering process. This is a
part of a project, which is currently under
investigation with some Spanish banks. It deals with
customer database segmentation, which allows
differentiated treatment of customers (Direct
Marketing).
Included in this project we have a prototype
called DAPHNE (Carrasco, 1999). It is a generic
tool for clustering focused on the financial
environment. The prototype uses techniques, which
come from diverse fields: hierarchical clustering,
unsupervised learning based on fuzzy-set tools,
statistical techniques, etc. In this paper, we show a
new version of DAPHNE witch incorporate the
dmFSQL Server to do effective clustering.
Following we explain the full process.
Operation of DAPHNE: In the first step, the
relevant features of the customers for the clustering
are chosen using the user's knowledge. For this
selection, the user can use a method that we have
developed for automatic selection of relevant
characteristics based on genetic algorithms (Martín-
Bautista 1998). Therefore, the user inserts a new
project for clustering in the meta-database of the
prototype specifying the table or view with the
source data (id_table_clustering) and the attributes,
which DAPHNE will use for the clustering
(col_clu
1
, col_clu
2
,…, col_clu
m
). Theses attributes
have to define in the dmFMB as Type 1, 2, 3 or 4
specifying their characteristics. The user does not
need to specify anything on the domains of the
previously used attributes. It is important to note that
they are not restriction: on the type of attributes to
use for the clustering process (text, scalar, binary,
numerical, etc) and the on possible uncertainty of the
value of this attributes (unknown, undefined, null
and certain degree of belong). Besides the user
specify the weight of each attributes in the clustering
process (w_clu
1
, w_clu
2
,…, w_clu
m
such that w_clu
r
∈ [0,1] with r=1..m and verifying )
∑
=
=
m
r
r
cluw
1
1 _
Subsequently the main processes of DAPHNE are
explained, as well as its underlying theoretical base:
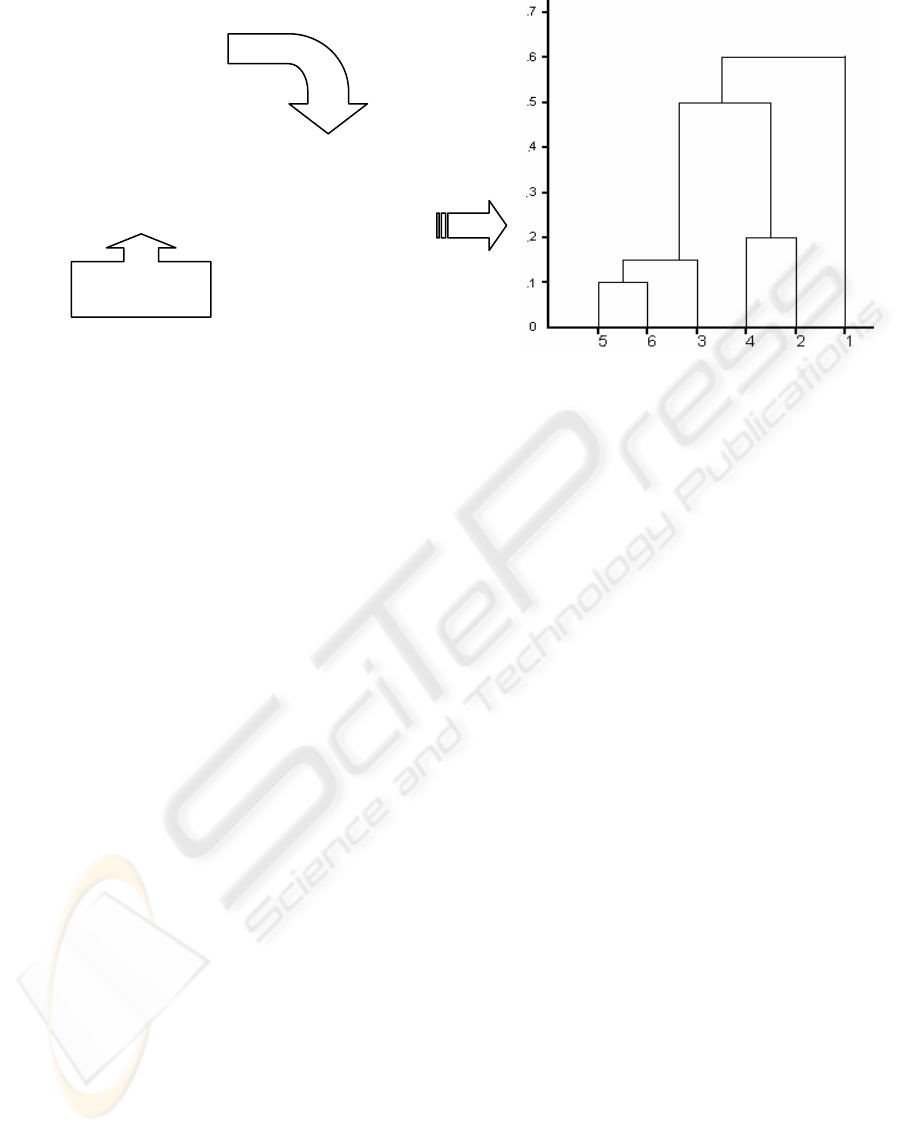
1. Computing Ultrametric Distance Matrix (see
Figure 2): This process attempts to obtain the
population's ultrametric distance matrix. Since the
results by Dunn, Zadeh y Bezdek (Delgado 1996)
it has been well known that there is equivalence
between hierarchical clustering, max-min
transitive fuzzy relation, and ultrametric
distances. Therefore, in the ultrametric matrix all
the possible clustering that can be carried out on
the population specified. The “dendogram" or
“tree diagram" may be viewed as a diagrammatic
representation of the results of a hierarchical
clustering process which is carried out in terms of
the distance matrix. This process contains the
following treatments:
ICEIS 2005 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
138
Benzécri
dmFS
Q
L
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
=
0
1.0
5.7.0
2.15.6.0
6.5.2.5.0
7.6.7.6.7.0
D
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
=
0
1.0
5.5.0
15.15.5.0
5.5.2.5.0
6
.6.6.6.6.0
'D
Figure 2: Computing a ultrametric distance
m
atrix (dendograme) for six elements
- Computing population's normalized (in [0,1])
distance matrix (by example, the matrix D in
Figure 2). For each pair of the population's
individuals (i, j) the distance that separates both
(d
ij
) is obtained using dmFSQL as following:
SELECT A1.ROW_ID AS i, A2.ROW_ID AS j,
1-(CDEG(A1.col_clu
1
)* wclu
1
+…+
CDEG(A1. col_clu
m
)* w_clu
m
) AS d
ij
,
FROM id_table_clustering A1,
id_table_clustering A2
WHERE A1.ROW_ID < A2.ROW_ID
AND (A1.col_clu
1
fuzzy_ecomp
1
A2.col_clu
1
THOLD 0
| A1.col_clu
1
fuzzy_ecomp
1
A2.col_clu
1
THOLD 0
AND
A2.col_clu
1
fuzzy_ecomp
1
A1.col_clu
1
THOLD 0
| A1.col_clu
1
fuzzy_ecomp
1
A2.col_clu
1
THOLD 0
OR
A2.col_clu
1
fuzzy_ecomp
1
A1.col_clu
1
THOLD 0)
AND … AND
(A1.col_clu
m
fuzzy_ecomp
m
A2.col_clu
m
THOLD 0
| A1.col_clu
m
fuzzy_ecomp
m
A2.col_clu
m
THOLD 0
AND
A2.col_clu
m
fuzzy_ecomp
m
A1.col_clu
m
THOLD 0
| A1.col_clu
m
fuzzy_ecomp
m
A2.col_clu
m
THOLD 0
OR
A2.col_clu
m
fuzzy_ecomp
m
A1.col_clu
m
THOLD 0);
where fuzzy_ecomp
r
is the fuzzy equal
comparator (FEQ or NFEQ) chosen for the user
for the fuzzy attribute col_clu
r
. For each attribute
col_clu
r
the WHERE clausule has three optional
forms (specified by | symbol):
a) If fuzzy_ecomp
r
is symmetric:
A1.col_clu
r
fuzzy_ecomp
r
A2.col_clu
r
THOLD 0
b) Using a T-norm if fuzzy_ecomp
r
is not
symmetric:
A1.col_clum fuzzy_ecomp
r
A2.col_clu
r
THOLD 0
AND
A2.col_clum fuzzy_ecomp
r
A1.col_clu
r
THOLD 0
c) Using a T-conorm if fuzzy_ecomp
r
is not
symmetric:
A1.col_clum fuzzy_ecomp
r
A2.col_clu
r
THOLD 0
OR
A2.col_clum fuzzy_ecomp
r
A1.col_clu
r
THOLD 0
- Computing population's ultrametric distance
matrix (by example, the matrix D’ in Figure 2). In
the distance matrix, each of the three elements
verifies the triangle inequality. The matrix is
transformed so that each of the three elements of
the ultrametric inequality is also verified. An
algorithm based on the method of Benzécri
(
Benzécri, 1976) is used. For this purpose, we use a
parallel algorithm using MPI (Quinn 2003).
2. Computing possible α -cuts: Since the ultrametric
matrix is finite, it contains only a finite set of
different values. Thus, for the hierarchical clustering
or ultrametric matrix we can always determine
unequivocally the set of all possible different α -
cuts, that is, the set of all different equivalence
relations associated with the matrix. In other words,
every α -cut implies a different partition or the
population's clustering. By example, in the Figure 2
the possible α -cuts are 0.1, 0.15, 0.2, 0.5 and 0.6.
3. Clustering: This process assigns each individual
in the population to a certain cluster. In order to do
so it is necessary to obtain a certain partition from
the ultrametric matrix. Therefore, the problem
consists of choosing an α -cut among the possible
α -cuts already obtained, according to the
hypothesis that no previous information about the
USING dmFSQL FOR FINANCIAL CLUSTERING
139
structure of the data is available. The partition can
be obtained in different ways according to the user's
choice:
- Absolute good partition. We obtain the partition
determined by the α -cut 0.5 (Vila 1979). By
example, in the Figure 2 the α -cut 0.5 determines
the classes {5, 6, 3} and {4, 2, 1}.
- A good partition. We use an unsupervised
learning procedure based on fuzzy-set tools. This
procedure determines a good partition as the
minimum value of a measure denned on the set of all
possible α -cuts (Delgado 1996).
- Partition that determines a certain number of
groups. By means of a binary search algorithm on all
possible α -cuts, we obtain the α -cut which
implies a number of groups which are closest to the
user's request.
4 EXPERIMENTAL RESULTS
This system has been applied to some problems of
the segmentation of bank customers in real life
situations. Here we show a particular case of
segmentation. The relevant attributes identified by
the banking expert have been:
- Payroll (payroll): is a binary attribute that
indicates if the client receives payroll through
the financial company (value 1) or not (value 0).
We decide define this attribute as Type 4
specifying a FEQ comparator in the dmFMB
based in the Sokal and Michener distance.
- Average account balance of the client in last 12
moths (balance): it is obtained through an
analytic study in the company data warehouse
system. This is a crisp attribute but we decide
define this as Type 1 in the dmFMB using the
f
uzzy constants value #n = 500 (approximately n,
see Table 2).
- Geographic area of clients (area): there are
three areas in the study: Madrid, Barcelona
(Spanish cities) and rest of World. Obviously,
this is a scalar attribute (Type 3), therefore we
define a similarity relationship for the FEQ
comparator in the dmFMB (see Table 3).
Table 3: Similarity relationship defined for area
area
Madrid Barcelona Rest of World
Madrid 1 0.6 0
Barcelona 1 0
Rest of World 1
Now we must specify the weight of each
attributes in the clustering process in order to better
focus the customers clustering according to the user
criteria. The weights chosen are 0.4 for area and
payroll and 0.2 for balance.
Finally, by means of a sample of a few tuples the
system here proposed has obtained six clusters as the
optimum number in the population (see Table 4).
Table 4: Results of clustering: six clusters
id_
client
area
pay
roll
balance
id_
cluster
93036 Rest of World 0 -959 1
60932 Rest of World 0 1 1
65940 Rest of World 0 35 1
07788 Madrid 0 10 4
87992 Madrid 0 241 4
67476 Madrid 1 1 2
44596 Madrid 1 16 2
14160 Madrid 1 141 2
11281 Madrid 1 353 2
65532 Madrid 1 631 2
74188 Madrid 1 965 2
18096 Barcelona 0 -36 5
45700 Barcelona 0 0 5
21184 Barcelona 0 5 5
10427 Barcelona 0 9 5
49867 Barcelona 1 0 6
01384 Barcelona 1 7 6
50392 Barcelona 1 1580 3
55689 Barcelona 1 1831 3
87752 Barcelona 1 1989 3
23952 Barcelona 1 2011 3
5 CONCLUSIONS
dmFSQL Server has been extended to handling of
different types of data (Carrasco 2002) and used as a
useful tool for certain Data Mining process
(Carrasco 1999, Carrasco 2001, Carrasco 2002) and
other applications (Galindo 1999). Now we have
applied dmFSQL for the clustering problem. Besides
the specific requirements of the clustering problem,
the prototype has been designed considering the
above-mentioned desirable functionalities of Data
Mining systems:
- Handling of Different Types of Data: The
possibility of combination any type of data for the
clustering process is considered novel in the
implementations of systems of this type.
- Mining Information from Different Sources of
Data: DAPHNE is very flexible when managing data
of different DBMS.
ICEIS 2005 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
140

- Efficiency and Interactive Mining Knowledge:
The prototype has been designed to be interactive
with the user and to give the answer in real time in
order to obtain the wanted population's partition.
- Accuracy: The use of the classic method of
Benzécri to obtain the hierarchy of parts has
guaranteed the goodness of such a partition. In
addition, the procedure to obtain a good partition
based on fuzzy sets has given excellent results
during the tests.
- Friendly Interface: The interface of DAPHNE is
graphic and completely user guided. Like-wise, the
prototype includes a meta-database, in such a way
that the management of a clustering project can
become quick and easy for the user.
Regarding future works:
- we will show a theoretical study of the
properties of the new similarity functions
incorporated in this work (combining fuzzy set
theory, classical distance functions, etc.) and
how imply the clustering process;
- we will specify an extension of dmFSQL
language that includes clustering clausules;
- we will integrate DAPHNE functionalities into
dmFSQL Server.
REFERENCES
J.P. Benzécri et coll, 1976. L'analyse des données; Tomo
I: La Taxinomie; Tomo II: L'analyse des
correspondences. Paris, Dunod.
R.A. Carrasco, J. Galindo, M.A. Vila, J.M. Medina, 1999.
Clustering and Fuzzy Classification in a Financial
Data Mining Environment. 3rd International ICSC
Symposium on Soft Computing, SOCO'99, pp. 713-
720, Genova (Italy), June 1999.
R.A. Carrasco, J. Galindo, A. Vila, 2001. Using Artificial
Neural Network to Define Fuzzy Comparators in
FSQL with the Criterion of some Decision-Maker. In
Bio-inspired applications of connectionism.-2001, eds.
J. Mira and A. Prieto, Lecture Notes in Computer
Science (LNCS) 2085, pp. 587-594. Ed. Springer-
Verlag, 2001, ISBN: 3-540-42237-4.
R.A. Carrasco, M.A. Vila, J. Galindo, 2002. FSQL: a
Flexible Query Language for Data Mining. In
Enterprise Information Systems IV, eds. M. Piattini, J.
Filipe and J. Braz, pp. 68-74. Ed. Kluwer Academic
Publishers, 2002, ISBN: 1-4020-1086-9.
M. Chen, J. Han, P.S. Yu, 1996. Data Mining: An
overview from a Data Base Perspective. IEEE
Transac. On Knowledge and Data Engineering, Vol 8-
6 pp. 866-883.
M. Delgado, A.F. Gómez-Skarmeta, A. Vila, 1996. On the
Use of Hierarchical Clustering. In Fuzzy Modelling.
International Journal of Approximate Reasoning, 14,
pp. 237-257.
W.J. Frawley, G. Piatetsky-Shapiro, C.J. Matheus, 1991.
Knowledge Discovery in Databases: An Overview. In
G. Piatetsky-Shapiro, W.J. Frawley eds. Knowledge
Discovery in Databases pp. 1-31, The AAAI Press.
J. Galindo, J.M. Medina, O. Pons, J.C. Cubero, 1998. A
Server for Fuzzy SQL Queries. In Flexible Query
Answering Systems, eds. T. Andreasen, H.
Christiansen and H.L. Larsen, Lecture Notes in
Artificial Intelligence (LNAI) 1495, pp. 164-174. Ed.
Springer.
J. Galindo, J.M. Medina, A. Vila, O. Pons, 1998. Fuzzy
Comparators for Flexible Queries to Databases.
Iberoamerican Conference on Artificial Intelligence,
IBERAMIA'98, pp. 29-41, Lisbon (Portugal), October
1998.
J. Galindo, J.M. Medina, J.C. Cubero, O. Pons, 1999.
Management of an Estate Agency Allowing Fuzzy
Data and Flexible Queries. EUSFLAT-ESTYLF Joint
Conference, pp. 485-488, Palma de Mallorca (Spain),
September 1999.
M.J. Martín-Bautista, M.A. Vila, 1998. Applying Genetic
Algorithms to the Feature Selection Problem in
Information Retrieval. In Flexible Query Answering
Systems, eds. T. Andreasen, H. Christiansen and H.L.
Larsen, Lecture Notes in Artificial Intelligence
(LNAI) 1495, pp. 272-281. Ed. Springer.
M.J. Quinn, 2003. Parallel Programming in C with MPI
and OpenMP. McGraw-Hill.
F.E. Petry, 1996. Fuzzy Databases: Principles and
Application (with chapter contribution by Patrick
Bosc). International Series in Intelligent Technologies.
Ed. H.-J. Zimmermann. Kluwer Academic Publishers
(KAP).
M.A. Vila, 1979. Nota sobre el cálculo de particiones
óptimas obtenidas a partir de una clasificación con
jerárquica. Actas de la XI Reunión Nacional de I.O.,
Sevilla, España.
USING dmFSQL FOR FINANCIAL CLUSTERING
141
