
NONPARAMETRIC ANALYSIS OF SOFTWARE RELIABILITY
Revealing the Nature of Software Failure Dataseries
Andreas S. Andreou, Constantinos Leonidou
Department of Computer Science, University of Cyprus,
75 Kallipoleos Str., P.O.Box 20537, CY1678, Nicosia, Cyprus
Keywords: software failure, reliability, nonparametric analysis, antipersistence
Abstract: Software reliability is directly related to the number and time of occurrence of software failures. Thus, if we
were able to reveal and characterize the behavior of the evolution of actual software failures over time then
we could possibly build more accurate models for estimating and predicting software reliability. This paper
focuses on the study of the nature of empirical software failure data via a nonparametric statistical
framework. Six different time-series data expressing times between successive software failures were
investigated and a random behavior was detected with evidences favoring a pink noise explanation.
1 INTRODUCTION
System reliability is one of the major components
identified by the ISO9126 standard for assessing the
overall quality of software. More specifically,
software reliability can be evaluated on the
following factors:
• Maturity: Attributes of software that bear on
the frequency of failure by faults in the
software (
ISO/IEC 9126-1:2001)
• Fault tolerance: Attributes of software that
bear on its ability to maintain a specified level
of performance in cases of software faults or
of infringement of its specified interface
(
ISO/IEC 9126-1:2001)
• Crash frequency: The number of the system
crashes per unit of time
• Recoverability: Attributes of software that
bear on the capability to re-establish its level
of performance and recover the data directly
affected in case of a failure and on the time
and effort needed for it (
ISO/IEC 9126-1:2001)
The standard definition of reliability for software
is th
e probability of normal execution without failure
for a specified interval of time (Musa, 1999; Musa,
Iannino and Okumoto, 1987). Going a step further
we can state that reliability varies with execution
time and grows as faults underlying the occurred
failures are uncovered and corrected. Therefore,
measuring and studying quantities related to
software failure can lead to improved reliability and
customer satisfaction. There are four general ways
(quantities) to characterize (measure) failure
occurrences (Musa, 1999):
• Time of failure
• Time interval between failures
• Cumulative failures experienced up to a given
time t
i
• Failures experienced in a time interval t
i
The majority of recent research studies focus on
so
ftware reliability assessment or prediction using
the failure-related metrics mentioned above (e.g.
Patra, 2003; Tamura, Yamada and Kimura, 2003),
with very few exceptions that experiment with other
alternatives, like Fault Injection Theory (e.g. Voas
and Schneidewind, 2003), Genericity (Schobel-
Theuer, 2003), etc.
As Musa points out (Musa, 1999), the quantities
of fai
lure occurrences are random variables in the
sense that we do not know their values in a certain
time interval with certainty, or that we cannot
predict their exact values. This randomness, though,
does not imply any specific probability distribution
(e.g. uniform) and it is sourced on one hand by the
complex and unpredictable process of human errors
introduced when designing and programming, and
on the other by the unpredictable conditions of
program execution. In addition, the behavior of
software is affected by so many factors that a
deterministic model is impractical to catch.
138
S. Andreou A. and Leonidou C. (2005).
NONPARAMETRIC ANALYSIS OF SOFTWARE RELIABILITY Revealing the Nature of Software Failure Dataseries.
In Proceedings of the Seventh International Conference on Enterprise Information Systems, pages 138-145
DOI: 10.5220/0002517601380145
Copyright
c
SciTePress

The aim of this paper is to study the nature and
structure of software failure data using a set of
empirical software failure dataseries and a robust
nonparametric statistical method. The ReScaled
range (R/S) analysis, originated by Hurst (Hurst,
1956), looks deep in a time-series dataset and
provides strong evidences of either an underlying
deterministic structure, or a random behavior. In the
former case it can define the time pattern of the
deterministic behavior, while in the latter it reveals
the nature of randomness (i.e. the colour of noise).
The rest of the paper is organized as follows:
Section 2 outlines the basic concepts of the
nonparametric framework used to analyse the
available datasets. Section 3 describes briefly the six
software failure time-series data used and provides a
short statistical profile for the data involved. Section
4 concentrates on the empirical evidence that results
from the application of R/S analysis on the different
software projects failure data. In addition, this
section presents our attempt to investigate through
R/S Analysis the nature of software failure data
produced by two well-known and widely used
Software Reliability Growth Models, namely the
Musa Basic model and the logarithmic Poisson
Musa-Okumoto execution time model, and
compares results with those derived using the
empirically collected data. Finally, section 5 sums
up the empirical findings, draws the concluding
remarks and suggests future research steps.
2 THE R/S ANALYSIS
Technically, the origins of R/S analysis are related to
the “T to the one-half rule”, that is, to the formula
describing the Brownian motion (B.M.):
R = T
0.5
(1)
where R is the distance covered by a random particle
suspended in a fluid and T a time index. It is obvious
that (1) shows how R is scaling with time T in the
case of a random system, and this scaling is given by
the slope of the log(R) vs. log(T) plot, which is equal
to 0.5. Yet, when a system or a time series is not
independent (i.e. not a random B.M.), (1) cannot be
applied, so Hurst gave the following generalisation
of (1) which can be used in this case:
(R/S)
n
= c n
H
(2)
where (R/S)
n
is the ReScaled range statistic
measured over a time index n, c is a constant and H
the Hurst Exponent, which shows how the R/S
statistic is scaling with time.
The objective of the R/S method is to estimate
the Hurst exponent, which, as we shall see, can
characterise a time series. This can be done by
transforming (2) to:
log (R/S)
n
= log(c) + H log(n) (3)
and H can be estimated as the slope of the log/log
plot of (R/S)
n
vs. n.
Given a time series {X
t
: t=1,...,N}, the R/S
statistic can be defined as the range of cumulative
deviations from the mean of the series, rescaled by
the standard deviation. The analytical procedure to
estimate the (R/S)
n
values, as well as the Hurst
exponent by applying (3), is described in the
following steps :
Step 1: The time period spanned by the time series
of length N, is divided into m contiguous sub-periods
of length n such that mn = N. The elements in each
sub-period X
i,j
have two subscripts, the first (i=1,..,n)
to denote the number of elements in each sub-period
and the second (j=1,...,m) to denote the sub-period
index. For each sub-period j the R/S statistic is
calculated, as:
⎥
⎦
⎤
⎢
⎣
⎡
−−−=
⎟
⎠
⎞
⎜
⎝
⎛
∑∑
==
≤≤
≤≤
−
k
i
k
i
jij
nk
jij
nk
j
j
XXXXs
S
R
11
1
1
1
)(min)(max
(4)
where s
j
is the standard deviation for each sub-
period.
In (4), the k deviations from the mean of the sub-
period have zero mean; hence the last value of the
cumulative deviations for each sub-period will
always be zero. Due to this, the maximum value of
the cumulative deviations will always be greater or
equal to zero, while the minimum value will always
be less or equal to zero. Hence, the range value (the
bracketed term in (4)), will always be non-negative.
Normalizing (rescaling) the range is important since
it permits diverse phenomena and time periods to be
compared, which means that R/S analysis can
describe time series with no characteristic scale.
Step 2: The (R/S)
n
, which is the R/S statistic for time
length n, is given by the average of the (R/S)
j
values
for all the m contiguous sub-periods with length n,
as :
∑
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
m
j
jn
S
R
mS
R
1
1
(5)
Step 3: Equation (5) gives the R/S value, which
corresponds to a certain time interval of length n. In
order to apply equation (3), steps 1 and 2 are
repeated by increasing n to the next integer value,
until n = N/2, since, at least two sub-periods are
needed, to avoid bias.
From the above procedure it becomes obvious that
the time dimension is included in the R/S analysis by
examining whether the range of the cumulative
deviations depends on the length of time used for the
measurement. Once (5) is evaluated for different n
NONPARAMETRIC ANALYSIS OF SOFTWARE RELIABILITY: Revealing the Nature of Software Failure Dataseries
139

periods, the Hurst exponent can be estimated
through an ordinary least square regression from (3).
The Hurst exponent takes values from 0 to 1
(0≤H≤1). Gaussian random walks, or, more
generally, independent processes, give H = 0.5. If
0.5 ≤ H ≤1, positive dependence is indicated, and the
series is called persistent or trend reinforcing, and in
terms of equation (1), the system covers more
distance than a random one. In this case the series is
characterised by a long memory process with no
characteristic time scale. The lack of characteristic
time scale (scale invariance) and the existence of a
power law (the log/log plot), are the key
characteristics of a fractal series. If 0 ≤H ≤0.5,
negative dependence is indicated, yielding anti-
persistent or mean-reverting behavior
1
. In terms of
equation (1), the system covers less distance than a
random series, which means that it reverses itself
more frequently than a random process.
A Hurst exponent different from 0.5 may
characterise a series as fractal. However a fractal
series might be the output of different kinds of
systems. A “pure” Hurst process is a fractional
Brownian motion (Mandelbrot and Wallis, 1969),
also known as biased random walk or fractal noise
or coloured noise, that is, a random series the bias of
which can change abruptly but randomly in direction
or magnitude.
A problem, though, that must be dealt is the
sensitivity of R/S analysis to short-term dependence,
which can lead to unreliable results (Aydogan and
Booth, 1988; Booth and Koveos, 1983; Lo, 1991).
Peters (Peters, 1994) shows that Autoregressive
(AR), Moving Average (MA) and mixed ARMA
processes exhibit Hurst effects, but once short-term
memory is filtered out by an AR(1) specification,
these effects cease to exist. On the contrary, ARCH
and GARCH models do not exhibit long term
memory and persistence effects at all. Hence, a
series should be pre-filtered for short-term linear
dependence before applying the R/S analysis. In our
analysis, we use partial autocorrelograms and
Schwartz´s information criterion to indicate the best-
fit time series linear model to our data.
3 SOFTWARE FAILURE DATA
Before moving to applying R/S Analysis on the
available software failure datasets, let us examine
some basic features of the data: Six different
1
Only if the system under study is assumed to have a
stable mean
datasets were used in this paper, which were
collected throughout the mid 1970s by John Musa,
representing projects from a variety of applications
including real time command and control, word
processing, commercial, and military applications
(DFC, www.dacs.dtic.mil): Project 5 (831 total
samples), SS1B (375 total samples), SS3 (278 total
samples), SS1C (277 total samples), SS4 (196 total
samples) and SS2 (192 total samples).
R/S analysis can be applied only on a
transformation of the original data samples which
produces the so-called return series eliminating any
trend present. This transformation is the following:
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
−1
log
t
t
t
S
S
r
(6)
where S
t
and S
t-1
are the failure samples (more
specifically, the elapsed times form the previous
failure measured in seconds) at times (t) and (t-1)
respectively (discrete sample number) and r
t
is the
estimated return sample.
As mentioned in the previous section, in order to
remove the short-term memory all return series were
filtered with an AR(1) model. A short statistical
profile is depicted in Table 1, where one can easily
discern that the series under study present slight
differences from the normal distribution: Left
skewness is evident for all data series, while, as
regards kurtosis, Project 5 samples present
leptokurtosis with the rest series being less
concentrated around the mean compared to the
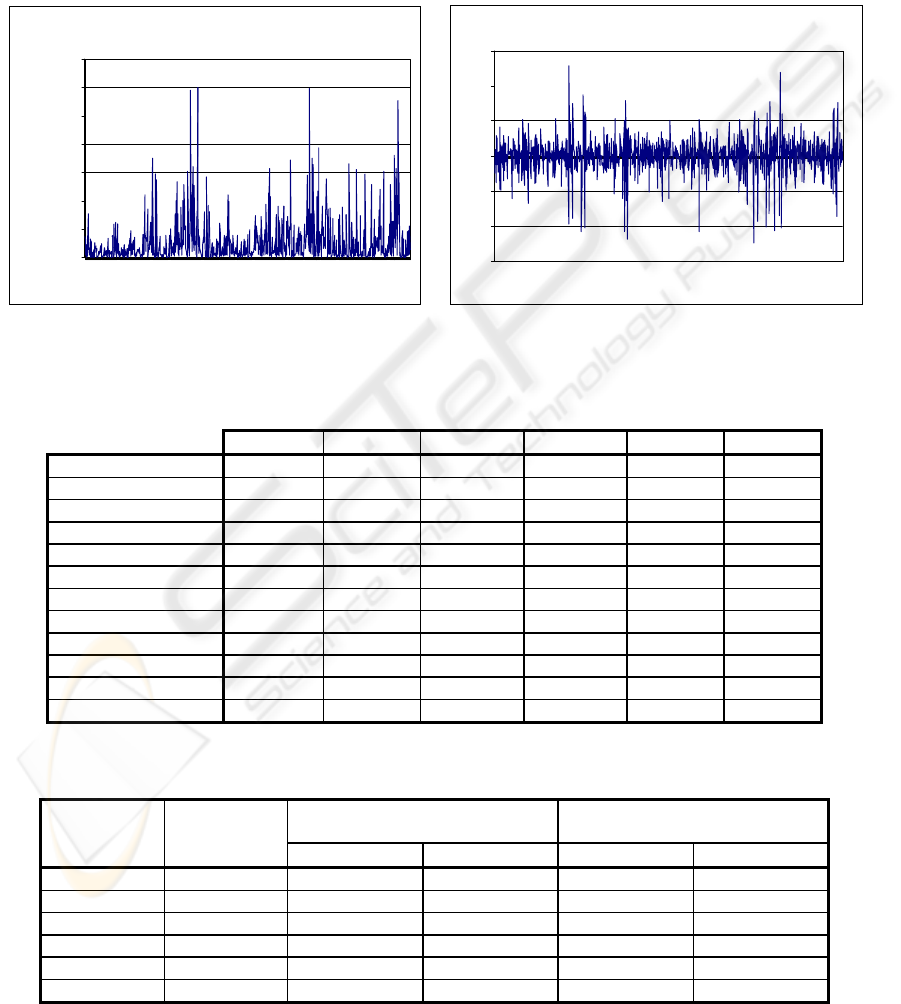
normal distribution. Figure 1 plots the data samples
belonging to Project 5, with the left figure showing
the evolution of failures according to the elapsed
time and the right figure presenting the de-trended
return series. The rest of the datasets present a
similar graphical representation, thus their figures
were omitted due to space limitations.
The statistical profile of the dataseries given
above suggests a general resemblance with the
normal (Gaussian random) distribution, but slight
differences were also observed. The main questions,
though, remain: What is the actual nature of this
data? Is there a random component in the behavior
of these series? The answers will be provided by
closely examining the results derived from the
application of R/S Analysis described in the next
section.
ICEIS 2005 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
140
4 EMPIRICAL EVIDENCE
These Hurst exponent values indicate anti-
persistency, that is, all return series present negative
dependence or antipersistence, yielding a mean-
reverting behavior since the data fluctuate around a
reasonably stable mean (no trend or consistent
pattern of growth). In terms of equation (1), each of
the six systems covers less distance than a random
series, which means that it reverses itself more
frequently than a random process.
4.1 R/S Analysis Results on Software
Reliability Data Series
The results of R/S analysis on the six failure return
series are listed in Table 2. The Hurst exponent
estimated has a low value ranging from 0.27 (Project
5 dataset) to 0.37 (SS1C dataset).
AR(1)-filtered returns for the "Pro
j
ect 5" software
failure dataset
-6
-4
-2
0
2
4
6
1 61 121 181 241 301 361 421 481 541 601 661 721 781
sample
return
Time intervals between successive software
failures for the "Project 5" dataset
0
50000
100000
150000
200000
250000
300000
350000
1 61 121 181 241 301 361 421 481 541 601 661 721 781
failure number
seconds
(a) (b)
Figure 1: Project 5 sample series: (a) Time intervals between successive failures (b) AR(1)
Table 1: Statistical description of the six software failure returns series data (AR(1)-filtered samples)
Project 5 SS1B SS3 SS1C SS4 SS2
Sample size
829 373 276 275 194 191
Average
5.55E-18 2.97E-18 -1.20E-18 -5.85E-18 1.54E-17 3.95E-17
Median
0.024 0.073 0.075 0.084 0.121 -0.027
Variance
1.150 0.871 1.936 0.988 1.421 1.176
Standard deviation
1.072 0.933 1.391 0.993 1.192 1.084
Minimum
-4.963 -3.120 -5.056 -3.094 -4.127 -2.634
Maximum
5.165 2.879 3.470 4.786 2.832 3.268
Range
10.129 6.000 8.526 7.881 6.960 5.902
Lower quartile
-0.479 -0.536 -0.761 -0.473 -0.699 -0.671
Upper quartile
0.597 0.619 0.942 0.563 0.823 0.712
Skewness
-0.616 -0.263 -0.315 -0.034 -0.432 -0.131
Kurtosis
4.082 0.457 0.180 2.327 0.713 -0.019
Table 2: Hurst estimates and test of significance against two random alternatives for the AR(1)-filtered
returns series of the six different Musa’s software failure datasets
IID-null
Hypothesis
Gaussian-null
Hypothesis
Dataset
Hurst
Exponent
Mean Hurst Significance Mean Hurst Significance
Project5 0.27 0.56 0.1% 0.56 0.1%
SS1B 0.31 0.58 0.1% 0.58 0.1%
SS3 0.28 0.59 0.1% 0.60 0.1%
SS1C 0.37 0.59 0.1% 0.59 0.1%
SS4 0.33 0.60 0.1% 0.60 0.1%
SS2 0.33 0.60 0.1% 0.60 0.1%
NONPARAMETRIC ANALYSIS OF SOFTWARE RELIABILITY: Revealing the Nature of Software Failure Dataseries
141

A significant problem of R/S analysis is the
eva
lts obtained using the R/S
ana
m null, the H
est against the iid null, the same procedure is
tion of the R/S analysis results was
per
resembles the one observed for random, non-white
laws, which essentially is a function of
freq
b is the spectral component and H the
Hur t. T e can relate pi
to a
can conclude
tha
nalysis and Software
ystem
Havi ults thus far and the evidences
suggesting a pink noise explanation for the behavior
luation of the H exponent from a statistical point
of view. Specifically, we should be able to assess
whether an H value is statistically significant
compared to a random null, i.e. to the H exponent
exhibited by an independent random system. Peters
(1994) shows that under the Gaussian null, a
modification of a formula developed by Anis and
Lloyd (1976) allows for hypothesis testing by
computing E(R/S)
n
and E(H), the expected variance
of which will depend only on the total sample size
N, as Var(H)=1/N. However, if the null is still iid
randomness but not Gaussianity, the formal
hypothesis testing is not possible. To overcome this
problem we used bootstrapping (Efron, 1979) to
assess the statistical significance of the H exponents
of our series, against both the Gaussian and the iid
random null hypotheses.
The validity of the resu
lysis may be assessed as follows:
(A) To test against the Gaussian rando
exponent from 5000 random shuffles of a Gaussian
random surrogate, having the same length, mean and
variance with our return series is calculated and
compared to the test statistic i.e. the actual H
exponent of our series. Since the actual H statistic
was found to be lower than 0.5 and anti-persistence
is possible, the null can be formed as: H
0
: H = H
G
and the alternative is
H
1
: H < H
G
. In this case, the
significance level of the test is constructed as the
frequency with which the pseudostatistic H
G
is
smaller than or equal to the actual statistic and the
null is rejected if the significance level is smaller
than the conventional rejection levels of 1%, 2.5%
or 5%.
(B) To t
followed but this time we randomise the return
series tested to produce 5000 iid random samples
having the same length and distributional
characteristics as the original series. In this case,
rejection of the null means that the actual H
exponent calculated from the original series is
significantly smaller from the one calculated from an
iid random series. Hence, this is also a test for non-
iid-ness.
Valida
formed as described above, with both tests being
applied to the available dataseries. As Table 2
shows, both hypotheses are rejected since the
significance level of the test in both cases was lower
than 1%. This means that our Hurst estimates are
statistically significant against both the Gaussian and
the iid-null hypotheses suggesting an underlying
structure that deviates from normal distribution and
noise.
Fractional noise scales according to inverse
power
uency f, and follows the form f
-b
. This is a
typical characteristic of fractals, which have power
spectra that follows the inverse power law as a result
of the self-similar nature of the system (Peters,
1994). For white noise (Gaussian, random process)
b = 0, that is, the power spectra is not related to
frequency. There is no scaling law for white noise.
When white noise is integrated, then b = 2, the
power spectra for brown noise. If 0 < b < 2 we have
pink noise, while when b > 2 there is black noise.
Mandelbrot and Van Ness (Mandelbrot and Van
Ness, 1968) postulated, and recently Flandrin
(Flandrin, 1989) rigorously defined, the following
equation that relates fractional noises with the Hurst
exponent:
b = 2H + 1 (7)
where
st exponen herefore, w nk noise
ntipersistence: H < 0.50, 1 ≥ b > 2.
According to the foregoing notions, and based
on the results of the R/S analysis, we
t the six software failure data series are random in
nature, thus confirming the findings and supporting
the arguments of various researchers (Musa, 1999;
Musa and Iannino, 1990). Moving a step forward,
we may state that the main conclusion drawn is that
software failure empirical behavior resembles that of
pink noise.
4.2 R/S A
Reliability Growth Models S
Variables
ng in mind the res
of the empirical software failure data, we will
attempt to study the nature of the data produced by
known Software Reliability Growth Models
(SRGM) and compare results. Several studies (Dale,
1982; Ramamoorthy and Bastani, 1982; Farr, 1996;
Jones 1991) report the superiority of the Musa Basic
(MB) and the logarithmic Poisson Musa-Okumoto
(MO) execution time models (Musa, 1975; Musa
and Okumoto, 1984) over a variety of SRGM widely
applied to different actual projects and computer
programs. Therefore, we decided to use those two
models to produce new software failure time
samples and apply R/S analysis to investigate the
nature of the produced dataseries, and hence the type
ICEIS 2005 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
142

of software failure behavior each model is capable to
capture. Let M(t) represent the number of failures of
the particular software package by time t, (t≥0). It is
clear that M(0)=0. M(t) cannot be easily calculated
because it corresponds to a physical quantity and can
only be measured as the software is tested. Software
Reliability Growth Models are trying to model the
behavior of M(t) with the statistical function µ(t).
The mean value function µ(t) of a SRGM represents
the number of failures expected to occur up to time
moment t, (t≥0):
Ntct )()( =
µ
(8)
where c(t) is the time variant test coverag
func N is the number
hav
e
tion and of faults expected to
e been exposed at full coverage. This is
distinguished from the expected number of faults to
be detected after infinite testing time, perfect testing
and fault detection coverage, which can be denoted
as
N
ˆ
. Equations (9) and (10) describe the test
coverage function for the MB and MO models
respectively:
MB :
fKBt
etc
−
−=1)(
(9)
MO :
)1ln()( ttc
φ
+
=
(10)
where φ is e s the so-the failure rate p r fault, K i
call sure ratio, B is a fault r
fac
ed fault expo eduction
tor and f can be calculated as the average object
instruction execution rate of the computer r, divided
by the number of source code instructions of the
application under testing I
S
, times the average
number of object instructions per source code
instruction, Q
x
(Musa, 1999):
xS
QI
r
f =
(11)
Both M(t) q nc he form and µ(t) are se ue es of t
0,1,2, … with M(0)=0 and µ(0)=0. Assuming that as
t
ime t as t app
positive variable i, (i=0,1,2...). Thus, we
hav
Su g c(t
i
) in (9) and (10) and solving for t
i
we
e:
approaches infinity µ(t) becomes a good
approximation of M(t) (the number of failures that
has been realized up to time t) we will have µ(t)
taking by definition integer positive values (since
µ(t) corresponds to the expected number of failures
experienced by time t; hence
[]
K,2,1,0)( ∈t
µ
). Both
SRGMs (MB and MO) converge to the number of
failures being realized up to t roaches
infinity is generally acceptable. Therefore, our
assumption that M(t) will be approached by µ(t) as t
approaches infinity. But µ(t), which characterizes a
SRGM, is given as a model property, thus we should
try to reverse engineer the process of failure
occurrence and artificially reproduce the “ failure
occurrences”. The failure reproduction process is as
follows:
First we replace µ(t) in equation (8) with an
integer
e:
i=c(t
i
)N (12)
bstitutin
hav
MB:
⎟
⎞
⎜
⎛
−−=⇔−=
−
i
tNei
fKBt
i
1ln
1
)1(
(13)
⎠⎝
NfKB
i
MO:
⎟
⎠
⎞
⎜
⎝
⎛
−=⇔+= 1
1
)1ln(
N
i
ii
etNti
ϕ
φ
me variable t
i
represents discrete fa
moments, i.e. the time elapsed from the start of this
pro
(14)
Ti
ilure time
cess (t
0
for i=0) until the occurrence of the i
th
failure (t
1
for i=1, t
2
for i=2 etc.).
Consequently we can calculate times between
successive failures as:
escribed above, we
duc artific es d ta via e
13
failure dataseries were thus
g
5 CONCLUSIONS – DISCUSSION
The nature of empirical software reliability time
series data was investigated in this paper using a
∆t
i
= t
i
- t
i-1
. (15)
Following the analysis d
repro ed ial failure tim a quations
to 15, for which we used the following parameter
values suggested by Musa (1975, 1999) and the
Defense Software Collaboration (DFC,
www.dacs.dtic.mil):
φ = 7.8 E-8, f = 7.4 E-8, K = 4.2 E-7, B= 0.955
Two new software
enerated, with their size being equal to that of
Project 5 (829 samples). R/S analysis was then
applied on the AR(1)-filtered returns of the
artificially reproduced series. The Hurst exponent
estimations indicate that the MB-based reproduced
series exhibit long-memory or persistent effects
(H=0.9), while the corresponding MO-based sample
data is characterized as antipersistent (H=0.2). These
findings are very interesting considering the fact that
they suggest a strong diversification between two
models that are both used as software reliability
growth estimators, and hence as software failure
predictors. The similar antipersistent
characterization of the six software failure dataseries
under study and the MO-based generated data is also
consistent with the findings of other researchers who
report the superiority of the MO model in actual
software projects. It is therefore natural that this
model proved to be more successful compared to the
rest of the SRGMs simply because its underlying
modeling nature is similar to the behavior observed
with actual empirical data.
NONPARAMETRIC ANALYSIS OF SOFTWARE RELIABILITY: Revealing the Nature of Software Failure Dataseries
143

robust nonparametric statistical framework called
ReScaled range (R/S) analysis. This type of analysis
ing process should play a central role in the
pla
ast five years. We are trying to
bui
is able to detect the presence (or absence) of long-
term dependence, thus characterizing the system
under study as persistent / deterministic (or mean-
reverting / antipersistent).
The results of the R/S analysis on six different
software failure dataseries suggested a random
explanation, revealing strong antipersistent behavior.
The validity of these results was tested against the
Ga
ussian and iid-null hypotheses and both
alternatives were rejected with highly significant
statistical values. Our findings are consistent with
other reports in the international literature that
comment on the random nature of software failures
in terms of number and time of occurrence. Going a
step further and relating the values of the Hurst
exponent estimated via the R/S analysis with colored
noise, we concluded that the six series examined are
better described by a pink noise structure.
Two well known and successful software
reliability growth models, namely the Musa Basic
(MB) and the Musa-Okumoto (MO) logarithmic
model, were used to reproduce sample series of
tim
es between failures. The new series were also
tested with R/S analysis and found to be long-term
dependent in the case of the MB data and
antipersistent in the case of the MO series. The latter
finding justifies the superiority of the MO model
over a variety of other SRGM tested on a number of
actual projects: The MO model is ruled by the same
structure as the empirical software failure data (i.e.
mean reverting), thus it can capture the actual
behavior of software failures better.
The framework for statistical characterization of
empirical software failure data proposed by the
present work can assist towards the identification of
possible weaknesses in the assumptions of SRGMs
and
suggest the most suitable and accurate model to
be used for controlling the reliability level of the
software product under development.
One thing that remains to investigate, and this
will be the focus of our future work, is the high
value of the Hurst exponent for the MB series.
Chaotic systems have also Hurst exponents H > 0.5,
and
in chaotic terms long memory effects
correspond to sensitive dependence on initial
conditions. Actually, the latter property combined
with fractality characterises chaotic systems. Pure
chaotic processes have Hurst exponents close to 1.
Our future research will concentrate on employing
R/S analysis to detect the existence of cycles (i.e.
repeating patterns) in the MB series and will attempt
to characterise it in terms of periodicity: Cycles
detected can be periodic or non-periodic in the sense
that the system has no absolute frequency. Non-
periodic cycles can be further divided to statistical
cycles and chaotic cycles. Fractal noises exhibit
statistical cycles, i.e. cycles with no average cycle
length.
Software Reliability is cited by the majority of
users as the most important feature of software
products. Hence, the software reliability
engineer
nning and control of software development
activities (Musa, 1999) to ensure that product
reliability meets user needs, to reduce product costs
and to improve customer satisfaction. In this context,
it is quite important to record and study the time of
fault occurrences, their nature and the time spent on
correction, throughout the design and
implementation phases, as well as during testing
activities. This data can prove very useful when
trying to model the reliability behavior of the
software product being developed and it can also
play a central role to the empirical verification of
Software Reliability Growth Models (SRGMs).
With such data available it is easier to select suitable
reliability models for estimating the time at which
the software product will have reached a desirable
level of reliability, and/or to devise methods to
decrease that time. As we mentioned before, the
datasets used in this study were gathered by John
Musa around mid seventies. Although the datasets
are quite old, we believe that their analysis is a good
starting point for studying the behavior of software
failure occurrences.
Currently we are making efforts towards
gathering synchronous failure data, that is, data from
systems that have been developed and are in
operation during the l
ld a database with failure data from various
modern application domains and operating systems.
In our days, where most computer applications and
operating systems are multitasking and/or
distributed, it is very interesting to elaborate on how
to gather accurate failure data. This problem, the
definition of the right metrics to assess software
reliability, has a particular interest due to the fact
that software products nowadays include some new
and unique characteristics, such as distribute
computing, mobility and web accessibility /
immediacy. Once this reliability data gathering is
accomplished, we will be able to compare the
characteristics of modern reliability data with those
of the datasets developed by Musa in the 70ies, and
investigate whether the random nature of software
failure occurrences revealed by the R/S analysis
ICEIS 2005 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
144

holds true for modern software systems as well.
Furthermore, we will attempt to investigate whether
there is a relationship between the datasets used and
the results obtained, i.e. whether certain application
domains are more error prone than others.
REFERENCES
Anis, A.A. and Lloyd E.H., 1976. The Expected Value of
endent
iometrica 63, pp. 155-164.
Aydogan, K. and Booth, G., 1988. Are there long cycles in
Bo ment
Da ware Reliability Evaluation Methods,
De
the Adjusted Rescaled Hurst Range of Indep
Normal Summands. B
common stock returns? Southern Economic Journal
55, pp. 141-149.
oth, G.G. and Koveos, P.E., 1983. Employ
fluctuations: an R/S analysis. Journal of Regional
Science 23, pp. 19-31.
le, C.J., 1982. Soft
Report ST26750, British Aerospace.
fense Software Collaboration,
http://
www.dacs.dtic.mil/techs/baselines/reliability. html
Efron, B., 1979. Bootstrap methods: Another look at the
jack-knife. The Annals of Statistics 7,
pp. 1-26.
ility
Fla ctional
Hu in
Inte rganization for Standardization, 1991.
Ma
ents with fractional Gaussian noises. Part 1, 2,
Ma Fractional
Mu tware Reliability. In
Mu re Reliability and its
Musa, J.D., Iannino, A., Okumoto, K., 1987. Software
national Conference on
Pat
ftware Reliability
Pet
ering 8(4), pp. 354-370.
on Software
Tam
networks for distributed development
Vo
IEEE
Farr, W., 1996. Software Reliability Modeling Survey. In
M. Lyu (ed.) Handbook of Software Reliab
Engineering, McGraw-Hill, New York, pp. 71-117.
ndrin, P., 1989. On the Spectrum of Fra
Brownian Motions, IEEE Transactions on Information
Theory 35.
rst, H.E, 1956. Methods of using long-term storage
reservoirs. Proceedings of the Institute of Civil
Engineers 1, pp. 519-543.
rnational O
ISO/IEC 9126 - Information Technology, Software
Product Evaluation, Quality, Characteristics and
Guidelines for their Use.
Jones, W.D., 1991. Reliability Models for Very Large
Software Systems in Industry, 2
nd
International
Symposium on Software Reliability Engineering, pp.
35-42.
Lo, A.W., 1991. Long term memory in stock market
prices. Econometrica 59, pp. 1279-1313.
ndelbrot, B. and Wallis, J., 1969. Computer
experim
3. Water Resources Research 5.
ndelbrot, B. and van Ness, J.W., 1968.
Brownian Motions, Fractional Noises and
Applications, SIAM Review 10.
sa, J.D., Iannino, A., 1990. Sof
Marshall Yvotis (ed.) Advances in Computers 30, pp.
85-170, Academic Press, San Diego.
sa, J.D., 1975. A Theory of Softwa
Application, IEEE Trans. Software Eng. 1(3), pp. 312-
327.
Musa, J., 1999. Software Reliability Engineering,
McGraw-Hill, New York.
Reliability - Measurement, Prediction, Application,
McGraw-Hill, New York.
Musa, J.D., Okumoto, K., 1984. A Logarithmic Poisson
Execution Time model for Software Reliability
Measurement, 7
th
Inter
Software Engineering, pp. 230-238.
ra, S., 2003. A neural network approach for long-term
software MTTF prediction. In Fast abstracts of the 14
th
IEEE International Symposium on So
Engineering (ISSRE2003), Chillarege Press.
ers, E., 1994. Fractal market analysis: applying chaos
theory to investment and economics. New York: John
Wiley & Sons.
Ramamoorthy, C.V., Bastani, F.B., 1982. Software
Reliability – Status and Perspectives, IEEE Trans. On
Software Engine
Schobel-Theurer, T., 2003. Increasing software reliability
through the use of Genericity. In Fast abstracts of the
14
th
IEEE International Symposium
Reliability Engineering (ISSRE2003), Chillarege
Press.
ura, Y., Yamada, S. and Kimura, M., 2003. A
software reliability assessment method based on
neural
environment. Electronics and Communications in
Japan, Part 3, Vol. 86, No. 11, pp. 1236-1243.
as, J. and Schneidewind, N., 2003. Marrying software
Fault Injection Technology with Software Reliability
Growth Models. In Fast abstracts of the 14
th
International Symposium on Software Reliability
Engineering (ISSRE2003), Chillarege Press.
NONPARAMETRIC ANALYSIS OF SOFTWARE RELIABILITY: Revealing the Nature of Software Failure Dataseries
145
