MULTI-AGENT SYSTEM FORMAL MODEL BASED ON

NEGOTIATION AXIOM SYSTEM OF TEMPORAL LOGIC

Xia Youming , Yin Hongli and Zhao Lihong

School of Computer Science and Information Technology,

Yunnan Normal University,Kunming , P.R.China

Keywords: Negotiation Axiom, Semantic Frame, Multi-Agent System, Negotiation Reasoning Logic, Temporal Logic

Abstract: In this paper we describe the formal semantic frame and introduce the formal language L

to express the

time and the ability and right of an agent on selecting action and negotiation process in a Multi-Agent

System, the change of the right over time, the free action of an agent and the time need by a agent to

complete an action. Based on the above, the independent negotiation system has been further complete. In

this paper, it is also addressed that the axiom system is rational, validate and negotiation reasoning logic is

soundness, completeness and consistent.

1 INTRODUTION

The research of agent technique is a new field of

software design and realization，and has caught

people’s attention for years, especially in distribution

and open Internet software developing field. As the

mature of technique and more complex application

problems being put forward, the requirements of

multi-agent system based on peer-to-peer mode

communication have become more and more urgent.

The research of the key technology of MAS’s design

and effective implement has been carried out for

many years in the field of distribution artificial

intelligence.

For MAS, besides the consideration of the

representation and formalization of consciousness

attitude concerning individual agent, it must

consider the alternation of multi agents, the

consciousness attitude that is one of the important

portions of MAS theory research. As being able to

reason about other agents, consciousness attitude is

the main request that makes the agents to coexist,

compete and collaborate. The cooperation and

negotiation can be produced and accomplished

under the control of psychosis. Negotiation of MAS

include negotiation protocol, negotiation strategy

and negotiation disposal. The first part focus on

dealing with the intercommunication among agents,

and the second part has five basic types: one-part

giving in strategy, competitive strategy, cooperation

strategy, destroying strategy and delaying strategy.

This paper is based on Li Jing’s work, and add

temporal logic to complete negotiation between

independent agents by using linear temporal logic

describe right change to make contribution on letting

agents act more freely.

2 NEGOTIATION AXIOM

SYSTEM WITH TEMPORAL

LOGIC

The Negotiation Axiom System based on Capability

and Thought of MAS(Li Jing 03)is viewed as a

sequence of “Perceiving→Selecting

actions→Negotiating to resolve conflicts→Deciding

actions by arbitrage →Executing actions”.

In the TN system (the abbreviation of the

negotiation axiom system with temporal logic), the

primary work unit is spitted into many small units,

that allow agents behaviors to be asynchronous, that

is the starting point of negotiations and the other

actions taken by agents can be different, so a agent is

able to start a negotiation when there is another

agent is still executing an action; Further, when

some agents are executing actions, other agents keep

observing the environment, and then choose their

The work is supported by the Natural Science Foundation of Yunnan province under the grant No. 2003F0038M, the

Key Project of Yunnan Natural Science Foundation under the grant No. 04F00062, and the Province-Institute and

Province-Universit

Scientific and technolo

ical collaborative

ect of Yunnan Province

(

2004YX42

)

362

Youming X., Hongli Y. and Lihong Z. (2005).

MULTI-AGENT SYSTEM FORMAL MODEL BASED ON NEGOTIATION AXIOM SYSTEM OF TEMPORAL LOGIC.

In Proceedings of the Seventh International Conference on Enterprise Information Systems, pages 362-365

DOI: 10.5220/0002517503620365

 SciTePress

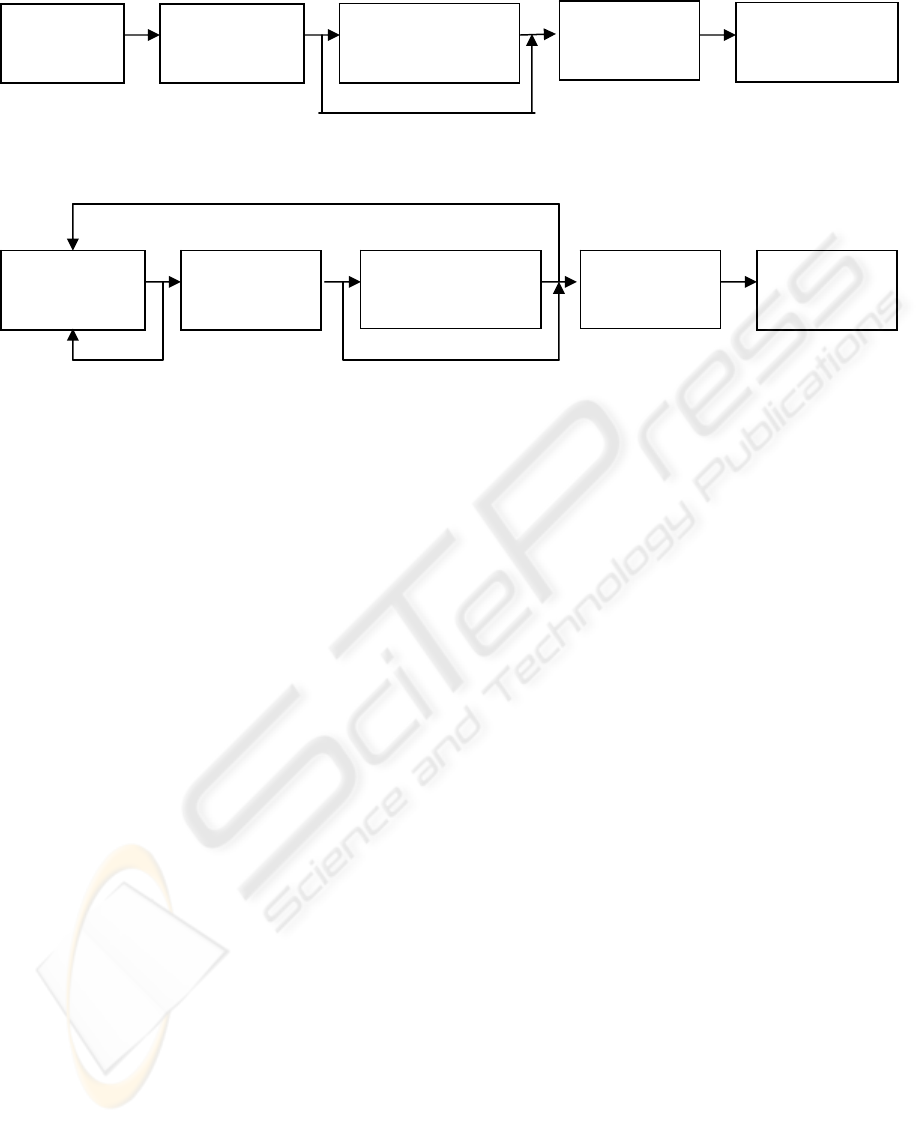
Perceiving

Selecting actions

Negotiating to resolve

conflicts

Deciding actions

by arbitrage

Executing actions

Figure 2: Interpretation of the negotiation axiom system with temporal logic

Perceiving

Selecting actions

Negotiating to resolve

conflicts

Deciding actions

by arbitrage

Executing actions

Figure 1: Interpretation of the negotiation axiom system based on capability and thought of MAS

next movements based on local states, power and

rights, that is the environment observations are

simultaneous.

In our work, the VSK-AF logic system is still

valid in the course of perceiving, but in the course of

selecting actions, negotiating to resolve conflicts,

deciding actions by arbitrage and executing actions,

we use the negotiation with temporal logic. In the

TN system，negotiation concurrence is allowed, and

all those negotiations may start at a different time

point, last for a different time period, end at a

different time point.

2.1 Semantic Frame

To discus the TN system we define the following

semantic frame:

T = {t

, t

,…, t

, …}: a set of time points;

Actions = {α

, α

,…}: a set of actions, which

consists of all actions involved in this system;

NS = {ns

, ns

,…}: a set of negotiation

strategies;

AS = {as

,as

,…}: a set of arbitrage strategies;

Message = a set of (i,α,w), Ag

select the

action α to execute the task w;

E = {e

, e

, …}: a set of the external

environment states;

S = {s

, s

, …}: a set of the Agents environment

states;

W = {w

, w

, …}: a set of tasks;

Environment: one of the two important parts

of the model, denoted as Env = <E, S, W, vis

, …,

vis

, acce

, …, acce

, Arbitrage, τ

, e

, s

= { l

, l

…}: the set of local state for Agent

;

Agents: one of the two important parts of the

model, denoted as Ag

=<L

, See

, Feel

, Th

, Ability

Power

, SelectAP

, Donetime

, Decide

, CR

, τ

, l

, Poss

Negotiation: denoted as N=<Ags, Isu, O, V

Ans, Time, Thread, Protocol>;

TN System: denoted as S=<Actions, NS, AS,

Env, Agents, N, PoS, SR, T>;

Global states for a TN system: denoted as

G={ε

, ε

, …};

The class of TN system: consists of all TN

system, denoted as S;

Run: A sequence ε

, ε

, …(enumerable) over G

represents the run of a TN system

The set of reachable states for TN system:

denoted as G

At the very beginning, L

is initialized as the initial

local state, E is initialized as the external state, and S

is initialized as the initial agent state, then each

agent start the first observation and use the vis (the

partition function of the external environment for

Agent

) and the acce

( the partition function of

the Agents environment for Agent

) to product a p

(the acknowledge of the external environment) and a

(the acknowledge of the agents environment),

thus the L

transfer to a new local state L

i+1

and we

get a initial global states for the TN system. With the

initial global states, each agent makes its own

selection according to the power and right they have

at this moment, on the contrary, a agent has no

power and right doing nothing till the next time

point comes, they start a new observation. Those

agents with power and right select an action and the

corresponding task, if there is no confliction among

those selected actions, the agent then execute the

selected action, transfer the environment states.

When they finish the execution start an observation

again. Once the conflictions occur, those agents

MULTI-AGENT SYSTEM FORMAL MODEL BASED ON NEGOTIATION AXIOM SYSTEM OF TEMPORAL

LOGIC

363

involved negotiate with each other till the

agreements are finally reached, and they act

according to the agreement to transfer the state of

the system. Till all problems are solved, the process

will be repeated.

2.2 Negotiation Logic in TN System

This section gives an overview of the formal

framework in which the model of negotiation will be

expressed in language L

TN.

The language expresses

the model of negotiation, and describes the system

information, which consists of two parts: the first

part—the language of VSK-AF logic, is used in the

course of perceiving ， to express the objective

phenomenon in multi-Agent systems, the

information that can be visited, learn or perceived by

a agent in the system, the second part—L

, is used

in the rest phases, to describe how the time, power,

and right effect the agent on the action selection and

negotiation, especially the change of the right during

the whole process.

In TN system, we introduce five temporal

operators: □(always)，◇(eventually)，○(next)，◆

(ever)，∪(until).

Given a set P of prepositional variables, set

Agents of agents, set Actions of actions, set W of

task, and for an action α∈ Actions has a set of

preconditions Pre(α), and a set of effects Eff(α), the

language L

is defined as below:

A list of predications as following:

Exu(Agi,α,w), Capable(Agi,α), R-Entitle (Agj,Agi,

α), NR-Entitle (Agj, Agi,α), Entitle(Agj,Agi,α),

Right(Agi,α), Done(Agi,α,w), Agree(Γ,ϕ), Bound

(Agi,agm), Commit (Agi, Agj, agm), Benefit(Agi,α),

Select(Agi,α,w), Collision(Agts,α,w), Negotiation

(Agts,α,w), DuringNegotiation (Agts, α, w), Join-

Negotiation(Agi,α,w), OverNegotiation(Agts,Agk,α,

w), Permit(Agi,Agj,Entitle(Agj,Agk,α)), Deprive

(Agi, Agj,α) and so on.

(the set of atomic propositions of L

consists of P and predications mentioned above.

Φ (the set of compound formula of L

1．True, False∈Φ, Φ

⊆Φ;

2．If ϕ

, ϕ

∈Φ, then ¬ϕ

∈Φ, ϕ

∈Φ,○

∈Φ,◆ϕ

∈Φ,□ϕ

∈Φ,◇ϕ

∈Φ,ϕ

∪ϕ

∈Φ;

∧

3 ． If ϕ∈Φ and π∈Π, where

iii

))},,(),,,({(

jjj

wAgExuwAgExu

L=Π

, then

[π]ϕ∈Φ, <π>ϕ∈Φ;

[π]ϕ means it is certain that the execution of

actions in π lead to a state in which ϕ is True; <π>ϕ

means it is possible that the execution of actions in π

lead to a state in which ϕ is True.

2.3 The Semantic of Negotiation

Logic

Definition 2.3.1 The negotiation model is defined as

M =<G

, ρ, λ>, where:

 G

⊆E×S×L

×…×L

is the set of all

possible multi-agent world states; the

element ε

of G

is (n+2)-ary tuple (e,s, l

, …, l

) called as global state;

 ρ:G

×Π→ G

, is a function that defines

the accessibility relation from states

associated with the action tuple to state.

For instance, if there is a state ε

∈G

which the execution of actions in π

produces a new state ε

∈G

, then (ε

,ε

) is

said to be “reachable”, denoted (ε

)∈ρ( π);

 λ:Φ→2

, is the interpretation function

for formulae; for ϕ∈Φ and ε

∈G

, λ(ϕ)

refers to the set of states in which ϕ holds,

and ε

∈λ(ϕ) if and only if ϕ holds in ε

Definition2.3.2 Semantic rules of negotiating logic:

<M, ε

> │＝ true

<M, ε

> │＝ ϕ iff ε

∈λ(ϕ)

<M, ε

> │＝ ¬ϕ iff <M, ε

>│≠ ϕ

<M, ε

> │＝ ϕ ∧ ψ iff <M, ε

> │＝ ϕ且<

M, ε

> │＝ ψ

<M, ε

> │＝ ○ϕ iff, <M, ε

i +1

> │＝ ϕ

<M, ε

> │＝ □ϕ iff 对∀ε

∈G

：

, <M,

> │＝ ϕ

<M, ε

> │＝ ◇ϕ, iff ∃ ε

∈G

：

, <M,

> │＝ ϕ

<M, ε

> │＝ ◆ϕ, iff ∃ ε

∈G

：

, <M,

> │＝ ϕ

Iu <M, ε

> │＝ ϕ∪ψ iff ∃ ε

∈G

：

i p

, < M,

> │＝ ψ,and

∀

, ε

Με

<M, ε

> │＝ ϕ

Theorem 2.3.1 M, ε

│＝ [π]ϕ ⇔ M, ε

│＝

¬<π>¬ϕ

Theorem 2.3.2 M, ε

│＝ <π>ϕ ⇔ M, ε

│＝

¬[π]¬ϕ

2.4 Axiomatics of L

Transmutation rule of formulas in nego-

tiation logic

T1．Substitution rule: If ϕ, ψ are formulae of

, and ├L

ϕ, then if p is a variable in ϕ,

substituting p in ϕ with ψ, the result ϕ′ satisfies ├

ϕ′;

T2．Separation rule: From ├L

ϕ→ψ and ├

ϕ, ├L

ψ holds;

T3．Certainty rule: From ├L

ϕ, ├L

[π]ϕ

holds;

T4．Temporal rule: From├L

ϕ, ├L

△

ICEIS 2005 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

364

holds，where△

={□, ◆, ○, ◇},

From├L

and├L

, ├L

∪ϕ

holds;

The strategy of selecting action

S1．If Capable(Ag

,α) and Right(Ag

,α) and

Benefit(Ag

,Exu(Ag

,α,w) )then

Select(Ag

,α,w)

S2．If Right(Ag

,α) and Capable(Ag

,α) and

¬Right(Ag

,α) and Benefit(Ag

,Exu(Ag

,α,w))

then Entitle(Ag

,Ag

,α)

S3 ． If ¬Benefit(Ag

,Exu(Ag

,α,w)) then

¬Exu(Ag

,α,w)

3 SOUNDNESS AND COMPLETE-

NESS OF NEGOTIATION LOGIC

Theorem 3.1 (Soundness of L

) Γ├L

ϕ ⇒ Γ│＝ ϕ

Theorem 3.2 (Consistency of L

)There does not

exist formula ϕ that makes Γ├L

ϕ and Γ├L

¬ϕ

hold at the same time.

Theorem 3.3 (Completeness of L

) Γ│＝ ϕ⇒ Γ├L

ϕ.

Theorem 3.4 (Logic completeness of L

)∀ϕ∈ L

there is one and only one holds between ├L

ϕ and

├L

¬ϕ.

Theorem 3.5The TN system is uncontradictory.

4 NEGOTIATION AND ARBITRA-

GE MECHANISM OF CONFICTS

RESOLVING

Definition 4.1 arbitrage strategies

Strategy 1：

If conflict(select(Ag

,α,w), select(Ag

,α,w)) then

Exu(Ag

,α,w);

Strategy 2：

If conflict(select(Ag

,α,w),select(Ag

,α,w)) and

∃w

w) and capable(Ag

,α

) and right(Ag

,α

)

then Exu(Ag

,α,w) and Exu(Ag

,α

);

≠

Strategy 3：

If conflict(select(Ag

,α,w), select(Ag

,α,w)) and

∃w

w) and capable(Ag

,α

) and

¬right(Ag

,α

)and ∃m right(Ag

,α

) then

Entitle(Ag

,Ag

,α

) and Exu(Ag

,α,w) and Exu(Ag

);

≠

Strategy 4：

If conflict(select(Ag

,α,w),select(Ag

,α,w)) and

∃w

w) and ¬capable(Ag

,α

) and

¬right(Ag

,α

) and ∃m capable(Ag

,α

) and

right(Ag

,α

) and capable(Ag

,α

) and right(Ag

,α

)

then Exu(Ag

,α,w) and Exu(Ag

,α

) and

Exu(Ag

,α

≠

5 CONCLSION

In this paper we design a negotiation model of

Multi-Agent system based on the temporal logic in

formal theory. In this model we describe the

application of the time and the ability and right of an

agent on selecting action and negotiation process in

a Multi-Agent system, the change of the right over

time, and the free action of an agent.

REFERENCE

N.R.Jennings, P.Faratin et al. Automated Negotiation:

Prospects, Methods and Challenges, Int Journal of

Group Decision and Negotiation, 2000

Sarit Kraus, Automated Negotiation and Decision Making

in Multiagent Environments, 9

ECCAI, ACAI 2001,

EASSS 2001 P151-171

Pietro Panzarasa and Nicholas R.Jennings, Formalizing

collaborative decision-making and practical reasoning

in multi-agent systems. Logic computer,

Vol.12,pp.55-117,2002

M. Wooldridge and A. Lomuscio. A Computationally

Grounded Logic of Visibility, Perception, and

Knowledge In Logic Journal of the IGPL ，

9(2):273-288, 2001.

Li Jing，Multi-Agent System based on Negotiation Axiom

System of Capability and Thought, master dissertation,

2003, Yunnan Normal University, Kunming P.R.China.

MULTI-AGENT SYSTEM FORMAL MODEL BASED ON NEGOTIATION AXIOM SYSTEM OF TEMPORAL

LOGIC

365