
Incorporating Context into Recommender Systems
Using Multidimensional Rating Estimation Methods
Gediminas Adomavicius
1
and Alexander Tuzhilin
2
1
Department of Information and Decision Sciences,
Carlson School of Management, University of Minnesota,
Minneapolis, MN 55455, USA
2
Department of Information, Operations, and Management Sciences,
Stern School of Business, New York University,
New York, NY 10012, USA
Abstract. Traditionally recommendation technologies have been focusing on
recommending items to users (or users to items) and typically do not consider
additional contextual information, such as time or location. In this paper we
discuss a multidimensional approach to recommender systems that supports ad-
ditional dimensions capturing the context in which recommendations are made.
One of the most important questions in recommender systems research is how
to estimate unknown ratings, and in the paper we address this issue for the mul-
tidimensional recommendation space. We present the classification of multi-
dimensional rating estimation methods, discuss how to extend traditional two-
dimensional recommendation approaches to the multidimensional space, and
identify research directions for the multidimensional rating estimation problem.
Keywords. Context-aware recommender systems, collaborative filtering, rating
estimation techniques.
1 Introduction and Motivation
Recommender systems became an important and popular research area in the mid-
1990’s, when researchers started focusing on recommendation problems that explic-
itly rely on the notion of ratings [11,14]. Subsequently there has been a significant
amount of research done on developing different recommendation techniques over the
past decade [1,2,3,4,5,6,7,9,12,13,15]. These technologies are based on a broad range
of different approaches and feature a variety of methods from such disciplines as
statistics, data mining, machine learning and information retrieval. In its most com-
mon formulation, the recommendation problem is reduced to the problem of estimat-
ing ratings for the items that have not been seen by a user. This estimation is usually
based on the ratings given by the user to other items, ratings given to the item by
other users, and possibly on some other user and item information as well (e.g., user
demographics, item characteristics). Naturally, once the ratings are estimated for the
yet unrated items, the recommendations can be made to each user by presenting the
Adomavicius G. and Tuzhilin A. (2005).
Incorporating Context into Recommender Systems Using Multidimensional Rating Estimation Methods.
In Proceedings of the 1st International Workshop on Web Personalisation, Recommender Systems and Intelligent User Interfaces, pages 3-13
DOI: 10.5220/0001421700030013
Copyright
c
SciTePress

item(s) with the highest estimated rating(s).
Note that, while a substantial amount of research has been performed in the area of
recommender systems, the vast majority of the existing approaches focus on recom-
mending items to users or users to items based on the ratings information and do not
take into the consideration any additional contextual information, such as time, place,
the company of other people (e.g., for watching movies). In other words, traditionally
recommender systems have dealt with applications that have two types of entities,
users and items. In such cases, the recommendation process starts with the specifica-
tion of the initial set of ratings that is either explicitly provided by the users or is
implicitly inferred by the system. For example, in case of a movie recommender
system, John Doe may assign a rating of 7 (out of 10) for the movie “Gladiator,” i.e.,
set R
movie
(John_Doe, Gladiator)=7. Once these initial ratings are specified, a recom-
mender system tries to estimate the rating function R
R: User × Item → Rating
(1)
for the (user, item) pairs that have not been rated yet by the users. Here Rating is a
totally ordered set (e.g., non-negative integers or real numbers within a certain range).
Once function R is estimated for the whole User×Item domain, a recommender sys-
tem can recommend the highest-rated item (or k highest-rated items) for each user.
While the current generation of recommendation technologies performs well in
several applications, including the ones for recommending books, CDs, and news
articles [10,13], the traditional two-dimensional (2D) framework described in Equa-
tion (1) is restrictive and is not sufficient to capture the intricacies of more complex
applications, such as recommending vacations or financial services, and needs to be
extended in order to overcome its inherent limitations. For this purpose, in the prior
research a multidimensional (MD) approach to recommendations has been proposed,
where the traditional recommendation framework (1) is extended to support addi-
tional dimensions capturing the context in which recommendations are made [1].
This multidimensional approach explores the synergies between recommender sys-
tems and the multidimensional data model used for data warehousing and On-Line
Analytical Processing (OLAP) applications in databases [8] and provides recommen-
dations not only over the two traditional dimensions (i.e., User and Item), as the clas-
sical (2D) recommender systems do, but over several additional dimensions, such as
Time, Place, etc.
More formally, given dimensions D
1
, D
2
, …, D
n
, the recommendation space for
these dimensions is defined as a Cartesian product S = D
1
× D
2
× …× D
n
. Moreover,
let Rating be a rating domain representing the ordered set of all possible rating values.
In order to take into consideration the contextual information (e.g., the date, time, and
the companion in movie recommendations), the utility function (or rating function) R
over a multidimensional space D
1
× D
2
× …× D
n
(as opposed to the traditional 2-
dimensional User×Item space) is defined as:
R: D
1
× D
2
× …× D
n
→ Rating
(2)
An important research question is how to estimate unknown ratings in a multidi-
mensional recommendation space. As in traditional recommender systems, the key
problem in multidimensional systems is the extrapolation of the rating function from
4

a (usually small) subset of ratings that are specified by the users. Since there has been
much work done on estimating these ratings for the 2D case, it would be advanta-
geous to leverage this work. One natural approach would be to reduce the multidi-
mensional rating estimation problem to the 2D case. This approach was proposed in
[1], where it was call the reduction-based approach. Alternatively to the reduction-
based approach, it may be possible to extend some existing 2D methods to the multi-
dimensional case. Since the 2D methods are often broadly classified into heuristic-
and model-based approaches [6], we follow this classification when considering the
extension of 2D methods to the MD recommendation space. Therefore, combining
the reduction- and the extension-based approaches, we can classify multidimensional
rating estimation methods into: (a) reduction-based, (b) heuristic-based, and (c)
model-based.
In the rest of this paper we discuss the above three classes of multidimensional rat-
ing estimation (in Sections 2, 3, and 4, respectively), provide examples of possible
estimation methods, and outline several directions for future research. The contribu-
tions and the conclusions of the paper are presented Section 5.
2 Reduction-Based Approach
The reduction-based approach [1] is arguably the most straightforward way to apply
traditional two-dimensional rating estimation methods for multidimensional recom-
mendations. Using this approach, the problem of multidimensional recommendations
is reduced to the traditional two-dimensional User×Item recommendation space, and,
therefore, any available 2D rating estimation method can be applied directly in this
case. The reduction can be done in several ways. Consider the multidimensional
recommender system with three dimensions User, Item, and Time, and assume that
R
D
: User×Item → Rating is a two-dimensional rating estimation function that, given
existing ratings D (i.e., D contains records <user, item, rating> for each of the user-
specified ratings), can calculate a prediction for any rating, e.g., R
D
(“John”, “Dow-
JonesReport”) = 5. A 3-dimensional rating prediction function supporting time can
be defined similarly as R
D
: User×Item×Time → Rating, where D contains records
<user, item, time, rating> for the user-specified ratings. Then the 3-dimensional
prediction function can be expressed through a 2-dimensional prediction function as
follows:
∀(u,i,t)∈ User×Item×Time, R
D
(u,i,t) = R
D[Time=t] (User, Item, Rating)
(u,i)
(3)
where D[Time=t](User,Item,Rating) denotes a rating set obtained from D by selecting
only the records where Time dimension has value t and keeping only the values for
User and Item dimensions as well as the value of the rating itself. In other words, if
we treat a set of 3-dimensional ratings D as a relation, then D[Time=t](User,Item,
Rating) is simply another relation obtained from D by performing two relational op-
erations: selection and, subsequently, projection. “Time = t” is called a contextual
segment for this recommendation application.
For example, in order to predict how John would like the Dow Jones Report in the
morning, i.e., in order to calculate R
D
(“John”, “DowJonesReport”, “Morning”), the
5

reduction-based approach would proceed as follows. First, it would eliminate the
Time dimension by selecting only the morning ratings from the set of all ratings D.
As a result, the problem is reduced to the standard User×Item case on the set of morn-
ing ratings. Then, using any traditional 2D rating estimation technique [2], we can
calculate how John likes the Dow Jones Report based on the set of these morning
ratings. In other words, this approach would use the two-dimensional function
R
D[Time=t] (User, Item, Rating)
to estimate ratings for the User×Item domain. The intuition
behind this approach is simple: if we want to predict a “morning” rating for a certain
user and a certain content item, we should consider only the previously specified
“morning” ratings for the rating estimation purposes.
Note, that in this example we chose to eliminate the Time dimension and left the
traditional User and Item dimensions for the two-dimensional estimation of ratings.
However, one could choose to eliminate other dimensions instead of Time, e.g., User
or Item. Which dimension(s) should be eliminated in the reduction-based approach
constitutes an interesting problem for future research. Furthermore, the reduction-
based algorithm [1] uses the same two-dimensional recommendation method (e.g.,
traditional memory-based collaborative filtering [6]) for all discovered contextual
segments. This approach can be extended to incorporate several two-dimensional
recommendation methods, since potentially different recommendation algorithms can
perform the best on different contextual segments. Finally, another way to improve
the reduction-based approach is by “extending” the notion of contextual segments to
include not only the segments of contextual dimensions, such as Time and Place, but
also the segments defined by “slicing” the main dimensions, such as User and Item.
For example, segment Frequent-Moviegoers, consisting of the users who usually
watch a lot of movies, may be very interesting from the marketing perspective and
should deserve a special treatment. While it is not strictly a contextual segment since
it is defined in terms of the user characteristics and not in terms of the contextual
dimensions Time, Place, and Companion, the definition of contextual segments can
be straightforwardly extended to include such segments.
The main benefit of the reduction-based approach is that all the previous research
on two-dimensional recommender systems is directly applicable in the multidimen-
sional case. On the other hand, only a part of data (i.e., two-dimensional “slices” of
the multidimensional space) is actively involved in the rating prediction process.
3 Heuristic-Based Approaches
As mentioned before, the reduction-based approach is not the only one for estimating
multidimensional ratings. In fact, several traditional two-dimensional recommenda-
tion methods could be directly extended to the multidimensional case.
A large number of commonly used recommender systems techniques are two-
dimensional heuristic-based collaborative filtering methods [6,9,11,12,14] and some
of them may be extended to multiple dimensions. More specifically, in many tradi-
tional collaborative filtering methods the prediction of rating r
u,i
(i.e., the rating how
user u would like item i) is computed as a weighted sum of the ratings given to the
same item i by similar users u':
6
,,
(, )
ui u i
u Users
rk simuur
′
′
∈
′
=×
∑
(4)
where k is a normalizing factor. In other words, it constitutes a “nearest neighbors”
problem, where we need to discover the “closest” neighbors among those who rated a
given item.
Furthermore, if we look at the traditional two-dimensional content-based recom-
mender systems [4,10], some of the heuristic algorithms used in such systems also
employ the nearest neighbor approach, although in a different manner. In particular,
the prediction of rating r
u,i
is computed as an aggregation (e.g., a weighted sum) of
the ratings given by the same user u to similar items i'. Therefore, the prediction of a
particular rating r
u,i
in many heuristic-based approaches in two-dimensional recom-
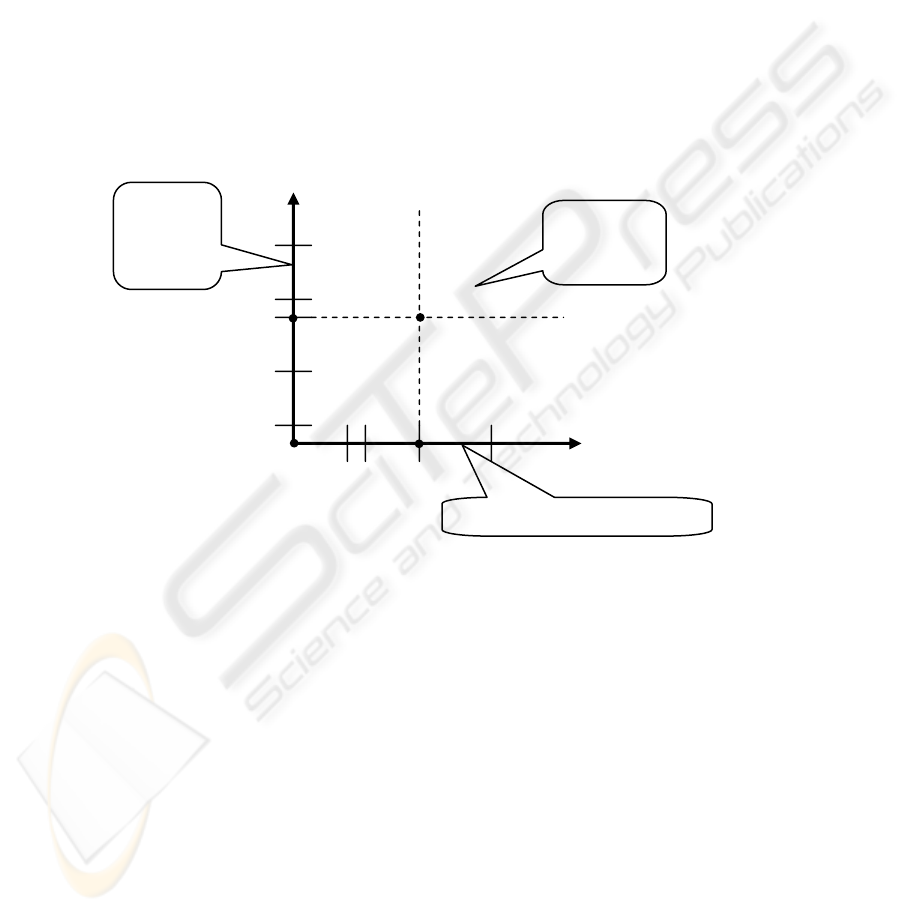
mender systems (both collaborative and content-based) can be represented by Fig. 1,
which can be interpreted as follows.
Fig. 1. Data used by nearest neighbor-based approaches in the traditional two-dimensional
heuristic-based recommender systems
Let’s assume that we want to predict rating r
u,i
, which is depicted as the origin
point in the figure. The horizontal axis represents all the users u' arranged according
to their similarity to user u using some distance measure, and the vertical axis depicts
all the items i' according to their similarity to item i. All the known data (i.e., all
user/item pairs with a known rating) can be described as points in the resulting two-
dimensional space. Furthermore, as mentioned earlier, many two-dimensional heuris-
tic-based collaborative filtering systems would use the ratings on the horizontal axis
(i.e., how users that are similar to u rated item i) to predict rating r
u,i
. Similarly, the
content-based systems usually use the ratings on the vertical axis (i.e., how items that
are similar to item i were rated by user u) to predict rating r
u,i
. The hybrid heuristic-
based approaches typically combine the collaborative and content-based ideas [2,4,7].
However, virtually all of them use some combination of the information represented
(u',i')
(u',i)
Users,
according to their
similarity to u
(u,i')
(u,i)
Items, according to their similarity to i
Used by
content-
based
systems
Used by collaborative systems
Generally
not used for
prediction
7

by the two axes. Therefore, user-specified ratings r
u',i'
(where u' ≠ u and i' ≠ i) lying
outside of the two axes are usually not used for the prediction of r
u,i
(e.g., in the
weighted sum (4)) in the traditional heuristic-based recommendation approaches.
1
Based on this discussion, we can generalize this two-dimensional heuristic ap-
proach to multiple dimensions as follows. First, we can generalize this approach by
introducing a two-dimensional distance metric between two arbitrary rating points
(u,i) and (u',i') in the entire User×Item space. By using the entire two-dimensional
space in the prediction process instead of just the data on the two axes (as shown in
Fig. 1) we will be able to (a) incorporate collaborative and content-based approaches
as special cases and (b) identify additional nearest neighbors that lie outside of the
User and Item axes and that were not even considered by collaborative and content-
based approaches. Arguably, by identifying extra nearest neighbors that were not
considered before, we should increase the predictive accuracy of recommendations.
The choice of a specific distance metric (Euclidian, etc.) depends largely on a specific
application domain. For example, one metric may work better for recommending
movies and another metric for news articles. Identification of appropriate metrics for
different applications constitutes an interesting problem for future research.
Second, we can extend the two-dimensional nearest neighbor approach described
above to multidimensional recommendation spaces (i.e., that include contextual in-
formation) in a straightforward manner by using an n-dimensional distance metric
instead of a two-dimensional metric mentioned above. To see how this is done, con-
sider an example of the User×Item×Time recommendation space. Following the
traditional nearest neighbor heuristic that is based on the weighted sum, the prediction
of a specific rating r
u,i,t
in this example can be expressed as:
(
)
(
)
(
)
()
,, ,,
,, (,,)
,, , , ,
uit u i t
uit uit
rk Wuituitr
′
′′
′′′
≠
′′′
=×
∑
(5)
where W((u,i,t),(u',i',t')) describes the “weight” rating r
u',i',t'
carries in the prediction of
r
u,i,t
, and k is a normalizing factor. Weight W((u,i,t),(u',i',t')) is typically inversely
related to the distance between points (u,i,t) and (u',i',t') in multidimensional space,
i.e., dist[(u,i,t),(u',i',t')]. In other words, the closer the two points are (i.e., the smaller
the distance between them), the more weight r
u',i',t'
carries in the weighted sum (5).
One example of such relationship would be W((u,i,t),(u',i',t')) = 1 /
dist[(u,i,t),(u',i',t')], but many alternative specifications are also possible. As before,
the choice of the specific distance metric dist is likely to depend on a specific applica-
tion. This idea is depicted in Fig. 2, where we have a three-dimensional recom-
mender system with User, Item, and Time dimensions, and where ratings, equidistant
from the rating to be predicted are schematically represented with concentric spheres.
The distance function dist can be defined in various ways. One of the simplest
ways to define a multidimensional dist function is by using the reduction-like ap-
proach (similar to the one described in Section 2), by taking into account only the
points with the same contextual information, i.e.,
1
In collaborative filtering systems, r
u',i'
may be used for computing the similarity between two
users, but it is usually absent in the weighted sum that represents the predicted rating.
8
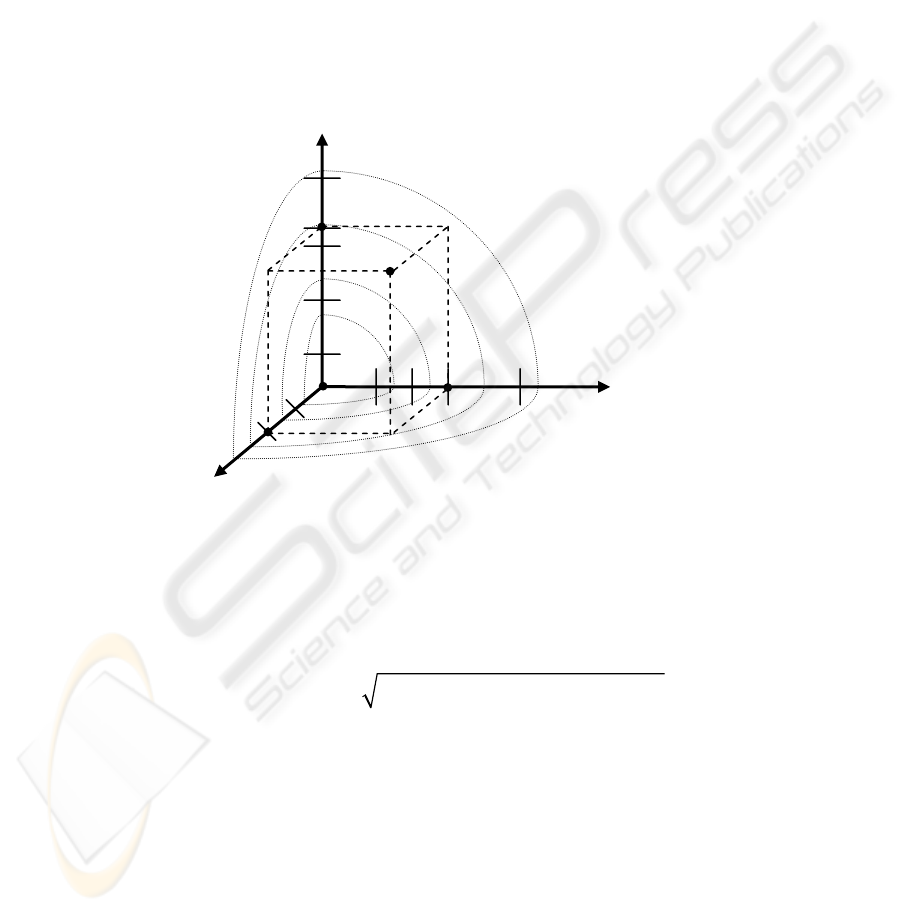
[]
[
]
, if '
+ , otherwise
(,),( ,)
(,,),( ,,')
dist t t
dist
ui u i
uit u i t
=
=
∞
′′
′′
⎧
⎨
⎩
(6)
This distance function makes r
u,i,t
depend only on the ratings from the segment of
points having the same values of time t. Therefore, this case is reduced to the stan-
dard 2-dimensional rating estimation on the segment of ratings having the same con-
text t as point (u,i,t). Furthermore, if we further refine function dist[(u,i),(u',i')] in (6)
so that it depends only on the distance between users when i = i', then we would ob-
tain a method that is similar to the reduction-based approach described in Section 2.
Moreover this approach easily extends to an arbitrary n-dimensional case by setting
the distance d between 2 rating points to dist[(u,i),(u',i')] if and only if the contexts of
these two points are the same.
Fig. 2. Data used by nearest neighbor-based approaches in the multidimensional heuristic-
based recommender systems
Other ways to define the distance function would be to use the weighted Manhat-
tan distance metric, i.e.,
[
]
11 2 2 3 3
(,,),( , , ) (, ) (, ) (, )dist uit u i t wd uu wd ii wd tt
′′′ ′′′
=++,
or the weighted Euclidean distance metric, i.e.,
[]
222
11 2 2 3 3
(,,),( , , ) (, ) (, ) (, )dist uit u i t wd uu wd ii wd tt
′′′ ′ ′ ′
=++,
where d
1
, d
2
, and d
3
are distance functions defined for dimensions User, Item, and
Time respectively, and w
1
, w
2
, and w
3
are the weights assigned for each of these di-
mensions. In summary, distance function dist[(u,i,t),(u',i',t')] can be defined in many
different ways, and it constitutes an interesting research problem to identify various
ways to define this distance and compare these different ways in terms of predictive
performance.
Items
(u',i',t')
(u',i,t)
(u,i',t)
(u,i,t')
(u,i,t)
Time
Users
9

4 Model-Based Approaches
There have been several model-based recommendation techniques proposed in re-
commender systems literature for the traditional two-dimensional recommendation
model [3,5,6,15]. Some of these methods can be directly extended to the multidimen-
sional case, such as the method proposed in [3], who show that their 2D technique
outperforms some of the previously known collaborative filtering methods.
The method proposed by [3] combines the information about users and items into a
single hierarchical regression-based Bayesian preference model that uses Markov
Chain Monte Carlo (MCMC) techniques for exact estimation and prediction. In par-
ticular, this Bayesian preference model allows statistical integration of the following
types of information useful for making recommendations of items to users: a person's
expressed preferences (ratings), preferences of other consumers, expert evaluations,
item characteristics, and characteristics of individuals. For example, for recommend-
ing movies this information may include known movie ratings, gender and age of
users, movie genres, and movie reviews by critics. Formally, [3] propose a linear
model of rating estimation:
2
, (0, ), (0, ), (0, )
ui ui u i i u ui ui u i
rx z w eeN N N
µγ λ σλ γ
′′ ′
=+++ ∼ ∼ Λ ∼ Γ
(7)
where r
ui
represents the rating of user u (movie-goer) for item i (which will be used
interchangeably with “movie”). The vector x
ui
represents all the observed parameters
for user u, item i, and their interactions. Observed parameters would be the parame-
ters explicitly recorded in the profiles of the users, such as gender, age, and movie
preferences, and in the profiles of items, such as genre, year and expert ratings of a
movie. Interaction terms represent second-order interaction effects between observed
user and item attributes. For example, there can be an interaction term in x
ui
repre-
senting second-order effects between gender and genre (e.g., even though overall
romantic movies appear to get higher ratings than action movies, men might rate
action movies higher than romantic movies). The coefficient of x
ui
is
µ
which repre-
sents the fixed effects in the regression. The term z
u
contains the observed attributes
of user u, such as gender, age, and movie preferences, and w
i
represents the observed
attributes of item i such as genre, year and expert ratings. The unobserved effects of
the movies, that are not explicitly recorded in the movie profiles, such as direction,
music, acting, etc., are captured by the vector of random variables
γ
i
that is normally
distributed as
γ
i
~ N(0,Γ). Unobserved user-effects are represented by
λ
u
~ N(0,Λ).
The error term e
ui
belongs to a normal distribution with mean zero and standard devia-
tion
σ
. x'
ui
, z'
u
and w'
i
denote the transposes of the corresponding vectors. The pa-
rameters
µ
,
σ
2
, Λ and Γ of model (7) are estimated from the data of already known
ratings using MCMC methods.
While the approach presented in [3] is described in the context of traditional two-
dimensional recommender systems, it can be directly extended to combine more di-
mensions (i.e., the contextual information) in addition to users and items. For exam-
ple, assume that we have a third dimension Time that is defined by the following two
attributes (variables): (a) Boolean variable weekend specifying whether a movie was
10

seen on a weekend or not, and (b) a positive integer variable numdays indicating the
number of days after the release when the movie was seen.
In such a case, the [3] model can be extended to the third (Time) dimension as
r
uit
= x'
uit
µ
+ p'
ui
θ
t
+ q'
it
λ
u
+ r'
tu
γ
i
+ z'
u
δ
it
+ w'
i
π
tu
+ y'
t
σ
ui
+ e
uit
(8)
where e
uit
~ N(0,
σ
2
),
γ
i
~ N(0,Γ),
λ
u
~ N(0,Λ),
θ
t
~ N(0,Θ),
δ
it
~ N(0,∆),
π
tu
~ N(0,Π),
and
σ
ui
~N(0,Σ).
This model encompasses the effects of observed and unobserved user-, item- and
temporal-variables and their interactions on rating r
uit
of user u for movie i seen at
time t. The variables z
u
, w
i
and y
t
stand for the observed attributes of users (e.g.
demographics), movies (e.g. genre) and time dimension (e.g. weekend, numdays).
The vector x
uit
represents the observed parameters of users, movies and time, and their
interaction effects, and its coefficient
µ
represents the fixed effects in the regression.
The vectors
λ
u
,
γ
i
and
θ
t
are random effects that stand for the unobserved sources of
heterogeneity of users (e.g. their ethnic background), movies (e.g. the story, screen-
play, etc.) and temporal effects (e.g. was the movies seen on a holiday or not, the
season when it was released, etc). The vector p
ui
represents the interaction of the
observed user and item variables, and likewise q
it
and r
tu
. The vector
σ
ui
represents
the interaction of the unobserved user and item attributes, and likewise
π
tu
and
δ
it
.
Finally, the parameters
µ
,
σ
2
, Λ, Γ, Θ, ∆, Π and Σ of the model can be estimated from
the data of already known ratings using Markov Chain Monte Carlo (MCMC) meth-
ods as was done in (7). [3] assume that the features (attributes) in vectors z
u
, w
i
and y
t
are already specified. In more general cases, these features need to be selected, and
various machine learning methods can be used for this purpose.
Finally, note that the number of parameters in the above model that would need to
be estimated rises with the number of dimensions and, therefore, the sparsity of
known ratings may become a problem. Therefore, one of the research challenges is to
make such models scalable for the sparse contexts with a large number of dimensions.
5 Conclusions
Traditionally, the vast majority of recommender systems technologies has been focus-
ing on recommending items to users or users to items and typically do not take into
the consideration any additional contextual information, such as time or place. In this
paper we discuss a multidimensional approach to recommendations which supports
additional dimensions capturing the context in which recommendations are made.
One of the most important questions in recommender systems research is how to
estimate unknown ratings, and in the paper we address this issue for a multidimen-
sional recommendation space.
The contributions of this paper include: (a) the classification of multidimensional
rating estimation methods into reduction-, heuristic-, and model-based approaches,
(b) the discussion on how to extend the traditional two-dimensional heuristic- and
model-based recommendation approaches to the multidimensional recommendation
space, and (c) the identification of various research directions for the multidimen-
sional rating estimation problem.
11

We believe that our classification of multidimensional rating estimation methods
represents the natural evolution of research in this area. The area of multidimensional
recommender systems is very young and there have been no real-life implementations
of multidimensional heuristic- or model-based methods. Therefore, the obvious
choice at this point is to reduce the multidimensional rating estimation problem to the
standard two-dimensional one, for which there is a large number of estimation algo-
rithms available. Not surprisingly, the only implementation of multidimensional
recommender systems has been reduction-based [1], which already demonstrated
performance improvements over the traditional two-dimensional recommender sys-
tems. Eventually, multidimensional heuristic-based rating estimation methods will be
developed and implemented, and they are expected to outperform reduction-based
approaches, since they will be able to take into account the contextual dimensions
directly (unlike the reduction-based approaches operating with 2D slices of the rec-
ommendation space). Finally, since the model-based rating estimation methods typi-
cally outperform heuristic-based approaches in the traditional 2D recommendation
space [6], we expect that the same would happen in the MD case, i.e., the model-
based approaches would eventually outperform the heuristics, especially when they
address the sparsity and scalability issues, as mentioned in Section 4.
In summary, we believe that context-aware recommender systems constitute an
important and problem-rich research area and that the multidimensional rating estima-
tion methods will play a significant role in their development.
References
1. Adomavicius, G., R. Sankaranarayanan, S. Sen, A. Tuzhilin. Incorporating Contextual
Information in Recommender Systems Using a Multidimensional Approach. ACM Transac-
tions on Information Systems, 23(1):103-145, 2005.
2. Adomavicius, G., A. Tuzhilin. Towards the next generation of recommender systems: a
survey of the state-of-the-art and possible extensions. IEEE Transactions on Knowledge and
Data Engineering, 17(6):734-749, 2005.
3. Ansari, A., S. Essegaier, R. Kohli. Internet recommendations systems. Journal of Market-
ing Research, pages 363-375, August 2000.
4. Balabanovic, M., Y. Shoham. Fab: Content-based, collaborative recommendation. Commu-
nications of the ACM, 40(3):66-72, 1997.
5. Basu, C., H. Hirsh, W. Cohen. Recommendation as Classification: Using Social and Con-
tent-Based Information in Recommendation. Proc. of the 15
th
National Conf. on AI, 1998.
6. Breese, J. S., D. Heckerman, C. Kadie. Empirical analysis of predictive algorithms for
collaborative filtering. Proceedings of the 14
th
Conf. on Uncertainty in AI, 1998.
7. Burke, R. Hybrid Recommender Systems: Survey and Experiments. User Modeling and
User-Adapted Interaction, 12(4):331-370, 2002.
8. Chaudury, S., U. Dayal. An overview of data warehousing and OLAP technology. ACM
SIGMOD Record, 26(1):65-74, 1997.
9. Delgado, J., N. Ishii. Memory-based weighted-majority prediction for recommender sys-
tems. In ACM SIGIR’99 Workshop on Recommender Systems: Algorithms and Evaluation.
10. Mooney, R. J., L. Roy. Content-based book recommending using learning for text catego-
rization. Proceedings of the 5
th
ACM Conference on Digital Libraries, pp. 195-204, 2000.
12

11. Resnick, P., N. Iakovou, M. Sushak, P. Bergstrom, J. Riedl. GroupLens: An open architec-
ture for collaborative filtering of netnews. Proceedings of CSCW’94 Conference, 1994.
12. Sarwar, B., G. Karypis, J. Konstan, J. Riedl. Item-based Collaborative Filtering Recom-
mendation Algorithms. Proceedings of the 10
th
International WWW Conference, 2001.
13. Schafer, J. B., J. A. Konstan, J. Riedl. E-commerce recommendation applications. Data
Mining and Knowledge Discovery, 5(1/2):115-153, 2001.
14. Shardanand, U., P. Maes. Social information filtering: Algorithms for automating ‘word of
mouth’. Proceedings of CHI’95 Conference, 1995.
15. Soboroff, I., C. Nicholas. Combining content and collaboration in text filtering. In
IJCAI'99 Workshop: Machine Learning for Information Filtering, 1999.
13
