Data Quality and Sparsity Issues in Collaborative

Filtering on Web Logs

Miha Gr

car, Dunja Mladeni

c and Marko Grobelnik

J. Stefan Institute, Jamova 39, 1000 Ljubljana, Slovenia

Abstract. In this paper, we present our experience in applying collaborative ﬁl-

tering to real-life corporate data in the light of data quality and sparsity. The qual-

ity of collaborative ﬁltering recommendations is highly dependent on the quality

of the data used to identify users’ preferences. To understand the inﬂuence that

highly sparse server-side collected data has on the accuracy of collaborative ﬁlter-

ing, we ran a series of experiments in which we used publicly available datasets

and, on the other hand, a real-life corporate dataset that does not ﬁt the proﬁle of

ideal data for collaborative ﬁltering. We have also experimentally compared two

standard distance measures (Pearson correlation and Cosine similarity) used by

k-Nearest Neighbor classiﬁer, showing that depending on the dataset one outper-

forms the other - but no consistent difference can be claimed.

1 Introduction

Data quality is recognized as an important issue for different problems where the re-

sults highly rely on the data, such as machine learning, data mining or recommendation

systems. In addition, a problem of data sparsity is recognized as important in recom-

mendation systems especially when based on collaborative ﬁltering. The goal of collab-

orative ﬁltering in general is to explore a vast collection of items in order to detect those

which might be of interest to the active user. In contrast to content-based recommender

systems which focus on ﬁnding contents that best match the user’s query, collaborative

ﬁltering is based on the assumption that similar users have similar preferences. It ex-

plores the database of users’ preferences and searches for users that are similar to the

active user. The active user’s preferences are then inferred from preferences of the simi-

lar users. One of the main advantages of pure collaborative ﬁltering is that it ignores the

form and the content of items and can therefore also be applied to non-textual items.

The accuracy of collaborative ﬁltering recommendations is highly dependent on the

quality of the users’ preferences database. In this paper we would like to emphasize the

differences between applying collaborative ﬁltering to publicly available datasets and,

on the other hand, to a dataset derived from real-life corporate Web logs. The latter does

not ﬁt the proﬁle of ideal data for collaborative ﬁltering.

The rest of this paper is arranged as follows. In Sections 2 and 3 we discuss collab-

orative ﬁltering algorithms and data quality for collaborative ﬁltering. Our evaluation

platform and the three datasets used in our experiments are described in Sections 4 and

5. In Sections 6 and 7 the experimental setting and the evaluation results are presented.

The paper concludes with the discussion and some ideas for future work (Section 8).

Grc

ar M., Mladeni

c D. and Grobelnik M. (2005).

Data Quality and Sparsity Issues in Collaborative Filtering on Web Logs.

In Proceedings of the 1st International Workshop on Web Personalisation, Recommender Systems and Intelligent User Interfaces, pages 89-97

DOI: 10.5220/0001421500890097

 SciTePress

2 Collaborative ﬁltering

There are basically two approaches to the implementation of a collaborative ﬁlter-

ing algorithm. The ﬁrst one is the so called “lazy learning” approach (also known as

the memory-based approach) which skips the learning phase. Each time it is about to

make a recommendation, it simply explores the database of user-item interactions. The

model-based approach, on the other hand, ﬁrst builds a model out of the user-item in-

teraction database and then uses this model to make recommendations. “Making rec-

ommendations” is equivalent to predicting the user’s preferences for unobserved items.

The data in the user-item interaction database can be collected either explicitly (ex-

plicit ratings) or implicitly (implicit preferences). In the ﬁrst case the user’s participation

is required. The user is asked to explicitly submit his/her rating for the given item. In

contrast to this, implicit preferences are inferred from the user’s actions in the context

of an item (that is why the term “user-item interaction” is used instead of the word

“rating” when referring to users’ preferences in this paper). Data can be collected im-

plicitly either on the client side or on the server side. In the ﬁrst case the user is bound

to use modiﬁed client-side software that logs his/her actions. Since we do not want to

enforce modiﬁed client-side software, this possibility is usually omitted. In the second

case the logging is done by a server. In the context of the Web, implicit preferences can

be determined from access logs that are automatically maintained by Web servers.

Collected data is ﬁrst preprocessed and arranged into a user-item matrix. Rows rep-

resent users and columns represent items. Each matrix element is in general a set of

actions that a speciﬁc user took in the context of a speciﬁc item. In most cases a matrix

element is a single number representing either an explicit rating or a rating that was

inferred from the user’s actions.

Since a user usually does not access every item in the repository, the vector (i.e. the

matrix row), representing the user, is missing some/many values. To emphasize this, we

use the terms “sparse vector” and “sparse matrix”.

The most intuitive and widely used algorithm for collaborative ﬁltering is the so

called k-Nearest Neighbors algorithm which is a memory-based approach. Technical

details can be found, for example, in [6]. The algorithm is as follows:

1. Represent each user by a sparse vector of his/her ratings.

2. Deﬁne the similarity measure between two sparse vectors. In this paper, we con-

sider two widely used measures: (i) the Pearson correlation coefﬁcient which is

used in statistics to measure the degree of correlation between two variables [12],

and (ii) the Cosine similarity measure which is originally used in information re-

trieval to compare between two documents (introduced by Salton and McGill in

1983).

3. Find k users that have rated the item in question and are most similar to the active

user (i.e. the user’s neighborhood).

4. Predict the active user’s rating for the item in question by calculating the weighted

average of the ratings given to that item by other users from the neighborhood.

3 Sparsity problem and data quality for collaborative ﬁltering

The fact that we are dealing with a sparse matrix can result in the most concerning

problem of collaborative ﬁltering – the so called sparsity problem. In order to be able

to compare two sparse vectors, similarity measures require some values to overlap.

Furthermore, the lower the amount of overlapping values, the lower the relialibility of

these measures. If we are dealing with high level of sparsity, we are unable to form

reliable neighborhoods. Furthermore, in highly sparse data there might be many un-

rated (unseen) items and many inactive users. Those items/users, unfortunately, cannot

participate in the collaborative ﬁltering.

Sparsity is not the only reason for the inaccuracy of recommendations provided

by collaborative ﬁltering. If we are dealing with implicit preferences, the ratings are

usually inferred from the user-item interactions, as already mentioned earlier in the

text. Mapping implicit preferences into explicit ratings is a non-trivial task and can

result in false mappings. The latter is even more true for server-side collected data in

the context of the Web since Web logs contain very limited information. To determine

how much time a user was reading a document, we need to compute the difference in

time-stamps of two consecutive requests from that user. This, however, does not tell us

weather the user was actually reading the document or he/she, for example, went out

to lunch, leaving the browser opened. Furthermore, the user may be accessing cached

information (either from a local cache or from an intermediate proxy server cache) and

there is no way to detect these events on the server side.

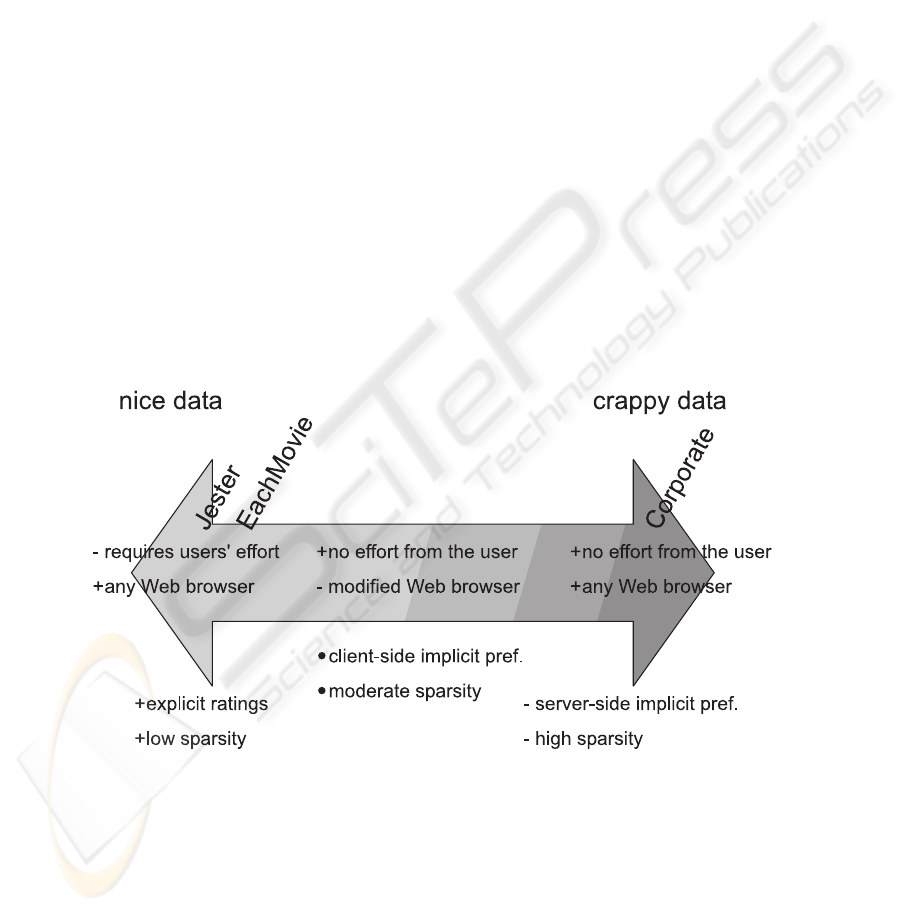
Fig.1. Data characteristics that inﬂuence the data quality, and the positioning of the three datasets

used in our experiments, according to their properties.

Also, if a user is not logged in and he/she does not accept cookies, we are unable to

track him/her. In such case, the only available information that could potentially help us

to track the user is his/her IP address. However, many users can share the same IP and,

furthermore, one user can have many IP addresses even in the same session. The only

reliable tracking mechanisms are cookies and requiring users to log in order to access

relevant contents.

From this brief description of data problems we can conclude that for applying

collaborative ﬁltering, explicitly given data with low sparsity are preferred to implicitly

collected data with high sparsity (as also pointed out in [7]). The worst case scenario

is having highly sparse data derived from Web logs. So why would we want to apply

collaborative ﬁltering to Web logs? The answer is that collecting data in such manner

requires no effort from the users and also, the users are not obliged to use any kind of

specialized Web browsing software. This “conﬂict of interests” is illustrated in Figure 1.

4 Evaluation platform

To understand the inﬂuence that highly sparse server-side collected data has on the ac-

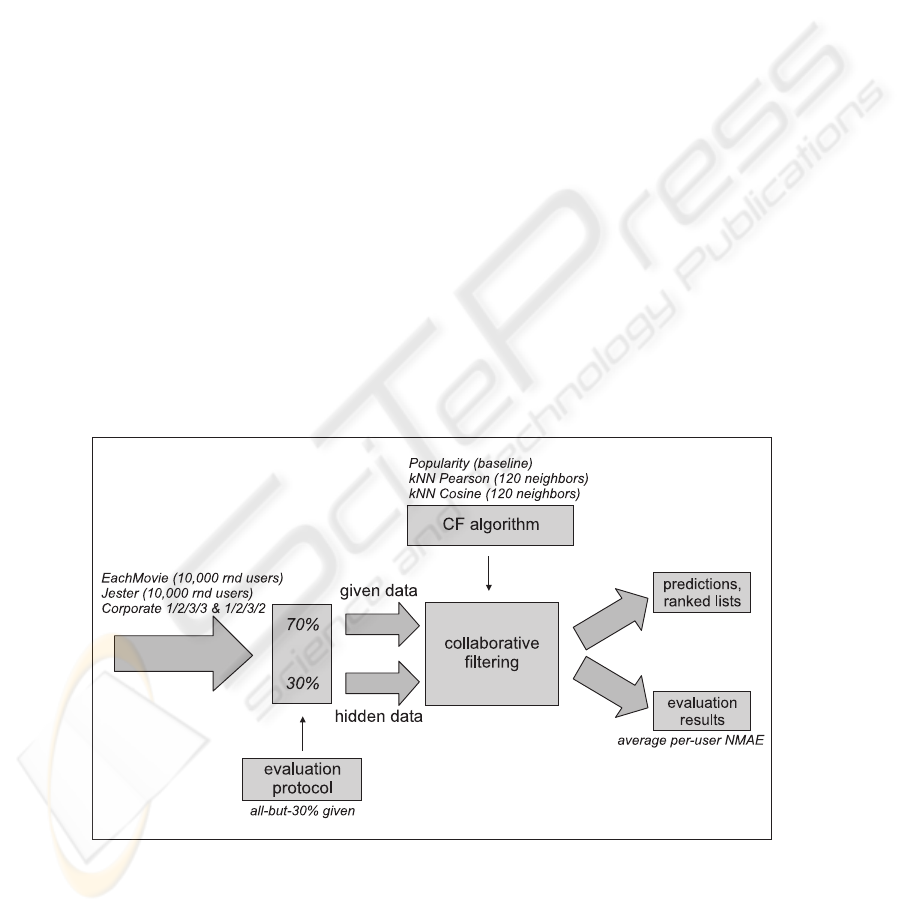
curacy of collaborative ﬁltering, we built an evaluation platform. This platform is a set

of modules arranged into a pipeline. The pipeline consists of the following four con-

secutive steps: (i) importing a user-item matrix (in the case of implicit preferences, data

needs to be preprocessed prior to entering the pipeline), (ii) splitting data according to

an evaluation protocol, (iii) setting a collaborative ﬁltering algorithm (in the case of

the kNN algorithm we also need to specify a similarity measure), (iv) making predic-

tions about users’ ratings and collecting evaluation results. The platform is illustrated

in Figure 2.

Fig.2. The evaluation platform. The notes in italics illustrate our experimental setting (see Sec-

tion 6).

Let us brieﬂy discuss some of these stages. In the process of splitting the data,

ratings from each user are partitioned into “given” and “hidden” ratings, according

to the evaluation protocol. Notice that this is different from splitting all the users to

training and testing as used in [7]. For example, 30% of randomly selected ratings from

a particular user are hidden, the rest are treated as our sole knowledge about the user (i.e.

given ratings). Given ratings are used to ﬁnd neighbors, while hidden ratings are used

to evaluate the accuracy of the selected collaborative ﬁltering algorithm. The algorithm

predicts the hidden ratings and since we know their actual values, we can compute the

mean absolute error (MAE) or apply some other evaluation metric.

5 Data description

For our experiments we used three distinct datasets. The ﬁrst dataset was EachMovie

(provided by Digital Equipment Corporation) which contains explicit ratings for movies.

The service was available for 18 months. The second dataset with explicit ratings was

Jester (provided by [5]) which contains ratings for jokes, collected over a 4-year pe-

riod. Users were using a scrollbar to express their ratings – they had no notion of actual

values. The third dataset was derived from real-life corporate Web logs. The logs con-

tain accesses to an internal digital library of a fairly large company. The time-span of

acquired Web logs is 920 days. In this third case the user’s preferences are implicit

and collected on the server side, which implies the worst data quality for collaborative

ﬁltering (see Figure 1).

In contrast to EachMovie and Jester, Web logs ﬁrst needed to be extensively pre-

processed. Raw logs contained over 9.3 million requests. First, failed requests, redirec-

tions, posts, and requests by anonymous users were removed. We were left with slightly

over 1.2 million requests (14% of all the requests). These requests, however, still con-

tained images, non-content pages (such as index pages), and other irrelevant pages. Fur-

thermore, there were several different collections of documents in the corporate digital

library. It turned out that only one of the collections was relevant for the application of

collaborative ﬁltering. Thus, the amount of potentially relevant requests dropped dras-

tically. At the end we were left with only slightly over 20,500 useful requests, which is

0.22% of the initial database size.

The next problem emerged from the fact that we needed to map implicit preferences

contained in log ﬁles, into explicit ratings. As already explained, this is not a trivial task.

The easiest way to do this is to label items as 1 (accessed) or 0 (not accessed) as also

discussed in [2]. The downside of this kind of mapping is that it does not give any notion

of likes and dislikes. [3] have shown linear correlations between the time spent reading

a document and the explicit rating given to that same document by the same user (this

was already published by [10]). However, their test-users were using specialized client-

side software, which made the collected data more reliable (hence, in their case, we

talk about client-side implicit preferences). Despite this fact we decided to take reading

times into account when preprocessing Web logs.

We plotted reading times inferred from consecutive requests onto a scatter plot.

From that plot we noticed that the area indicating around 24 hours reading time is

very dense. We interpret these as the last accesses of a day, when the users went home

and logged in again the next day, which resulted in approximately 24-hour “reading”

time. Below the 24-hour line, there is a gap at approximately 10-hour reading time. We

decided to use this gap to deﬁne outliers – accesses above the gap are clearly outliers.

We decided to map reading times onto a discrete 3-score scale (scores being 1=“not

interesting”, 2=“interesting”, and 3=“very interesting”). Somewhat ad-hoc (intuitively)

we deﬁned two more boundaries: one at 20 seconds and another at 10 minutes. Since

items were research papers and 20 seconds is merely enough to browse through the

abstract, we decided to label documents with reading times below 20 seconds as “not

interesting”. Documents with reading times between 20 seconds and 10 minutes were

labelled as “interesting” and documents with reading times from 10 minutes to 10 hours

were labelled as “very interesting”. The previously deﬁned outliers were included due

to the lack of data. In the ﬁrst scenario they were labelled as “very interesting” and in the

second one as “interesting”. Since we had no reliable knowledge about the outliers, the

second scenario should have minimized the error we made by taking them into account.

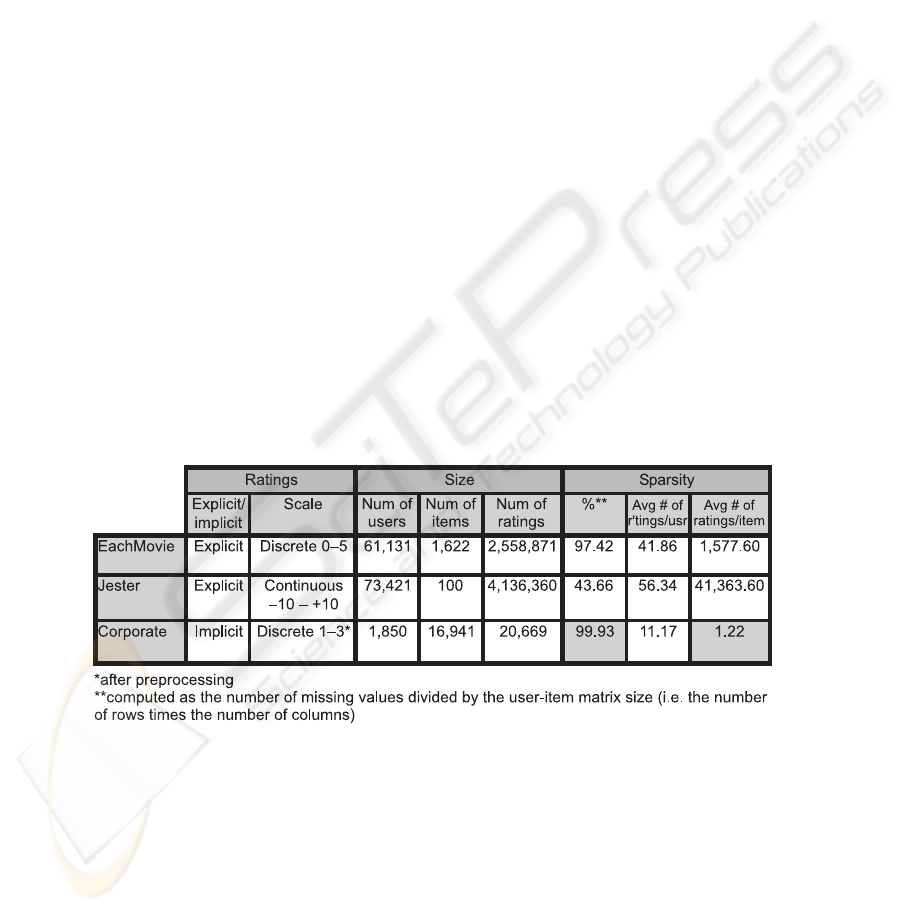
Table 1 shows the data characteristics of the three datasets. It is evident that a low

number of requests and somewhat ad-hoc mapping onto a discrete scale are not the

biggest issues with our corporate dataset. The concerning fact is that the average number

of ratings per item is only 1.22, which indicates extremely poor overlapping. Sparsity is

consequently very high, 99.93%. The other two datasets are much more promising. The

most appropriate is the Jester dataset with very low sparsity, followed by EachMovie

with higher sparsity but still relatively high average number of ratings per item. Also,

the latter two contain explicit ratings, which means that they are more reliable than the

corporate dataset (see also Figure 1).

Table 1. The data characteristics for the three datasets showing the kind of rating (explicit, im-

plicit), size of the dataset and the level of sparsity.

6 Experimental setting

We ran a series of experiments to see how the accuracy of collaborative ﬁltering recom-

mendations differs between the three datasets (from EachMovie and Jester we consid-

ered only 10,000 randomly selected users to speed up the evaluation process). Ratings

from each user were partitioned into “given” and “hidden” ratings according to the “all-

but-30%” evaluation protocol. The name of the protocol implies that 30% of all the

ratings were hidden and the remaining 70% were used to form neighborhoods.

We applied three variants of memory-based collaborative ﬁltering algorithms: (i) k-

Nearest Neighbors using the Pearson correlation (kNN Pearson), (ii) k-Nearest Neigh-

bors using the Cosine similarity measure (kNN Cosine), and (iii) the popularity pre-

dictor (Popularity). The latter predicts the user’s ratings by simply averaging all the

available ratings for the given item. It does not form neighborhoods and it provides

each user with the same recommendations. It serves merely as a baseline when evaluat-

ing collaborative ﬁltering algorithms (termed “POP” in [2]). For kNN variants, we used

a neighborhood of 120 users (i.e. k=120), as suggested in [5]. We decided to evaluate

both variants of the corporate dataset (the one where the outliers were labelled as “very

interesting”, referred to as “1/2/3/3”, and the one where the outliers were labelled as

“interesting”, referred to as “1/2/3/2”).

For each dataset-algorithm pair we ran 5 experiments, each time with a different

random seed (we also selected a different set of 10,000 users from EachMovie and Jester

each time). When applying collaborative ﬁltering to the variants of the corporate dataset,

we made 10 repetitions (instead of 5) since these datasets were smaller and highly

sparse, which resulted in less reliable evaluation results. Thus, we ran 90 experiments

altogether.

We decided to use normalized mean absolute error (NMAE) as the accuracy evalu-

ation metric. We ﬁrst computed NMAE for each user and then we averaged it over all

the users (termed “per-user NMAE”) (see [8]). MAE is extensively used for evaluating

collaborative ﬁltering accuracy and was normalized in our experiments to enable us to

compare evaluation results from different datasets.

7 Evaluation of results

Our evaluation of experimental results are shown in Figure 4. It can be seen that kNN

Cosine signiﬁcantly outperforms kNN Pearson on EachMovie dataset (we used two-

tailed paired Student’s t-Test with signiﬁcance 0.05 to determine if the differences in

results are statistically signiﬁcant). However, in the case of Jester, which has the small-

est degree of sparsity, kNN Pearson slightly, yet signiﬁcantly outperforms kNN Cosine.

On both these two datasets the two variants of a kNN algorithm signiﬁcantly outperform

Popularity. For both variants of the corporate dataset, on the other hand, kNN Cosine

signiﬁcantly outperforms kNN Pearson. In the ﬁrst scenario (i.e. with the 1/2/3/3 map-

ping), the difference between applying kNN Cosine and Popularity is statistically in-

signiﬁcant. For the second scenario (i.e. with the 1/2/3/2 mapping), our intuition proves

to be right – NMAE values are generally lower than in the ﬁrst scenario. However, this

time Popularity outperforms both kNN algorithms. Evaluation results from the corpo-

rate datasets show that predictions are less accurate and that NMAE value is relatively

unstable (hence the larger error bars showing standard deviations of NMAE values).

The main reason for this is low/no overlapping between values (i.e. extremely high

sparsity), which results in inability to make several predictions.

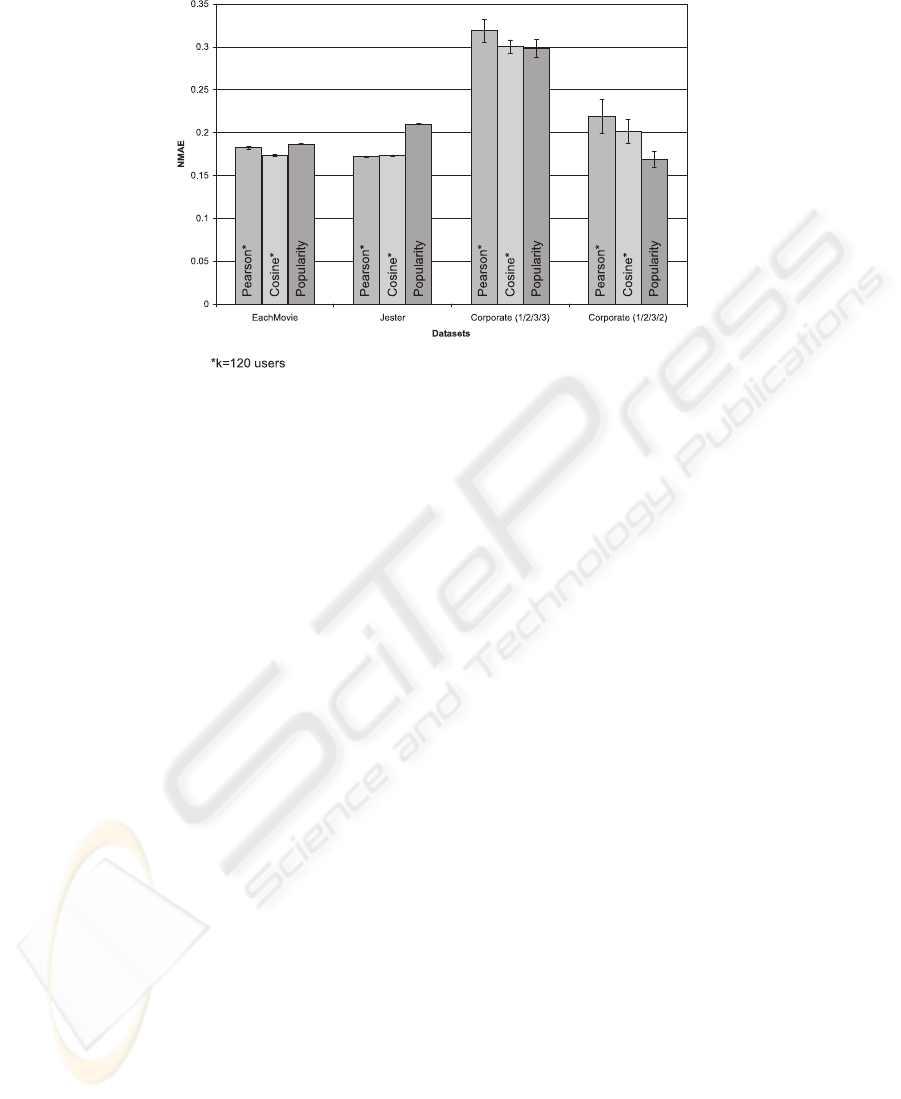
Fig.3. The results of experiments.

8 Discussion and future work

We have proposed a way to characterize the data used in collaborative ﬁltering to indi-

cate its quality in the light of collaborative ﬁltering performance. Our experiemnts have

conﬁrmed that high sparsity of the used corporate dataset resulted in unstable perfor-

mance. Before we will really be able to evaluate collaborative ﬁltering algorithms on

the given corporate dataset, we will need to reduce its sparsity. One idea is to apply LSI

(latent semantic indexing) [4] or to use pLSI (probabilistic latent semantic indexing)

[9] to reduce the dimensionality of the user-item matrix, which consequently reduces

sparsity. Another idea, which we believe is even more promising in our context, is to

incorporate textual contents of the items. There were already some researches done on

how to use textual contents to reduce sparsity and improve the accuracy of collabora-

tive ﬁltering [11]. Luckily we are able to obtain textual contents for the given corporate

dataset.

What is evident from our experiments is that mapping implicit into explicit ratings

has great inﬂuence on the evaluation results. Since the mapping was done somewhat ad-

hoc, we can not assure that the results are valid and that the users will be statisﬁed with

the recommendations. This needs to be investigated in greater depth. Also interesting,

the Cosine similarity works just as well as Pearson on EachMovie and Jester. Early

researches show much poorer performance of the Cosine similarity measure [2].

As a side-product we noticed that the true value of collaborative ﬁltering (in general)

is shown yet when computing NMAE over some top percentage of eccentric users.

We deﬁned eccentricity intuitively as MAE (mean absolute error) over the overlapping

ratings between “the average user” and the user in question (greater MAE yields greater

eccentricity). The average user was deﬁned by averaging ratings for each particular

item. This is based on the intuition that the ideal average user would rate every item with

the item’s average rating. The incorporation of the notion of eccentricity can give the

more sophisticated algorithms a fairer trial. We computed average per-user NMAE only

over the top 5% of eccentric users. The power of the kNN algorithms over Popularity

became even more evident. In near future, we will deﬁne an accuracy measure that

will weight per-user NMAE according to the user’s eccentricity, and include it into our

evaluation platform. We will also consider ways of handling the more eccentric users

differently.

References

1. BALDI, P., FRASCONI, P., and SMYTH, P. (2003): Modelling and Understanding Human

Behavior on the Web. In: Modelling the Internet and the Web, ISBN: 0-470-84906-1, 171–

209.

2. BREESE, J.S., HECKERMAN, D., and KADIE, C. (1998): Empirical Analysis of Predictive

Algorithms for Collaborative Filtering. In: Proceedings of the 14th Conference on Uncer-

tainty in Artiﬁcial Intelligence.

3. CLAYPOOL, M., LE, P., WASEDA, M., and BROWN, D. (2001): Implicit Interest Indica-

tors. In: Proceedings of IUI’01.

4. DEERWESTER, S., DUMAIS, S.T., and HARSHMAN, R. (1990): Indexing by Latent Se-

mantic Analysis. In: Journal of the Society for Information Science, Vol. 41, No. 6, 391–407.

5. GOLDBERG, K., ROEDER, T., GUPTA, D., and PERKINS, C. (2001): Eigentaste: A Con-

stant Time Collaborative Filtering Algorithm. In: Information Retrieval, No. 4, 133–151.

6. GRCAR, M. (2004): User Proﬁling: Collaborative Filtering. In: Proceedings of SIKDD 2004

at Multiconference IS 2004, 75–78.

7. GRCAR, M., MLADENIC D., GROBELNIK, M. (2005): Applying Collaborative Filtering

to Real-life Corporate Data. In: Proceedings of the 29th Annual Conference of the German

Classiﬁcation Society (GfKl 2005), Springer, 2005.

8. HERLOCKER, J.L., KONSTAN, J.A., TERVEEN, L.G., and RIEDL, J.T. (2004): Evaluat-

ing Collaborative Filtering Recommender Systems. In: ACM Transactions on Information

Systems, Vol. 22, No. 1, 5–53.

9. HOFMANN, T. (1999): Probabilistic Latent Semantic Analysis. In: Proceedings of the 15th

Conference on Uncertainty in Artiﬁcial Intelligence.

10. KONSTAN, J.A., MILLER, B.N., MALTZ, D., HERLOCKER, J.L., GORDON, L.R., and

RIEDL, J. (1997): GroupLens: Applying Collaborative Filtering to Usenet News. In: Com-

munications of the ACM, Vol. 40, No. 3, 77–87.

11. MELVILLE, P., MOONEY, R.J., and NAGARAJAN, R. (2002): Content-boosted Collabo-

rative Filtering for Improved Recommendations. In: Proceedings of the 18th National Con-

ference on Artiﬁcial Intelligence, 187–192.

12. RESNICK, P., IACOVOU, N., SUCHAK, M., BERGSTROM, P., and RIEDL, J. (1994):

GroupLens: An Open Architecture for Collaborative Filtering for Netnews. In: Proceedings

of CSCW’94, 175–186.