AN IMPROVED GENETIC ALGORITHM FOR SOLVING THE

VEHICLE ROUTING PROBLEM WITH TIME WINDOWS

Tao-Shen Li

School of Computer ,Electronics and Information, Guangxi University,Daxue Load 100, Nanning 530004, P. R. China

Jing-Li Wu

School of Mathematics and Computer, Guangxi Normal University, Guilin 541004, P. R. China

Keywords: Vehicle routing problem with time windows; Genetic algorithm; Crossover operator; Routing; heuristics.

Abstract: Many practical transport logistics and distribution problems can be formulated as the vehicle routing

problem with time windows (VRPTM). The objective is to design an optimal set of routes that services all

customers and satisfies the given constraints, especially the time window constraints. The complexity of

the VRPTW requires heuristic solution strategies for most real-life instances. However, the VRPTM is a

combination optimization problem and is a NP-complete problem, so we can’t get satisfying results when

we use exact approaches and normal heuristic ones. In this paper, an improved genetic algorithm to solve

the VRPTM problem is developed, which use an improved Route Crossover operator (RC’) and can meet

the needs for solving VRPTM problem. Computational experiments show that the GA based on RC’ can

obtain a general optimality for all evaluated indexes on the premise of satisfying every customer’s demand

and its performance is superior to the GA based on PMX or RC.

1 INTRODUCTION

Many practical transport logistics and distribution

problems can be formulated as the vehicle routing

problem with time windows (VRPTM) which

objective is to obtain a minimum-cost route plane

serving a set of customers with known demands.

Each customer is assign to exactly one vehicle route

and the total demand of any route must not exceed

the vehicle capacity. In addition, a time window is

associated with each customer defining an interval

wherein the customer has to be supplied. Specific

examples of VRPTM include bank deliveries, postal

deliveries and situations where the customer must

provide access, verification, or payment upon

delivery of the product or service (Solomon and

Desrosiers, 1991).

The VRPTM is a NP-complete problem (Lenstra

and Rinnooy, 1981). Due to the intrinsic difficulty of

the problem, search methods based on heuristics are

most likely applied to solve practical size problems.

Heuristic methods often obtain optimum or near

optimum solutions for large problems in rational

computing time. Therefore, during the last decades

much effort has been devoted to the development of

powerful heuristic algorithm (Savelsbergh, 1985)

(Koskosidis, et. al 1992) (Desrosiers, et. al 1992)

(Fisher, et. al 1997) (Kohl and Madsen, 1997)

(Russel, 1995).

The Genetic Algorithm (GA) is an adaptive

heuristic search method based on population genetic.

The basic concepts were primarily developed by

Holland (Holland, 1975). The practicality of using

the GA to solve complex problem is demonstrated in

(DeJong, 1980) (Grefenstette, 1986) (Goldberg,

1989). The GA tries to develop a viable solution for

an optimization problem through the successive

evolution of solutions that don’t meet a criterion. It

mimic the process of biological evolution where,

over successive generations, individuals who adapt

to the environment best live on and reproduce, while

other individuals die off (Mitchell and Forrest,

1993). Eventually, over many generations, the group

has been optimized and only individuals who adapt

to the environment mostly survive.

143

Li T. and Wu J. (2005).

AN IMPROVED GENETIC ALGORITHM FOR SOLVING THE VEHICLE ROUTING PROBLEM WITH TIME WINDOWS.

In Proceedings of the Second International Conference on e-Business and Telecommunication Networks, pages 143-149

DOI: 10.5220/0001415101430149

 SciTePress

Many efficient methods to use GA heuristic for

solving the VRPTM have been proposed recently

(Bräysy, 2001). Thabgiah describes a method called

GIDEON (Thangiah, et. al 1995) (Thangiah,

1995).Potvin and Bengio propose a genetic

algorithm GENEROUS that applies genetic

operators to solutions (Potvin and Gengio, 1996).

Berger et al present a approach based on the

hybridization of a GA with well-known construction

heuristics (Berger, et. al 1998). Homberger and

Gehring propose two evolutionary strategies for

solving the VRPTM (Homberger and Gehring,

1999). Bräysy presents a comprehensive sensitivity

analysis of the main components of the genetic

algorithm in the VRPTW context by proposing

several new crossover and mutation operators,

testing different forms of genetic algorithms,

selection schemes, scaling schemes, and the

significance of the initial solutions (Bräysy, 1999).

In (Bräysy, 2000), Bräysy describes a two-phase

hybrid evolutionary algorithm based on the

hybridization of a GA and an evolutionary algorithm

consisting of several local search and route

construction. Ombuki, Nakamura and Osamu

present a hybrid search based on genetic algorithms

and tabu search for vehicle routing (Ombuki, et.al

2003).

In this paper, we proposed an improved genetic

algorithm based on improved Route Crossover (RC’)

to solve the VRPTM, which ensures to satisfy every

customer’s demand. its performance is superior to

existing methods based on PMX

or Route

Crossover (RC) (Davis, 1991)

The remainders of this paper are organized as

follows. In Section 2, we present the mathematical

model of VRPTM. In Section 3, a heuristic method

for solving VRPTM will be developed based on the

principle of GA. The computational experiments will

be presented in Section4, and Section 5 will conclude

the paper.

2 MATHEMATICAL MODEL

The VRPTM consists of a large number of customers.

Each customer has a known demand level, which

must be supplied from a single depot. Delivery

routes for vehicles are required, start and finish at the

depot, so that all customers’ demands are satisfied

and each customer is visited just by one vehicle.

Each vehicle capacities and its maximum distance

that it can travel are given previously. A vehicle

may arrive before the beginning of the time window

and wait without cost until service is available.

However, no vehicle may arrive past the closure of a

given time interval. So the mathematical model of

the VRPTM problem is formulated as follows:

VRPTM

Min

()

servicenoIdtCovDis _+++

(2.1)

Dis=

∑

∈∈ ∈VkNiNj

ijkij

(2.2)

Cov=

∑

∈Vk

(2.3)

Idt=

∑∑

∈∈VkNi

(2.4)

Subject to:

)5.2(VkqXd k

CiNj

ijki

∈∀≤

∑

∈∈

)6.2(VkDXc k

NiNj

ijkij

∈∀≤

∑

∈∈

)7.2(1 CiX

VkNj

ijk

∈∀=

∑

∈∈

)8.2(1

VkX

∈∀=

∑

∈

)9.2(,0 VkChXX

hjk

ihk

∈∀∈∀=−

∑

∈∈

)10.2(1

VkX

∈∀=

∑

∈

(

)

)11.2(,,1 VkNjisXKte

jkijkijik

∈∀∈∀≤−−+

)12.2(, VkNibsa

iiki

∈∀∈∀≤≤ 　　

}{

)13.2(,,1,0 VkNjiXZ

ijkk

∈∀∈∀∈，

if the vehicle k travels directly from i to j

ijk

otherwise (2.14)

1, if vehicle k is used

otherwise (2.15)

where

V =a set of vehicles

C =a set of geographically dispersed customers

N =C and 0 (0 denotes the central depot)

=cost per unit amount transported from source i

to destination j

=travel time between source i and destination j

=maximum capacity of vehicle k

=maximum travel distance permitted for

ICETE 2005 - GLOBAL COMMUNICATION INFORMATION SYSTEMS AND SERVICES

144

vehicle k

=cost of vehicle k once it is used

=demander of customer i

=earliest time allowed for delivery to customer i

(the minimum of time window)

=lastest time allowed for delivery to customer i

(the maximum of time window)

=waiting time of vehicle k at customer i when

it arrives before a

no_service =number of customers not served

=time of vehicle k starting visiting customer i ,

=time of vehicle k finishing visiting customer i ,

= e

-s

Our objective is to minimize the total distance

for each vehicle to travel, the cost used by each

vehicle, the waiting time wasted to meet the

demands of all the customers (2.1) without breaking

the constraints of vehicle capacity, travel distance

and arrival time. Thus, this problem can be treated as

a multi-objective optimization problem. A feasible

solution for the VRPTM is to serve all the customers

without vehicle exceeding its maximum capacity

(2.5) or its maximum travel distance (2.6). In

addition, each customer can be served by one and

only one vehicle (2.7). Constraints (2.8), (2.9) and

(2.10) ensure that each vehicle starts from the depot

and returns to it after finishing visit. The constraint

(2.11) ensures that vehicle k can’t arrive at

destination j before time e

when it drives from

source i to destination j, and K is a relative large

scalar quantity. The constraint (2.12) enforces the

arrival time of a vehicle at a customer site to be

between the customers’ earliest and latest arrival

time.

3 AN IMPROVED GENETIC

ALGORITHM FOR VRPTM

3.1 General Explanation

A GA is directly derived from the behavior of genes

and chromosomes in nature. Each ‘generation’, or

family of possible solutions, is made up of a set of

strings or ‘chromosomes’. Each chromosome is in

turn made up of individual ‘genes’. These genes are

codes of designing variables that are used to

evaluate the function being optimized. The GA calls

a subroutine to compute the fitness value or

normalized objective value for each chromosome in

a population. These values are evaluated and

compared with each other. Those chromosomes

having the best values ‘survive’ and are passed on to

the next generation. In each generation, there is a

small probability for each chromosome to mutate (or

change) in one or more positions in the string (gene).

There is a different probability that two strings will

mate or crossover to produce a child. The children

and mutations are placed into the next generation.

The process of mutation, crossover, evaluation and

reproduction are repeated until it is convergent to a

suitable ‘solution’ for the problem.

In following sections, we will introduce how we

apply the genetic algorithm to the VRPTM.

3.2 Chromosome Representation

When we use the GA to solve VRPTM, designing a

kind of chromosome representation for solution

space is first problem to need solving. Here we

represent each chromosome as a sequence of a set of

vehicle route. A route is composed of a sequence of

nodes (customers). For example, the chromosome: 1

5 2 4 3 6 8 7 is composed of three routes r1: D C1

C5 C2 D and r2: D C4 C3 C6 D and r3: D C8 C7 D

(D denotes central depot, C denotes customer). The

routing scheme given in reference (Ombuki, et. al

2003) is used to transform each chromosome into a

set of routes.

3.3 Selection Operator

We use Roulette Wheel Selection to generate a new

population for the next generation. Roulette Wheel

Selection is an elite model which can ensure that the

best individual can be preserved into the next

generation.

3.4 Improved Crossover Operator

Since some customers may not be served when the

Route Crossover (RC) (Davis, 1991) is used to solve

VRPTM, we proposed the improved Route

Crossover (RC’), which is an improvement of RC. It

can optimize the problem on the premise of

satisfying every customer’s demand. RC’ operation

is presented as the following steps:

(1) Transform two parent chromosomes, P1 and

P2, into two clusters of routes by the routing scheme

mentioned above.

AN IMPROVED GENETIC ALGORITHM FOR SOLVING THE VEHICLE ROUTING PROBLEM WITH TIME

WINDOWS

145

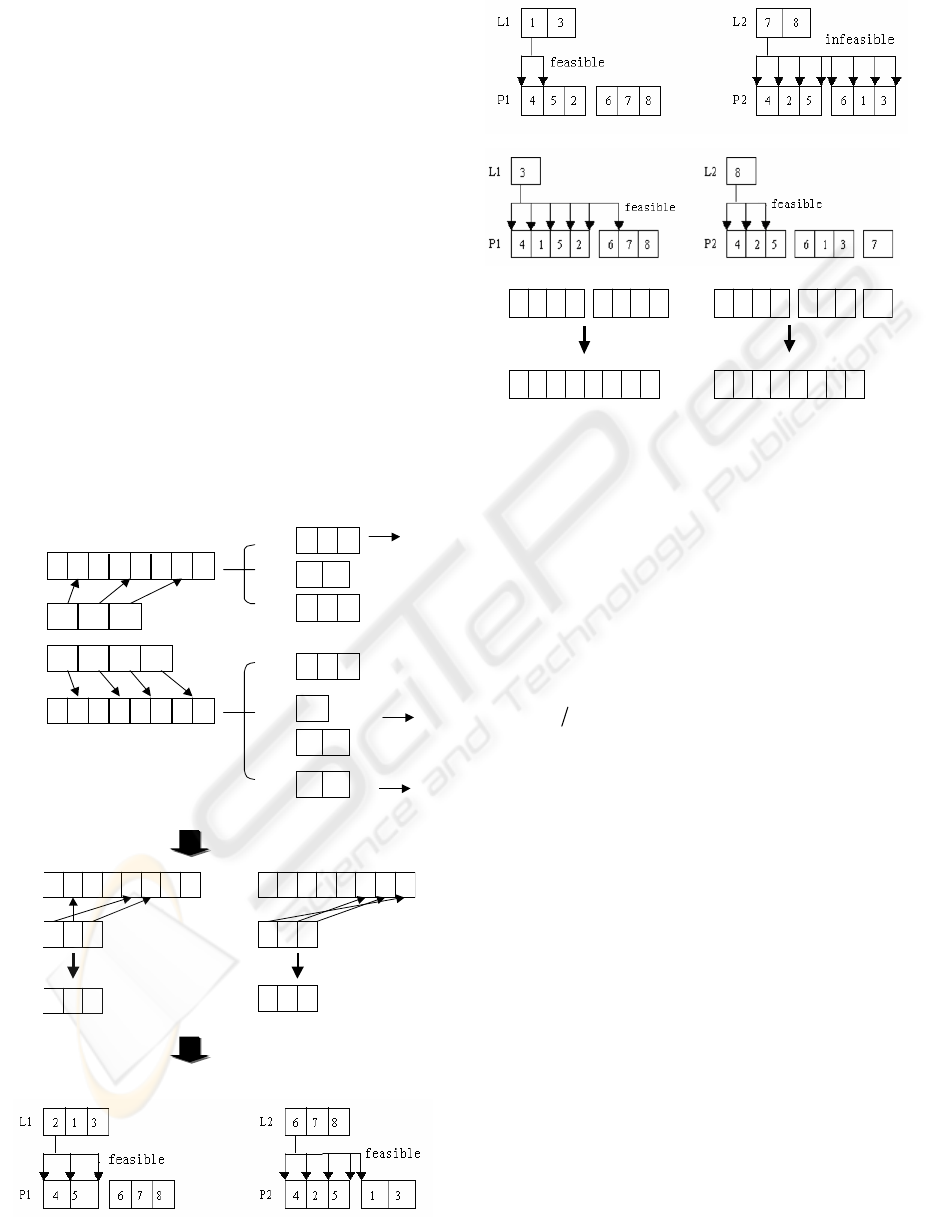
(2) A binary mask-pattern is generated

randomly for each cluster of routes, whose length is

equal to the number of the routes. One bit of the

mask pattern corresponds to one route in the cluster

of routes.

(3) Considering one parent Pi (i=1,2), the

contents of the route(s) corresponding to a “1” in the

mask pattern are copied directly to its offspring. The

customers of the routes equivalent to “0” in the mask

pattern are sorted out to form a list in the order of

the appearance in its crossing parent Pj (j=1,2, j ≠ i).

(4) Considering the list in (3), each of the

customers from the list is inserted according to their

order of appearance to the first feasible position in

the upcoming route represented by its respective

offspring. The steps above are almost the same as

RC, the only difference between the two operators is

that if a customer can’t be inserted into any existent

route, it will be declared as a non-served customer

and will not be assigned to any route in RC.

However in RC’, a new route will be generated and

the customer will be inserted into it as well.

Figure 1: Improved Route Crossover(RC’) operator

3.5 Design of the fitness function

The fitness function measures how “good” a

chromosome is, so that better chromosomes can be

selected for mating. Because each chromosome

represents a viable solution of VRPTM problem, we

need to make an estimate of the results that be

obtained after optimizing routes。In this paper, the

fitness function of an individual is as follows

()

servicenoIdtCovDisF _1 ⋅

+⋅

+⋅α=

Where α,β,γ,μ are weight parameters associated with

the total traveled distance, the cost used by vehicles,

the waiting time and the number of customers not

served respectively. The weight values of the

parameters used in this function were determined

empirically and set asα=0.001, β=1.0,γ=0.001,μ=1.0.

The evaluation function is implemented after

converting each of the chromosomes into a set of

feasible routes.

4 EXPERIMENT AND ANALYSIS

The algorithm described in the previous section and

HG1 proposed in (Homberger and Gehring, 1999)

are coded in visual C++ 6.0, and executed using a

machine with Pentium 2.0G CPU.

Considering a problem with 10 customers and a

central depot, all the customers’ characteristics and

demands are given in table 1. The distances between

the central depot and the customers are given in

4 2 5 8 1 3 6 7

1 2 3 4 5 6 7 8

1 2 3 L1 8 6 7 L2

2 1 3 L1

Sort

6 7 8

Sort

P2P1

4 1 5

6 3 7 8 6 1 3 7 4 2 8 5

C1 4 1 5 2 6 3 7 8 C2 4 2 8 5 6 1 3

1 2 3 4 5 6 7 8

4 2 5 8 1 3 6 7

M1 0 1 1

M2 1 0 1 0

1 2 3

4 5

6 7 8

4 2 5

1 3

6 7

ICETE 2005 - GLOBAL COMMUNICATION INFORMATION SYSTEMS AND SERVICES

146

table 2. Assuming a vehicle’s capacity is 8 tons and

speed is 50km/h, then the travel time from source i

to destination j is d

/50(h), and the travel cost

between them is assumed as d

. In first line of table

1, zero(i=0) represents the central depot, a

represents the earliest time to move away from

central depot, b

represents last time restriction to

return central depot.

We apply the improved genetic algorithm based

on RC’ and HG1 to solve the above problem, the

population size is set at 20, dynamic crossover

probability is used. After 100 generations, 3 vehicle

routes are needed in all:

Our algorithm:

first vehicle route: 0→4→10→7→0

second vehicle route: 0→6→2→3→0

third vehicle route: 0→9→5→1→8→0

total distance: 437.0 (km)

HG1:

first vehicle route: 0→2→10→0

second vehicle route: 0→9→5→1→8→0

third vehicle route: 0→6→7→4→3→0

total distance: 734.0 (km)

Considering all the customers’ characteristics and

demands are given in table 3, distance and other

situation is kept constant. After 100 generations, the

experimental results of our algorithm and HG1 are

same. 5 vehicle routes are needed in all:

first vehicle route: 0→5→2→3→0

second vehicle route: 0→6→8→0

third vehicle route: 0→4→9→0

fourth vehicle route: 0→1→7→0

fifth vehicle route: 0→10→0

total distance: 658.0 (km)

As can seen from results above, the improved

genetic algorithm based on RC’ was better than HG1

in some situation.

Apparently, this is a feasible solution to this

problem, which satisfies both the constraints and

every customer’s demand. We also implement the

genetic algorithm based on RC for the same problem.

Though we still need 3 vehicles, customer 2 never

gets service. It indicates that RC’ operator is

superior to RC. In addition, under the same

circumstance, we traced the processes of the GAs

based on PMX, RC and RC’ respectively and found

that the best fitness and average fitness of RC’ were

better than those of PMX and RC, the results are

illustrated in Fig.2 and Fig.3. Considering two kinds

of population size of the problems, the results of

advanced experiment show that RC’ is still superior

to PMX and RC in other performances, which is

given in table 4.

first vehicle route: 0→4→10→7→0

second vehicle route: 0→6→8→3→0

third vehicle route: 0→9→5→1→0

Table 1: Customers’ Characteristics and Demands Table 2: Distances between the central depot and the customers (km)

Customer

i(ton)

(hour)

，b

]

(time)

0 0 0 [0，100]

1 3 2 [1.52，7]

2 4 2 [1.78，7]

3 3 1 [1.78，14]

4 3 1 [0.28，15]

5 2 2 [2.6，13]

6 1 2 [0.78，3]

7 1 2 [3.6，6]

8 3 2 [3.7，11]

9 1 2 [1.36，5]

10 4 1 [0.6，13]

0 1 2 3 4 5 6 7 8 9 10

0 0 76 89 89 14 130 39 180 185 68 30

1 157 0 82 176 35 113 142 80 105 94 137

2 185 140 0 40 178 138 180 66 171 126 18

3 1 200 43 0 83 129 142 43 196 66 107

4 190 121 85 120 0 15 159 182 34 65 1

5 128 2 1 46 103 0 142 31 75 45 28

6 141 117 16 16 170 30 0 45 29 150 193

7 1 14 194 80 85 85 164 0 60 187 4

8 85 6 48 152 107 79 4 82 0 113 91

9 21 30 80 127 53 31 32 110 49 0 185

10 46 162 123 14 87 35 132 34 10 106 0

AN IMPROVED GENETIC ALGORITHM FOR SOLVING THE VEHICLE ROUTING PROBLEM WITH TIME

WINDOWS

147

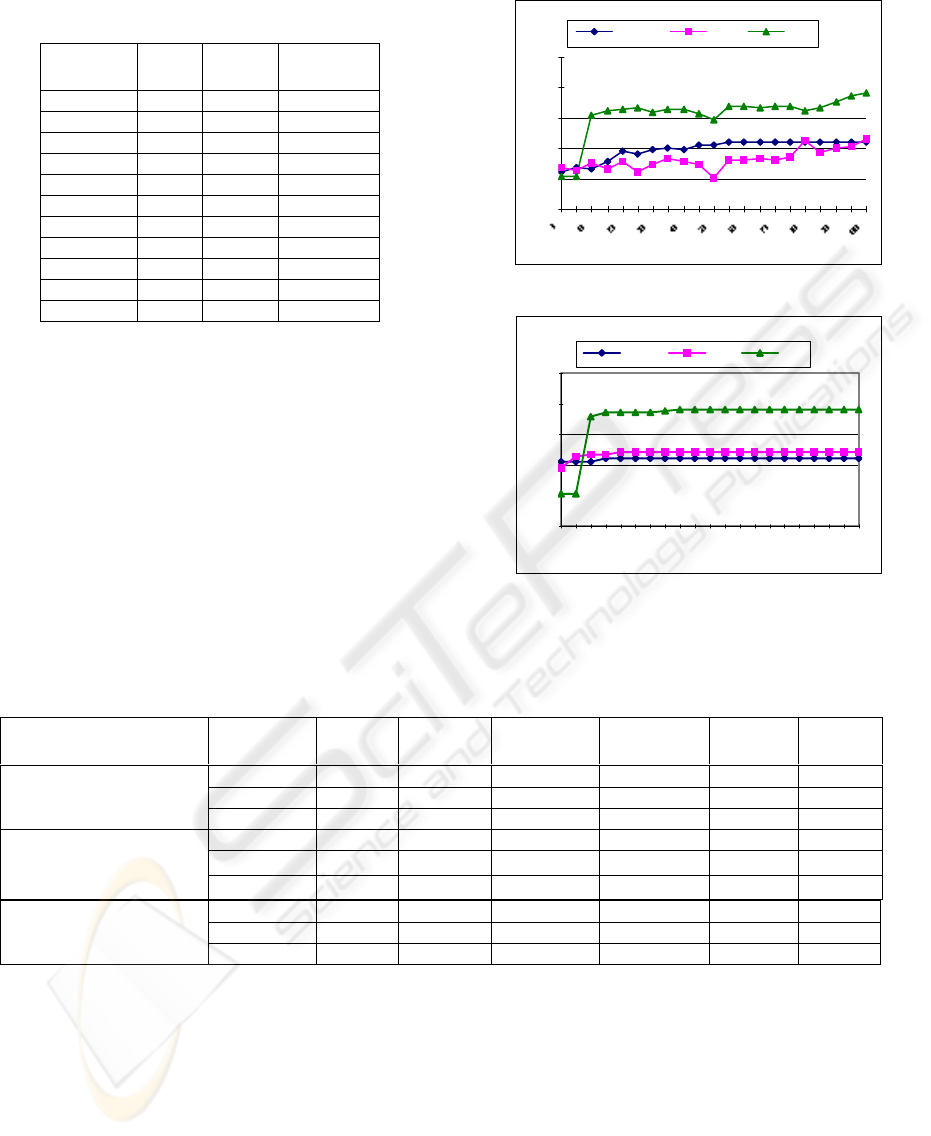
Table 3: Customers’ Characteristics and Demands

0,1

0,15

0,2

0,25

0,3

0,35

generatioin

average fitness

PMX RC RC'

Figure 2: Comparing average

0,1

0,15

0,2

0,25

0,3

0,35

0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100

generation

best fitness

PMX RC RC'

Figure 3: Comparing the best fitness

Table 4: Comparing the searching results using methods based on PMX, RC, RC’ respectively

5 CONCLUSION

Based on genetic algorithm, we constructed an

improved genetic algorithm using RC’ operator to

solve VRPTM problem. Experimental results show

that with the increasing size of a problem, this

algorithm can obtain general optimality for all

evaluated indexes on the premise of satisfying every

customer’s demand and its performance outperforms

PMX and RC. Compared with HG1, its performance

and speed are more effective.

Customer

i(ton)

(hour)

，b

]

(time)

0 0 0 [0，100]

1 3 2 [1.52，7]

2 4 2 [1.78，7]

3 3 1 [1.78，14]

4 3 1 [0.28，15]

5 2 2 [2.6，13]

6 1 2 [0.78，3]

7 1 2 [3.6，6]

8 3 2 [3.7，11]

9 1 2 [1.36，5]

10 4 1 [0.6，13]

PMX 0.019266 0.018823 10903.0 41 2.940 0

RC 0.022225 0.022081 9994.0 32 0.60 3

100

(70,200)

RC′ 0.034420 0.032051 7051.0 22 2.280 0

Problem size (population

size，generation)

crossover

operator

best

fitness

average

fitness

distance

number of

cars

sparing

time

no_

service

PMX 0.211238 0.211238 734.0 4 0.00 0

RC 0.220753 0.215167 529.0 3 0.96 1

(20,100)

RC′ 0.290899 0.290899 437.0 3 0.620 0

PMX 0.043584 0.043584 4944.0 18 0.30 0

RC 0.049735 0.049735 5104.0 15 2.50 0

(100,200)

RC′ 0.086816 0.086268 2518.0 9 0.660 0

ICETE 2005 - GLOBAL COMMUNICATION INFORMATION SYSTEMS AND SERVICES

148

REFERENCES

Ombuki, B. Nakamura, M. and Osamu, M., 2002 A

Hybrid search based on genetic algorithms and tabu

search for vehicle routing. In the 6th IASTED

International Conference on Artificial Intelligence and

Soft Computing, 176-181.

Davis L., 1991, Handbook of genetic algorithms. Van

Nostrand Reinhold.

Solomon, M. M., and Desrosiers, J., 1988, Time window

constrained routing and scheduling problem.

Transportation Science, 22(1):1--13

Lenstra, J. K., and Rinnooy Kan A. H. G., 1981,

Complexity of vehicle routing and scheduling

problems, Networks, 11,221—262.

Savelsbergh M.W.P., 1985, Local search for routing

problems with time windows. Annals of Operations

Research 4, 285-30.

Koskosidis, Yiannis, Warren B. Powell and Marius M.

Solomon, 1992, An optimization based heuristic for

vehicle routing and scheduling with time window

Constraints. Transportation Science, 26(2), 69-85

Desrosiers M. Desrosiers J.. Solomon M. M.,1992, A new

optimization algorithm for the vehicle routing problem

with time windows, Operation Research, 40,342--354

Fisher M. L., Jornsten K. O., and Madsen O. B. G.,1997,

Vehicle routing with time windows: two optimization

algorithm, Operation Research, 45,488--492

Kohl N., Madsen O.B.G., 1997, A optimization algorithm

for the vehicle routing problem with time windows

based on Lagrangian Relaxation, Operation Research,

40,342--354

Russel R. A., 1995, Hybrid heuristics for the vehicle

routing problem with time windows, Transportation

Science, 29(2):156—166

Holland J. H., 1975, Adaptation in natural and artificial

systems. University of Michigan Press, Ann Arbor.

DeJong, 1980, Adaptive system design: a genetic

approach, IEEE Transaction on Systems, Man and

Cybernetics,10(9):566--574

Grefenstette J. J., 1986, Optimization of control parameter

for genetic algorithms, IEEE Transactions on Systems,

Man and Cybernetics,16(1):122--128

Goldberg D., 1989, Genetic Algorithm in Search,

Optimization, and Machine Learning, Addison Wesley

Publishing Company Inc. New York

Mitchell M. and Forrest S.1993, Genetic Algorithms and

Artificial Life. [Online document],: http://

ww.santafe.edu/~mm/GA.Alife.ps

Bräysy O.2001 ， Genetic Algorithms for the Vehicle

Routing Problem with Time Widows, Internal Report

STF42 A01021, SINTEF Applied Mathematics,

Department of Optimisation, Norway.

Thangiah, S.R., I.H. Osman, R. Vinayagamoorthy and T.

Sun,1995, Algorithms for the Vehicle Routing

Problems with Time Deadlines, American Journal of

Mathematical and Management Sciences, 13,

323−355.

Thangiah, S. R., 1995, Vehicle routing with time windows

using genetic algorithms, in Application Handbook of

Genetic Algorithms: New Frontiers, Volume II, L.

Chambers (ed), 253−277, CRC Press

Potvin J. Y. and Gengio S., 1996,The vehicle routing

problem with time windows part II: genetic search.

INFORMS Journal on Computing, 8(2):165—172

Berger J., Salois M. and Begin R., 1998,A hybrid genetic

algorithm for the vehicle routing problem with time

windows. In Proceedings of the 12th Bienneal

Conference of the Canadian Society for

Computational Studies of Intelligence, Sringer-Verlag,

114--127

Homberger J. and Gehring H.,1999,Two evolutionary

meta-heuristics for the for the vehicle routing problem

with time windows, INFORMS Journal on Computing,

37(3):297--318

Bräysy, O. 1999, A new algorithm for the vehicle routing

problem with time windows based on the

hybridization of a genetic algorithm and routing

construction heuristics. In Proceedings of the

University of Vaasa, Research papers 227,

Bräysy, O., Berger J. and Barkaoui M.,2000, A new hybrid

evolutionary algorithm for the vehicle routing problem

with time windows, Presented at the Route

2000-Workshop, Skodsborg, Denmark

Table 4. Comparing the searching results using methods

based on PMX, RC, RC’ respectively

AN IMPROVED GENETIC ALGORITHM FOR SOLVING THE VEHICLE ROUTING PROBLEM WITH TIME

WINDOWS

149