Comparison of Time and Spectral Domain Features on

Postural Signals Utilizing Neural Networks

Andreas Fey, David Sommer, Martin Golz

FH Schmalkalden - University of Applied Sciences, Dptm. of CS,

Postfach 10 04 52, 98574 Schmalkalden, Germany

Abstract. Human postural equilibrium is the result of complex control

processes. Nevertheless these processes are taken for granted in our daily life,

disturbance or degeneration of a single system involved in these processes leads

to a variety of diseases, which pile up with age. Therefore, investigation of

postural signals is the aim of many clinical and biophysical studies, in order to

recognize diseases early and to improve the precision of diagnostics. In order to

analyze posturographic signals we conducted a pilot study to measure body

sway of nine healthy subjects during four trials with different acoustic and

visual impairments, in order to detect their influence on stance. Ten time

domain and five spectral domain feature extraction methods were applied on

segmented raw data and classified by five different classification methods. The

test errors were empirically minimized first by estimating best parameters for

each feature extraction method, yielding to an optimal combination of feature

extraction and classification methods. It turned out, that Burg autoregressive

method of power spectral density estimation and Optimized Learning Vector

Quantization was the best method combination. The classification task “no

impairment” versus “visual impairment”, i.e. “eyes open” versus “eyes closed”,

showed best discriminative performance indicated by mean test errors of 2.2%.

The pilot study pointed out, that the established biosignal analysis system

gained a high sensitivity on small postural influences.

1 Introduction

During erect standing several muscles are permanently contracted in order to stabilize

body sway and prevent the body from falling. The control mechanisms in the central

nervous system for these muscles are influenced by a multisensory input, subdivided

in the vestibular, proprioceptive and visual system [3]. Disturbances or degenerations

of only one of these systems lead to a variety of diseases, including falls, Ménière’s

disease, cerebellar degeneration or uni- and bilateral vestibular malfunction. The

annual costs associated with falls are exceeded only by motor vehicle injuries [11].

Many clinical and biophysical studies aimed therefore the investigation of postural

signals for early recognition of diseases and a more precise diagnostic. In order to

examine different states of equilibrium, usually a single system is stimulated or

disabled, e.g. the visual system by closing both eyes, the proprioceptive system by

Fey A., Sommer D. and Golz M. (2005).

Comparison of Time and Spectral Domain Features on Postural Signals Utilizing Neural Networks.

In Proceedings of the 1st International Workshop on Biosignal Processing and Classiﬁcation, pages 42-49

DOI: 10.5220/0001196100420049

 SciTePress

adding vibratory stimuli at the calf muscles or the vestibular system by applying tones

at the ear.

Auditory stimuli is a wide spread method to provoke the vestibular system, and is

used for this reason since the 30s. The mechanisms underlying this effect are not fully

understood. Some authors assume sound giving rise to contractions of middle-ear

muscles resulting in excessive jerking of the stapes and causing movements of the

perilymph in semicircular canal system [14]. In the 80s and 90s some studies

examined the influence of various frequencies and loudness on postural sway, and

showed that varying frequencies have a primary effect on antero-posterior sway,

while changing the loudness results in medio-lateral sway. Different frequencies seem

to have a stabilizing or destabilizing effect as well [17]. Another variation in acoustic

stimulation beside frequency and loudness is the continuity of the tones. Even in 1929

Thullio showed, that tones intended on only one ear provoke symptoms like sway or

nystagmus, while binaural stimulations preserve this effect. Interrupted tones

additionally increase this effect [6]. At least the direction of the tones was also

examined resulting in greater effects of moving auditory stimuli compared to

stationary auditory stimuli [17][16].

In order to estimate the sensitivity of postural sway measures on small and on

serious influences we conducted a pilot study including nine healthy subjects. As an

example of serious influences we selected visual impairments by occluding the eyes

and therefore interrupting visual feedback. Binaural presented moving acoustic

stimuli served as small influences.

Based on a literature inquiry of the last decade, ten important time domain and five

spectral domain feature extraction methods were established. Performance analysis

utilizing Neural Networks was carried out.

2 Methods

Postural sway of nine healthy volunteers without known visual, proprioceptive or

vestibular diseases was measured in four trials of different modalities with / without

interruption of visual feedback (00 / 10) and with / without binaural stimulation (00 /

01 / 02):

1. eyes open, normally illuminated environment, no auditive stimuli (00)

2. eyes closed and occluded , fully darkened environment, no auditive stimuli (10)

3. eyes closed and occluded, fully darkened environment, periodic randomized noise

from left to right ear of one second length (11)

4. eyes closed and occluded, fully darkened environment, periodic randomized noise

from left to right ear of 2.5 second length (12)

Symbol “0” stands for no impairment, while symbol “1” and “2” stand for

impairment. The first symbol concerns visual, the second acoustic impairments. Each

trial of 100 second duration was followed by a recovery time of one minute and

additionally by one minute for darkness adaption after the first trial.

Recordings of postural sway were performed on a force platform on which subjects

had to stand upright. Signals of four force sensors located under the platform were

sampled with a rate of 1000 sec

-1

and were subsequently processed to calculate two

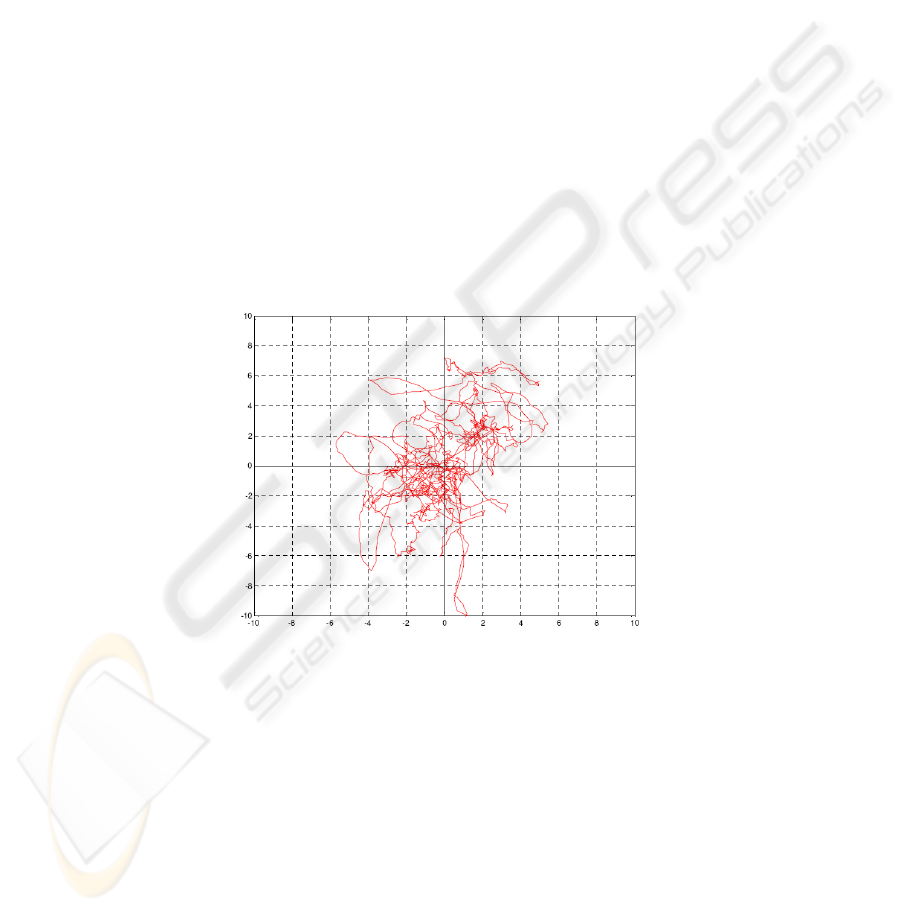
dimensional vectors of locations of the center-of-foot-pressure (COP). The time series

of COP visualized in medio-lateral and antero-posterior direction as y- and x-axis

respectively is called stabilogram (figure °1).

Because the classification methods used here require lots of data for learning to

raise the generalization effect, although stationarity of the signal is required for

following methods, we segmented the raw data and estimated the optimal segment

length empirically. While a short segment length would raise the quantity of data,

long segments would improve the spectral resolution and therefore improve the

quality of results of the spectral domain features.

15 different feature extraction methods (table °1) of time and spectral domain

which were commonly used by several authors in the last two decades were applied

than to the segmented data. Spectral power density (PSD) was computed by spectral

domain features. Subsequently PSDs were averaged in frequency bands because of

the resulting large amounts of components and because of their high variances, which

are typical for biomedical signals as realizations of random processes. The adjustable

parameters for the spectral domain feature extraction methods are therefore lower and

upper cut-off frequency f

and f

respectively and the band width ∆f. The range

between f

and f

is equidistant divided with step size ∆f. For Burg and MTM

additionally another parameter (model order / time-bandwidth product [15]) was

empirically computed. Band averaged PSDs were then used as components of input

vectors for all classification methods.

Fig. 1. Stabilogram of one subject. Time series of medio-lateral (x) and anterior-posterior (y)

components of Centre-of-Pressure measured in upright standing with opened eyes; duration:

100 sec, sampling rate: 1,000 sec

-1

All ten time-domain methods plus the total spectral energy resulted in 23 different

features. Because each feature would be to less data for the classification methods, all

of them were combinated to a 23 dimensional input vector. Each possible

combination (2²³ combinations = 8.388.608 possibilities) was applied to the

classification methods to evaluate the best classifiable input vector of time domain

features empirically.

[mm]

Table 1. Utilized feature extraction methods in time and spectral domain with references to

authors using this methods in the last decade

Time domain Spectral domain

Sway path [17] [12] [1] Sway area [17] [12] [1] Periodogram (PSD) [15]

Root mean squares [1] Amplitudes of COP [17] Welch Overlapped Segments

Analysis (PSD) [15]

Mean [17] Maximal displacement [17] Burg autoregressive method

(PSD) [15]

Standard deviation [17] Stabilogram diffusion plot

[1]

Multitaper Method (PSD) [15]

Sway velocity [17] Sway density curve [2] Total spectral energy [12] [1]

The test error was computed using the leave-one-out (LOO) cross-validation. LOO

estimates this error by removing sequentially one sample from the training samples,

using the remaining samples for training and leading to a classification rule, which is

tested on the held-out example [7]. LOO leads to a high computational cost (n-1

repetitions for n samples), but is an almost unbiased estimator of the true error.

At least we compared the following classification methods empirically by taking

test errors estimated by LOO into account:

1. Learning Vector quantization (LVQ), with variants [8]

2. Self Organizing Maps (SOM) [9]

3. Growing Cell Structures (GCS) [5]

4. Support Vector Machine (SVM) [18]

3 Results

3.1 Parameter optimization by empirical error minimization

The following examinations were carried out to find optimal parameters in all steps of

the classification process and therefore minimize the empirical error. OLVQ

classification method was used because of its fast convergence properties. 00 vs. 10,

the typical “eyes open” versus “eyes closed” combination, examined by most authors

(eg. [2], [4]) in posturographic studies, was tested.

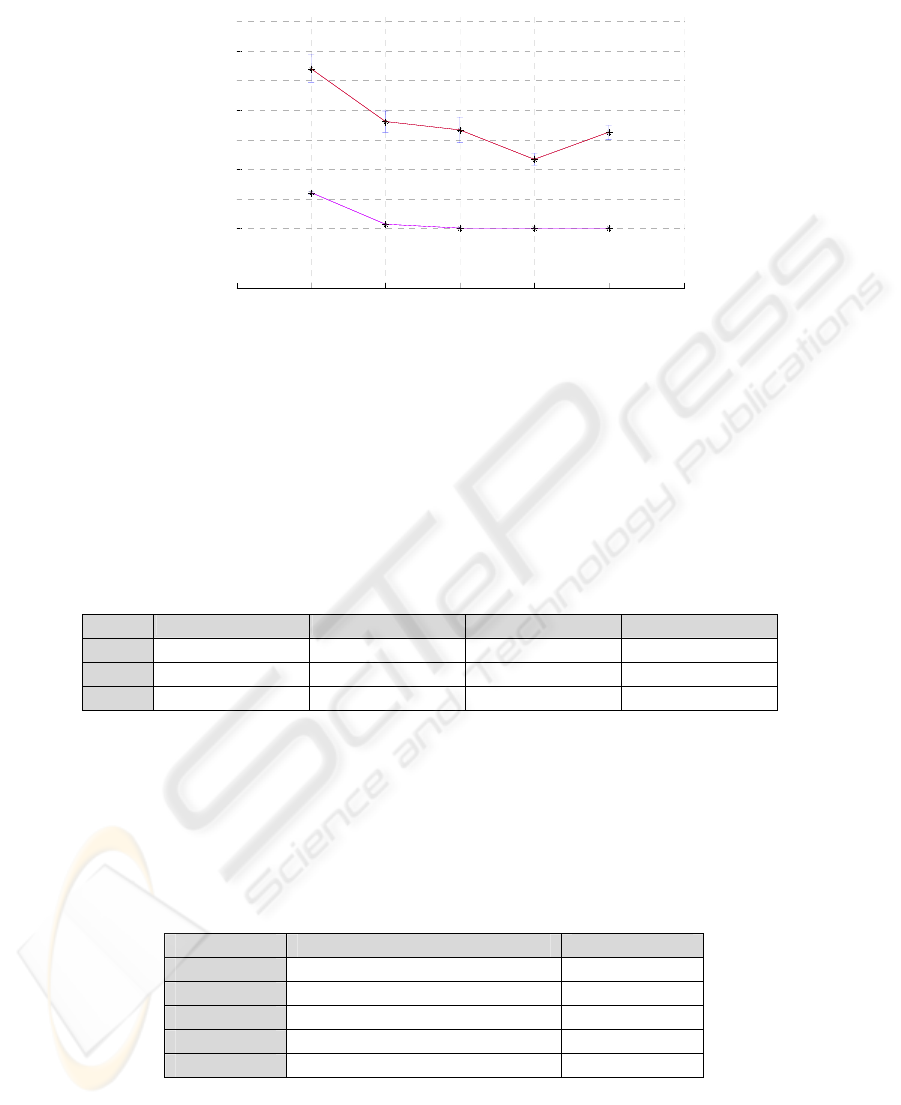
For estimation of the optimal segment length, we empirically tested several lengths

from 5 to 25 seconds with steps of 5 seconds. A length of 20 seconds showed the best

results, leading to 5 times of the amount of data in contrast to the raw data (figure °2).

In order to estimate the best frequency bands for spectral domain feature extraction

methods, we empirically tested various lower (0-50 sec-1) and upper (10-500 sec-1)

cut-off frequencies and step sizes (0.5-30 sec-1).

0 10 20 30

error [%]

mentlän

[

sec

]

ment len

[

sec

]

error [%]

Fig. 2. Estimation of the best segment length. Raw data was sequentially segmented in lengths

from five to 25 (five steps) seconds. For each length, 00 vs. 10 was tested using OLVQ as

classification method. Red line shows the test error, purple line train error. Best results at

segment length of 20 seconds

Table 2 shows the results of the optimal frequency bands. The high values for f

are surprising, because based on statements in literature (e.g. [10], [13]) the maximal

frequency of body sway should be lower than 1 Hz. ∆f is very large as well, which

leads to a strong averaging of up to 560 PSD values (WOSA).

Table 2. Optimal upper and lower frequencies and step sizes that minimized test error. Values

were empirical estimated using 00 vs. 10 and classification method OLVQ

Periodogram WOSA BURG MTM

0,9 0,6 50,0 0,7

350,0 500,0 500,0 500,0

∆f

9,50 28,0 10,0 13,0

A model order of 46 minimized the error at the Burg method best; in addition, the

time-bandwidth product of MTM showed best results at a value of 8. Burg’s model

order generally showed saturation at a value of 30 and only small improvements of

less than 4% error.

Table 3. Five best results of time domain features, extracted from the 200 best feature

combinations. Feature set enumeration shows the occurrence of single features in the

combination. They show a high variability, which makes a judgment of every single feature

impossible

ranking feature set E

TEST

[%]

1 4 7 12 13 14 26,2

2 1 2 3 8 16 17 18 27,1

3 1 5 7 8 13 14 27,3

4 4 7 12 14 23 27,6

5 3 4 5 6 8 12 15 16 18 21 22 28,2

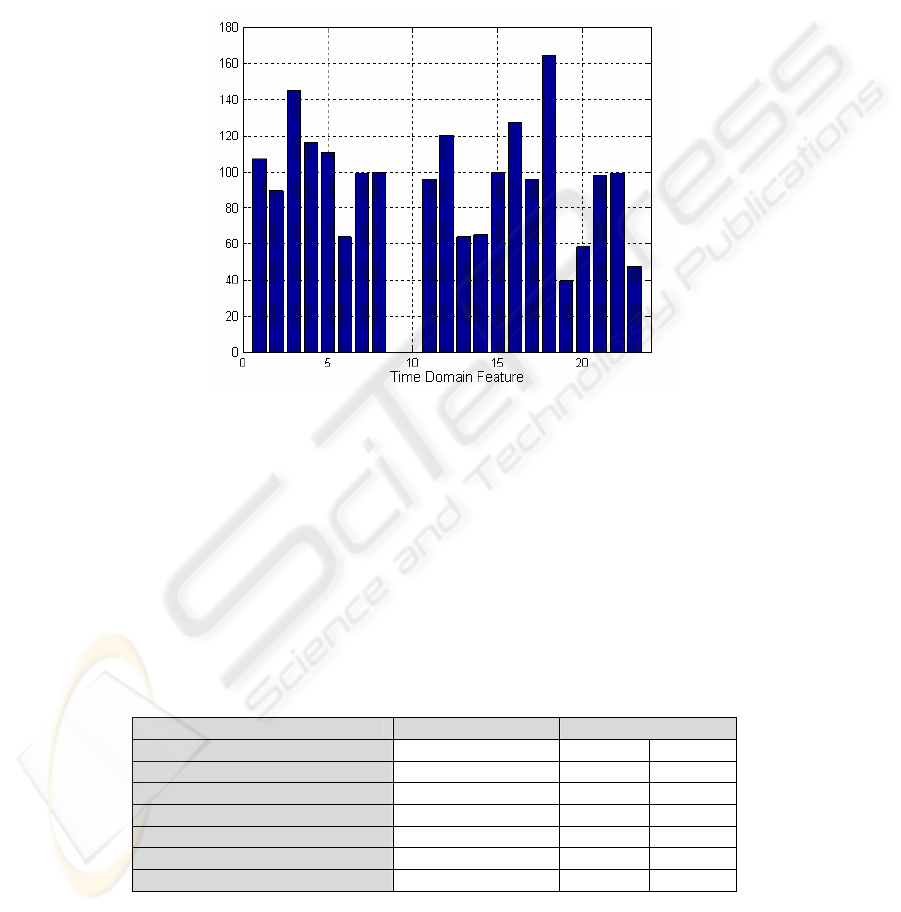
To estimate the best combinations of time domain features plus total spectral

energy, test errors of all 2²³ combinations were calculated. The distribution frequency

of the features in the 200 combinations with the best classification results was

calculated and plotted on a histogram (figure °3). Additionally, the five best

combinations are shown in table °3. The results point out a high variability of features

in these combinations, which makes a judgment of every single feature impossible.

Just the low frequency of features involved in the 200 feature combinations with

minimal test error (figure °3) leads to the worse classification ability of some features.

Fig. 3. Absolute frequency of 200 best feature numbers. From all 2²³ feature combinations 200

with the lowest test error were extracted to estimate the classifiability of each single feature. A

high frequency of a feature means good classifiability

The best five combinations of time domain feature extraction methods and the best

two from the spectral domain, namely MTM and Burg, were than used to examine the

optimal classification method. At all classification methods, we empirically estimated

the number of neurons to minimize the estimation error.

Table 4. Results of the comparison of classification methods (TDX = x-th combination of time

domain feature extraction methods). Results point out two classification methods to be suitable:

For spectral domain OLVQ, for time domain GCS. Results of GCS show a very high variance

and a much higher test error at all

feature extraction method class. method E

TEST

[%]

Burg OLVQ 2,2 ± 0,0

MTM OLVQ 8,0 ± 0,5

TD1 GCS 16,7 ± 4,5

TD2 GCS 29,8 ± 10,8

TD3 GCS 23,7 ± 6,6

TD4 GCS 23,8 ± 8,6

TD5 GCS 20,8 ± 6,3

Analysis of the results pointed out that two methods seem to be suitable. For

spectral domain it was OLVQ, for time domain GCS (table °4). For computing the

remaining combinations of the study, just the Burg Method for feature extraction and

OLVQ for classifying were used, because all other methods showed a considerably

higher test error.

3.2 Evaluation of the study

All trials were binary tested against each other, so the neural networks had to solve

two-class problems with an a priory test error of 50%. Our assumption was, that the

different trial modalities are, the better classification results (low test error) would be.

For instance, 00 vs. 11 and 00 vs. 12 should be good classifiable because every

modality differs, 11 vs. 12 should be the opposite, because the modalities here are

rather the same.

Table °5 gives an overview over the results. In opposition to our assumption, 00 vs.

10 showed the lowest test error. All other results accord with it, but the great

difference between combination 2 and 3 seems to be inexplicable, because the

modalities between both combinations differed only in length of the binaural

stimulation, plus all subjects reported equal feelings. However, the results of 11 vs. 12

confirm our assumption once more, leading to high test errors when modalities equal

Table 5. Results of study. For each classified trial the optimal number of neurons is given,

estimated empirically. The custom “eyes open vs. eyes closed” combination showed best

results, against our expectation that 00 vs. 11 or 00 vs. 12 would do this

classified trials # neurons E

TEST

[%]

00 vs. 10 95 4,2 ± 1,8

00 vs. 11 22 9,6 ± 2,0

00 vs. 12 60 16,2 ± 2,9

10 vs. 11 55 17,3 ± 2,7

10 vs. 12 97 20,2 ± 3,1

11 vs. 12 97 23,8 ± 2,8

4 Conclusion

Postural sway of nine healthy volunteers was measured in four trials with different

modalities of visual feedback and binaural stimulation. Raw data was segmented in

order to multiply data for the classification methods and beware stationarity of the

signal. 15 different feature extraction methods of time and spectral domain were

applied than to the segmented data. Parameters of these methods, including feature

combination in time and frequency band in spectral domain, were optimized by

minimizing the empirical error. The best combinations of time domain feature

extraction methods and the best from the spectral domain were than used to examine

the optimal classification method. It turned out, that Burg autoregressive method of

power spectral density estimation and Optimized Learning Vector Quantization was

the best method combination. The classification task “no impairment” versus “visual

impairment”, i.e. “eyes open” versus “eyes closed”, showed best discriminative

performance indicated by mean test errors of 4.2%.

In comparison to spectral domain, time domain features showed an unexpectable

low performance, for which we have no explanation. In our opinion technical

limitations play no role, in addition our system is technically improved, with a

exceptionally high sampling rate of 1000 sec

-1

and a 14 bit resolution in AD

converter. Also the task duration of 100 sec is higher in comparison to other authors,

the utilized classification algorithms are very adaptive and are much more sensitive

than every group oriented statistic. It is astonishing that spectral features perform so

much better than time domain features. Mean test errors of 4.2% are an extraordinary

performance in the domain of stochastic biosignals. The pilot study pointed out, that

the established biosignal analysis system gained a high sensitivity on small postural

influences. Future work should be oriented on investigation on more subjects and

more repetitive measurements over several weeks.

References

1. Chiari, L., Rocchi, L. and Cappello, A.: Stabilometric parameters are affected by

anthropometry and foot placement. Clinical Biomechanics (2002) 666-677

2. Clair, K.L. and Riach, C.: Postural stability measures: what to measure and for how long.

Clinical Biomechanics (1996) 176-178

3. Collins, J.J. and De Luca, C.J.: Upright, correlated random walks: A statistical-

biomechanics approach to the human postural control system. Chaos (1995) 57-63

4. Fransson, P.A. et al.: Adaption to vibratatory perturbations in postural control. IEEE

engineering in medicine and biology Magazine (2003) 53-57

5. Fritzke, B.: Vektorbasierte Neuronale Netze. Universität Erlangen - Nürnberg (1998)

6. Harris, C.S.: Effects of increasing intensity levels of intermitted and continuous 1000 Hz

tones on human equilibrium. Perceptual and Motor skills (1972) 395-405

7. Joachims, T.: Learning to classify text using support vector machines.

KluwerAc.Pub.(2002)

8. Kohonen, T.: Learning Vector Quantization. Neural Networks (1988) 303-306

9. Kohonen, T.: Self organizing maps. Berlin, Heidelberg, New York: Springer Verlag (2001)

10. Loughlin, P.J. and Redfern, M.S.: Spectral characteristics if visually induced postural sway

in healthy elderly and healthy young subjects. IEEE Trans.Neur.Sys. (2001) 24-30

11. Loughlin, P. and Redfern, M.: Analysis and modelling of human postural control. IEEE

Engineering in Medicine and Biology Magazine (2003) 18

12. Nakagawa, H. et al.: The contribution of proprioception to posture control in normal

subjects. Acta Otolaryngol (1993) 112-116

13. Oie, K.S. et al. Multisensory fusion: simultaneous re-weighting of vision and touch for the

control of human posture. Cognitive Brain Research (2002) 164-176

14. Oostervelt, W.J., Polman, A.R. and Schoonheyt, J.: Vestibular implications of noise-inducd

hearing loss. British Journal of Audiology (1982) 227-232

15. Percival, D.B. et al. : Spectral analysis for physical applications. Cambridge University

Press (1993)

16. Raper, S.A. and Soames, R.W.: The influence of moving auditory fields on postural sway

behaviour in man. European Journal of Applied Physiology (1992) 241-245.

17. Sakellari, V. and Soames, R.W.: Auditory and visual interactions in postural stabilization.

Ergonomics (1996) 634-648

18. Vapnik, V.: Statistical Learning Theory. Chichester, GB: Wiley (1998)