A Randomized Gathering Algorithm for Multiple

Robots with Limited Sensing Capabilities

⋆

Noam Gordon, Israel A. Wagner and Alfred M. Bruckstein

Center for Intelligent Systems, CS Department

Technion — Israel Institute of Technology

Haifa 32000, Israel

Abstract. Consider a swarm of weak, anonymousandhomogeneousrobotslack-

ing memory, orientation, and communication capabilities, and having myopic

sensors that tell them the directions to nearby robots, but not the distance from

them. We present a simple randomized algorithm which, when performed by all

members of the swarm, gathers them in a small region. We explore the interesting

global phenomena that occur during the process, evident from our analysis and

simulations.

1 Introduction

In this paper, we present a very simple algorithm that makes a swarm of very simple

robots perform a seemingly simple task — getting together in a small region. From a

practical standpoint, it can be useful for collecting multiple ant-robots after they have

performed a task in the ﬁeld; for enabling them to start a mission, after being initially

dispersed (e.g., parachuted); or for aggregating many nano-robots in a self-assembly

task. From a theoretical standpoint, it is the most basic instance of the formation prob-

lem, i.e., the problem of arranging multiple robots in a certain spatial conﬁguration.

While advanced intelligent robots are certainly capable of gathering, the problem is

most challenging when the robots are ant-like or less — having very limited abilities,

e.g., myopic, disoriented and lacking explicit communication capabilities.

Several theoretical works on this subject exist. Current approaches include agree-

ment on a meeting point with some unique geometrical property [1–4]; using a common

compass [5]; cyclic pursuit [6–8]; and others [9–11]. Sugihara et al. suggested a simple

way to ﬁll a convex shape, which is also useful for gathering [12].

These methods rely on strong assumptions about the robots (or agents as we shall

call them henceforth): Some rely on labeling (e.g., pursuit), some on common orienta-

tion, and many on inﬁnite-range visibility. Nearly all works rely on the agents’ ability

to measure their mutual distances.

In this work, we suggest a simple gathering algorithm, which relies on very few

capabilities: Our agents are anonymous, homogenous, memoryless, asynchronous, my-

opic and are incapable of measuring mutual distances. We are not aware of previous

works using this limited model. The inspiration and motivation for this work came from

⋆

This research was partly supported by the Ministry of Science Infrastructural Grant No. 3-942.

Gordon N., A. Wagner I. and M. Bruckstein A. (2005).

A Randomized Gathering Algorithm for Multiple Robots with Limited Sensing Capabilities.

In Proceedings of the 1st International Workshop on Multi-Agent Robotic Systems, pages 56-63

DOI: 10.5220/0001194500560063

 SciTePress

experiments with real robots in our lab [13], made from LEGO parts and very crude

sensors, which are range-limited and do not provide usable distance measurements.

In [14], we presented a simple deterministic gathering algorithm, which is similar

in idea to the aforementioned polygon-ﬁlling algorithm of Sugihara et al., yet it has

the additional property of maintaining mutual visibility between the robots, in order to

cope with their shortsightedness. In this work, we present a randomized variant of the

algorithm. Due to space restrictions, we omitted the proofs and abridged the discussion.

More details can be found in [14] and in an upcoming extended paper.

2 Model and Algorithm

We begin with a deﬁnition of the world model. Then, we discuss the conditions which

guarantee that visibility is maintained between our myopic agents, and present the pro-

posed algorithm.

2.1 Model

The world consists of the inﬁnite plane IR

and n point agents living in it. We adapt

Suzuki and Yamashita’s convenient way of modeling a system of asynchronous agents

[4]: Time is a discrete series of time steps t = 0, 1, . . .. In each time step, each agent

may be either awake or asleep, having no control over the random scheduling of its

waking times. A waking agent senses its environment, and is able to move instantly to

any point within a distance σ (the maximum step length). The agent is able to see other

agents within distance V (the visibility radius or range). However, it cannot measure its

distance from them. It only knows the directions in which the nearby agents are found,

i.e., the input is a cyclic list of angles θ

, . . . θ

(relative to some arbitrary direction,

e.g., the agent’s heading). There are no collisions. Several agents may occupy the same

point.

All agents are memoryless, anonymous (indistinguishable in their appearance)

and homogenous (they lack any individuality or identity, and perform the same algo-

rithm).

Regarding the agents’ activity schedule, we only assume that the agents are strongly

asynchronous: For any subset G of the agents and in each time step, the probability that

G will be the set of waking agents is bounded from below by some constant ε > 0.

Deﬁne the mutual visibility graph as an undirected graph with n vertices, represent-

ing the agents, and an edge between each pair of agents, if and only if they can see each

other, i.e., the distance between them is at most V .

2.2 Maintaining Visibility

We now present a sufﬁcient condition, on any algorithm, for maintaining mutual visi-

bility between agents. In what follows, denote a disc of radius r and center a (where a

may signify the location of an agent a) by B

(a). Also, denote

µ ≡ min (V/2, σ) .

In this case, they have undeﬁned relative directions and simply ignore each other.

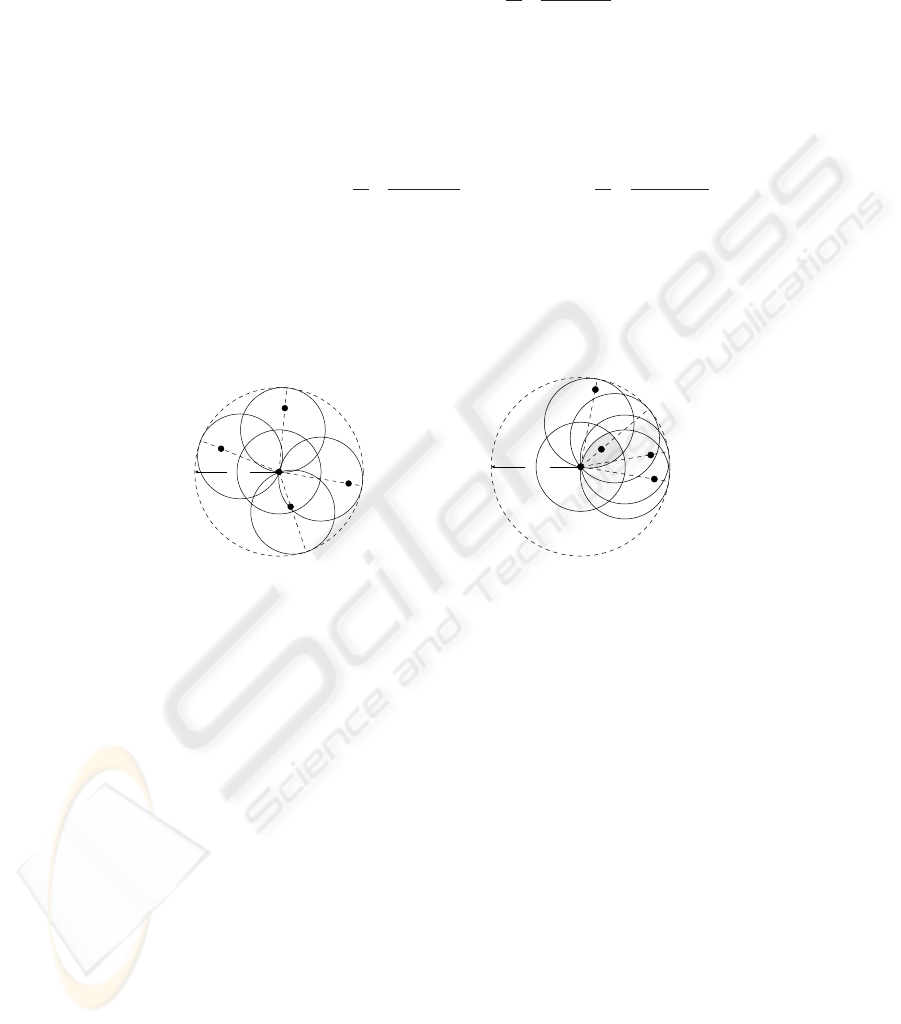
Let agent a see m agents b

, . . . b

, and deﬁne the allowable region AR(a) of a:

AR(a) ≡ B

(a) ∩

i=1

V/2



a +

− a

− ak



. (1)

It is easily seen (cf. Fig. 1) that AR(a) is not empty if and only if all visible agents are

contained within a sector or “wedge” of less than half the disc B

(a), i.e., its angle is

less than π. In this case, AR(a) is simply the intersection of B

(a) and the two discs

corresponding to the agents on the wedge’s bounds (e.g., b

and b

in Fig. 1(b)):

AR(a) = B

(a) ∩B

V/2



a +

− a

− ak



∩B

V/2



a +

− a

− ak



. (2)

Also, if m = 0, then AR(a) = B

(a). The following lemma holds.

Lemma 1. If each agent conﬁnes its movements to the allowable region deﬁned above,

then existing visibility will be maintained.

(a)

(b)

Fig.1. Maintaining visibility. (a) a is surrounded and cannot move (AR(a) = ∅). (b) a can move

only within the shaded area.

2.3 The Algorithm

The proposed algorithm is as follows:

Move to a uniformly-distributed random point in the allowable region (unless

it is empty, in which case do not move).

Interestingly, the algorithm doesn’t seem to “care” for anything but maintaining

visibility, yet its rationale is similar to that of the deterministic algorithm from [14]

(where the agent moves as far as allowed along the bisector of the wedge): The agents

inside the area occupied by the swarm do not move, while the agents at the outskirts

move inside, making the swarm shrink, until all agents are gathered densely in a small

cluster.

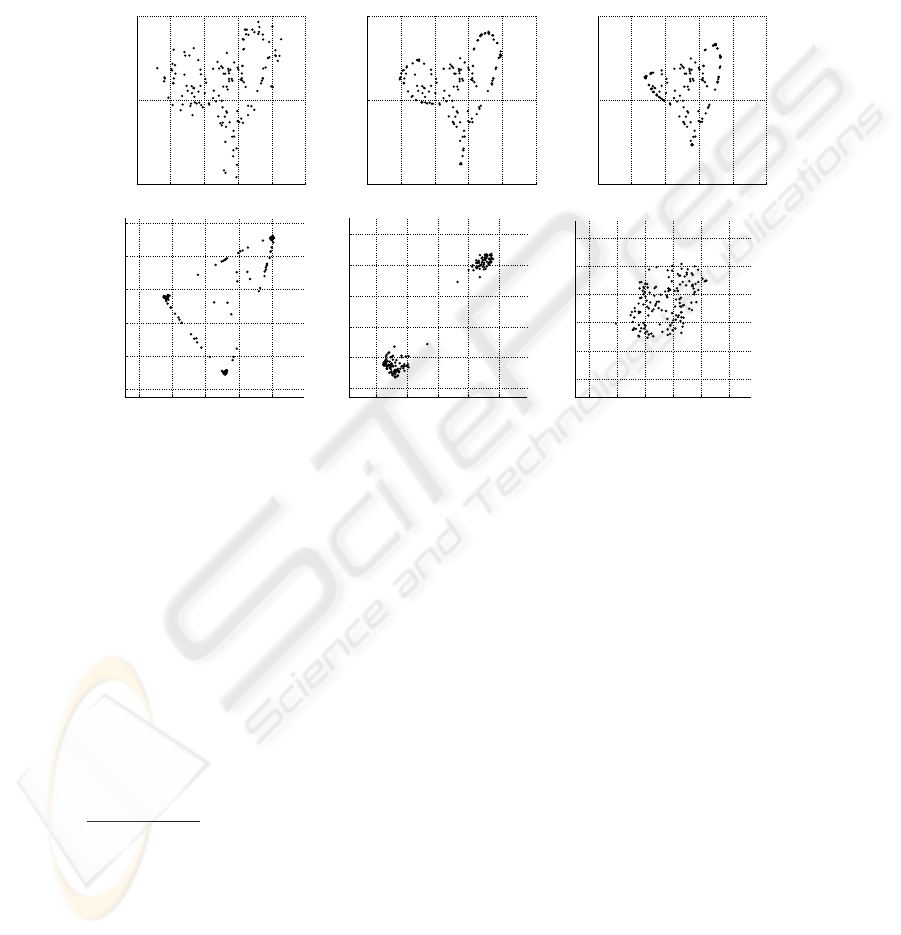
3 Results and Analysis

Despite its extreme simplicity, the algorithm effectively manages to gather all agents in

a small cluster. Moreover, we observed in our simulations some very interesting global

phenomena, which we discuss in this section.

−20 0 20 40 60 80

−50

t = 0

−20 0 20 40 60 80

−50

t = 40

−20 0 20 40 60 80

−50

t = 150

20 25 30 35 40

−5

t = 800

31 32 33 34 35

t = 1300

32.2 32.4 32.6 32.8 33 33.2

8.6

8.8

9.2

9.4

9.6

t = 1500

Fig.2. A typical run. Here n = 150, σ = 1, V = 10, and each agent wakes up in each time step

with probability p = 0.6. Note that the scale changes between frames.

3.1 Global Behavior

The qualitative behavior of the algorithm is clearly divided into two phases (similarly

to the deterministic variant). First, in the contraction phase, the area occupied by the

agents contracts into a small dense cluster

. In a large swarm, the contraction process

exhibits an interesting behavior, where the occupied area shrinks non-uniformly, as-

suming an approximate polygonal shape with a few corners and roughly straight edges

between them (cf. Fig. 2). The corners are actually dense clusters of several agents. The

edges are “belts”, containing the agents that were swept by the contracting boundary.

The density of agents along the edges is much lower than in the corners. More gener-

ally, there is a correlation between high curvature (of the boundary) and high density

We use the term “area occupied by the agents” freely, as a subjective observation of the agents’

distribution or the shape of the swarm. It can be deﬁned formally as the area enclosed by

laying line segments between all pairs of mutually visible agents. When all agents are mutually

visible, this area equals the convex hull of the agents’ locations. An alpha-shape may also be

considered, however its parameter α has no clear meaning in our problem.

of agents. We believe that there is a positive-feedback relationship between density and

curvature, which results in the large-scale polygonal shape, having sharp dense corners

and linear edges of lower density.

The occupied area contracts until it becomes a small dense cluster with a mean

diameter

of about µ. At this stage, the wandering phase begins. The dense cluster

stops contracting, and begins wandering in the plane, instead. The reason to this change

is clear: The agents’ step sizes are not affected by the scale of the occupied area. As

long as the area is large in comparison to µ, the agents on its boundary generally move

inside it, making it contract. However, once the area becomes smaller, the agents’ steps

become relatively larger, so they leap over it, instead. As a result of these leaps, the

cluster drifts along the plane indeﬁnitely. Note that since there is full visibility between

the agents at this stage, only the agents at the vertices of the convex hull are able to

move.

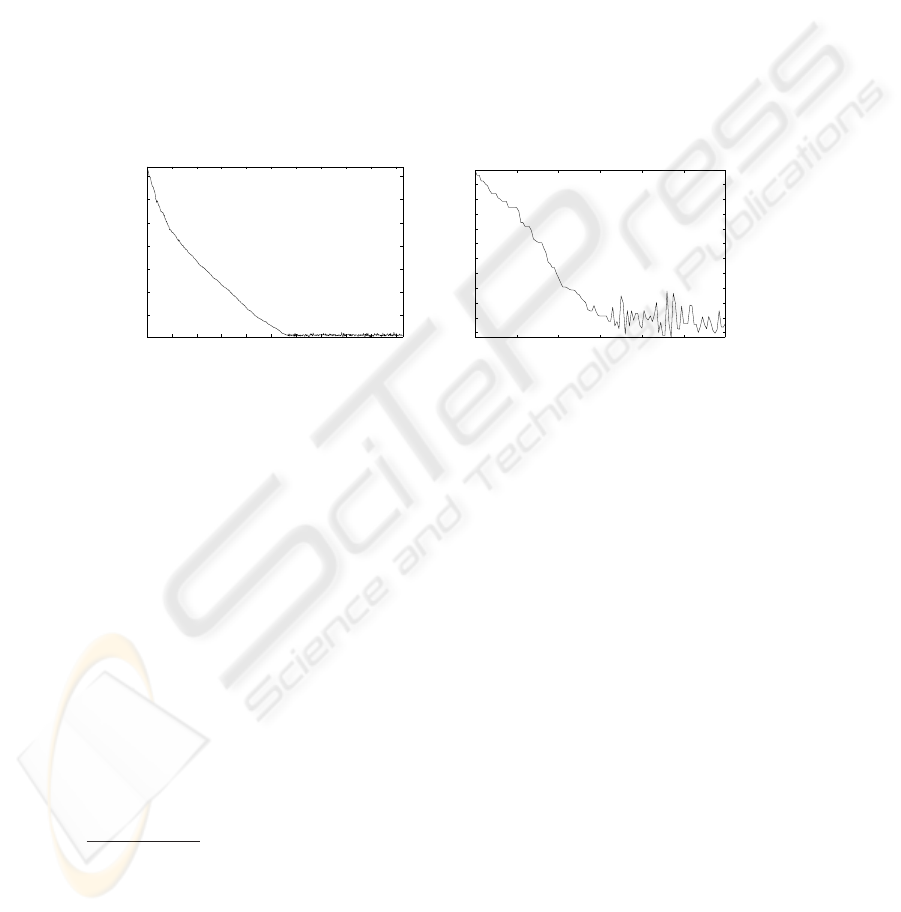
100 200 300 400 500 600 700 800 900 1000

time

diameter

(a)

500 520 540 560 580 600 620

0.6

0.8

1.2

1.4

1.6

1.8

2.2

2.4

2.6

time

diameter

(b)

Fig.3. The diameter in a typical run of the algorithm. Here n = 60, σ = 1, V = 5, and p = 0.6.

(a) The phase transition is very clear. (b) Zooming in on the transition moment. Note that the

mean diameter is about 0.8µ after the transition.

When n ≤ 2, the two algorithm variants act differently. In the deterministic algo-

rithm, a single agent will not move, and a pair will always remain on one line. In the

randomized variant, the agents will roam the plane in either case.

3.2 Guaranteed Convergence

The following theorem holds (We omitted the proof for space considerations).

Theorem 2. Given an initial conﬁguration with a connected visibility graph, the agents

will gather and forever remain in a cluster whose diameter is bounded by V , in ﬁnite

expected time.

The proof idea is as follows: We show that, in every time step, there exists an agent

(speciﬁcally, one located at a vertex of the convex hull), which has a strictly positive

The term mean diameter here refers to the average diameter over time (in a given run), not

probability space.

i.e., positive and bounded away from zero by some constant.

chance of moving inside the convex hull and closer to the center of mass (average of the

agents’ positions) by a strictly positive amount, if it is the only agent which wakes up.

By our strong asynchronicity assumption, the chance that this will happen is also strictly

positive (bounded by ε). This, in turn, will make the variance (sum of squared distances

from the center of mass) decrease by a strictly positive amount. Thus, with time, the

variance will decrease arbitrarily with probability 1. As the variance gets smaller, the

diameter must too, so at some point, the diameter will be V or less, which implies that

the visibility graph is a clique. By Lemma 1, it will remain a clique, and therefore the

diameter will remain bounded by V .

3.3 Evaluation of the Mean Cluster Diameter

Theorem 2 guarantees gathering to diameter V . However, the simulations clearly show

further contraction to a mean diameter of about 0.8µ during the wandering phase

, fairly

indifferently to the choice of n. With the deterministic algorithm, the mean diameter

typically settles at about 1.04µ.

When the agents are scattered (i.e., the diameter is much larger than µ) the diameter

is much more likely to decrease, and when the agents are gathered in a small cluster, it is

likelier to increase (e.g., consider a limit case of an inﬁnitesimally small cluster). Thus,

we infer that there exists a probabilistically stable equilibrium point for the diameter.

This point is the expected mean diameter.

An exact calculation of the expected mean diameter seems to be difﬁcult, yet the

following rough estimate for large n provides a surprisingly good prediction of the

measured results. Given a dense cluster P with diameter D(P ) ≪ V , we ﬁrst approxi-

mate its convex hull shape as a disc of diameter D(P ). The corner agents reside on its

boundary, with their wedge bisectors pointing to its center. We assume that σ ≪ V and

n is large, so that the allowable region of each corner agent is approximately a narrow

sector (i.e., a “pizza slice”) of a disc of radius µ. Now, we approximate the expected

mean diameter as that for which, for each corner agent, the probability of moving into

the convex hull equals the probability of leaping over it. Geometrically, it means that

the intersection of the narrow sector and the disc should contain half of the sector’s area.

This holds when the disc’s diameter is about µ/

√

2, which is quite close to the observed

typical mean diameter of 0.8µ.

In the deterministic variant of the algorithm, assuming that σ is small enough, the

agent simply moves a step of size µ on the bisector (i.e., along the disc’s diameter in our

approximation). Thus, the expected mean diameter is simply µ. Again, it agrees well

with the measured typical mean diameter of 1.04µ.

3.4 Composite Random Walking

The random wandering of the cluster is composed of the movements of the individual

agents in it (hence we term it a composite random walk). An interesting question is

Although we determined the moment of phase transition subjectively, it is evident from Fig. 3

that this moment is very clear. We calculated the average diameter from about 20 time steps

ahead of that moment until the end of the simulation (several hundred steps later).

whether this random walk is recurrent or not. Based on our observations, we conjecture

that it is indeed. If so, then it has a very important implication: Theorem 2 guarantees

that a conﬁguration with a connected visibility graph will contract. Thus, in the general

case, each connected component will contract into an independent cluster. Now, if the

cluster’s random walks are recurrent, then they will all meet eventually and merge into

one cluster.

In order to be recurrent, a two-dimensional random walk needs to be unbiased.

Obviously, when observing a single time step, the random movement is not distributed

uniformly in all directions, as it depends on the exact shape of the convex hull. However,

when integrating over many time steps, one may show that the cluster’s displacement is

distributed uniformly in all directions.

A single isolated agent performs a uniform random walk by deﬁnition. For two

agents, observe that the probability distribution of the center of mass’s displacement

is always symmetric along the line passing through the two agents, and has a constant

shape up to its orientation in the plane. Thus, the change of orientation has a con-

stant and unbiased distribution (i.e., same for clockwise and counterclockwise changes).

Therefore, over time, the orientation will be distributed uniformly, and, accordingly, the

center of mass’s displacement distribution will approach uniformity as well.

For n > 2, unfortunately, we don’t have an easy proof. Even with only three agents,

the state-space becomes complex and hard to analyze. Again, we conjecture that the

composite random walk of three or more agents is indeed recurrent. This seems to be

the case from observing long runs of the simulations.

4 Conclusions

The main contribution of our work is that we consider the gathering problem with such

severe limits on the agents’ sensors (being both myopic and unable to measure dis-

tances), in addition to being anonymous and memoryless. The proposed algorithm is an

example of how deceptively simple individual behaviors can yield complex emergent

global behaviors of the swarm — two distinct phases of contraction and wandering,

where the swarm ﬁrst assumes an approximate polygonal shape and then collapses into

a dense cluster wandering in the plane.

If our conjecture regarding the recurrence of the composite random walk proves to

be true, then the algorithm is a very powerful one, gathering all agents together into a

dense cluster, regardless of their initial distribution. We ﬁnd it intriguing that it does

that even though it is seemingly unconnected to the gathering problem, as the agents

just move randomly while trying to maintain their visibility. One may view this as an

argument that gathering is the only global task that such a swarm of weak robots can

do, i.e., it is a sort of an “upper bound” on the swarm behavior capabilities.

Further work should provide tighter estimates of the convergence rate, and analyze

the effect of noise and error, both in sensing and movement, on the resulting global

behavior.

References

1. Cieliebak, M., Flocchini, P., Prencipe, G., Santoro, N.: Solving the robots gathering problem.

In: Proc. of ICALP 2003. (2003)

2. Gordon, N., Wagner, I.A., Bruckstein, A.M.: Discrete bee dance algorithms for pattern for-

mation on a grid. In: Proc. of IEEE Intl. Conf. on Intelligent Agent Technology (IAT03).

(2003) 545–549

3. Schlude, K.: From robotics to facility location: Contraction functions, weber point, convex

core. Technical Report 403, CS, ETHZ (2003)

4. Suzuki, I., Yamashita, M.: Distributed anonymous mobile robots: Formation of geometric

patterns. SIAM Journal on Computing 28 (1999) 1347–1363

5. Flocchini, P., Prencipe, G., Santoro, N., Widmayer, P.: Gathering of autonomous mobile

robots with limited visibility. In: Proc. of STACS 2001. (2001)

6. Bruckstein, A.M., Cohen, N., Efrat, A.: Ants, crickets and frogs in cyclic pursuit. Technical

Report CIS-9105, Technion – IIT (1991)

7. Bruckstein, A.M., Mallows, C.L., Wagner, I.A.: Probabilistic pursuits on the grid. American

Mathematical Monthly 104 (1997) 323–343

8. Marshall, J.A., Broucke, M.E., Francis, B.A.: A pursuit strategy for wheeled-vehicle forma-

tions. In: Proc. of CDC03. (2003) 2555–2560

9. Ando, H., Oasa, Y., Suzuki, I., Yamashita, M.: A distributed memoryless point convergence

algorithm for mobile robots with limited visibility. IEEE Trans. on Robotics and Automation

15 (1999) 818–828

10. Lin, Z., Broucke, M.E., Francis, B.A.: Local control strategies for groups of mobile au-

tonomous agents. IEEE Trans. on Automatic Control 49 (2004) 622–629

11. Melhuish, C.R., Holland, O., Hoddell, S.: Convoying: using chorusing to form travelling

groups of minimal agents. Robotics and Autonomous Systems 28 (1999) 207–216

12. Sugihara, K., Suzuki, I.: Distributed algorithms for formation of geometric patterns with

many mobile robots. Journal of Robotic Systems 13 (1996) 127–139

13. The Center of Intelligent Systems, Technion IIT web site:

http://www.cs.technion.ac.il/Labs/Isl/index.html.

14. Gordon, N., Wagner, I.A., Bruckstein, A.M.: Gathering multiple robotic a(ge)nts with limited

sensing capabilities. Lecture Notes in Computer Science 3172 (2004) 142–153