
Rigidity and Persistence of Three and Higher
Dimensional Formations
Julien M. Hendrickx
1
, Barıs¸ Fidan
2
, Changbin Yu
2
, Brian D. O. Anderson
2
and
Vincent D. Blondel
1
1
Department of Mathematical Engineering, Universit
´
e Catholique de Louvain,
Avenue Georges Lemaitre 4, B-1348 Louvain-la-Neuve, Belgium
2
National ICT Australia Ltd. and
Research School of Information Sciences & Engineering., the Australian National University,
216 Northbourne Ave., Canberra ACT 2601 Australia
Abstract. In this paper, we generalize the notion of persistence, which has been
originally introduced for two-dimensional formations, to ℜ
d
for d ≥ 3, seeking
to provide a theoretical framework for real world applications, which often are
in three-dimensional space as opposed to the plane. We verify that many of the
properties of rigid and/or persistent formations established in ℜ
2
are also valid for
higher dimensions. Analysing the closed subgraphs and directed paths in persis-
tent graphs, we derive some further properties of persistent formations. We also
provide an easily checkable necessary condition for persistence.
1 Introduction
Multi-agent systems have attracted considerable attention recently as witnessed by ex-
plosion of papers in the area (see for example [1–4]). Agents, abstracted as vertices
of graphs in this paper (following [5,6]), can be thought as any autonomous agents
including combat robots, underwater vehicles, unmanned aerial vehicles, and ground
vehicles.
Many control tasks for point-agent systems involve maintaining of the distance be-
tween nominated pairs of agents. For such tasks, a graph can naturally be used to depict
the control architecture as follows: To each agent corresponds a vertex, and for each
⋆ ⋆ ⋆
The work of Julien M. Hendrickx and Vincent D. Blondel is supported by the Belgian Pro-
gramme on Interuniversity Attraction Poles initiated by the Belgian Federal Science Policy
Office, and by the Concerted Research Action (ARC) “Large Graphs and Networks” of the
French Community of Belgium. The scientific responsibility rests with its authors. Julien M.
Hendrickx is a FNRS (Belgian Fund for Scientific Research) fellow.
†
The work of Barıs¸ Fidan, Changbin Yu, and Brian D.O. Anderson is supported by National ICT
Australia, which is funded by the Australian Government’s Department of Communications,
Information Technology and the Arts and the Australian Research Council through the Back-
ing Australia’s Ability Initiative. Changbin Yu is an Australia-Asia Scholar supported by the
Australian Government’s Department of Education, Science and Training through Endeavours
Programs.
M. Hendrickx J., Fidan B., Yu C., D. O. Anderson B. and D. Blondel V. (2005).
Rigidity and Persistence of Three and Higher Dimensional Formations.
In Proceedings of the 1st International Workshop on Multi-Agent Robotic Systems, pages 39-46
DOI: 10.5220/0001193600390046
Copyright
c
SciTePress

agent (vertex) pair i, j there is a directed edge
−−→
(i, j) from i to j if i has a constraint on
the distance it must actively maintain from j.
In the recent control literature, the characterization of a system of the above type has
started to be attempted using the notion of rigidity of a directed graph [1, 5], which is
called persistence of a directed graph [6] as well. In this paper, we prefer to use the term
persistence in order to distinguish it from the undirected notion of rigidity. In Section
2, formal definition of persistence given in [6] is generalized to ℜ
d
for d ≥ 3, seeking
to provide a theoretical framework for real world applications, which often are in 3-
dimensional space as opposed to the plane. This definition has the following intuitive
meaning: a graph is persistent if, provided that all the agents are trying to satisfy their
distance constraints, the global structure of the formation is preserved, i.e. when the
formation moves, it necessarily moves as a cohesive whole. We will see that rigidity
of the underlying undirected graph is a necessary but not sufficient condition. This
will lead us to the notion of constraint consistence of graph, which is the additional
condition for a rigid graph to be persistent. Intuitively, a graph is constraint consistent
if every agent is able to satisfy all its distance constraints provided that all the others
are trying to do so. We will then show that a graph is persistent if and only if it is rigid
and constraint consistent.
In Section 3, we generalize some of the main properties of persistent graphs to 3-
or high dimensional graphs, drawing on established results in ℜ
2
.
In Section 4, we reason about the persistence of closed subgraphs of persistent
graphs and use this reasoning to analyze the directed paths in persistent graphs. As
results of this analysis, we present some further properties of persistent graphs and an
easily checkable necessary condition for persistence.
The paper is ended with the concluding remarks in Section 5. Note that all the
proofs in the paper are omitted because of space limitations. However, a full version
of this work together with the companion paper [7] is available in preprint from the
authors.
2 Rigidity and Persistence
In [6], rigidity, persistence, and some other related notions have been defined for di-
rected graphs in ℜ
2
. In this section, we generalize these definitions to be applicable
for any space ℜ
d
, d ∈ {1, 2, 3, . . .}. Some of the terms we use such as “rigidity” are
undirected notions, i.e., notions that are defined for undirected graphs. These notions,
however, apply to directed graphs as well, e.g., we call a directed graph rigid iff its un-
derlying undirected graph is rigid. Note that, in directed graphs, rigidity and the other
undirected notions are not affected by modification of the edge directions.
In ℜ
d
(d ∈ {1, 2, 3, . . .}), a representation of an undirected graph G = (V, E) with
vector set V and edge set E is a function p : V → ℜ
d
. We say that p(i) ∈ ℜ
d
is the
position of the vertex i, and define the distance between two representations p
1
and p
2
of the same graph by
d(p
1
, p
2
) = max
i∈V
||p
1
(i) − p
2
(i)|| .

A distance set
¯
d for G is a set of distances d
ij
> 0, defined for all edges (i, j) ∈ E.
A distance set is realizable if there exists a representation p of the graph for which
||p(i) − p(j)|| = d
ij
for all (i, j) ∈ E. Such a representation is then called a realiza-
tion. Note that each representation p of a graph induces a realizable distance set (defined
by d
ij
= ||p(i) − p(j)|| for all (i, j) ∈ E), of which it is a realization.
A representation p is rigid if there exists ǫ > 0 such that for all realizations p
′
of
the distance set induced by p and satisfying d(p, p
′
) < ǫ, there holds ||p
′
(i) − p
′
(j)|| =
||p(i) − p(j)|| for all i, j ∈ V . (We say in this case that p and p
′
are congruent). A
graph is said to be generically rigid if almost all its representations are rigid. Note that
the reasons for which we only require almost all representations to be rigid instead of
all of them will be detailed in Remark 1.
As mentioned above, rigidity is an undirected notion, and is therefore insufficient to
characterize persistence. As noted in [6], rigidity of a representation only means that if
an external observer (or some physical properties) makes sure that the distance between
the positions of any pair of vertices connected by an edge remains constant, then all the
sufficiently close realizations of the induced distance set are congruent to each other.
But, in a typical system of autonomous agents, there is no such external observer. Each
agent is only aware of its own distance constraints, and can “move freely” as long
as these particular constraints are satisfied. For example, agents that have only one
constraint can move along a hyper-sphere centered on the position of the only other
agent of which they are aware. So, it could happen that because one agent i is moving
on such a hyper-sphere, it becomes impossible for another agent j to satisfy all its
constraints, especially if j has d + 1 or more constraints. So, in order to have a more
formal definition of persistence, we first need to characterize the fact that each agent is
trying to keep the distances from its neighbors constant.
Let us thus fix a directed graph G = (V, E) depicting a point-agent system archi-
tecture, where each agent corresponds to a vertex in V , and for each agent (vertex) pair
i, j there is a directed edge
−−→
(i, j) ∈ E from i to j if i has a constraint on the distance
it must actively maintain from j. Let us also fix desired distances d
ij
> 0, ∀
−−→
(i, j) ∈ E
and a representation p. We say that the edge
−−→
(i, j) ∈ E is active if ||p(i) − p(j)|| = d
ij
.
We also say that the position of the vertex i ∈ V is fitting for the distance set
¯
d if it is
not possible to increase the set of active edges leaving i by modifying the position of
i while keeping the positions of the other vertices unchanged. More formally, given a
representation p, the position of vertex i is fitting if there is no p
∗
∈ ℜ
d
for which the
following strict inclusion holds:
{
−−→
(i, j) ∈ E : ||p(i) − p(j)|| = d
ij
} ⊂ {
−−→
(i, j) ∈ E : ||p
∗
− p(j)|| = d
ij
} (1)
This condition intuitively means that the agent i cannot satisfy additional distance con-
straints without breaking some that it already satisfies, as shown in the two-dimensional
example in Figure 2, which is drawn from [6]. A representation of a graph is a fitting
representation for a certain distance set
¯
d if all the vertices are at fitting positions for
¯
d.
Note that any realization is a fitting representation for its distance set.
We can now give a formal definition of persistence: A representation p is persistent
if there exists ǫ > 0 such that every representation p
′
fitting for the distance set induced
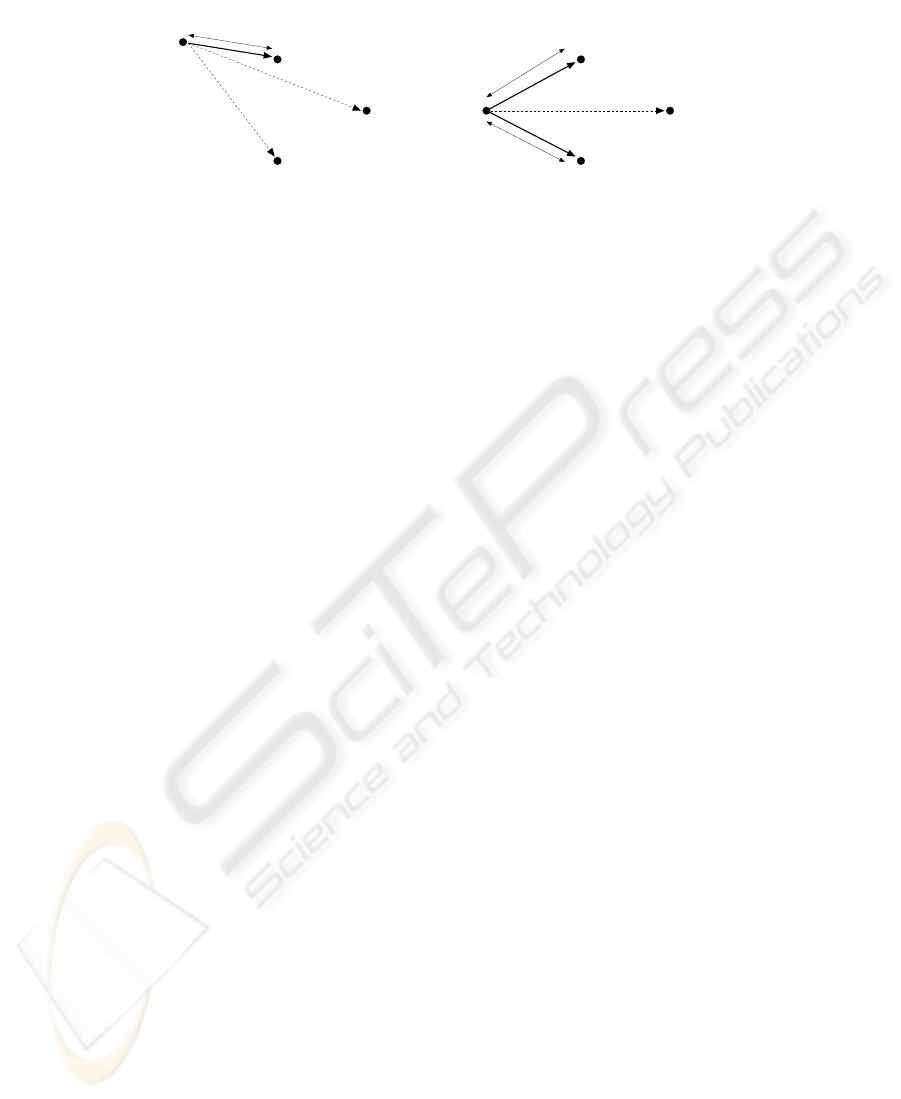
c
3
2
1
4
4
c
3
2
1
c
(a) (b)
Fig.1. Suppose that d
41
= d
42
= d
43
= c. The position of 4 in (a) is not fitting because it only
makes
−−−→
(4, 1) active while there exists a position that would make both
−−−→
(4, 1) and
−−−→
(4, 3) active. On
the other hand, its position in (b) is fitting because no point can be at the same time at a distance
c from 1, 2 and 3.
by p and satisfying d(p, p
′
) < ǫ is congruent to p. A graph is then generically persistent
if almost all its representations are persistent.
One can show that a generically persistent graph is always generically rigid. A suf-
ficient condition for a generically rigid graph to be generically persistence is the generic
constraint consistence. A representation p is constraint consistent if there exists ǫ > 0
such that any representation p
′
fitting for the distance set
¯
d induced by p and satisfying
d(p, p
′
) < ǫ is a realization of
¯
d. Intuitively, the constraint consistence of a representa-
tion means that if each agent tries to satisfy its distance constraints (i.e., is at a fitting
position), then all the distance constraints will be satisfied, or equivalently, no agent
will be in a situation where it cannot satisfy some constraint. The illustration of such a
situation in ℜ
2
can be found in [6]. Again, we say that a graph is generically constraint
consistent if almost all its representations are constraint consistent.
We have the following useful equivalences for directed graphs in any d-dimensional
space ℜ
d
(d ∈ {1, 2, 3, . . .}), which have already been established for ℜ
2
in [6].
Theorem 1 A representation in ℜ
d
(d ∈ {1, 2, 3, . . .}) is persistent iff it is rigid and
constraint consistent. A graph in ℜ
d
(d ∈ {1, 2, 3, . . .}) is generically persistent iff it is
generically rigid and generically constraint consistent.
Remark 1 In our definitions of generic rigidity, persistence and constraint consistence,
a graph has a generic property if almost all its representations have the property. Some
discussions on using “generic” and “almost all” can be found in [6,8]. One reason
for using these terms, in ℜ
d
(d ∈ {1, 2, 3, . . .}), is to avoid the problems arising from
having d+1 or more vertices lying on a d
1
-dimensional hyper-surface where d
1
≤ d−1.
In the sequel, we avoid the use of “generic”.
3 Characterization of Persistent Graphs
In this section, we examine the properties of persistent graphs in three and higher di-
mensions, and present the fundamental results related to persistence. These results are
comparable to the properties of two-dimensional persistent graphs presented in [6], and

hence the corresponding propositions and lemmas are given as generic ones that are
applicable to ℜ
2
as well.
We begin the characterization of persistent graphs by giving a lower bound on the
number of active edges, and a sufficient condition for a graph to be constraint consistent.
In the sequel, d
−
(i) and d
+
(i) designate respectively the in- and out-degree of the
vertex i.
Lemma 1 Let i be a vertex of a graph G = (V, E). For almost all representations
p of G, there exists ǫ > 0 such that in every representation p
′
∈ B(p, ǫ) (i.e., such
that d(p, p
′
) < ǫ) fitting for the distance set induced by p, the number of active edges
leaving i is at least min (d, d
+
(i)). Consequently, a graph in which all the vertices have
an out-degree smaller than or equal to d is always constraint consistent.
The next proposition which is the generalization of Propositions 1 and 2 in [6] for
any arbitrary dimension d ∈ {1, 2, 3, . . .}, allows us to delete edges in a persistent
(constraint consistent) graph and maintain persistence (constraint consistence).
Proposition 1 A persistent graph in ℜ
d
(d ∈ {1, 2, 3, . . .}) remains persistent after
deletion of any edge
−−→
(i, j) for which d
+
(i) ≥ d + 1. Similarly, a constraint consistent
graph in ℜ
d
(d ∈ {1, 2, 3, . . .}) remains constraint consistent after deletion of any edge
−−→
(i, j) for which d
+
(i) ≥ d + 1.
An interesting corollary of Proposition 1 concerns the total number of degrees of
freedom. The number of degrees of freedom (DOF count) of a vertex is the maximal
dimension, over all representations of the graph, of the set of possible fitting positions
for this vertex. For example, in ℜ
3
, the DOF counts of the vertices with zero, one, and
two out-degrees are respectively 3, 2, and 1; all the other vertices have zero DOF. The
following result provides a natural bound on the total DOF count, i.e., the sum of the
vertex DOF counts of a persistent graph.
Corollary 1 The total DOF count of a persistent graph in ℜ
d
(d ∈ {1, 2, 3, . . .}) can
at most be d(d + 1)/2.
Remark 2 There are d-dimensional persistent graphs having a total DOF count less
than d(d + 1)/2. Figure 2 shows a three-dimensional persistent graph each vertex of
which has 1-DOF. The total DOF count for this example is 5, i.e., less than 3(3 + 1)/2.
As stated in Proposition 1, a persistent graph remains persistent after deletion of any
edge
−−→
(i, j) for which d
+
(i) ≥ d + 1. After successive deletions, we can thus reach in
this way a persistent graph whose vertices all have an outgoing degree that is smaller
than or equal to d. In the next theorem, which is analogous to Theorem 3 in [6] stated
for ℜ
2
, we see that a graph is persistent if and only if all the graphs obtained in this way
are rigid. This criterion allows us to note that a graph obtained by adding an edge to a
persistent graph is not necessarily persistent, as shown on the example in Figure 3.
Theorem 2 A d-dimensional graph is persistent if and only if all those subgraphs are
rigid which are obtained by successively removing outgoing edges from vertices with
out-degree larger than d until all such vertices have an out-degree equal to d.
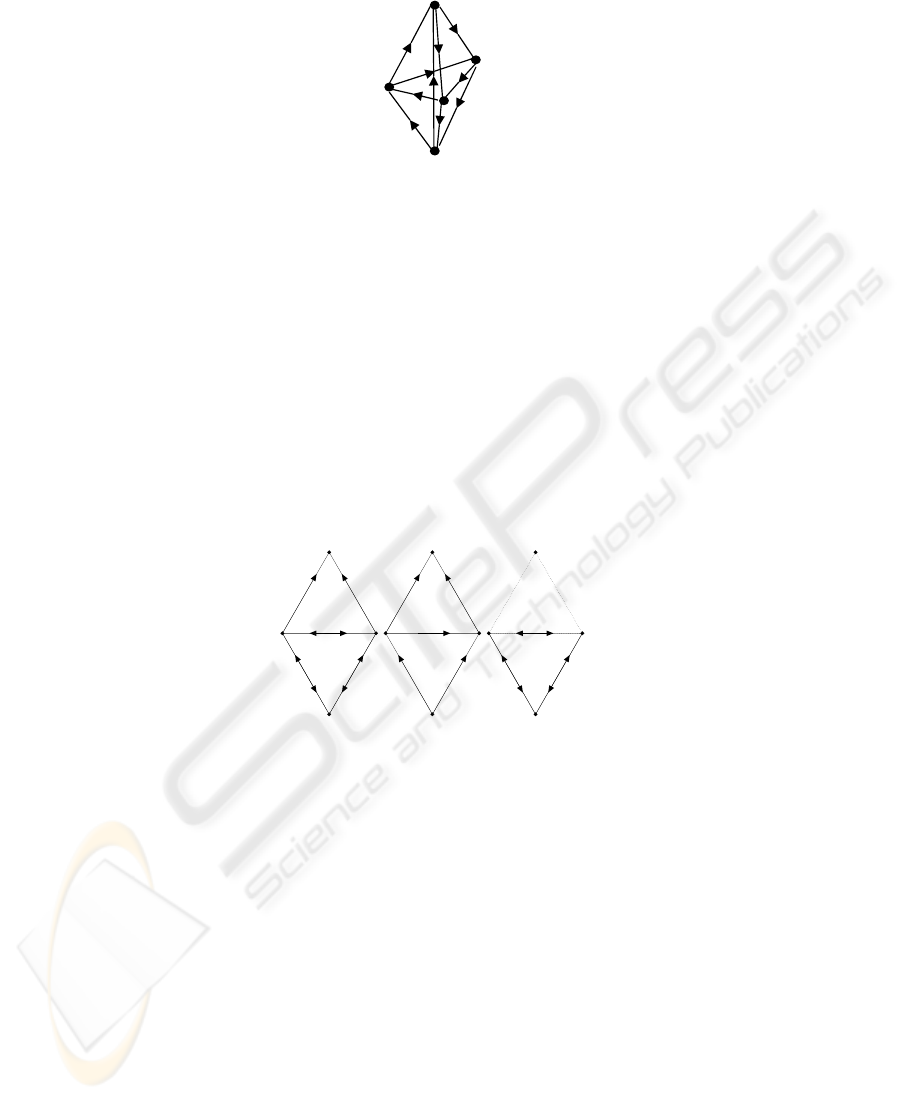
Fig.2. A persistent graph in ℜ
3
with all the vertices having out-degree 2 and hence 1-DOF.
Theorem 2 provides a non-polynomial time algorithm to check the persistence of
any d-dimensional graph for d ∈ {1, 2, 3, . . .}: It is sufficient to check the rigidity of all
subgraphs obtained by deleting the edges leaving vertices with out-degree larger than or
equal to d + 1 until all the vertices have an out-degree less or equal to d. An algorithm
with a smaller complexity would be useful in the case of large graphs, especially if there
is a high number of vertices with high out-degrees, but no such algorithm is currently
available. More discussions on determining the persistence of two-dimensional directed
graphs in polynomial time can be found in [6]. Moreover, [7] presents results leading
to a quadratic time algorithm for the case d = 3 for cycle-free graphs, which can be
generalized easily to any d ∈ {1, 2, 3, . . .}.
(a) (b) (c)
Fig.3. The two-dimensional graph represented in (a) can be obtained by adding an edge to the
persistent graph (b). However, by Theorem 2, it is not persistent because the subgraph represented
in (c) is not rigid. In the corresponding multi-agent system, this could arise from a combination
of unfortunate information architecture selections for the three agents of the cycle.
4 Closed Subgraphs and Directed Paths
In this section, we focus on the directed paths in persistent graphs and analyze some
related properties. As a part of this analysis, we reason about the persistence of closed
subgraphs of persistent graphs. An important outcome of our analysis will be an easily
checkable necessary condition (Proposition 3) for persistence. Note that the proofs of
many results concerning closed subgraphs rely on the properties of minimally persistent

graphs, i.e., persistent graphs for which no single edge can be removed without losing
persistence. These properties were omitted here due to space limitation, but a extended
studies of minimal persistence and its connections with the analogous notion of mini-
mal rigidity can be found in [6] or in the full version of this work, available in preprint
from the authors.
Consider a directed graph G = (V, E) in ℜ
d
(d ∈ {1, 2, 3, . . .}) and a subgraph
G
′
= (V
′
, E
′
) of G. G
′
is called a closed subgraph of G if for any vertex i ∈ V
′
,
−−→
(i, j) ∈ E implies j ∈ V
′
and
−−→
(i, j) ∈ E
′
. From the perspective of autonomous agent
formations, the agents corresponding to the vertices of V
′
are unaware of the existence
of those of V \ V
′
. We call then total DOF count of V
′
with respect to G the sum of
the DOF counts of all the vertices of V
′
. Using these notions, we reach the following
proposition.
Proposition 2 Let G = (V, E) be a persistent graph in ℜ
d
(d ∈ {1, 2, 3, . . .}) having
at least d vertices. If a vertex v ∈ V belongs to a closed subgraph of G containing
less than d vertices, the out-degree of v has to be smaller than or equal to d − 2. For
the set V
c
of all such vertices v, we have |V
c
| ≤ d − 1. On the other hand, any vertex
v
′
∈ V that does not belong to any closed subgraph of G having less than d vertices
is connected by a directed path (leaving v
′
) to all the vertices of G with positive DOF
count.
Remark 3 Given a directed graph G = (V, E) in ℜ
d
(d ∈ {1, 2, 3, . . . }), for any
vertex i ∈ V , there exists a certain closed subgraph of G containing i, which we call
the reachability subgraph of G for i. For a given i ∈ V , the reachability subgraph of
G for i can be formally defined as the subgraph G
′
= (V
′
, E
′
) of G where V
′
is the
set of all the vertices that can be reached from i (including the vertex i) by a directed
path in G and E
′
⊆ E is the set of all the edges e such that e joins a pair of vertices in
V
′
. It is easy to see that the reachability subgraph of G for the vertex i is the smallest
closed subgraph of G containing i, and equivalently, the intersection of all the closed
subgraphs of G containing i.
The following corollary, which immediately follows from Proposition 2, gives a
more explicit criterion to check the existence of a directed path between given two
vertices of a persistent graph in ℜ
3
, one of which has a positive DOF count.
Corollary 2 Let G = (V, E) be a persistent graph in ℜ
3
having at least 3 vertices. Any
vertex i is connected by a directed path (leaving i) to all the vertices of G with positive
DOF count unless one of the following holds:
1. i is a first leader, i.e., d
+
(i) = 0.
2. i is a first follower, i.e., d
+
(i) = 1 and there exists a j ∈ V such that
−−→
(i, j) ∈ E
and d
+
(j) = 0.
Using the above propositions about closed subgraphs and directed paths in persis-
tent graphs, we reach the following easily checkable necessary condition for persis-
tence. The detailed derivation of the criterion can be found in the full version of this
work, which is available in preprint from the authors.

Proposition 3 Let G = (V, E) be a persistent graph in ℜ
d
(d ∈ {1, 2, 3, . . .}) with at
least d vertices. Then all the closed subgraphs of G having more than d− 1 vertices are
persistent.
In ℜ
3
, Proposition 3 leads to the following corollary.
Corollary 3 Let G be a persistent graph in ℜ
3
with at least three vertices. Then any
closed subgraph G
′
of G is persistent unless G
′
consists of two disconnected vertices.
In other words, G has a non-persistent closed subgraph if and only if it contains two
vertices each having 3 DOFs.
5 Concluding Remarks
In this paper, we have generalized the notion of persistence given in [6] for 2-dimensional
directed graphs to dimensions higher than two, seeking to provide a theoretical frame-
work for real world applications, which often are in 3-dimensional space. We have veri-
fied that many of the properties already established for persistent graphs in ℜ
2
are valid
for higher dimensions as well. We have also analyzed the directed paths in persistent
graphs, exposed some further properties of such graphs in three or higher dimensions,
and given an easily checkable necessary condition (Proposition 3) for persistence. In
the companion paper [7], we analyze the “partial equilibrium problem”, a problem ob-
served in some persistent formations associated with feasibility of satisfying all the
constraints on all the agents simultaneously. We provide some criteria to check whether
a given persistent graph suffers from the partial equilibrium problem.
References
1. Baillieul, J., Suri, A.: Information patterns and hedging brockett’s theorem in controlling
vehicle formations. In: Proc. of the 42nd IEEE Conf. on Decision and Control. Volume 1.
(2003) 556–563
2. Ren, W., Beard, R.: A decentralized scheme for spacecraft formation flying via the virtual
structure approach. AIAA Journal of Gudiance, Control and Dyanmics 27 (2004) 73–82
3. Tanner, H., Pappas, G., Kumar, V.: Leader-to-formation stability. IEEE Transactions on Ro-
botics and Automation 20 (2004) 443–455
4. Eren, T., Anderson, B., Morse, A., Whiteley, W., Belhumeur, P.: Operations on rigid forma-
tions of autonoumous agents. Communications in Information and Systems (2004)
5. Eren, T., Whiteley, W., Anderson, B., Morse, A., Belhumeur, P.: Information structures to
secure control of rigid formations with leader-follower structure. (To appear)
6. Hendrickx, J., Anderson, B., Blondel, V., Delvenne, J.C.: Directed graphs for the analysis
of rigidity and persistence in autonomous agent systems. (2005) submitted to Int. J. Robust
Nonlinear Control.
7. Yu, C., Hendrickx, J., Fidan, B., Anderson, B.: Structural persistence of three-dimensional
autonomous formations. (1st International Workshop on Multi-Agent Robotic Systems–
MARS05’ as a companion of this paper)
8. Tay, T., Whiteley, W.: Generating isostatic frameworks. Structural Topology (1985) 21–69
